Beton - GZT
Das in der CSFM implementierte Betonmodell basiert auf den Werkstoffgesetzen für einachsigen Druck, die in DIN EN 1992-1-1 für die Bemessung von Querschnitten, die nur von der Druckfestigkeit abhängen, vorgeschrieben sind. Das in DIN EN 1992-1-1 (Abb. 26a) angegebene Parabel-Rechteck-Diagramm wird in der CSFM standardmäßig verwendet; Konstrukteure können jedoch auch ein vereinfachtes, elastisch ideal plastisches Verhältnis wählen (Abb. 26b). Wie es bei der Bemessung von klassischem Stahlbeton der Fall ist, wird die Zugfestigkeit vernachlässigt.
\[ \textsf{\textit{\footnotesize{Fig. 26\qquad The stress-strain diagrams of concrete for ULS: a) parabola-rectangle diagram; b) bilinear diagram.}}}\]
Unter Verwendung der Standardeinstellungen berücksichtigt die aktuelle Implementierung der CSFM in IDEA StatiCa Detail kein explizites Versagenskriterium in Bezug auf Dehnungen für Druckbeton (d.h. nach Erreichen der Spannungsspitze wird ein plastischer Zweig mit εcu2 (εcu3) mit einem Wert von 5% berücksichtigt, während DIN EN 1992-1-1 eine Grenzdehnung von weniger als 0,35% annimmt). Diese Vereinfachung macht die Überprüfung der Verformungskapazität von Strukturen, die bei Druck versagen, nicht möglich. Ihre finale Kapazität wird jedoch korrekt vorhergesagt, wenn zusätzlich zu dem in Abb. 2e definierten Faktor für gerissenen Beton (kc2, siehe Abb. 27)) die Zunahme der Sprödigkeit von Beton mit zunehmender Festigkeit anhand des in der fib Modellnorm 2010 definierten Reduktionsfaktors wie folgt berücksichtigt wird:
\[f_{cd}=\frac{f_{ck,red}}{γ_c} = \frac{k_c \cdot f_{ck}}{γ_c} = \frac{\eta _{fc} \cdot k_{c2} \cdot f_{ck}}{γ_c}\]
\[{\eta _{fc}} = {\left( {\frac{{30}}{{{f_{ck}}}}} \right)^{\frac{1}{3}}} \le 1\]
wo:
kc – Globaler Reduktionsfaktor der Druckfestigkeit
kc2 – Reduktionsfaktor aufgrund von Querrissen
fck – Charakteristische Festigkeit des Betonzylinders (in MPa zur Definition von ηfc.
\[ \textsf{\textit{\footnotesize{Fig. 27\qquad The compression softening law.}}}\]
Beton - GZG
Die Analyse zur Gebrauchstauglichkeit enthält bestimmte Vereinfachungen der Werkstoffmodelle, die für die GZT Analyse verwendet werden. Es wird ein perfekter Verbund angenommen, d.h. die Verankerungslänge wird bei der Gebrauchstauglichkeit nicht überprüft.
Weiterhin wird der plastische Zweig der Spannungs-Dehnungs-Kurve von auf Druck belastetem Beton nicht berücksichtigt, während der elastische Zweig linear und unendlich ist. Das Gesetz zur Druckentfestigung wird nicht berücksichtigt. Diese Vereinfachungen verbessern die numerische Stabilität und Berechnungsgeschwindigkeit, verringern jedoch nicht die Allgemeinheit der Lösung, solange die resultierenden Grenzwerte für die Materialspannung bei Gebrauchstauglichkeit deutlich unter ihren Streckgrenzen liegen (wie vom Eurocode gefordert). Daher sind die für die Gebrauchstauglichkeit verwendeten, vereinfachten Modelle nur gültig, wenn alle Anforderungen zur Überprüfung erfüllt sind.
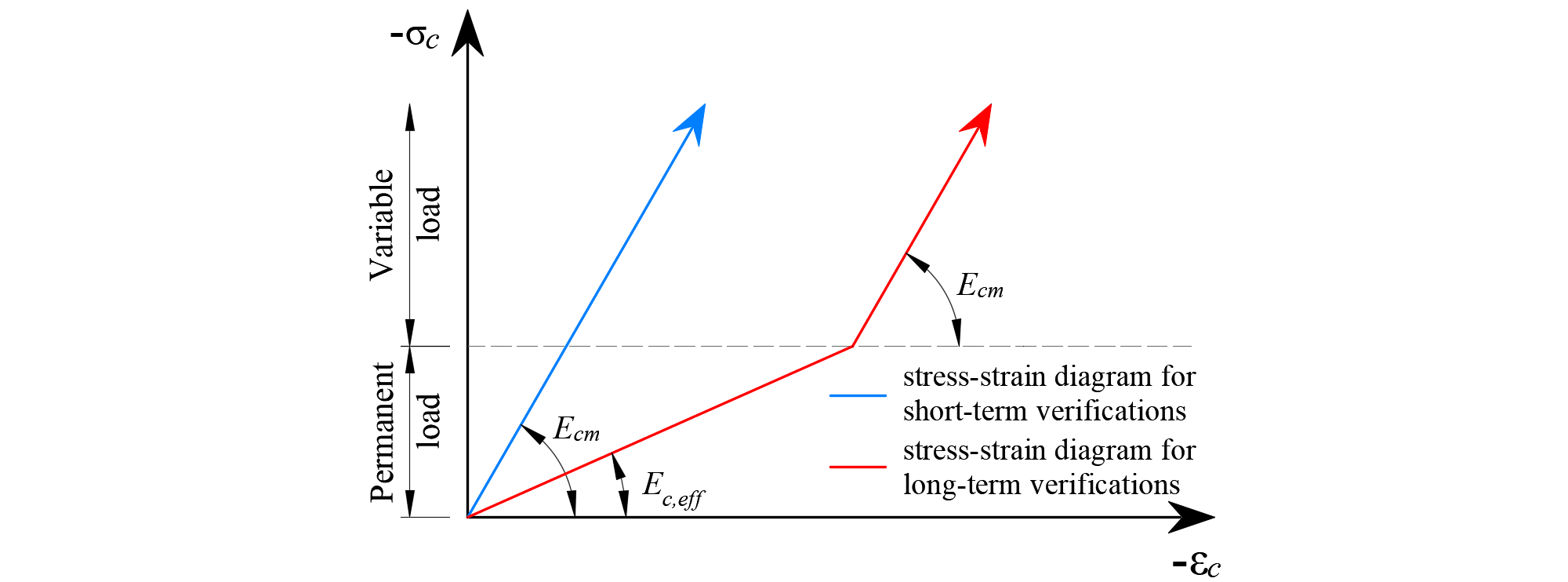
\[ \textsf{\textit{\footnotesize{Fig. 28\qquad Concrete stress-strain diagrams implemented for serviceability analysis: short- and long-term verifications.}}}\]
Langfristige Auswirkungen
Bei der Analyse der Gebrauchstauglichkeit werden die langfristigen Auswirkungen von Beton unter Verwendung eines wirksamen unendlichen Kriechkoeffizienten (φ, standardmäßig mit 2,5 angenommen) betrachtet, der den Sekantenmodul der Elastizität des Betons (Ecm) wie folgt bearbeitet:
\[E_{c,eff} = \frac{E_{cm}}{1+\varphi}\]
Bei der Betrachtung von langfristigen Auswirkungen wird zunächst ein Lastschritt mit allen ständigen Lasten, unter Berücksichtigung des Kriechkoeffizienten (d.h .unter Verwendung des wirksamen E-Mduls von Beton, Ec,eff) berechnet, und anschließend werden die zusätzlichen Lasten ohne den Kriechkoeffizienten berechnet (d.h. unter Verwendung von Ecm). Um kurzfristige Überprüfungen durchzuführen, wird zusätzlich eine weitere Berechnung durchgeführt, bei der alle Lasten ohne den Kriechkoeffizienten berechnet werden. Beide Berechnungen für Langzeit- und Kurzzeitüberprüfungen sind in Abb. 28 dargestellt.
Bewehrung
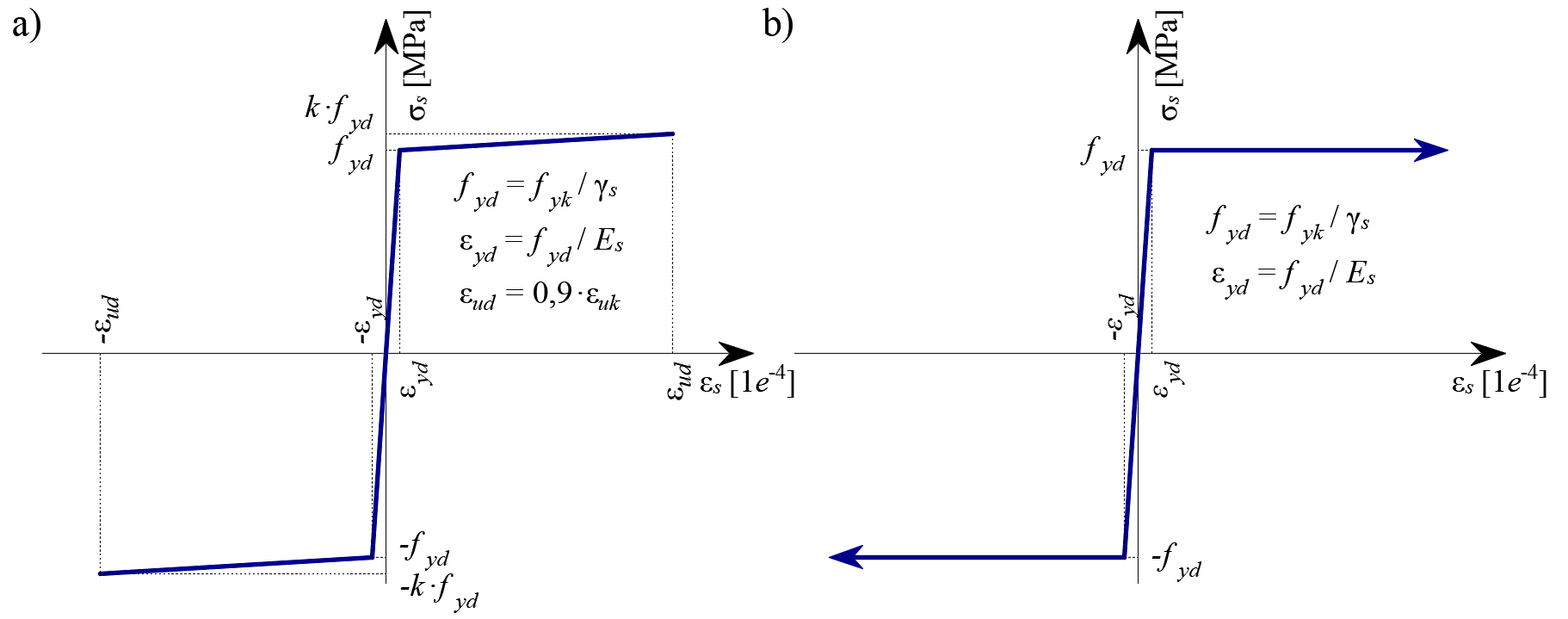
Standardmäßig wird das idealisierte bilineare Spannungs-Dehnungs-Diagramm für die blanken Bewehrungsstäbe berücksichtigt, die typischerweise durch Bemessungsnormen (Abb. 29) definiert sind. Die Definition dieses Diagramms erfordert nur, dass die grundlegenden Eigenschaften der Bewehrung während der Bemessungsphase bekannt sind (Festigkeits- und Duktilitätsklasse). Wann immer bekannt, kann das reale Spannungs-Dehnungs-Verhältnis der Bewehrung (warmgewalzt, kaltverformt, abgeschreckt und selbsttemperiert, etc.) berücksichtigt werden. Das Spannungs-Dehnungs-Diagramm der Bewehrung kann vom Benutzer definiert werden. In diesem Fall ist es jedoch unmöglich, den Effekt der Zugversteifung anzunehmen (eine Berechnung der Rissbreite ist nicht möglich). Die Verwendung des Spannungs-Dehnungs-Diagramms mit horizontalem oberem Ast ermöglicht keine Überprüfung der strukturellen Haltbarkeit. Daher ist eine manuelle Überprüfung der Standardanforderungen an die Duktilität erforderlich.
\( \textsf{\textit{\footnotesize{Fig. 29 \qquad Stress-strain diagram of reinforcement: a) bilinear diagram with an inclined top branch; b) bilinear diagram}}}\) \( \textsf{\textit{\footnotesize{with a horizontal top branch.}}}\)
Zugversteifung (Abb. 30) wird automatisch berücksichtigt, indem das Verhältnis von Eingangsspannung zu Dehnung des blanken Bewehrungsstabs bearbeitet wird, um die durchschnittliche Steifigkeit der im Beton eingebetteten Stäbe (εm) gemäß den in Abschnitt 1.2.4 dargestellten Ansätzen zu erfassen.
\[ \textsf{\textit{\footnotesize{Fig. 30\qquad Scheme of tension stiffening.}}}\]