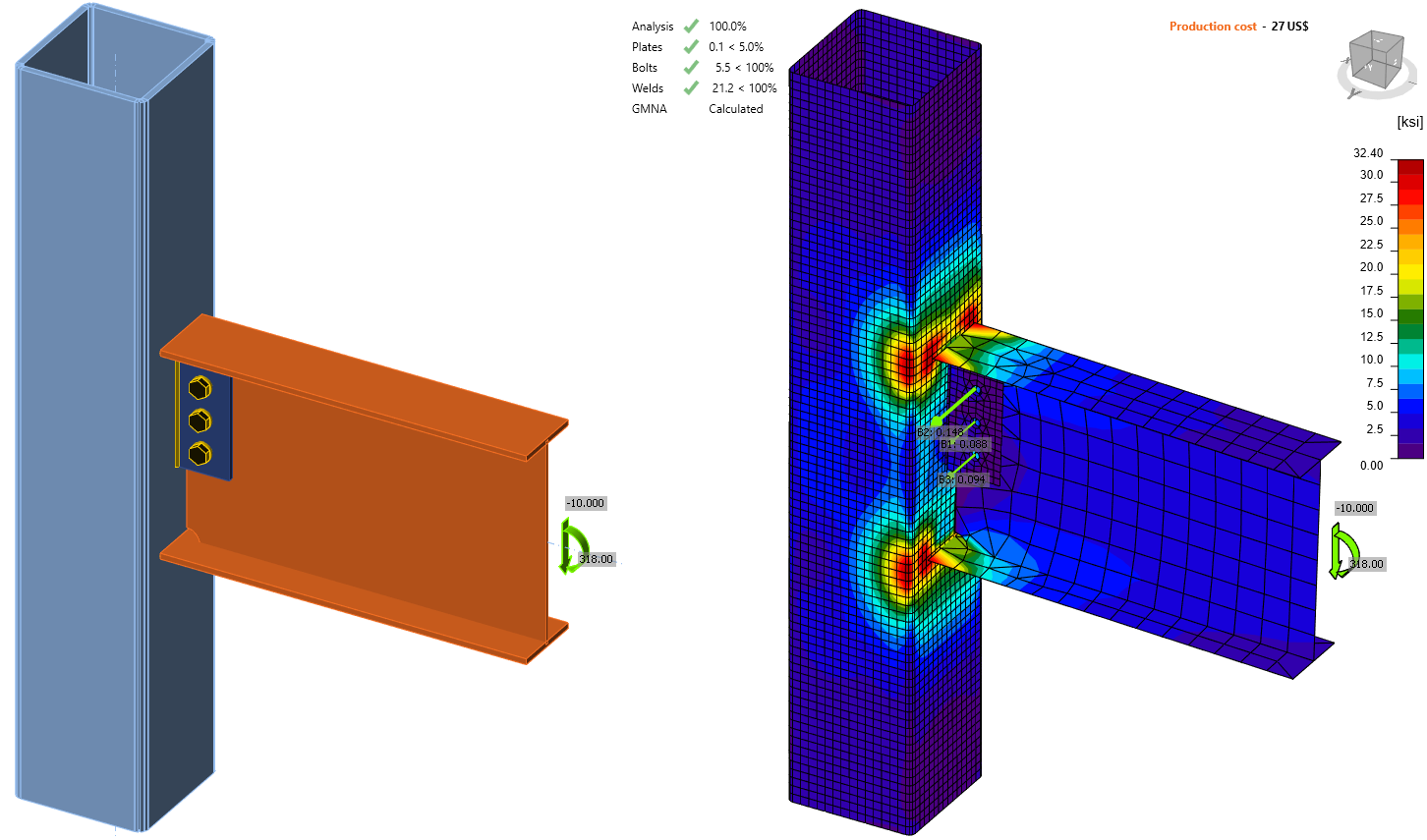
Stiffness analysis - W to HSS moment connection (AISC)
The example is taken from the article Shearly Perfect by Larry S. Muir and Carlo Lini:
W16x31 beam with a span of 30 feet is connected to HSS 10x10x1/2 column and loaded by 10 kips shear force and 318 kip-in bending moment.
This connection is often classified as rigid because the flanges are directly welded to the column. However, the wall of the hollow section column is not directly supported and significantly deforms. The authors provide a very simplified method to estimate the stiffness of this connection:
IDEA StatiCa provides a thorough stiffness analysis based on finite elements. Several values are displayed:
- MEd - set bending moment
- Mj,Rd - connection load resistance
- Sj,ini - initial stiffness assumed as a secant stiffness at 2/3 Mj,Rd
- Sjs - secant stiffness at the set load
- \(\phi\) - rotation at the set load
- \(\phi_c\) - estimated rotation capacity (at 15 % plastic strain of steel plates; note that all other failure modes are neglected - sufficient detailing, strength of welds and bolts must be provided)
- L - length of the analyzed member used for classification according to stiffness
- Sj,R - lower boundary for rigid connection
- Sj,P - upper boundary for pinned connection
According to both approaches, the connection is classified as semi-rigid. The author states: "Based upon this analysis, it is doubtful that the connection can be shown to be a fully restrained connection, although a more accurate model may result in a restraint closer to 20." By closer to 20, the authors mean the value of \(\frac{K_s L}{E I}\) equal to 5.3 in this case. That means the connection is probably more rigid. This is confirmed by the stiffness analysis in IDEA Connection.
It is important to note that full penetration butt welds of beam flanges do not ensure the rigid connection. The stiffness of support, in this case, the wall of HSS, must be also taken into account.
| IDEA Connection | L.S. Muir | IDEA/L.S. Muir | |
| Sj,ini [kip-in/rad] | 131964 | ||
| Sj,s [kip-in/rad] | 180104 | 159000 | 113 % |