Connessioni con bulloni e bulloni precaricati

Bulloni

Nel Metodo agli Elementi Finiti Basato sulle Componenti (CBFEM), il bullone, con il suo comportamento in trazione, taglio e bearing, è il componente descritto dalle molle dipendenti non lineari. Il gruppo bullone è composto da bullone, rondella e dado ed è simulato da una molla non lineare, da elementi a corpo rigido e da elementi di intervallo (gap elements).

Bullone in trazione

Il bullone in trazione è descritto da una molla con la sua rigidezza  assiale iniziale, la resistenza di progetto, l'innescarsi dello snervamento e la capacità di deformazione. La rigidezza assiale iniziale è ricavata analiticamente nella linea guida VDI2230 e in Agerskov (1976).

\[D_{Lb} =\frac{L_s+0.4d_b}{EA_{ss}}\]

\[A_{pp}=\frac{0.75D_H(L_w-D_H)}{D_{W1}^2-D_{W2}^2}\]

\[A_{P1}=\frac{\pi}{4}(D_H^2-D_{W1}^2)\]

\[A_{P2}=\frac{1}{2}(D_{W2}^2-D_H^2)\tan^{-1}A_{pp}\]

\[A_P=A_{P1}+A_{P2}\]

\[D_{LW}=\frac{L_W}{EA_P}\]

\[k=\frac{1}{D_{LB}+D_{LW}}\]

dove:

• \(d_b\) – diametro del bullone
• \(D_H\) – diametro della testa del bullone
• \(D_{W1}\) – diametro interno della rondella
• \(D_{W2}\) – diametro esterno della rondella
• \(L_W\) – spessore della rondella
• \(L_s\) –  lunghezza della parte non filettata del gambo
• \(A_{ss}\) – area lorda del bullone
• \(E\) – Modulo di elasticità di Young

Il modello corrisponde ai dati sperimentali; si veda Gödrich et al. (2014). Per l’innesco dello snervamento e della capacità di deformazione, si presume che la deformazione plastica si verifichi solamente nella parte filettata del gambo del bullone.

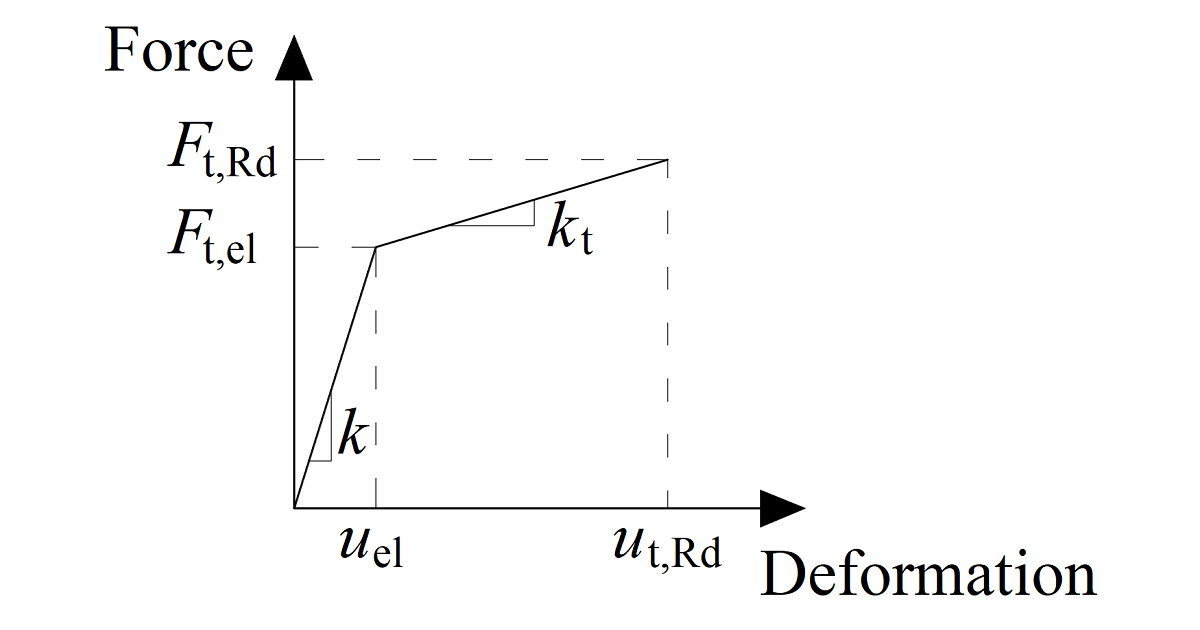
Diagramma forza-deformazione per il carico della piastra

Il diagramma forza-deformazione viene costruito utilizzando le seguenti equazioni:

Rigidezza plastica:

\[ k_t = c_1 k \]

Forza al limite elastico:

\[ F_{t,el} = \frac{F_{t,Rd}}{c_1 c_2 - c_1 +1} \]

Deformazione al limite elastico:

\[ u_{el} = \frac{ F_{t,el} }{k} \]

Deformazione al limite plastico:

\[ u_{t,Rd} = c_2 u_{el} \]

\[ c_1 = \frac{f_{ub} - f_{yb}}{\frac{1}{4} A E - f_{yb}} \]

\[ c_2 = \frac{AE}{4 f_{yb}} \]

dove:

• \(F_{t,Rd}\) – resistenza di progetto del bullone in trazione
• \(f_{yb}\) –  resistenza limite del bullone
• \(f_{ub}\) – resistenza ultima del bullone
• \(A\) – allungamento dopo la frattura

Bullone a taglio

Solo la forza di compressione viene trasferita dal gambo del bullone alla piastra nel foro del bullone. È modellato da interpolazioni tra i nodi del gambo e i nodi sul bordo dei fori. La rigidezza di deformazione dell'elemento shell che modella le piastre distribuisce le forze tra i bulloni e simula il carico adeguato della piastra.

I fori dei bulloni sono considerati standard (predefiniti) o asolati (possono essere impostati nell'editor delle piastre). I bulloni nei fori standard possono trasferire la forza di taglio in tutte le direzioni, mentre i bulloni nei fori asolati hanno una direzione esclusa e possono muoversi liberamente nella direzione selezionata.

La rigidezza iniziale e la resistenza di progetto di un bullone a taglio sono definite dalle seguenti formule:

\[k_{el}=\frac{1}{\frac{1}{k_{11}}+\frac{1}{k_{12}}}\]

\[k_{11} = \frac{8d_b^2f_{ub}}{d_{M16}}\]

\[k_{12}=12k_td_bf_{up}\]

\[k_t=\min \left ( 2.5,\, \frac{1.5t_{min}}{d_{M16}} \right ) \]

\[k_{pl}=\frac{k_{el}}{1000}\]

dove:

• \(d_b\) – diametro del bullone
• \(f_{ub}\) – resistenza ultima del bullone
• \(d_{M16}=16 \textrm{ mm}\) – diametro del bullone di riferimento M16
• \(f_{up}\) – resistenza ultima della piastra collegata
• \(t_{min}\) – spessore minimo della piastra collegata 

The spring representing the bolt in shear has bi-linear force deformation behavior. Initialization of yielding is expected at:

La molla che rappresenta il bullone a taglio ha un comportamento bi-lineare di deformazione della forza. L'inizio dello snervamento è previsto a:

\[F_{V,el}=0.999 F_{V,Rd}\]

La capacità di deformazione è considerata come:

\[\delta_{pl}=\delta_{el}\]

dove:

• \(F_{V,el}\) – resistenza elastica del bullone a taglio
• \(F_{V,Rd}\) – resistenza di progetto del bullone a taglio
• \(\delta_{el}\) – deformazione elastica del bullone a taglio

Interazione tra razione e taglio

L'interazione tra la forza assiale e quella di taglio può essere introdotta direttamente nel modello di analisi. La distribuzione delle forze riflette meglio la realtà (vedi diagramma allegato). I bulloni con un'elevata forza di trazione assorbono meno forza di taglio e viceversa.

Esempio di interazione tra forza assiale e di taglio (EC)

Bulloni precaricati

I bulloni precaricati sono utilizzati nelle unioni ad attrito nei casi in cui è necessario ridurre al minimo la deformabilità della struttura. Il modello di trazione in questo caso è lo stesso dei bulloni standard. La forza di taglio non viene trasferita tramite bearing bensì tramite attrito tra le piastre serrate.

La resistenza allo slittamento di progetto di un bullone precaricato è influenzata da una forza di trazione applicata.

IDEA StatiCa Connection verifica lo stato limite di pre-slittamento dei bulloni precaricati. Se si osserva un effetto di slittamento, i bulloni non soddisfano la verifica. In seguito, deve essere verificato lo stato limite post-slittamento, effettuando una verifica standard dei bulloni in bearing, in cui i fori dei bulloni sono caricati in modo portante e i bulloni in taglio.

L'utente può decidere quale stato limite controllare tra la resistenza allo scorrimento importante o lo stato di post-scorrimento a taglio dei bulloni. Entrambe le verifiche su uno stesso bullone non sono combinate in un'unica soluzione. Si presume che il bullone abbia un comportamento standard dopo uno scorrimento importante e che possa essere verificato con la procedura di carico standard.

Il carico del momento della connessione ha una leggera influenza sulla capacità a taglio. Tuttavia, viene risolta semplicemente in modo separato una verifica dell'attrito su ciascun bullone. Questa verifica è implementata nel componente FEM del bullone. Non vi sono informazioni generali sul fatto che il carico di trazione esterno di ciascun bullone derivi dal momento flettente o dal carico di trazione della connessione.

Distribuzione delle tensioni in una connessione a taglio con bulloni standard

Distribuzione delle tensioni in una connessione ad attrito con bulloni a taglio