Principes van krachten in de verbinding: Evenwicht, dragende staaf, ondersteuningen

1 Rekenmodel

Het rekenmodel in IDEA StatiCa Connection kent, zoals elk ander eindige-elementenmodel, randvoorwaarden en belastingen. We laten zien hoe het model is opgebouwd met een concreet voorbeeld.

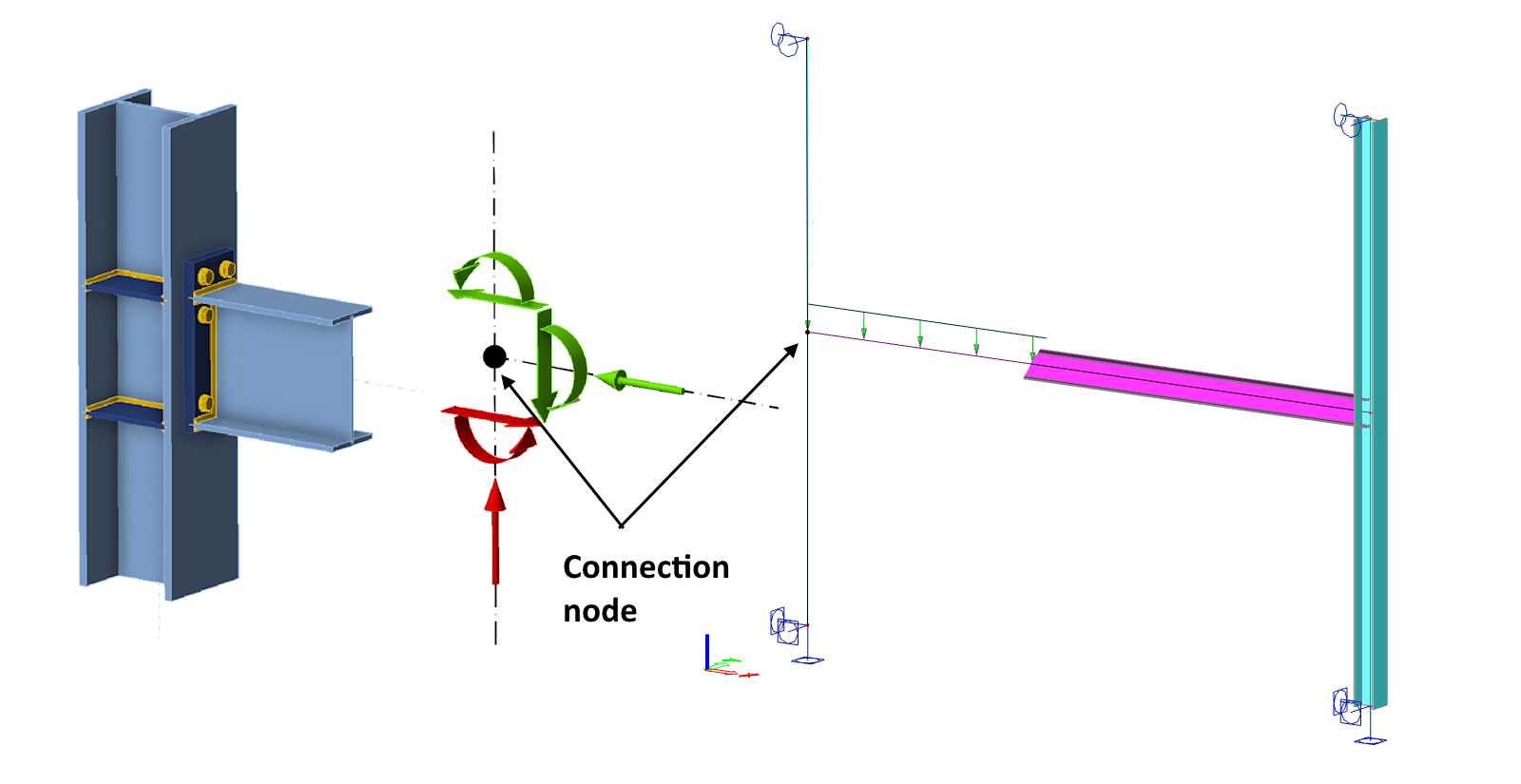
Beschouw het volgende eenvoudige staafmodel, waarin een horizontale ligger middels een momentvaste verbinding met een kolom is verbonden. De ligger is belast met een gelijkmatig verdeelde belasting, en de momentverbinding wordt gerealiseerd met een kopplaat.

Onderstaande afbeelding geeft een visualisatie van deze verbinding weer.

In Connection app wordt het 3D rekenmodel van de verbonden staaf belast met interne krachten die werken in de individuele staven direct bij het verbindingsknooppunt. Het middelpunt van de verbinding, voorgesteld door een zwarte bol in de wireframe weergave, is dus identiek aan het knooppunt in het globale FEM staafmodel.

Er kunnen twee verschillende benaderingen worden gebruikt.

• De belasting van de verbinding is in evenwicht
• De belasting van de verbinding is niet in evenwicht

De twee benaderingen verschillen in randvoorwaarden en belastingaanpak. Met de knop Lasten in evenwicht in de bovenste werkbalk kan tussen beide modelvarianten worden geschakeld.

Het artikel bespreekt eerst in detail de randvoorwaarden en belasting van het rekenmodel dat overeenkomt met de optie Lasten in evenwicht AAN. Met deze optie kan de gehele verbinding als één geheel worden beoordeeld en worden alle verbonden staven belast. Dit is de standaardinstelling van het programma nadat een nieuw project is gemaakt.

Grensvoorwaarden en de manier waarop het rekenmodel wordt belast met de optie Lasten in evenwicht op UIT worden in detail besproken in hoofdstuk 3. Deze variant van modelleren is bijvoorbeeld geschikt voor het controleren van de afzonderlijke verbindingen van individuele elementen.

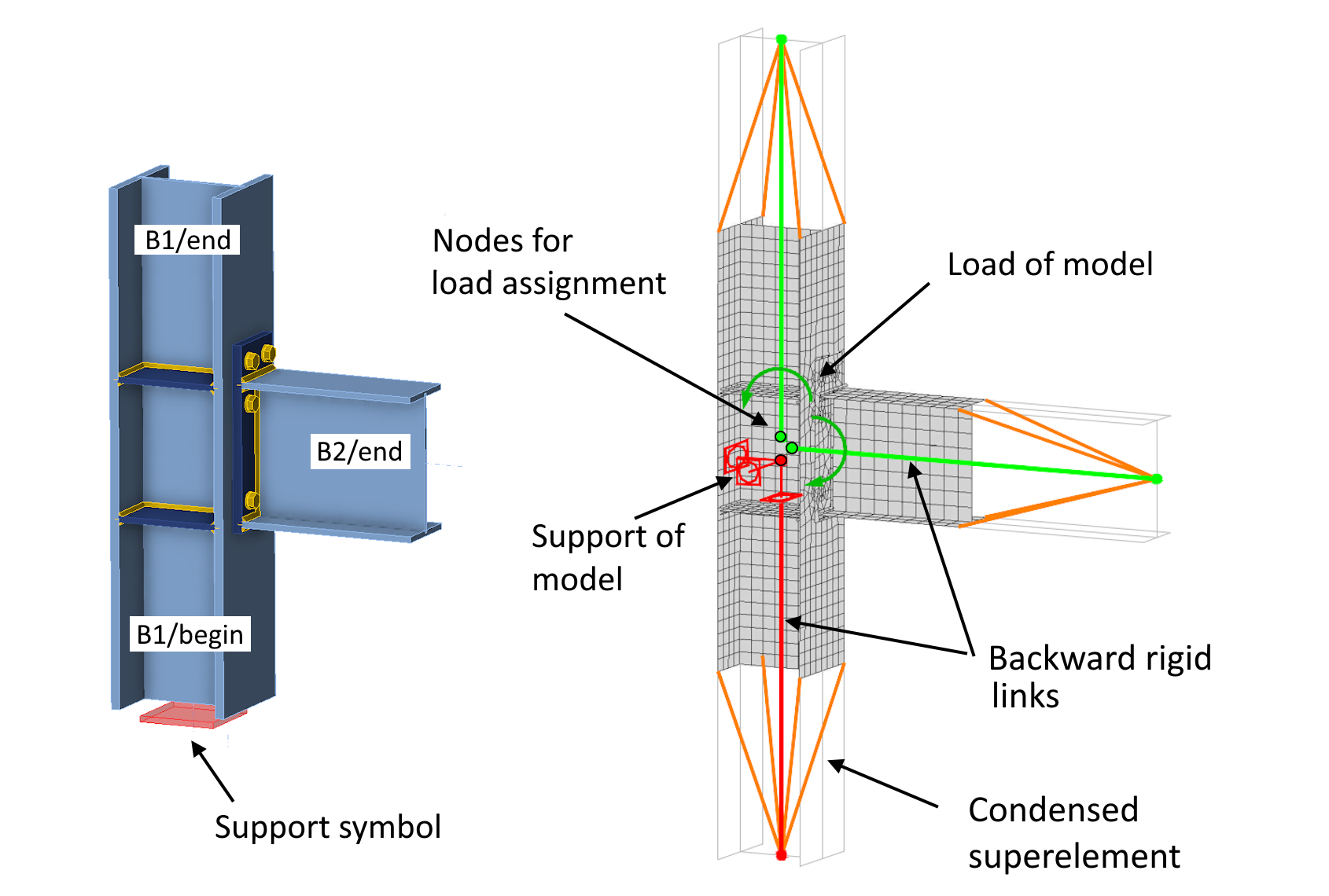
In het voorbeeld bestaat de verbinding uit een doorgaande staaf (kolom B1) en een eindige staaf (balk B2). De kolom is ingesteld als dragend element (wordt later uitgelegd). Het rekenmodel wordt schematisch weergegeven in de volgende afbeelding.

Het rekenmodel van de verbinding met de eindige-elementenmethode (FEM) bestaat uit:

1. Verbonden staven- Een constructie-element (bijvoorbeeld een balk, kolom of schoor) dat op de verbinding aansluit, wordt gemodelleerd. De doorsnede wordt daarbij opgebouwd met behulp van eindige schaalelementen.
2. Onderdelen van de verbinding - Eindplaten, hoekplaten, verstijvers, ribben, enz. Wederom gemodelleerd met behulp van eindige schaalelementen.
3. CBFEM onderdelen - Lassen, bouten, contacten, MPC (Multi-Point Constraint), enz. Deze onderdelen van het model staan niet centraal in dit artikel en worden beschreven in de theoretische achtergrond.
4. Condensed Superelements (gecondenseerde superelementen) - Zorgen voor een realistische en gelijkmatige verdeling van puntbelastingen binnen het 3D-model van de aangesloten staaf. Deze elementen zijn niet zichtbaar voor de gebruiker en worden uitgebreider toegelicht in dit artikel.
5. Backward Rigid Link (achterwaartse stijve koppeling)- De uiteinden van het aangesloten element zijn gekoppeld aan hulpknooppunten in het midden van de verbinding via stijve koppelingen (Rigid links). Elke rigid link is verbonden met een eigen hulpknooppunt. De randvoorwaarden van het rekenmodel worden op deze knooppunten toegepast, net als de belasting, in de vorm van puntkrachten en momenten.
6. Supports (Ondersteuningen) - Randvoorwaarden van het CBFEM model toegepast op het beginknooppunt van de stijve koppeling.

1.1 Ondersteuningen

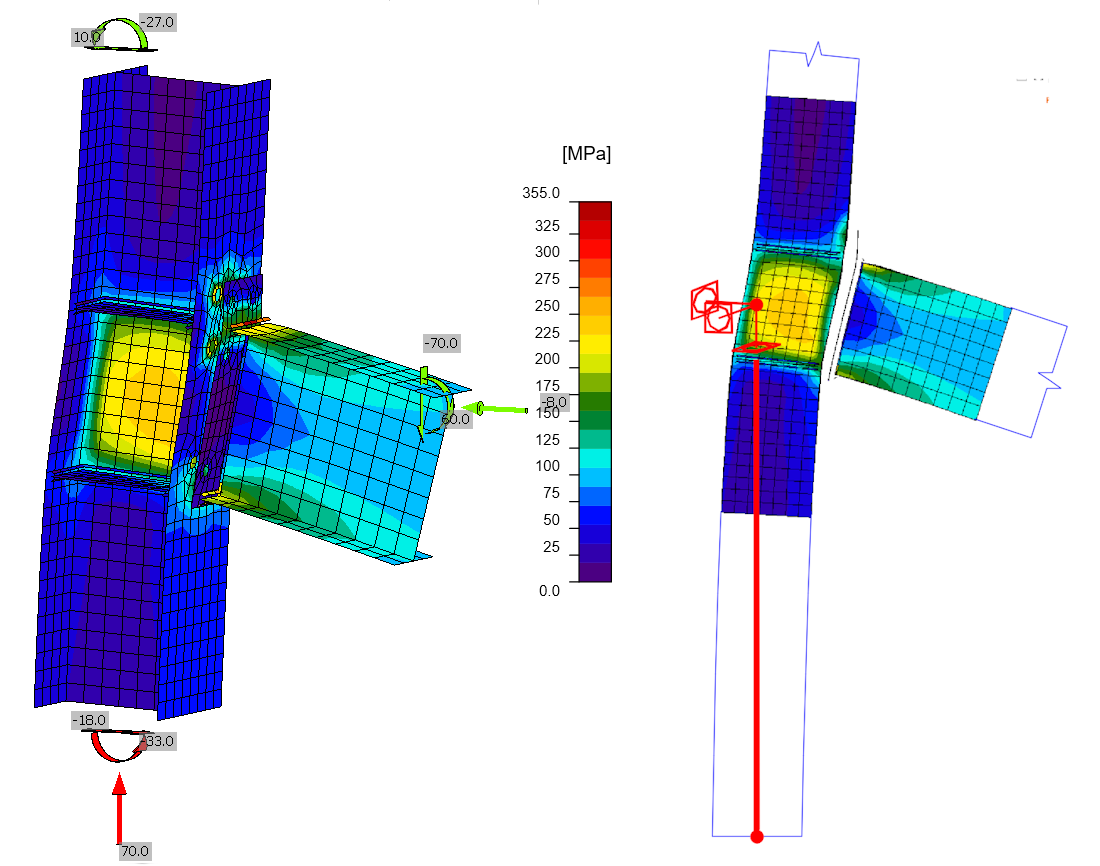
Elk FEM rekenmodel heeft supports nodig om een singulariteit te voorkomen. Het CBFEM model is in principe een algemeen 3D FEM model, wat betekent dat het drie steunen nodig heeft tegen translaties en drie tegen rotaties. Zoals geïllustreerd in de figuur, wordt in ons voorbeeld een puntondersteuning (drie translaties en drie rotaties) gedefinieerd op het beginknooppunt van de achterwaartse stijve koppeling die het onderste uiteinde van de kolom en het midden van de verbinding verbindt.

De beslissing over welke staaf de ondersteuning krijgt, wordt bepaald door welk verbonden element is ingesteld als de zogenaamde dragende staaf. Het ondersteunde uiteinde van de dragende staaf wordt gevisualiseerd met een rood vierkant in het model.

1.2 Belasting

Zoals reeds vermeld, wordt het model in Connection belast door interne krachten in de individuele staven direct bij het verbindingsknooppunt (let op: in de solid view worden de belastingskrachten en -momenten weergegeven aan de uiteinden van de gevisualiseerde verbonden elementen, wat misleidend kan zijn bij het eerste gebruik van de applicatie).

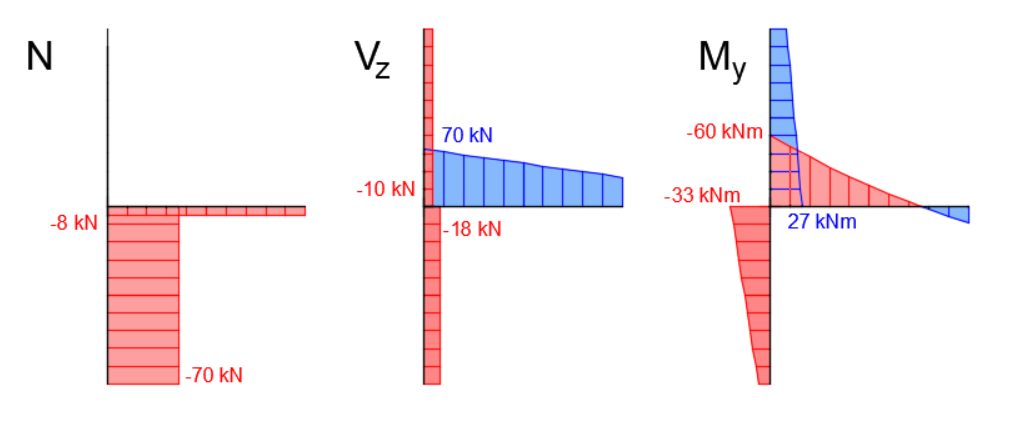
De interne krachten in het besproken model, berekend door het globale FEM-model, zijn als volgt.

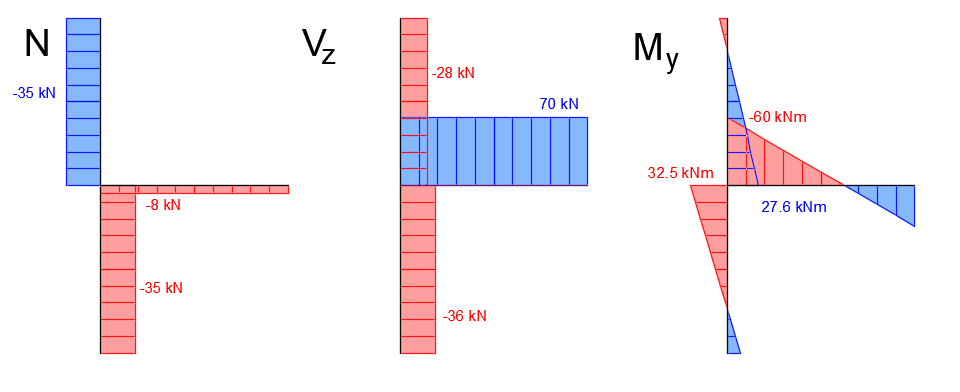
De diagrammen van de interne krachten in meer detail rond de verbinding, samen met de numerieke waarden direct bij de verbindingsknoop zijn:

De krachten uit het globale FEM-model, die als belasting in Connection worden toegepast, zijn weergegeven in de onderstaande figuur.

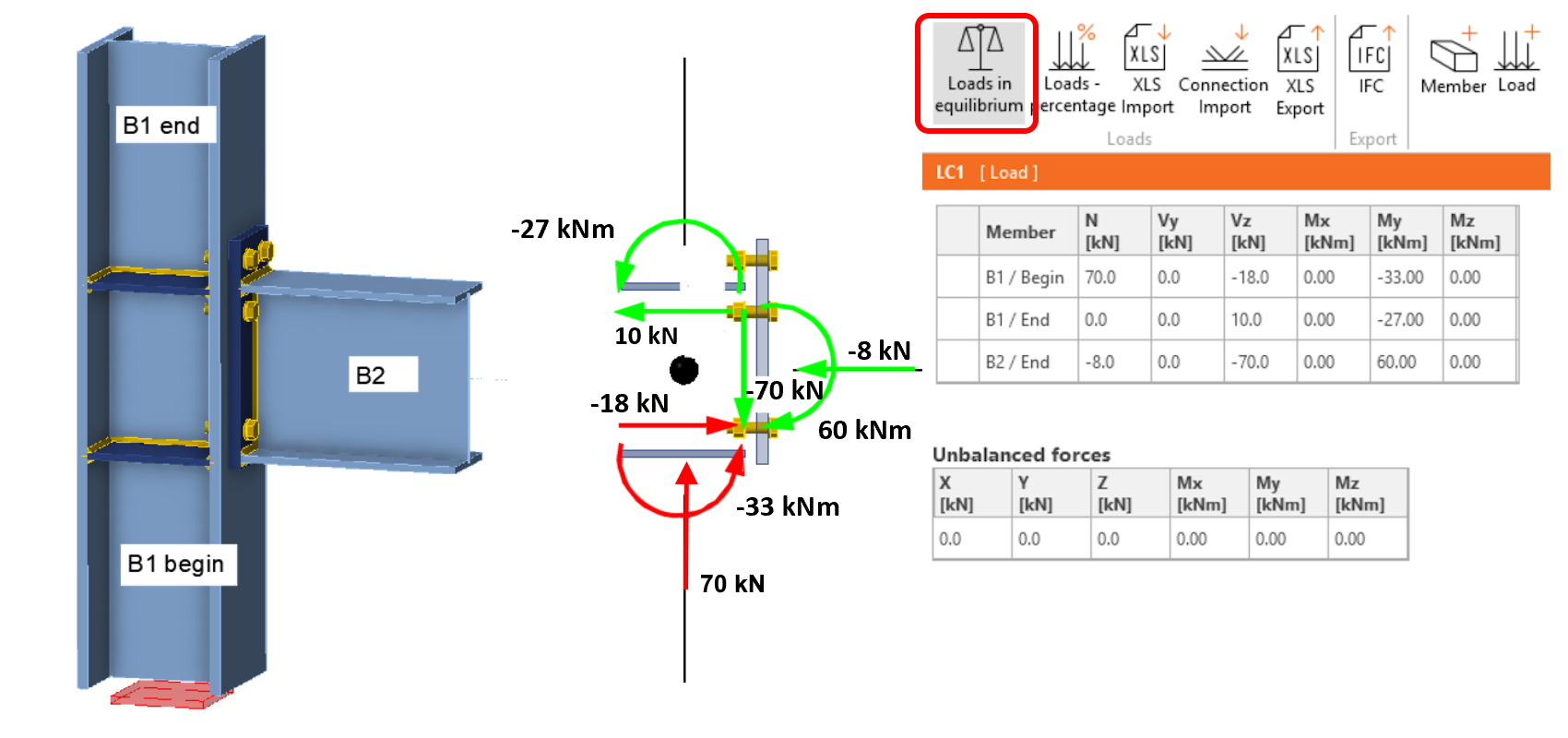
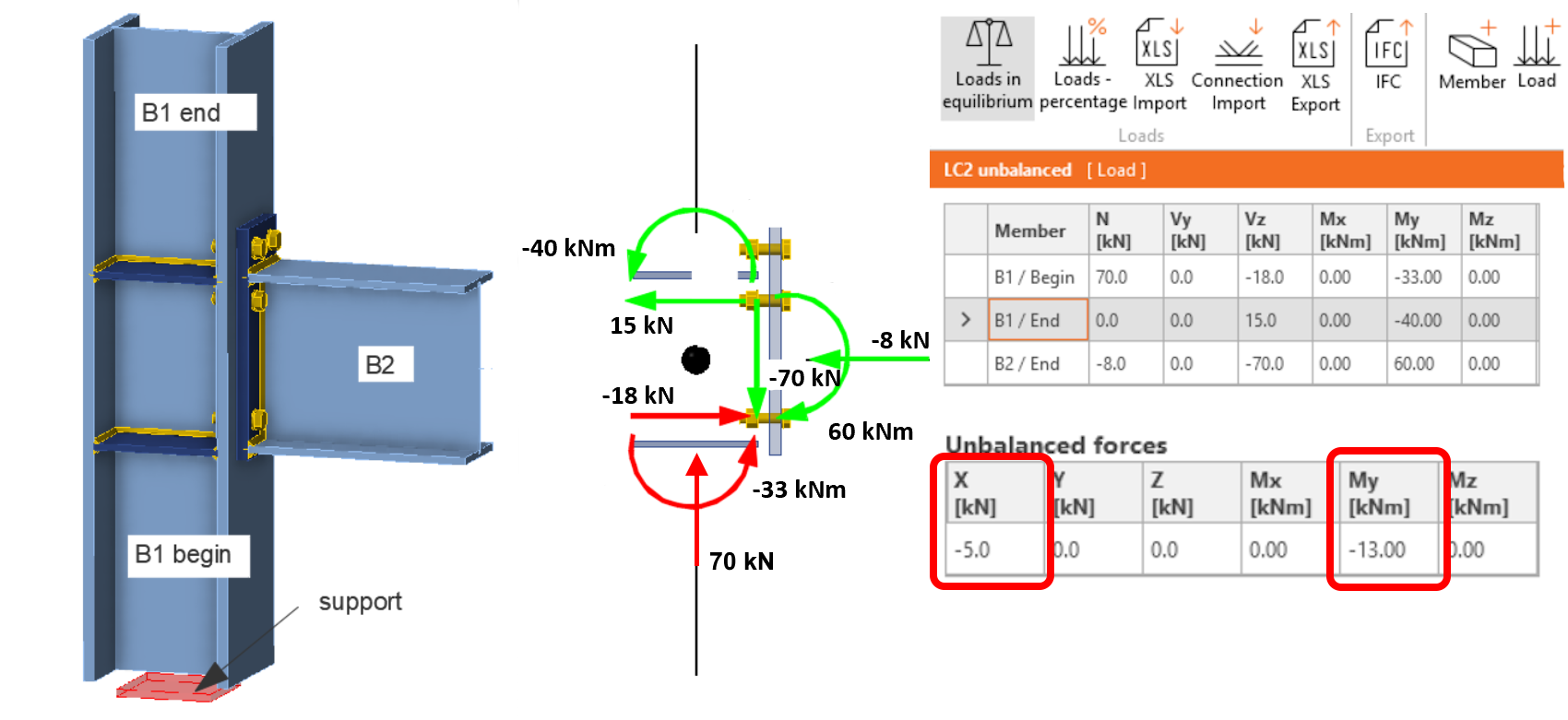
Bij gebruik van de functie Lasten in evenwicht worden interne krachten ingesteld voor alle staven van de verbinding. Een correct gespecificeerde belasting moet dan voldoen aan een basisprincipe: de krachten in de verbindingsknoop moeten in evenwicht zijn. Het voldoen aan deze regel is erg belangrijk voor het juiste ontwerp van de verbinding. De applicatie controleert of aan het evenwicht is voldaan en toont ook een tabel met de ongebalanceerde krachten. Als de belasting van de verbinding correct is gedefinieerd, zijn de ongebalanceerde krachten nul (of bijna nul). 

De belasting van onze verbinding is weergegeven in de volgende figuur, de ongebalanceerde krachten zijn nul, dus de belasting is correct gedefinieerd. We zullen later aan de hand van twee voorbeelden bespreken wat het effect is van een onjuist gespecificeerde belasting wanneer er ongebalanceerde krachten in het model optreden en waarom ze een volledig verkeerd ontwerp van de verbinding kunnen veroorzaken.

De belasting wordt toegepast op de beginknopen van de achterwaartse stijve koppelingen die het verbindingscentrum en het uiteinde van het gecondenseerde superelement verbinden. Met andere woorden, de interne krachten in de individuele staven (in het midden van de verbinding), die gedefinieerd zijn in de belastingstabel, worden direct in het rekenmodel gezet. De achterwaartse stijve koppelingen zorgen er dan voor dat het buigmoment vanuit het verbindingscentrum wordt getransformeerd naar het buigmoment aan het eind van het gecondenseerde superelement. 

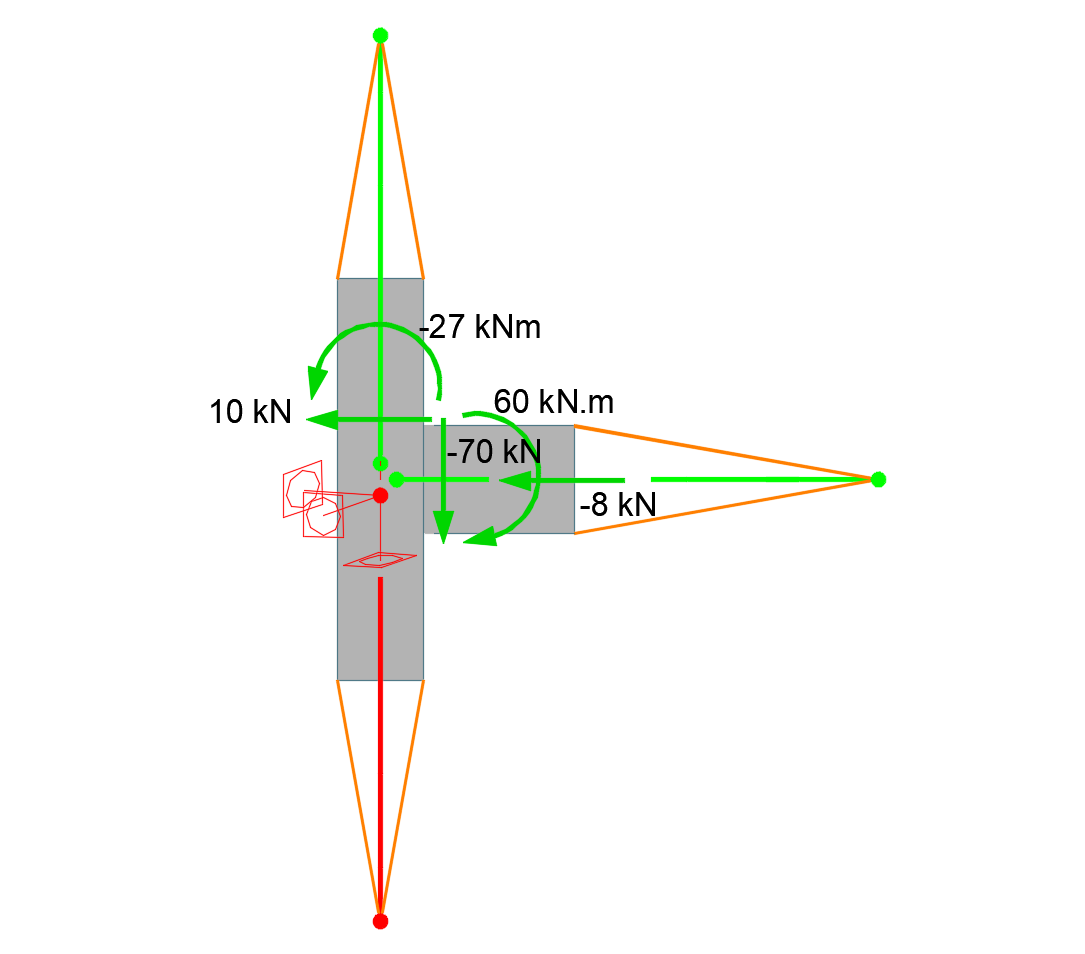
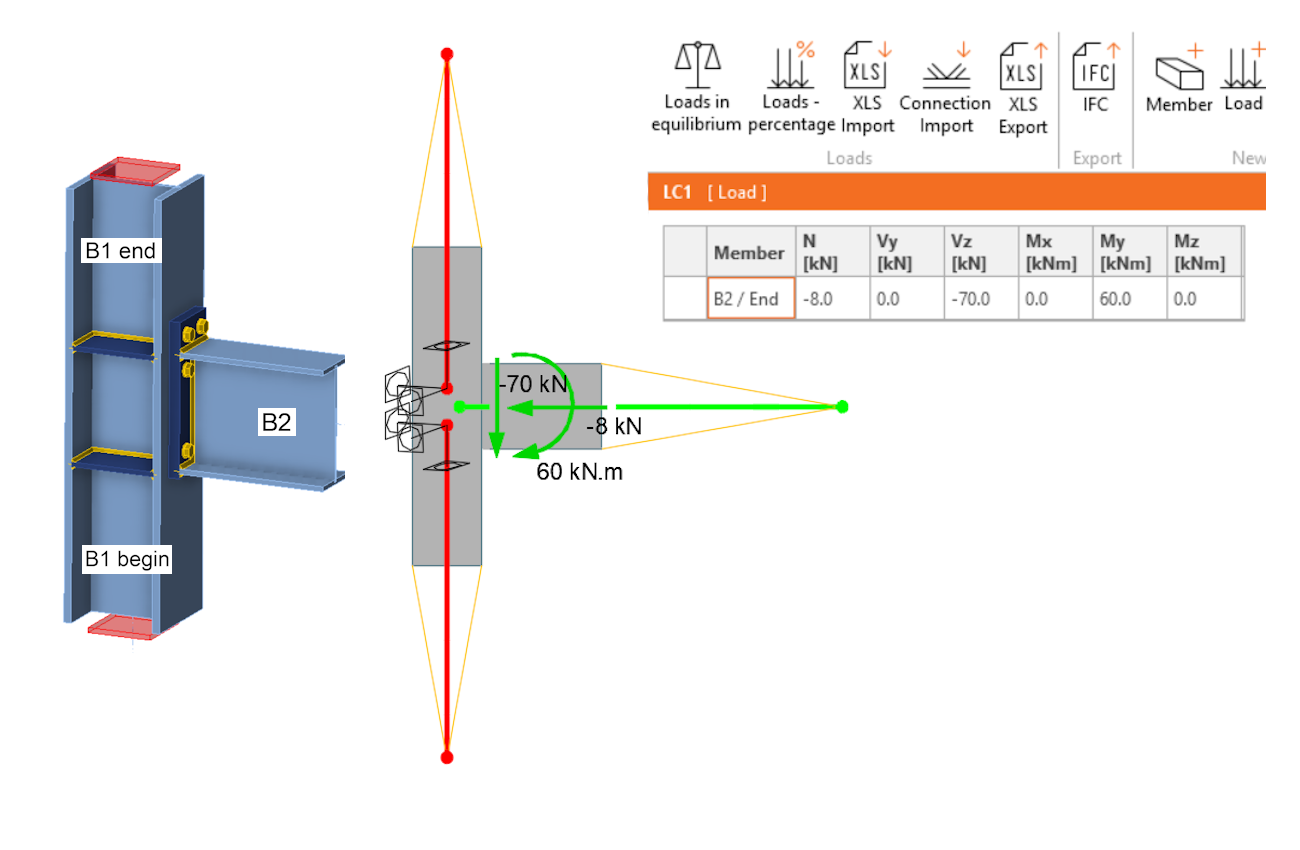
Laten we de functie van de achterwaartse stijve koppeling duidelijker illustreren aan de hand van een eenvoudig balkmodel, waarbij het horizontale element B2 wordt voorgesteld door een vereenvoudigd balkelement in plaats van het 3D-model. De interne krachten op het element in het midden zijn overgenomen uit het voorbeeld: Vz = -70 kN, My = 60 kN.m. Deze kracht en dit moment worden ingesteld aan het begin van de stijve koppeling. Van daaruit worden ze overgebracht naar het uiteinde van het gecondenseerde superelement en vervolgens naar het model van het verbonden element B2. Zoals te zien is, zijn de interne krachten in element B2 aan het begin (midden van de verbinding) dan identiek aan de ingevoerde puntbelastingen.

Het is duidelijk dat het resulterende 3D rekenmodel extern statisch bepaald is (er worden slechts zes vrijheidsgraden genomen) en het model kan vrij vervormen zonder secundaire reacties te veroorzaken die het gedefinieerde krachtenspel zouden veranderen. Het is ook duidelijk dat het specificeren van belastingen op het beginknooppunt van de B1/begin achterwaartse stijve koppeling, waar de modelsteunen worden gespecificeerd, nutteloos zou zijn omdat de krachten en momenten direct door de supports zouden worden opgevangen. Het rekenmodel wordt dus belast met krachten in B1/eind en B2/eind, wat betekent dat slechts twee van de drie staven worden belast, de derde staaf wordt ondersteund. Echter, als de belasting van de verbinding correct is, en de gespecificeerde krachten en momenten in evenwicht zijn, zullen de reacties berekend in de steunen B1/begin identiek zijn aan de belasting gedefinieerd in de tabel. De belasting van het rekenmodel van de verbinding is dan als volgt:

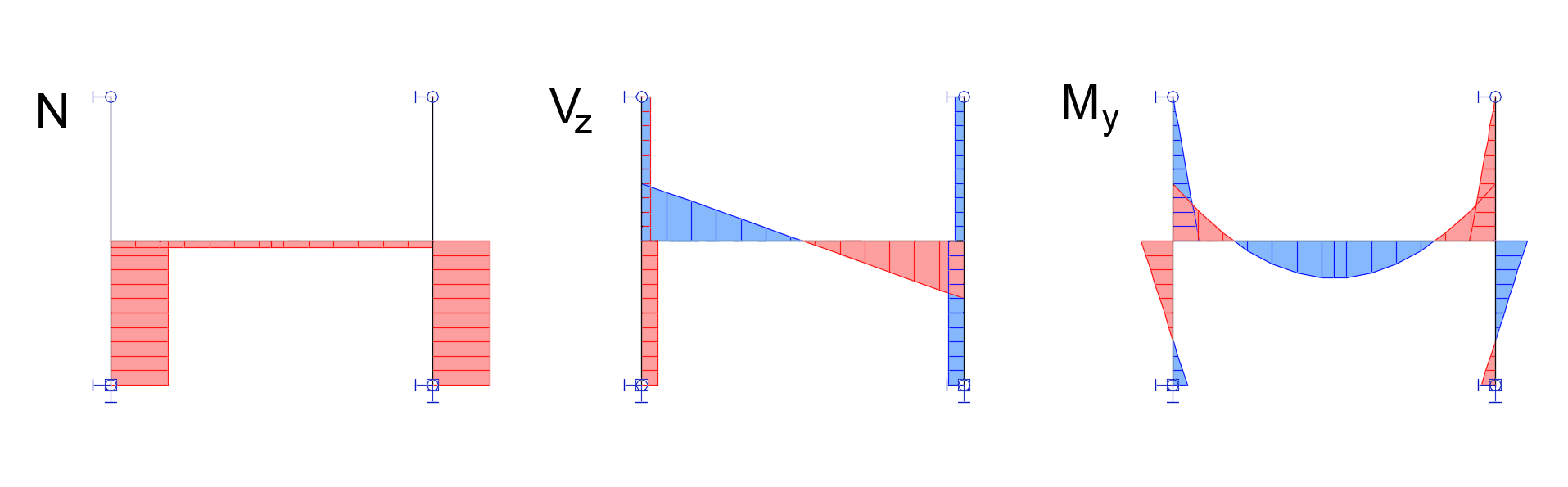
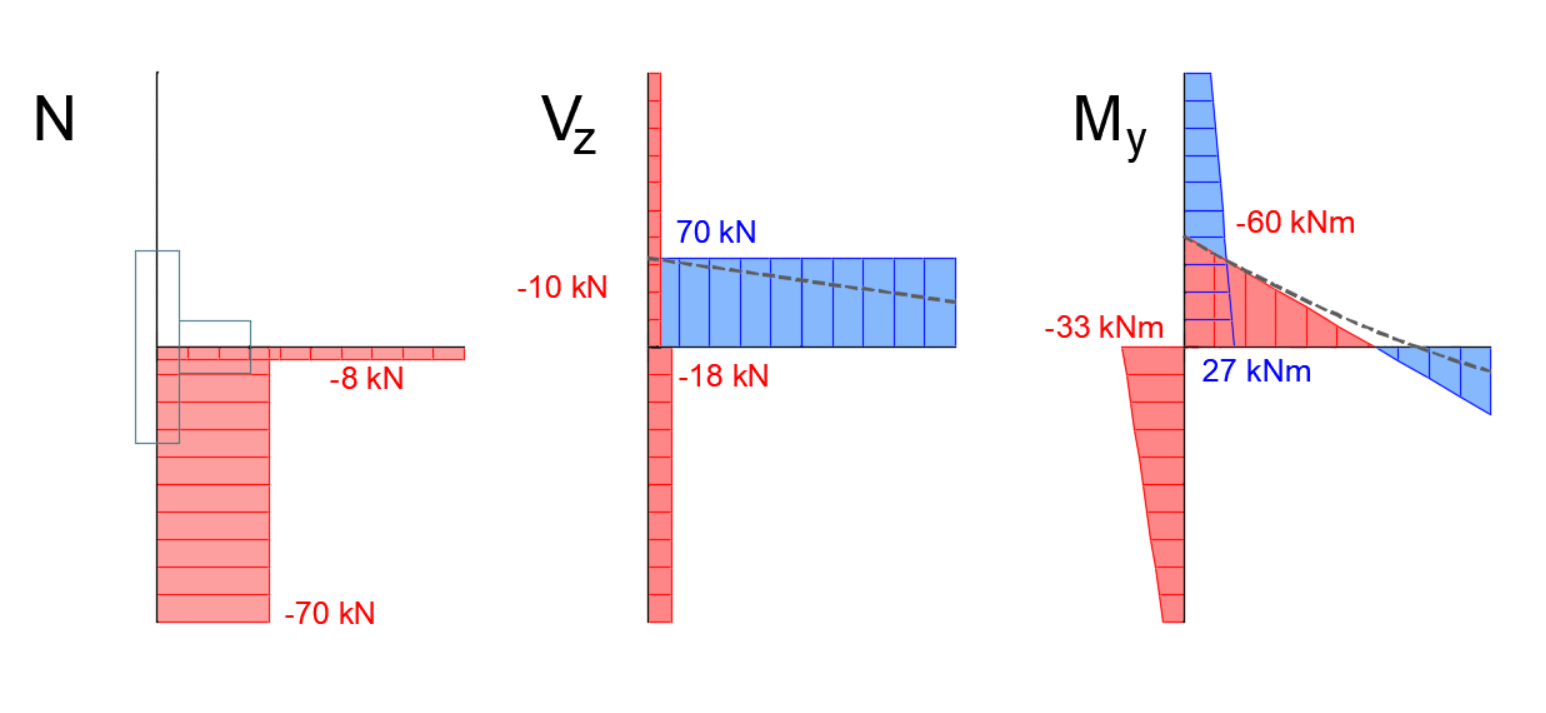
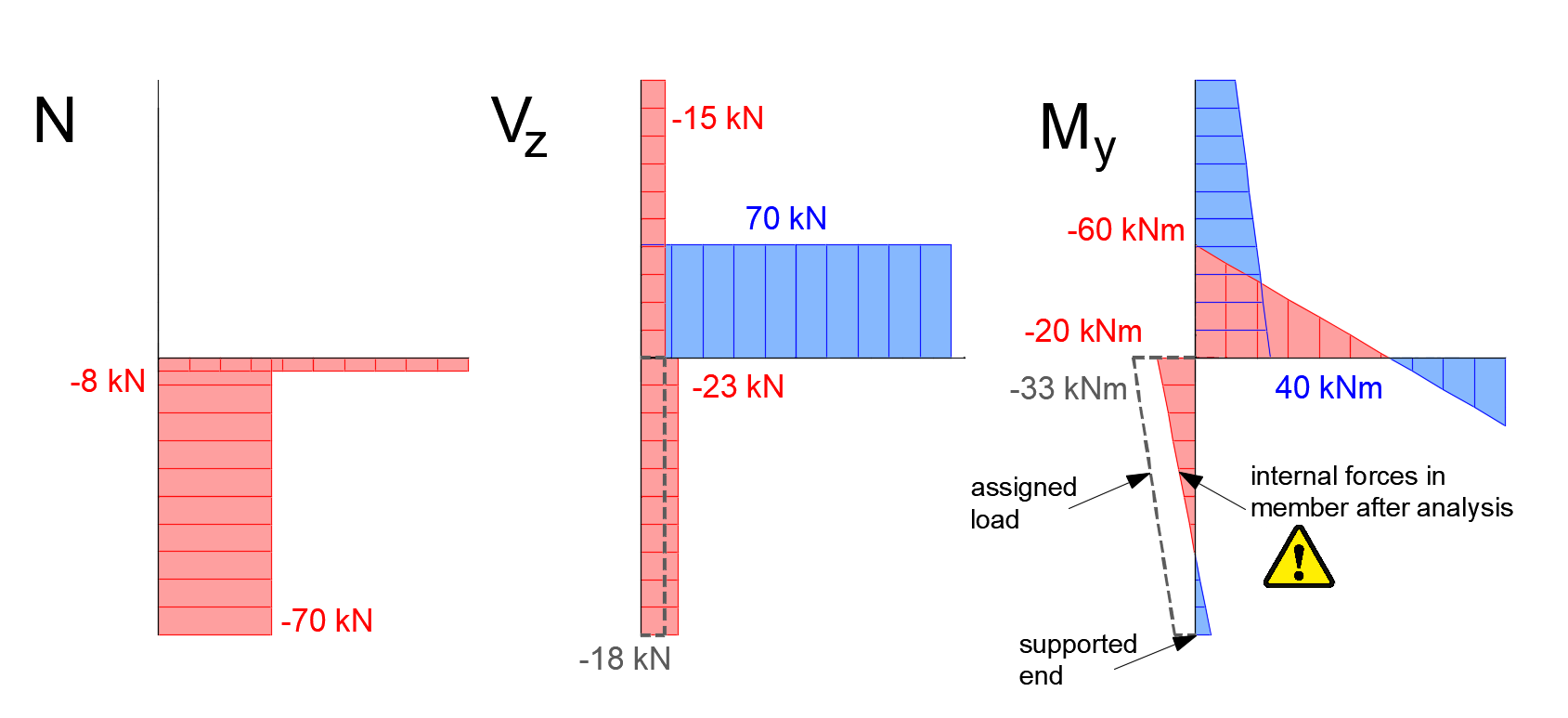
De interne krachtverdeling in het model van de balk is weergegeven in de onderstaande figuur. Ter vergelijking zijn ook de interne krachten uit het globale FEM-model, zoals eerder in dit artikel gepresenteerd, weergegeven als stippellijnen.

Doordat in Connection geen gelijkmatig verdeelde belasting op de balk wordt aangebracht, is de momentlijn lineair in plaats van parabolisch, zoals in het globale model. Wel komt de lijn goed overeen met de parabolische momentverdeling op het aansluitpunt. Op vergelijkbare wijze is de dwarskrachtverdeling in Connection constant, terwijl deze in het globale model een lineair verloop heeft.

Ter illustratie toont onderstaande figuur de vervormde geometrie na berekening. Hieruit is duidelijk af te leiden dat de ondersteuning zich aan de onderzijde van de kolom bevindt, terwijl deze in het rekenmodel feitelijk is gepositioneerd in het midden van de verbinding, via een backward rigid link.

2 Pas op voor ongebalanceerde krachten

We hebben laten zien hoe het FEM-rekenmodel van de verbinding er in principe uitziet, hoe het wordt ondersteund en hoe het wordt belast. In het bovenstaande voorbeeld was de gespecificeerde belasting in evenwicht. We zullen nu het effect op de modelbelasting en de spanningstoestand van de verbinding laten zien als de gespecificeerde belasting niet in evenwicht is.

2.1 Ongebalanceerde krachten in de verbinding

We gebruiken hetzelfde voorbeeld van een momentvaste verbinding met een kopplaat. De gespecificeerde, opzettelijk onjuiste, verbindingsbelasting wordt getoond in de onderstaande figuur. In de tabel voor ongebalanceerde krachten vermeldt het programma de volgende berekende krachten Fx = -5 kN en My = 13kNm.

De verdeling van interne krachten in het model onder een dergelijke belasting zal opnieuw worden gedemonstreerd aan de hand van een vereenvoudigde balkweergave van het verbindingsmodel.

Aan de onderkant van de kolom (B1/begin, het ondersteunde uiteinde van het dragende element) wordt het diagram van het buigend moment en de dwarskracht afgeleid van de krachten ingevoerd in de belastingstabel ook gevisualiseerd door een stippellijn. Het is duidelijk dat de buigende momenten die werkelijk op de kolom werken aanzienlijk verschillen van wat is gespecificeerd op B1/begin in de tabel. Deze verschillen komen precies overeen met de ongebalanceerde krachten van het moment My en de dwarskracht Vz. Hoe komt dat? 

Zoals eerder uitgelegd, worden de interne krachten die gespecificeerd zijn aan de ondersteunde kant van het dragende element (B1/begin) niet daadwerkelijk toegepast op het model. In plaats daarvan resulteren de interne krachten uit de FEM-modelberekening als reacties in de steunen van het rekenmodel. En natuurlijk zijn deze reacties in evenwicht met de belasting gedefinieerd op B2 en B1/eind. Het effect van ongebalanceerde krachten in dit voorbeeld is dus dat het ondersteunde dragende element wordt onderworpen aan heel andere (lagere) interne krachten dan die de gebruiker heeft ingevoerd in de belastingtabel. Daarom moet altijd worden gestreefd naar nul of minimale ongebalanceerde krachten in de verbinding.

Voor de volledigheid moet worden toegevoegd dat in dit specifieke geval de horizontale balkverbinding zelf (bouten, eindplaat, lassen) correct wordt geëvalueerd omdat precies dezelfde belasting die is opgegeven voor het B2-element in de belastingtabel ook wordt toegepast op dit element in het rekenmodel.

2.2 Ongebalanceerde krachten in een vakwerkverbinding

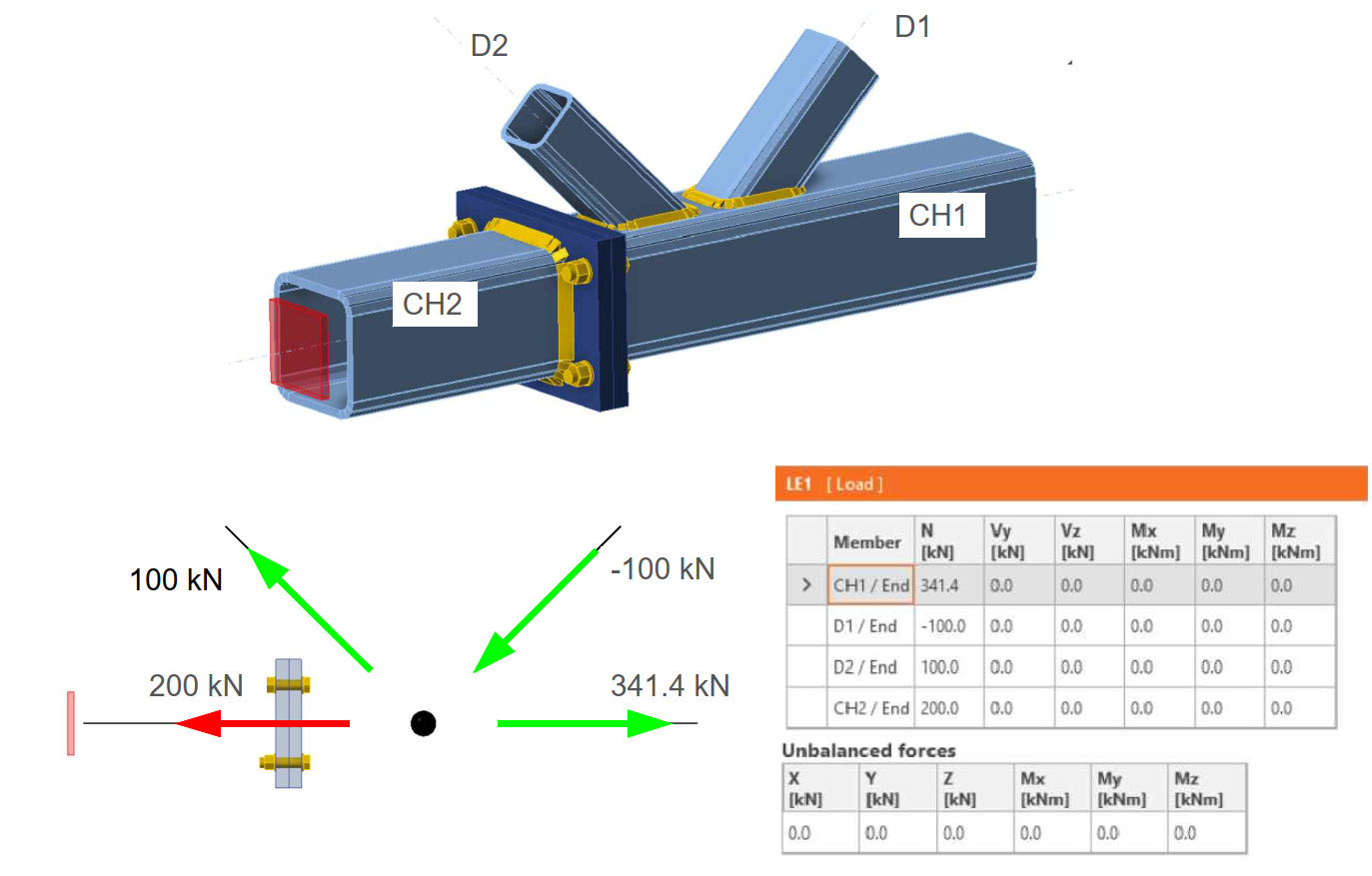
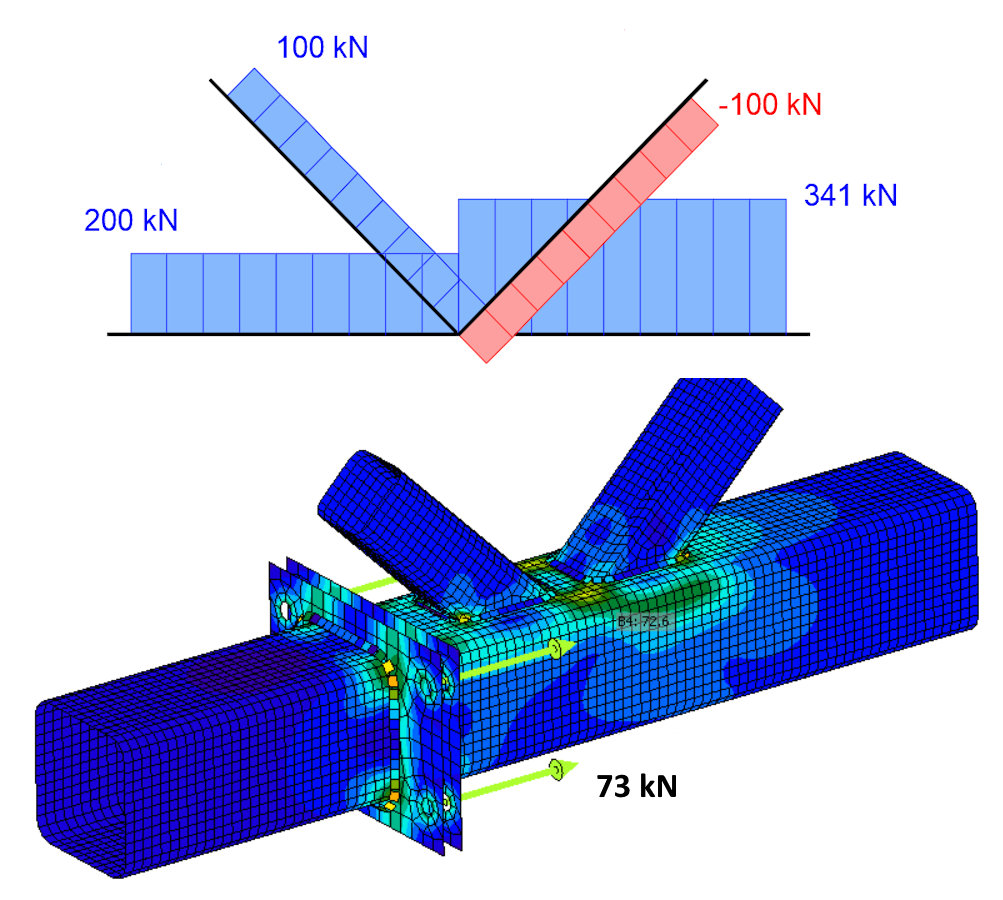
Dit voorbeeld illustreert een geval waarbij een onjuist gespecificeerde belasting met ongebalanceerde krachten in een verbinding leiden tot een volledig onjuist ontwerp van de verbinding. We gebruiken de volgende verbinding, bestaande uit een onderste trekstaaf, een trekdiagonaal en een drukdiagonaal. De onderste trekstaaf wordt onderbroken door een montageverbinding met bouten. Om het eenvoudig te houden, werken we alleen met normaalkrachten in de verbinding.

De afbeelding hierboven toont een correcte specificatie van gebalanceerde interne krachten. De resulterende normaalkrachten in de trusselementen (wederom met gebruik van een vereenvoudigde balkweergave van het model) en de trekkrachten in de bouten van de verbinding zijn als volgt. De trekkracht in de bout, inclusief wrikeffecten, is 73 kN.

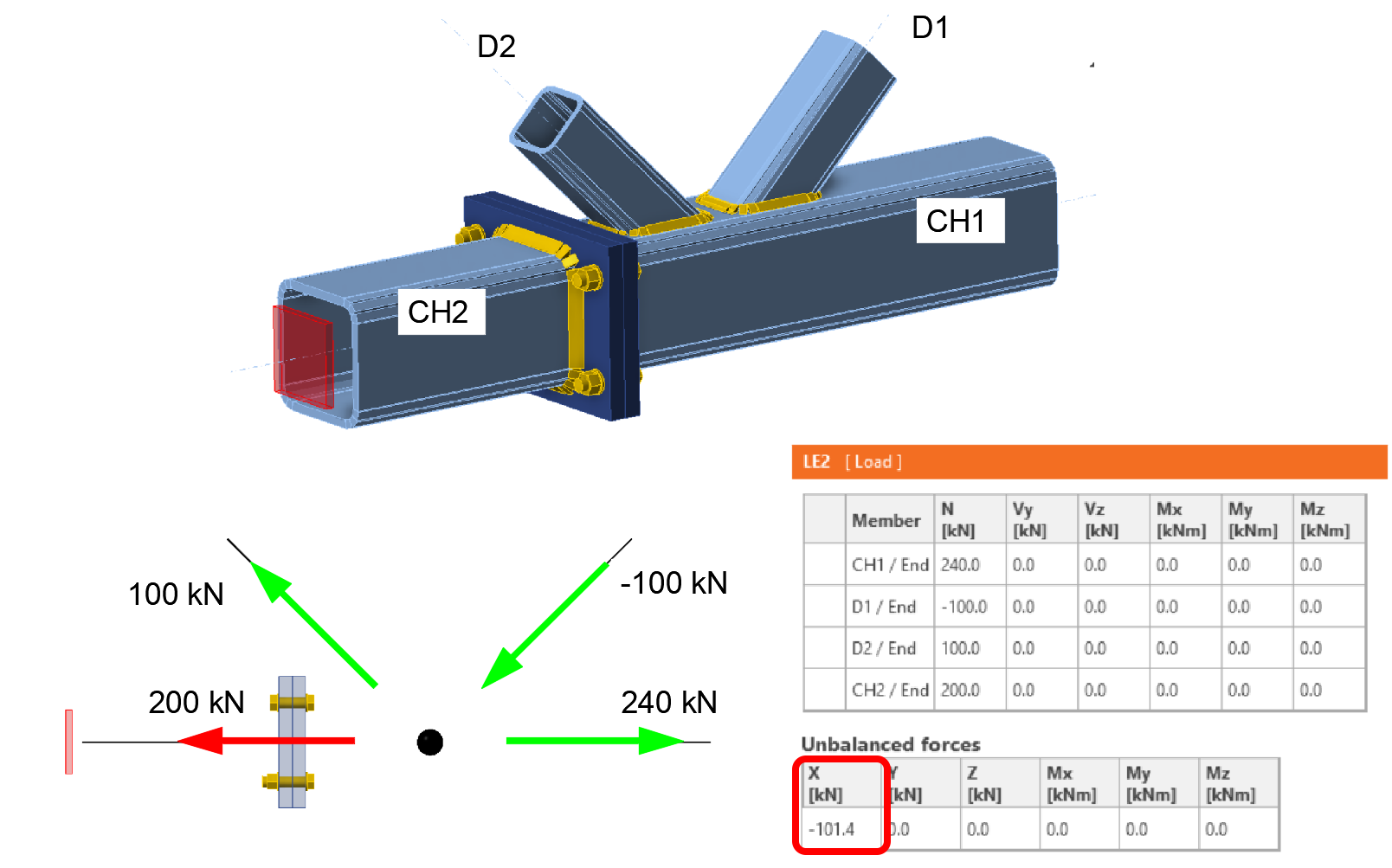
Nu zullen we dezelfde verbinding analyseren met een ongebalanceerde belasting in de horizontale richting X. De belasting op de verbinding is identiek aan het vorige voorbeeld, behalve een onjuist gespecificeerde normaalkracht van 240 kN op de onderste staaf CH1, waardoor een ongebalanceerde kracht in de X-richting van 101,4 kN ontstaat.

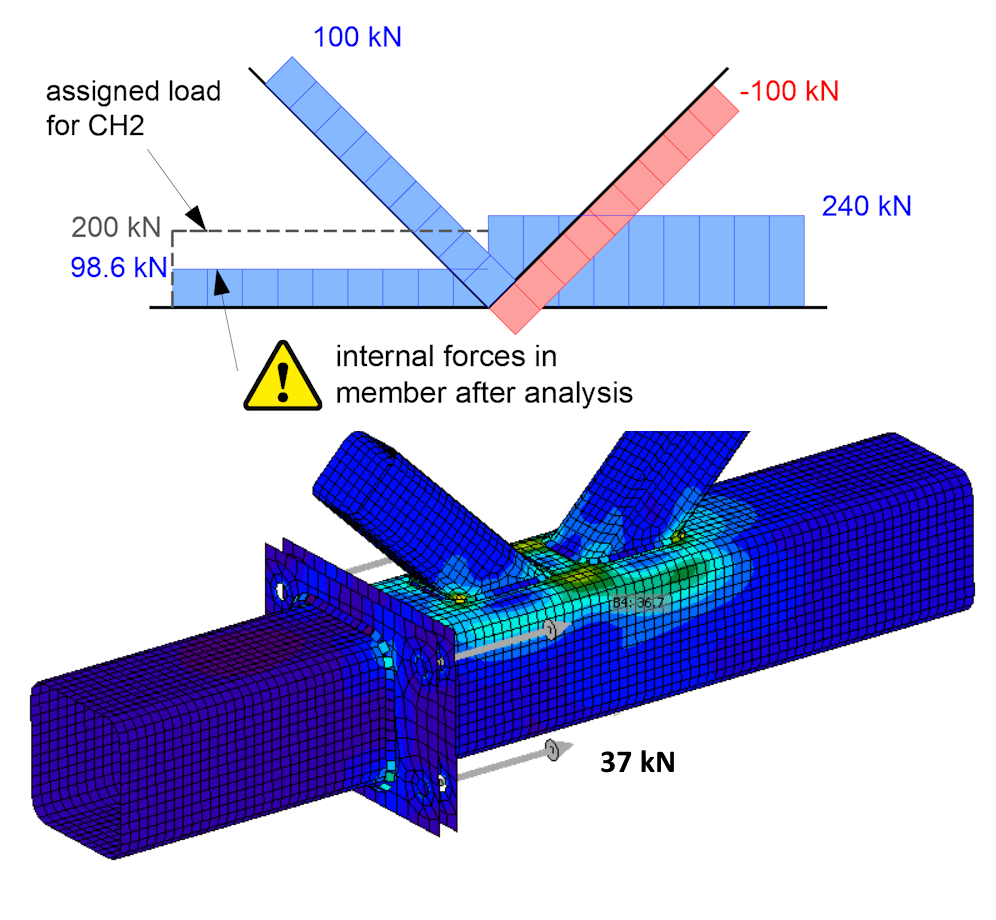
De resulterende normaalkrachten in de liggers na de berekening en de trekkrachten in de bouten zijn als volgt.

Het effect van de ongebalanceerde krachten in de verbinding in dit voorbeeld is zodanig dat het ondersteunde draagelement CH2 wordt onderworpen aan geheel andere interne krachten dan de gebruiker in de belastingstabel heeft gespecificeerd. Belangrijker is dat de boutverbinding ook gecontroleerd wordt op een aanzienlijk lagere trekkracht van 98,6 kN dan gespecificeerd in de belastingtabel. De trekkracht in de enkele bout, inclusief wrikeffecten, is 37 kN.

3 Rekenmodel met Lasten in evenwicht uitgeschakeld

Tot nu toe hebben we in de Connection-applicatie gewerkt met de functie Loads in equilibrium ingeschakeld. Nu beschrijven we de belasting en de randvoorwaarden van het rekenmodel met de functie Lasten in evenwicht uitgeschakeld.

We gebruiken opnieuw de eerder geanalyseerde horizontale balk-kolomverbinding met een geboute kopplaat. Het uitschakelen van de functie Lasten in evenwicht betekent dat het doorgaande element (kolom B1) aan beide uiteinden wordt ondersteund en dat de ongebalanceerde krachten niet worden gecontroleerd. Het is ook niet mogelijk om interne krachten op te geven in de tabel voor de dragende staaf (kolom B1). Het enige belaste element hier is de balk B2. Het rekenmodel en de belasting van de verbinding ziet er als volgt uit.

Doordat de kolom in het model aan beide zijden wordt ondersteund, wordt de dwarskracht Vz uit de ligger in de kolom opgesplitst in een trekkracht in het bovenste deel en een drukkracht in het onderste deel van de kolom. Een realistische verdeling van normaalkrachten in de kolom – waarbij de dwarskracht uit de ligger als een verticale drukkracht naar de fundering wordt overgedragen – is met dit model niet te bereiken. Evenzo sluit de momentverdeling in de kolom aan bij de gekozen ondersteuningscondities van het rekenmodel, maar weerspiegelt deze niet noodzakelijk de werkelijke interne krachtenstroom in de constructie.

Het is echter van belang dat de interne krachtverdelingen in het aangesloten en belaste element B2 niet worden beïnvloed door de statisch onbepaalde randvoorwaarden van het model. Zo blijft de beoordeling van het individuele element B2 en zijn verbinding – inclusief kopplaat, bouten en lassen – correct en representatief.

De spanningstoestand in de kolom wijkt daarentegen af van het werkelijke constructieve gedrag, met name omdat er in dit model geen belasting op wordt aangebracht. Dit onderstreept dat het uitschakelen van de functie Lasten in evenwicht een gerichte beoordeling van de verbinding van afzonderlijke staven mogelijk maakt.

Wanneer Lasten in evenwicht is ingeschakeld, kan juist de volledige verbinding worden geëvalueerd, inclusief de interactie tussen globale effecten, zoals normaalkracht en buigend moment in de kolom, en lokale effecten, zoals dwarsbuiging van de flens van een HEA-profiel bij een geboute eindplaatverbinding.