Learning Module: Load Path and Failure Modes of Fully Restrained Moment Connections

Connection design can be difficult to teach, given the detailed nature of the topic and the fundamentally three-dimensional behavior of most connections. However, connections are critically important, and lessons learned in the study of connection design, including load path and identification and evaluation of failure modes, are general and applicable to structural design broadly. IDEA StatiCa uses a rigorous nonlinear analysis model and has an easy-to-use interface with a three-dimensional display of results (e.g., deformed shape, stress, plastic strain) and thus is well suited for the exploration of the behavior of structural steel connections. Building on these strengths, a suite of guided exercises that use IDEA StatiCa as a virtual laboratory to help students learn about concepts in structural steel connection behavior and design was developed. These learning modules were primarily targeted to advanced undergraduate and graduate students but were made suitable for practicing engineers as well. The learning modules were developed by Associate Professor Mark D. Denavit from the University of Tennessee, Knoxville.

Learning Objective

After performing this exercise, the learner should be able to describe the load path for a fully restrained moment connection and identify relevant failure modes.

Background

Load Path

Loads applied to a structure are transferred through members and connections before eventually being resisted by the ground. Tracking the path of the load from its point of load application to the ground can be a helpful qualitative exercise to ensure the path is continuous, and that each component along the path has sufficient stiffness and strength. Tracking a subset of the load path through a connection provides the same benefits.

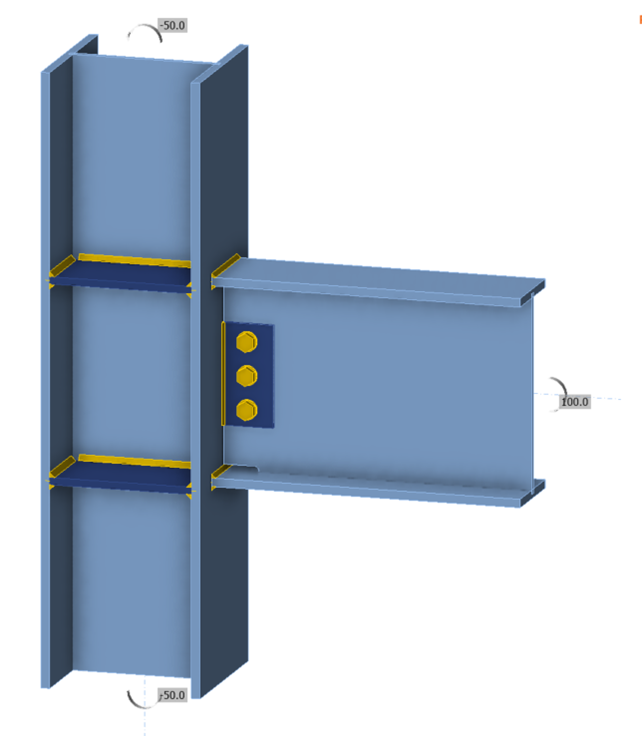
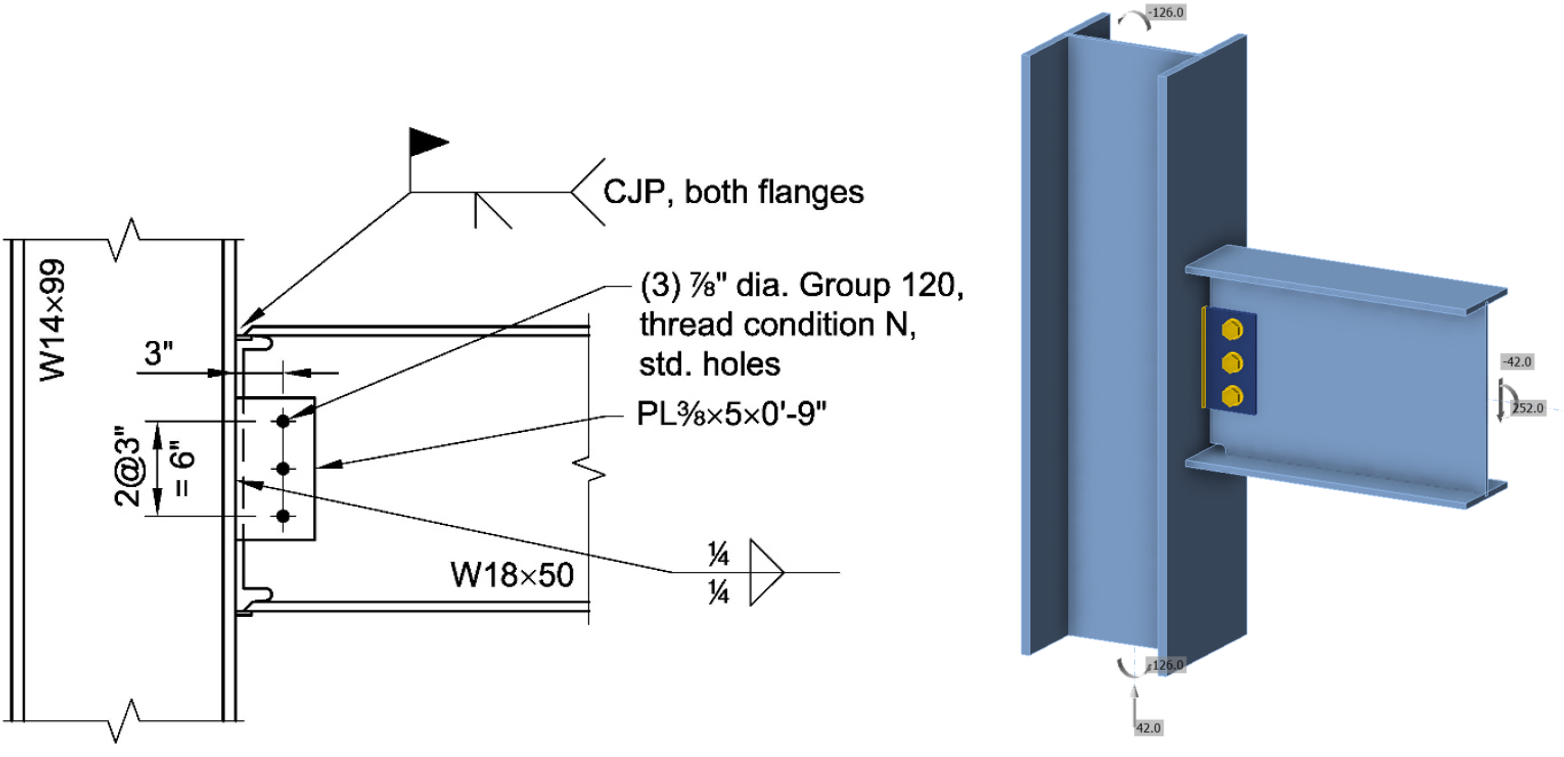
Consider, for example, the fully restrained moment connection between a wide flange steel beam and a wide flange steel column shown below. Moment in the beam is transferred to the column as follows:

• At the end of the beam, moment concentrates to the beam flanges, which are then subject to tension and compression.
• The beam flange to column flange welds transfer the beam flange forces to the column flange.
• A portion of the forces applied to the column flange are supported directly by the column while the remainder of the forces transfer through the column flange to the stiffeners.
• Force in the stiffener is transferred to the column web through shear in the stiffener to column web welds.
• The load spreads through the column cross-section, resulting in shear in the panel zone and moment in the column.

In traditional connection design, load paths such as this can help engineers develop a checklist of limit states and to ensure every step along the path has sufficient stiffness and strength. In design by inelastic analysis, load paths can help engineers by providing a mental model of connection behavior against which the results of numerical analyses can be compared.

Moment Connections

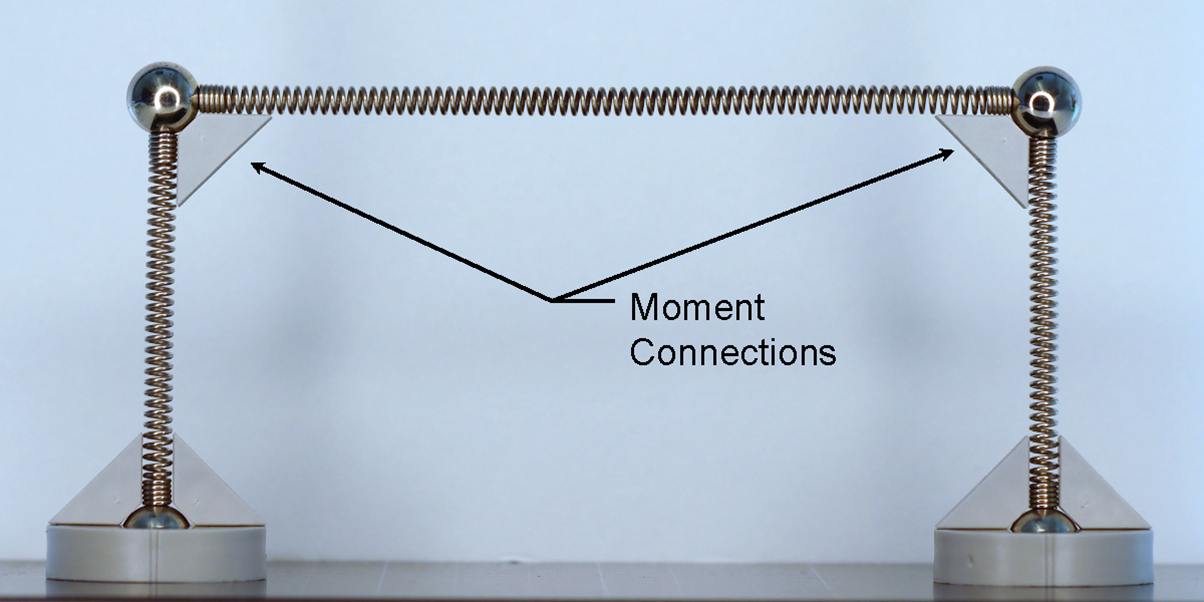
One of the major classifications of connections at the ends of beams is based on rotational stiffness. Simple shear connections are flexible enough to assume no moment is transmitted through the connection. Moment connections, on the other hand, transmit moment between the beam and column. Fully restrained connections are stiff enough to assume that no relative rotation occurs between members when transmitting the moment. Moment connections enable the beams and columns to form a moment frame that can serve as a lateral load-resisting system.

Moment frame action demonstrated with components from a (Mola Structural Kit)[ ]

Since most of the moment in a wide flange beam is resisted by the flanges, moment connections must engage the flanges of the beam directly. Moment connections typically also transfer shear or other forces from the beam to the column and thus also typically engage the web of the beam directly too. As a result, moment connections are generally statically indeterminate and the true distribution of stresses in the connection depends on the relative stiffness of the various components.

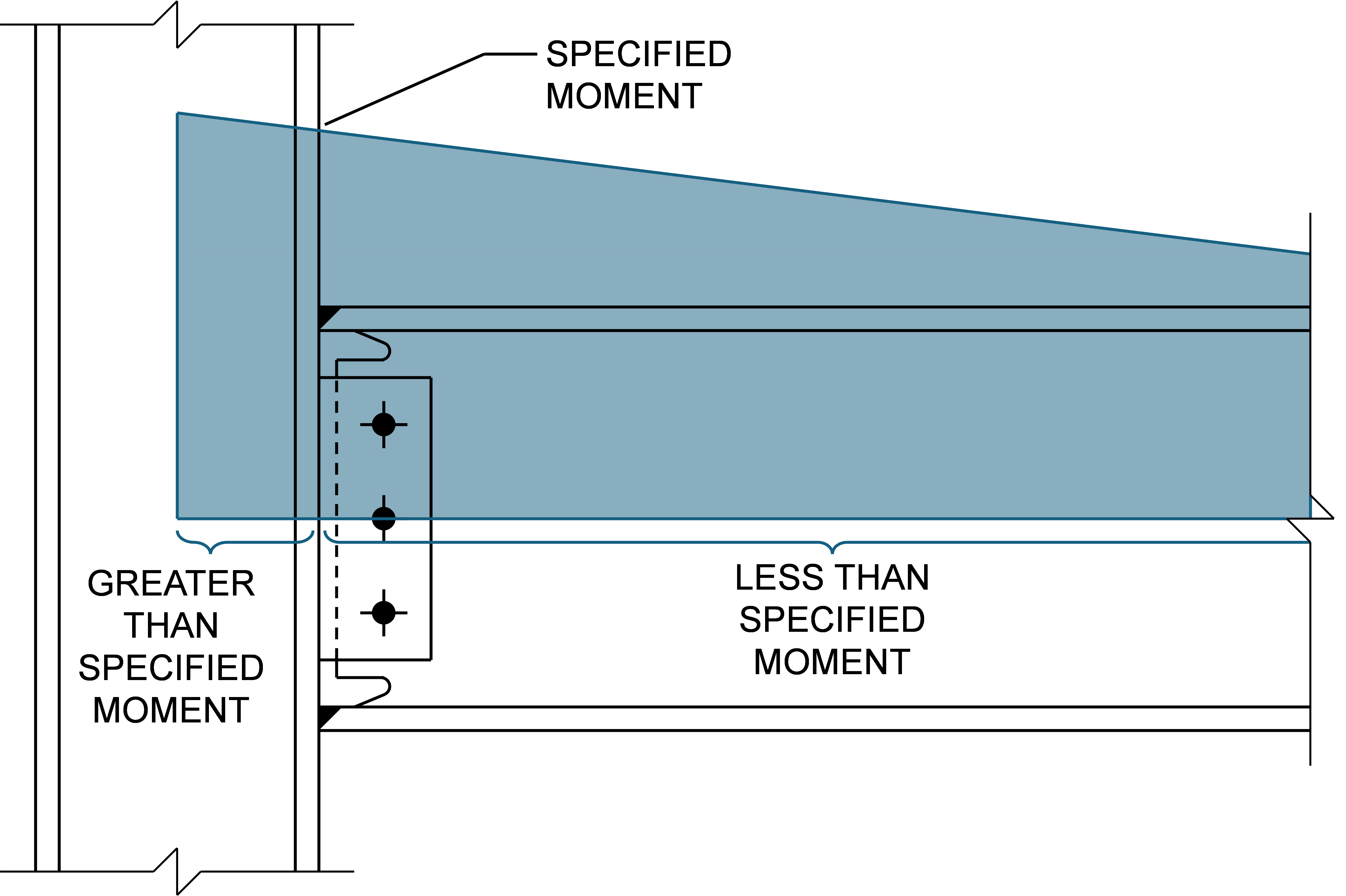
Shear forces induce a moment gradient in the beam. For moment connections, such as flange plate connections, that occur over a length of the beam, the moment is not constant. In hand calculations, the moment gradient is often conservatively neglected, and a single value of moment is used regardless of the length of the connection. The moment gradient cannot be neglected in IDEA StatiCa since the analyses ensure equilibrium and thus must be properly defined to be consistent with the structural analysis from which the required strengths were obtained. The specified moment will occur where defined by the “Forces in” option in the member menu.

In seismic design of intermediate and special moment frames, the beam-to-column connections are critical components that must be carefully designed to ensure ductility of the system. The connection must be strong enough to enable flexural yielding of the beams. The AISC standard Prequalified Connections for Special and Intermediate Steel Moment Frames for Seismic Applications (AISC 2022) describes and provides requirements for several moment connections that can achieve the desired behavior.

Connection

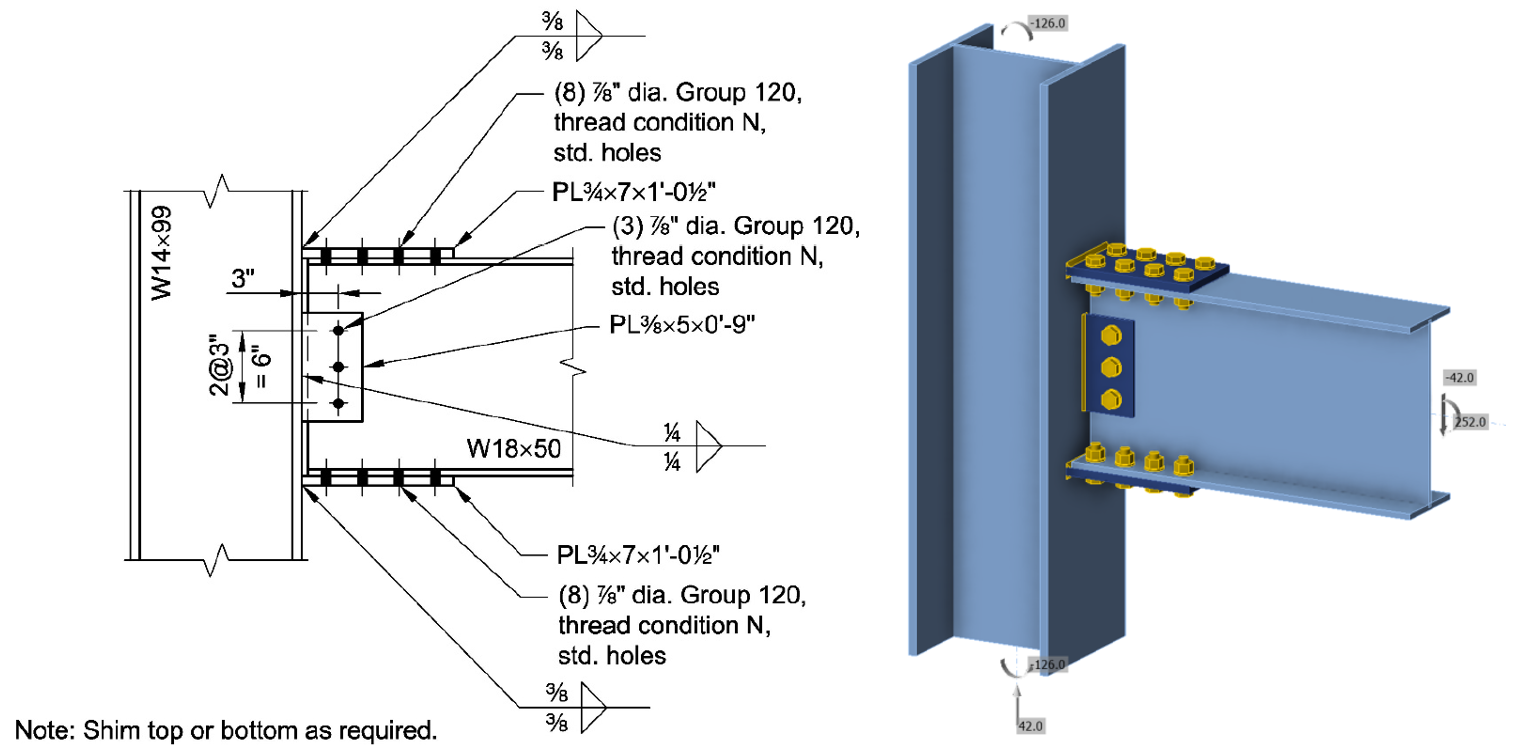
The connection examined in this exercise is based on AISC Design Examples V16.0, Example II.B-1.

This connection has a required shear strength of V_u = 42 kips and a required moment strength of M_u = 252 kip-ft, both calculated using LRFD load combinations. While not defined in the example, the specified moment is assumed to act at the face of the supporting column. For the beam member, ensure that “Forces in” is set to “Connected member face”.

Procedure

The procedure for this exercise assumes that the learner has a working knowledge of how to use IDEA StatiCa (e.g., how to navigate the software, define and edit operations, perform analyses, and look up results). Guidance for how to develop such knowledge is available on the IDEA StatiCa website.

Retrieve the IDEA StatiCa file for the example connection provided with this exercise. Open the file in IDEA StatiCa. To perform the exercise, follow the narrative, complete the tasks, and answer the questions. Note that the design example and the (Catalog of AISC limit states and design requirements) can be helpful when answering the questions.

Load Path

The load path for moment transferring from the beam to the column is as follows:

• At the end of the beam, moment concentrates in the beam flanges, which are then subject to tension and compression.
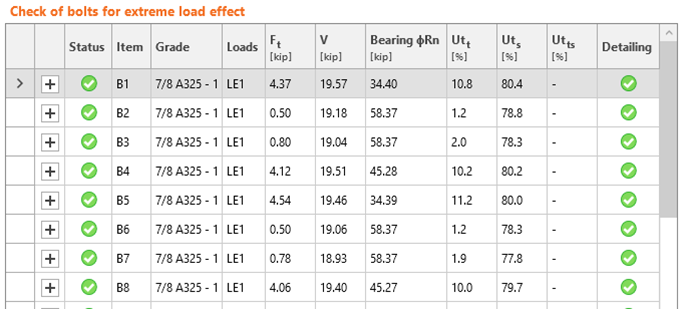
• Bolts transfer the beam flange forces to the flange plates.
• The flange plates transfer the forces from the bolt groups to the welds through axial tension or compression.
• The welds transfer the forces from the flange plates to the column flange.
• The load spreads through the column cross-section, resulting in shear in the panel zone and moment in the column.

Beam

The beam is subject to moment; therefore, limit states such as flexural yielding and lateral-torsional buckling must be investigated as part of the member evaluation. The additional limit states of tensile rupture and block shear rupture of the tension flange need to be investigated as part of the connection evaluation since there are bolt holes in the tension flange. These limit states are checked using the provisions of AISC Specification Sections F13.1 and J4.3, respectively.

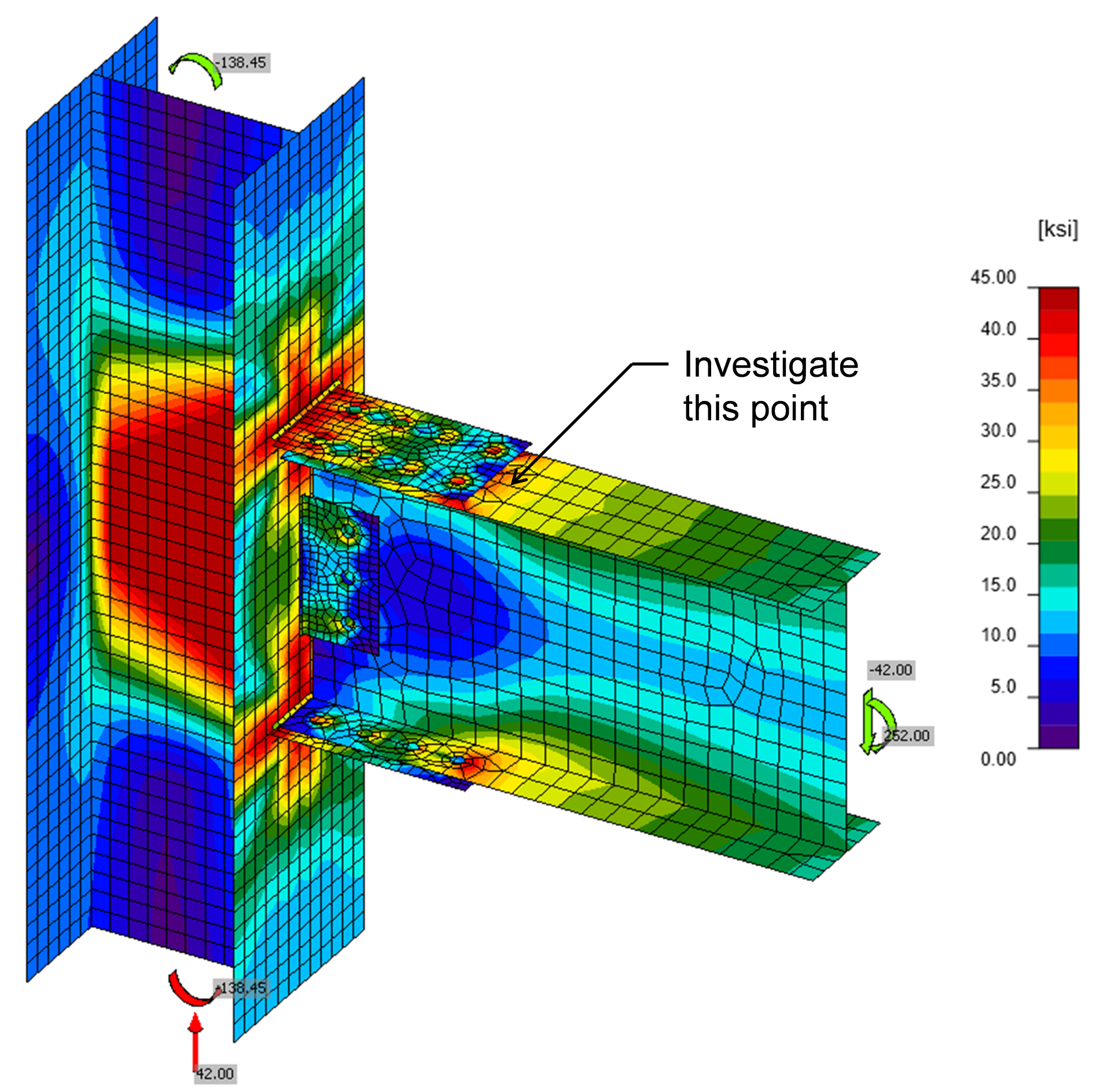
In IDEA StatiCa, these limit states are checked against the 5% plastic strain limit. Under the given loads, the beam experiences only minor amounts of plastic strain. The equivalent stress in the flanges near the end of the flange plates is approximately 30 ksi, indicated by the yellow color in the figure below.

Bolt Groups

Compare the calculated force to the IDEA StatiCa results.

The force in the bolts in the top flange in IDEA StatiCa ranges from 18.93 to 19.57 kips.

The bolt forces in IDEA StatiCa are somewhat smaller than from the hand calculations.

While it is common in design to use the moment at the face of the column to calculate the force in the bolts, using the moment at the center of the bolt group provides an answer closer to that from IDEA StatiCa. The center of the bolt group is 6.5 in. away from the face of the column. The moment in the beam at the center of the bolt group is

M = (252 kip-ft) (12 in./ft) – (42 kips) (6.5 in.) = 2,751 kip-in.

The moment arm between the bolt groups is equal to the beam depth (d = 18.0 in.). The force in each bolt group is

P = (2,751 kip-in.)/(18.0 in.) = 152.8 kips

Assuming each bolt carries the same force, the force in each bolt is

P = (152.8 kips)/8 = 19.1 kips

For each limit state, find where the results of the check are displayed in IDEA StatiCa and compare IDEA StatiCa’s calculations to your own.

Flange Plates

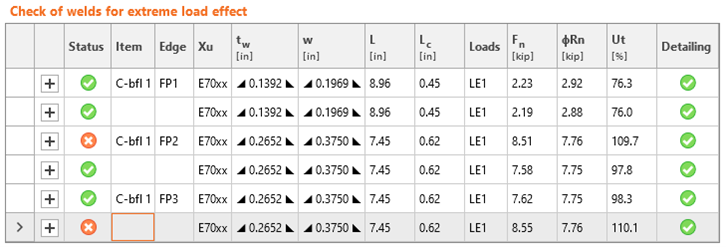
Welds

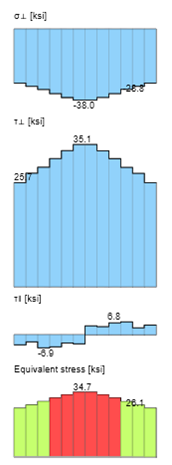
Fillet welds transfer load from the flange plates to the column flange. The required strength for the weld is the same as that for the flange plates.

In the design example using traditional calculations, the 3/8 in. fillet welds are sufficient for the applied load. In IDEA StatiCa, the 3/8 in. fillet welds are insufficient with a utilization ratio of 110%. 

What factors contribute to the difference in result?

The design strength for the controlling weld segment is ϕR_n = 7.76 kips and its length is L_c = 0.62 in, therefore the strength per length of weld is (7.76 kips)/(0.62 in.) = 12.5 kips/in. which matches the traditional calculations, meaning that the available strength is not a factor that contributes to the difference in result.

θ = 90°

w = 3/8 in.

F_EXX = 70 ksi

F_nw = 0.6F_EXX = 0.6(70 ksi) = 42 ksi

A_we = 0.707wL = 0.707(3/8 in.)L = (0.265 in.)L

k_ds = (1.0 + 0.50sin^1.5θ) = [1.0 + 0.50 sin^1.5(90°)] = 1.5

R_n = F_nwA_wek_ds = (42 ksi)(0.265 in.²)L(1.5) = (16.7 kips/in.)L

ϕR_n/L = 0.75(16.7 kips/in.) = 12.5 kips/in.

One factor that makes a difference is that the weld is assumed to be uniformly stressed in the traditional calculations whereas, in IDEA StatiCa, the weld is more highly stressed in the middle. The middle of the weld has a more direct load path that does not rely on bending of the column flange.

Another factor that makes a difference is that, in IDEA StatiCa, the welds on the outside of the connection (i.e., the top of the top flange plate and the bottom of the bottom flange plate) are more highly stressed than the welds on the inside of the connection. While this difference in stress is physically reasonable since the outside welds are farther away from the neutral axis of the beam, it is not accounted for in the traditional calculations.

Column

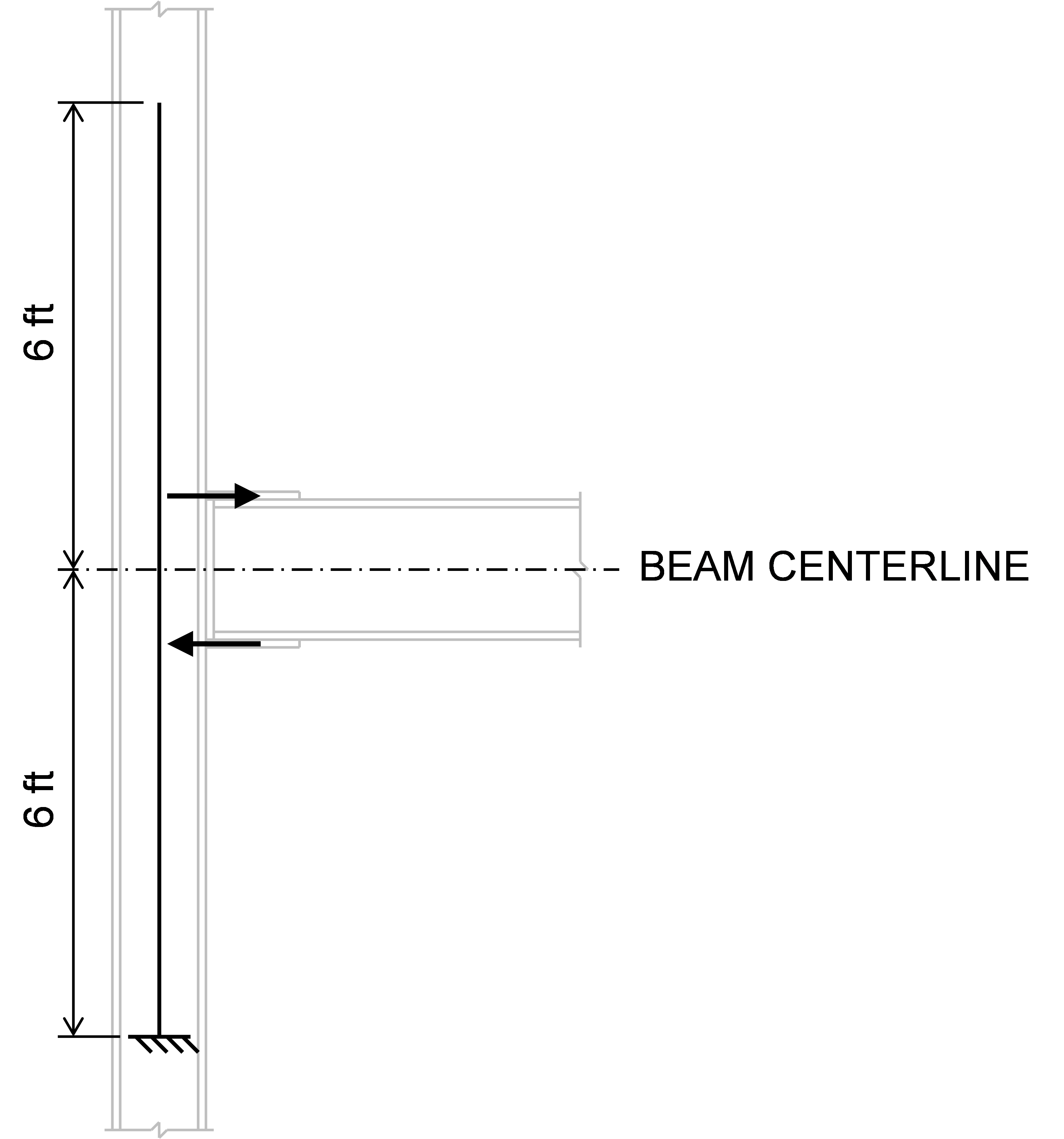
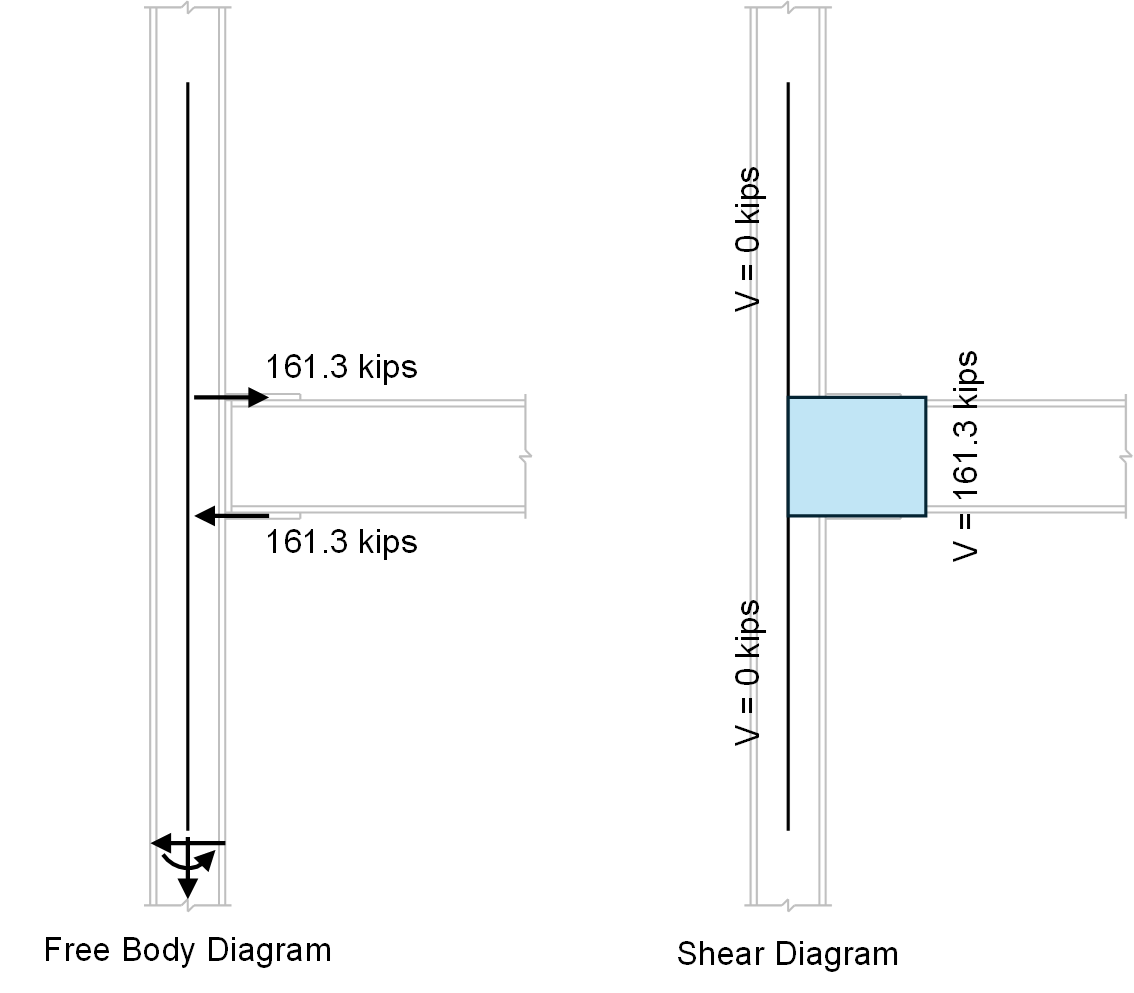
The load spreads through the column cross section, resulting in shear in the panel zone and moment in the column.

Using the simplified model shown below, draw a shear diagram for the column and check the web panel zone shear according to AISC Specification Section J10.6. Assume that the effect of inelastic panel-zone deformation on frame stability is not accounted for in the analysis. 

How is this limit state evaluated in IDEA StatiCa?

The forces in the flange plates are 161.3 kips. The distance between the applied forces is 18.0 in. + 0.75 in. = 18.75 in.

From sum of forces in the horizontal direction, the horizontal reaction at the fixed support is zero.

The required shear strength in the panel zone is R_u = 161.3 kips.

The available strength is calculated as follows, noting that this column has no required axial strength (i.e., P_r = 0 kips):

R_n = 0.60F_yd_ct_w = 0.60(50 ksi)(14.2 in.)(0.485 in.) = 206.6 kips

ϕR_n = 0.9(206.6 kips) = 185.9 kips

R_u ≤ ϕR_n, therefore the strength is sufficient.

Panel zone shear yielding is captured explicitly in the IDEA StatiCa model and limited with the 5% plastic strain limit. More information can be found here.

General Procedure

For a more open-ended experience or for connections other than the bolted flange plate moment connection, complete the following tasks:

1. Select one of the connections described below.
   • Review the design example upon which the connection is based.
   • Retrieve the IDEA StatiCa file for the connection provided with this exercise. Open the file in IDEA StatiCa.
2. Describe the load path for this connection.
3. Answer the following questions for each step in the load path:
   • What is the required strength?
   • What failure modes need to be considered?
   • How are the failure modes considered in traditional calculations?
   • How are the failure modes considered in IDEA StatiCa?

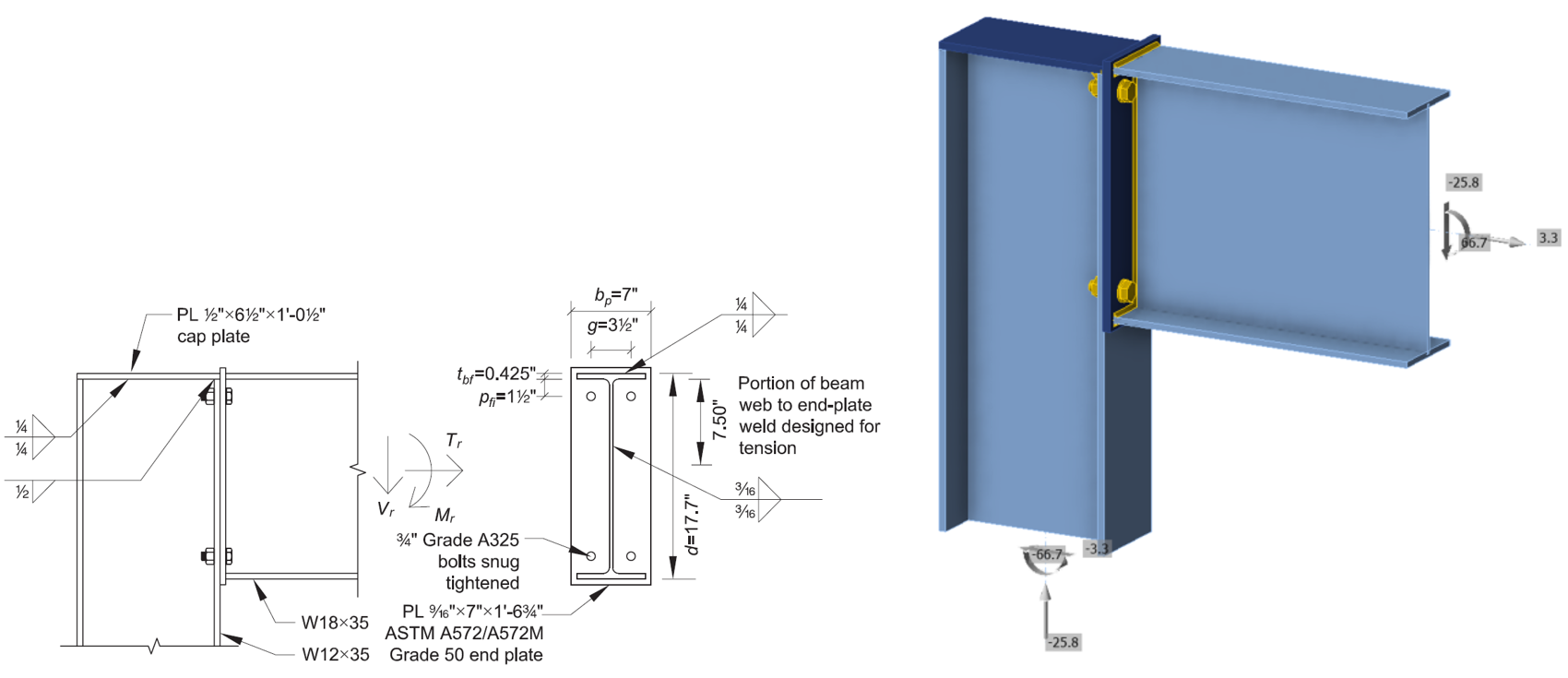
Connection 2 based on AISC Design Examples V16.0, Example II.B-3

Connection 3 based on AISC Design Guide 39, Example 5.2-1

References

AISC. (2022). Seismic Provisions for Structural Steel Buildings. American Institute of Steel Construction, Chicago, Illinois.

AISC. (2023). Companion to the AISC Steel Construction Manual, Volume 1: Design Examples, v16.0. American Institute of Steel Construction, Chicago, Illinois.

Eatherton, M. R., and Murray, T. M. (2023). End-Plate Moment Connections. Design Guide 39, American Institute of Steel Construction, Chicago, Illinois.