Smyková stěna s odstupňovanými otvory
Smyková stěna je vertikální konstrukční prvek, který odolává bočním silám, jako je vítr, zemětřesení a dalším horizontálním zatížením. Smykové stěny ztužují konstrukci, aby odolala aplikovaným zatížením a přenesla je bezpečně do základu, aniž by došlo k nadměrné deformaci, poškození nebo zřícení budovy. Smykové stěny jsou strategicky rozmístěny v půdorysu budovy, aby bylo zajištěno účinné rozložení bočních zatížení. Obvykle se umísťují po obvodu budovy nebo v blízkosti jádra budovy. Ve výškových budovách jsou smykové stěny často umístěny ve výtahových a schodišťových šachtách, aby zajistily dodatečnou tuhost a stabilitu. Smykové stěny nabízejí několik výhod, včetně zvýšené stability konstrukce, lepší odolnosti proti bočnímu zatížení a zvýšení celkové bezpečnosti při seizmických událostech. Kromě toho mohou smykové stěny přispět k architektonickému návrhu tím, že poskytují možnosti tvůrčího vyjádření a zároveň plní svou konstrukční funkci.
Popis modelu
Pro vyhodnocení výsledků byly vytvořeny čtyři ověřovací modely. Dva z těchto modelů zohledňují charakteristické vlastnosti materiálu, zatímco další dva vycházejí z návrhových hodnot podle Eurokódu 1992-1-1[3]. Tyto ověřovací modely jsou založeny na Teorii Tlakových Polí(CSFM)[1] a Druckerově-Pragerově modelu plasticity[2].
Pro lepší pochopení si prosím všimněte následující poskytnuté identifikace modelu ohledně volby materiálových vlastností:
- Detail - Charakteristické
- Detail - Návrhové
- ABAQUS - Charakteristické
- ABAQUS - Návrhové
Geometrie a materiály
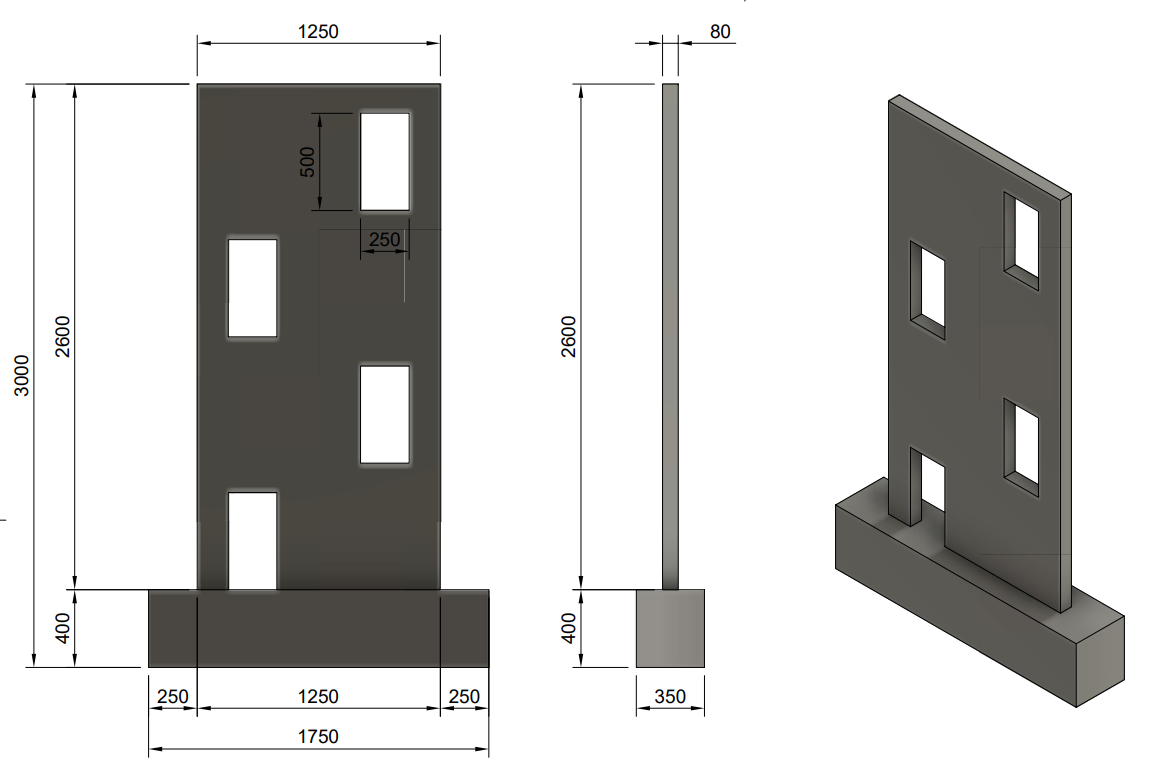
Testovací model byl oproti skutečné velikosti zmenšen čtyřnásobně. Základ konstrukce má rozměry 1750 mm x 400 mm x 350 mm, zatímco stěny mají rozměry 1250 mm x 2600 mm x 80 mm. Stěny jsou rozděleny do čtyř úrovní s odstupňovanými otvory o rozměrech 250 mm x 500 mm. Použitý beton je třídy C35/45 a je vyztužen betonářskou výztuží B500B o průměru 6 mm. Zatížení se přenáší pomocí přídavných desek z konstrukční oceli S235.
Obr. 1) Geometrie
Metoda Spojitých Tlakových Polí - CSFM
Předpoklady
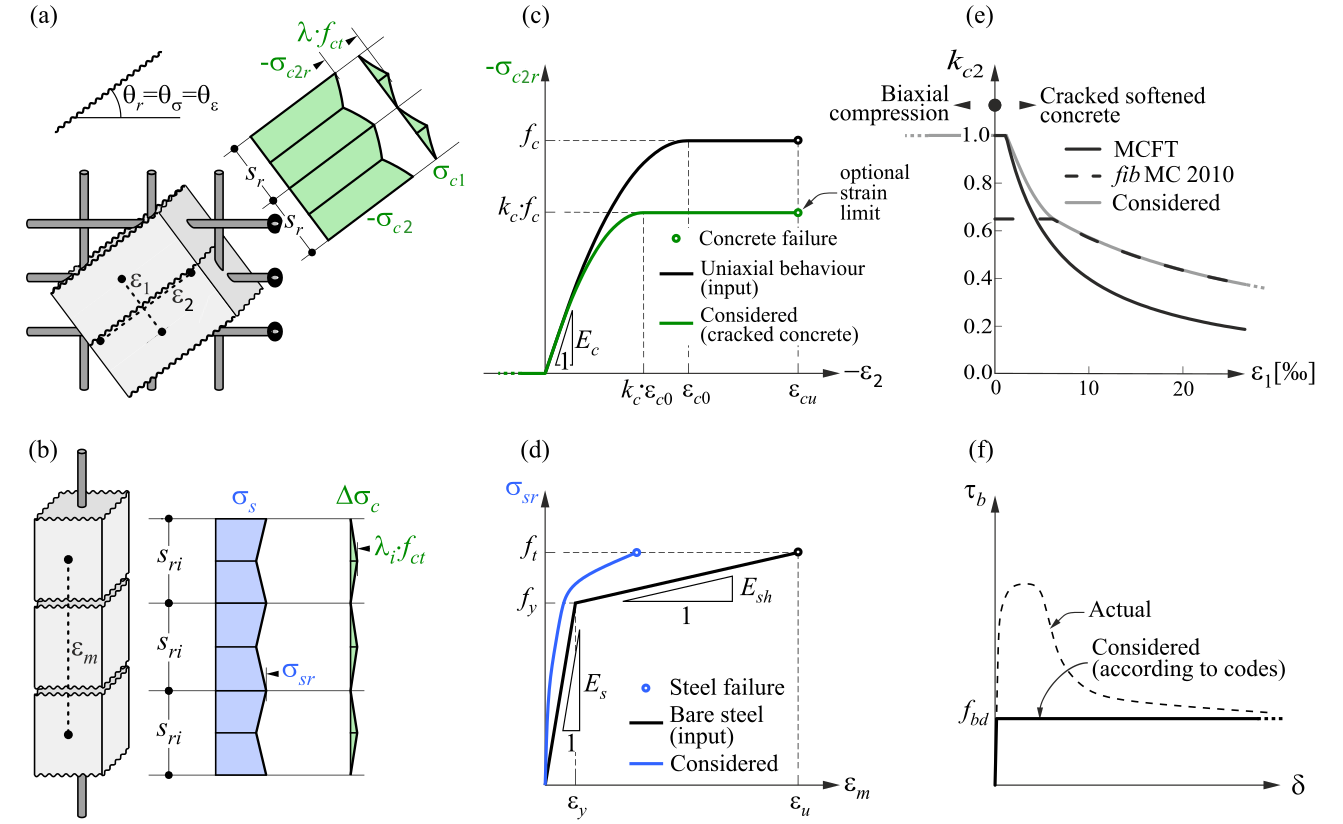
CSFM uvažuje maximální hlavní napětí betonu v tlaku (σc2r) a napětí výztuže (σsr) v trhlinách, přičemž zanedbává pevnost betonu v tahu (σc1r = 0), s výjimkou jeho ztužujícího účinku na výztuž. Zohlednění tahového ztužení umožňuje simulovat průměrné deformace výztuže (εm). Více informací o teorii lze nalézt v kapitole Teoretické podklady.
Obr. 2) Metoda kompatibilního napěťového pole - předpoklady
Drucker-Prager Plasticitní Model (DPPM)
Předpoklady
Concrete Damage Model (dále jen CDP) vychází z Drucker-Pragerovy podmínky plasticity. Tento model je vhodný pro materiály s vnitřním třením, jako je zemina nebo beton. Pevnost v tahu je menší než pevnost v tlaku a při vývoji plochy plasticity hraje roli hydrostatická část tenzoru napětí. Při obecném napětí má podmínka plasticity povrch rotačního kužele. Materiálový model pro tlaková a tahová napětí uvažuje také postkritické chování, které je řízeno tzv. parametry poškození, nabývajícími hodnot od nuly do jedné (pro téměř nulovou pružnou tuhost betonu v tlaku nebo tahu v postkritickém stavu). Čím větší je číslo parametru poškození, tím více je prvek porušen a nepřispívá k příspěvku k tuhosti.
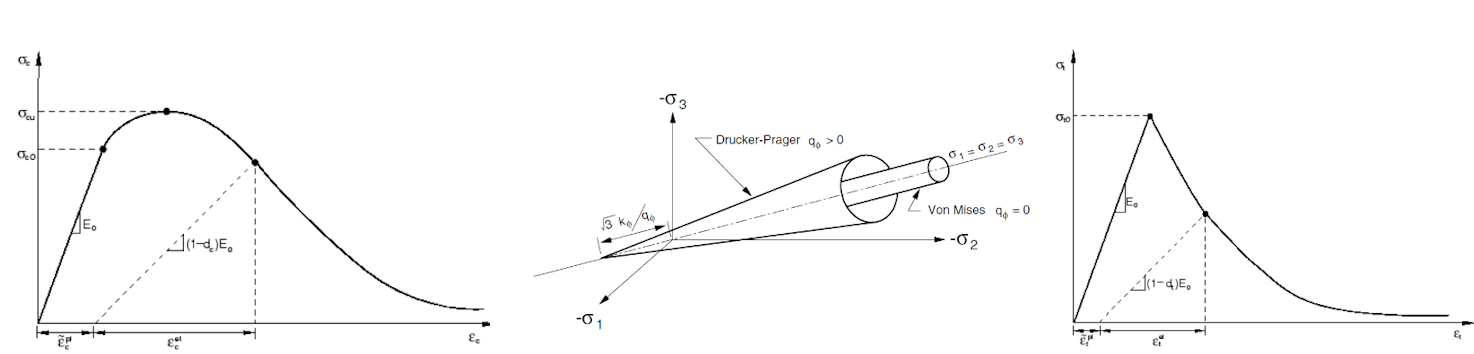
Uniaxiální materiálový model v tlaku a tahu pro beton vychází z Thorenfeldtovy teorie[4]. Všechny vstupy jsou návrhové nebo charakteristické hodnoty, které se řídí spolehlivostním přístupem podle normy EN 1992-1-1[3]. Materiálový model výztuže B500B je uvažován s tahovým ztužením.
Obr. 3) Materiálový model v tlaku (vlevo), Drucker-Pragerova plocha plasticity (uprostřed), materiálový model v tahu (vpravo).
Numerické modely
Metoda Spojitých Tlakových Polí - IDEA StatiCa Detail
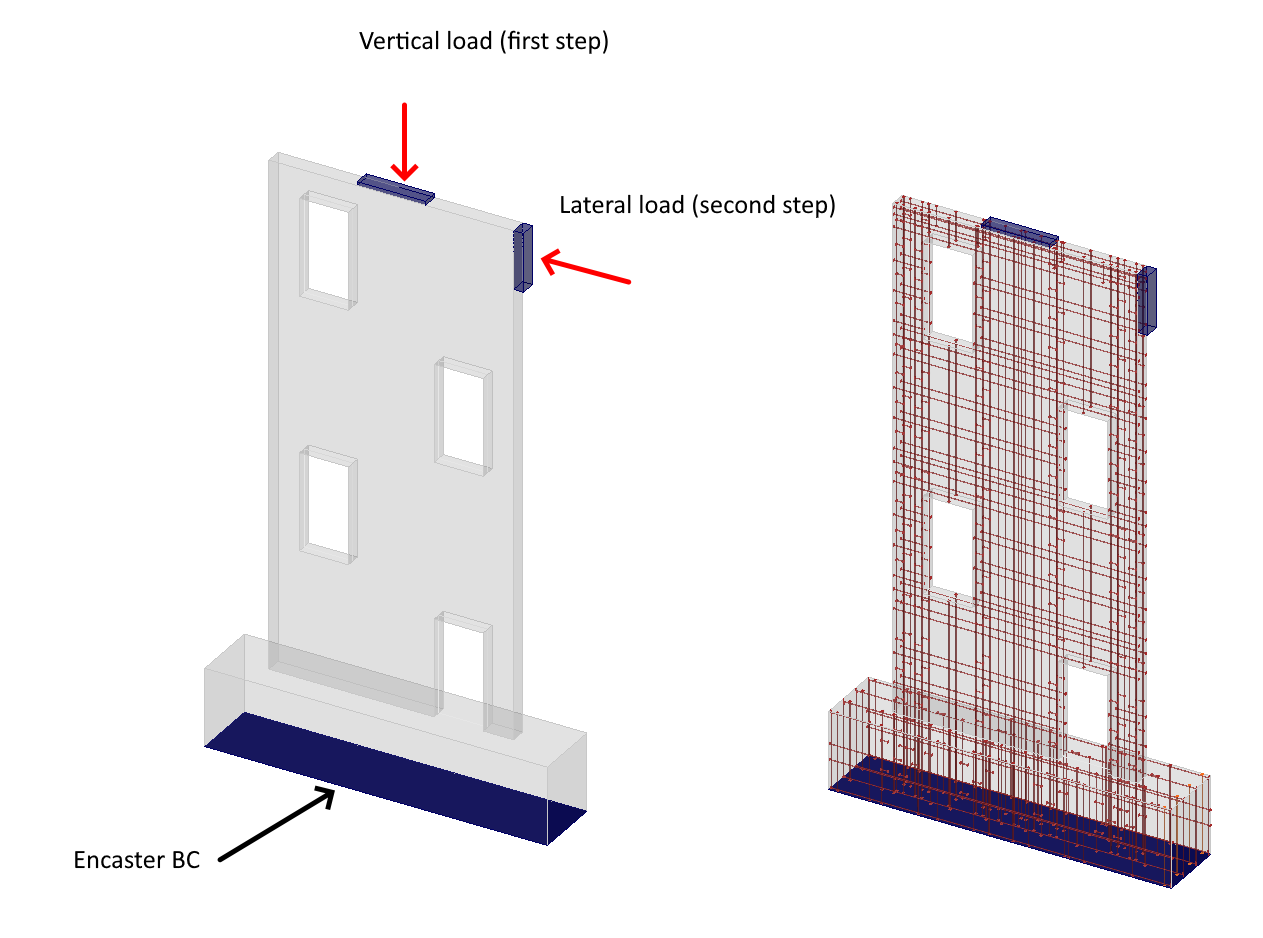
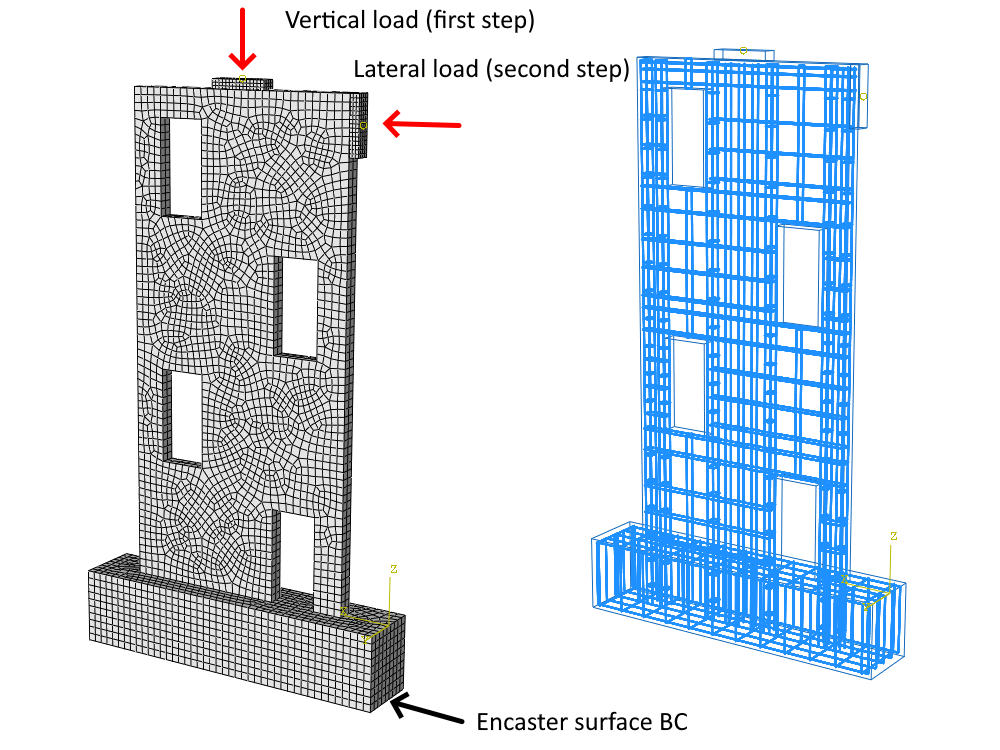
Numerický model je sestaven z 2D rovinných čtyřúhelníkových elementů, které jsou propojeny s 1D výztuží pomocí vazeb typu MPC, které zajišťují nezávislou diskretizaci jednotlivých entit betonu a výztuže. Model obsahuje dvě roznášecí zařízení v podobě ocelových desek. Horní deska o rozměrech 350 x 80 x 20 mm roznáší bodové svislé zatížení 50 kN jako první krok zatěžovacího procesu. Druhá deska z boční strany stěny o rozměrech 350 x 80 x 50 mm je využita následujícím kroku jako prvek pro přenos zatížení v rovině stěny a zajišťuje rovnoměrné rozložení bodové síly. Model uvažuje vetknutí v patě základu, omezuje stupně volnosti Tx, Tz a Ry s předpokladem 2D rovinné napjatosti pro řešení úlohy.
Obr. 4) Numerický model v programu IDEA StatiCa Detail (průběh zatěžování)
Drucker-Prager Plasticitní Model
Numerický model se skládá z 3D hexahedrálních elementů a 1D výztužných prvků, které jsou pevně svázány s prvky betonu pomocí tuhých vazeb - zajištění kompatibility přetvoření. Betonářská výztuž se skládá z prvků T3D2 přenášejících výhradně axiální účinky. Tahového změkčení betonu v postkritickém, které vede k vymazání prvku při dosažení 70% poškození v postkritickém stavu zohledňuje model soudržnost a hmoždinkový efekt. Atributy modelu a desek přesně odpovídají předpokladům CSFM.
Obr. 5) Numerický model v programu ABAQUS (průběh zatěžování).
Analýza
Přepokladem analýzy je monotónní zatěžování v horizontálním směru stěny pomocí deformačního zatížení. Nedochází tedy k cyklickému zatěžování a vytváření hysterézní křivky.
Numerické přístupy se mezi jednotlivými řešeními z hlediska analýzy mírně liší. CSFM využívá teorii malých deformací a zahrnuje materiálově nelineární analýzu (MNA). Naproti tomu model Drucker-Prager a ABAQUS využívá geometricky a materiálově nelineární analýzu a poskytuje přesnější řešení při řešení velkých deformací.
Citlivost sítě
Analýza citlivosti sítě poskytuje vhled do nesrovnalostí vyplývajících z diskretizace. Výchozí nastavení sítě uvažuje faktor jedna, což jsou čtyři elementy na nejmenší hranu v modelu s následnou diskretizací celého modelu dle tohoto pravidla. Stejná strategie byla použita pro Drucker-Prager model v programu ABAQUS.
Metoda Spojitých Tlakových Polí - IDEA StatiCa Detail
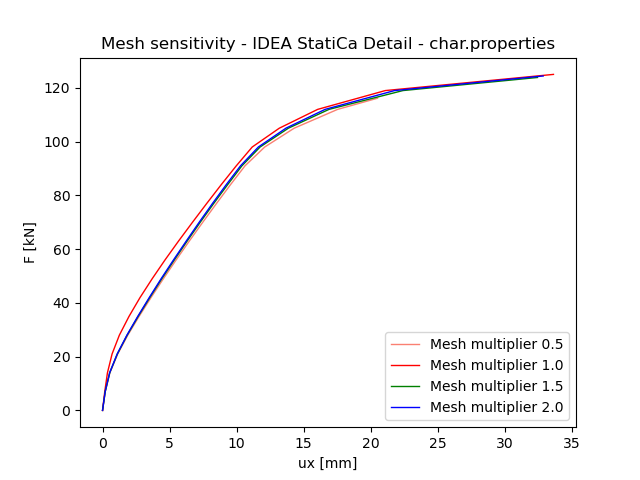
Data ukazují, že průměrná chyba mezi násobky sítě 0,5 a 2,0 je 7 %. To vede k nízké citlivosti numerického modelu na změnu velikosti sítě konečných prvků .
Obr. 6) Citlivost sítě IDEA StatiCa Detail
Drucker-Prager Plasticitní Model
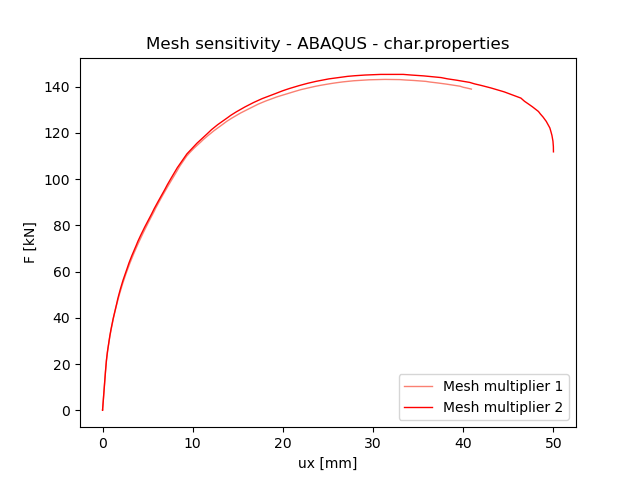
Využití 3D hexa - elementů vede při použití faktoru sítě 1,0 a 2,0 k téměř shodné síle na mezi únosnosti modelu. Rozdíl v maximální přípustné síle činí 1,3 %, což naznačuje, že řešení je velmi málo sensitivní na velikost sítě. Model pro účely analýzy uvažuje dilatační úhel 30 stupňů.
Obr. 7) Citlivost sítě ABAQUS
Výsledky
Všechny hodnoty jsou prezentovány pro faktor sítě 1,0, který byl využit jako ověřovací parametr v CSFM[1] a následně je aplikován na Drucker-Prager řešení v ABAQUS[2]. Úhel dilatace použitý na Drucker-Prager Platicitním Modelu byl nastaven na 30 stupňů. Výsledky jsou prezentovány pro charakteristické a návrhové vlastnosti materiálu, které jsou vyhodnoceny na základě Eurokódu 1992-1-1[3].
Hlavní napětí v tlaku
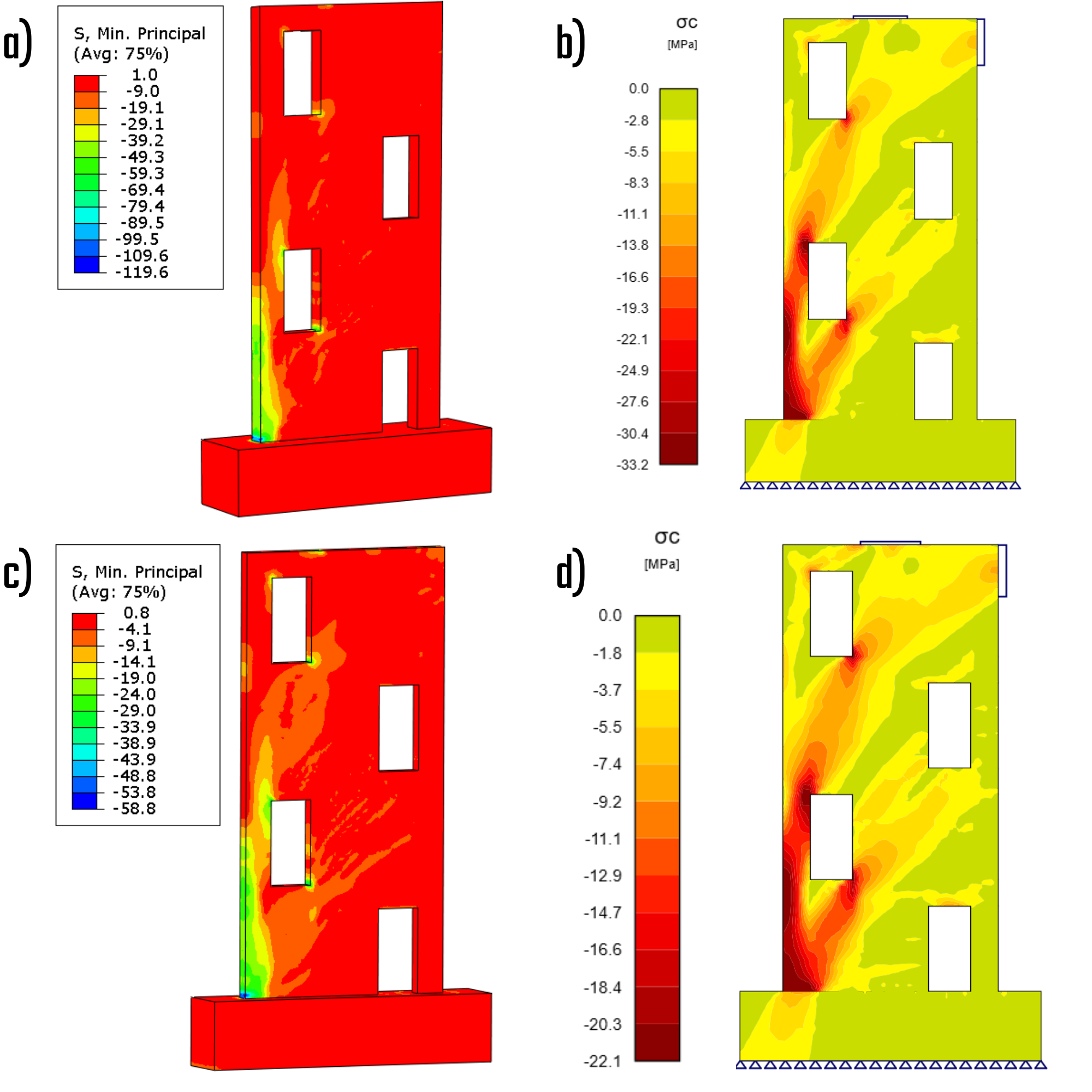
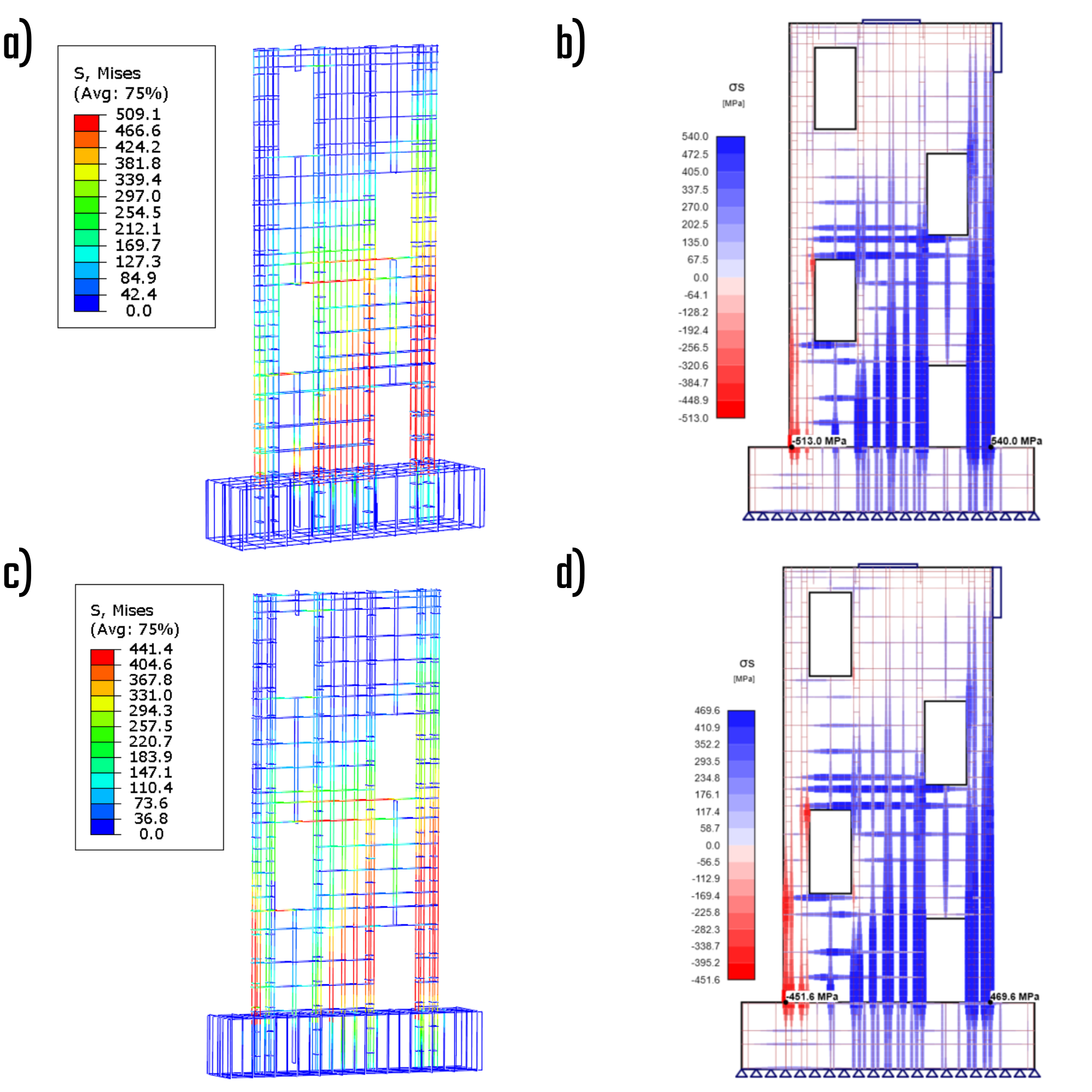
Hlavní rozdíl mezi řešením CSFM a Drucker-Prager se týká jejich přístupu k napětí. Drucker-Prager řešení zahrnuje účinek zvýšení hlavního tlakového napětí díky trojosé napjatosti, což vede obecně k vyšším hodnotám napětí, které model dokáže přenést. Naopak řešení CSFM stanovuje maximální charakteristickou nebo návrhovou uniaxiální pevnost materiálu, což usnadňuje porovnání se standardními knihovnami materiálů dle EN 1992-1-1[3]. Rozložení napětí napříč řešeními vykazují pozoruhodné rozdíly v oblastech, kde se výrazně projevuje účinek trojosé napjatosti jako je napojení stěny na základ.
Obr. 8) a) Hlavní napětí v tlaku - charakteristické (ABAQUS); b) Hlavní napětí v tlaku - charakteristické (IDEA StatiCa); c) Hlavní napětí v tlaku - návrhové (ABAQUS); d) Hlavní napětí v tlaku - návrhové (IDEA StatiCa)
Napětí ve výztužích
Napětí v betonářské výztuži vykazuje velice dobrou shodu napříč oběma metodami. Místo maximálního napětí v tlaku a v tahu se shoduje.
Obr. 9) a) Napětí v prutech - charakteristické (ABAQUS); b) Napětí v prutech - charakteristické (IDEA StatiCa); c) Napětí v prutech - návrhové (ABAQUS); d) Napětí v prutech - návrhové (IDEA StatiCa)
Deformace
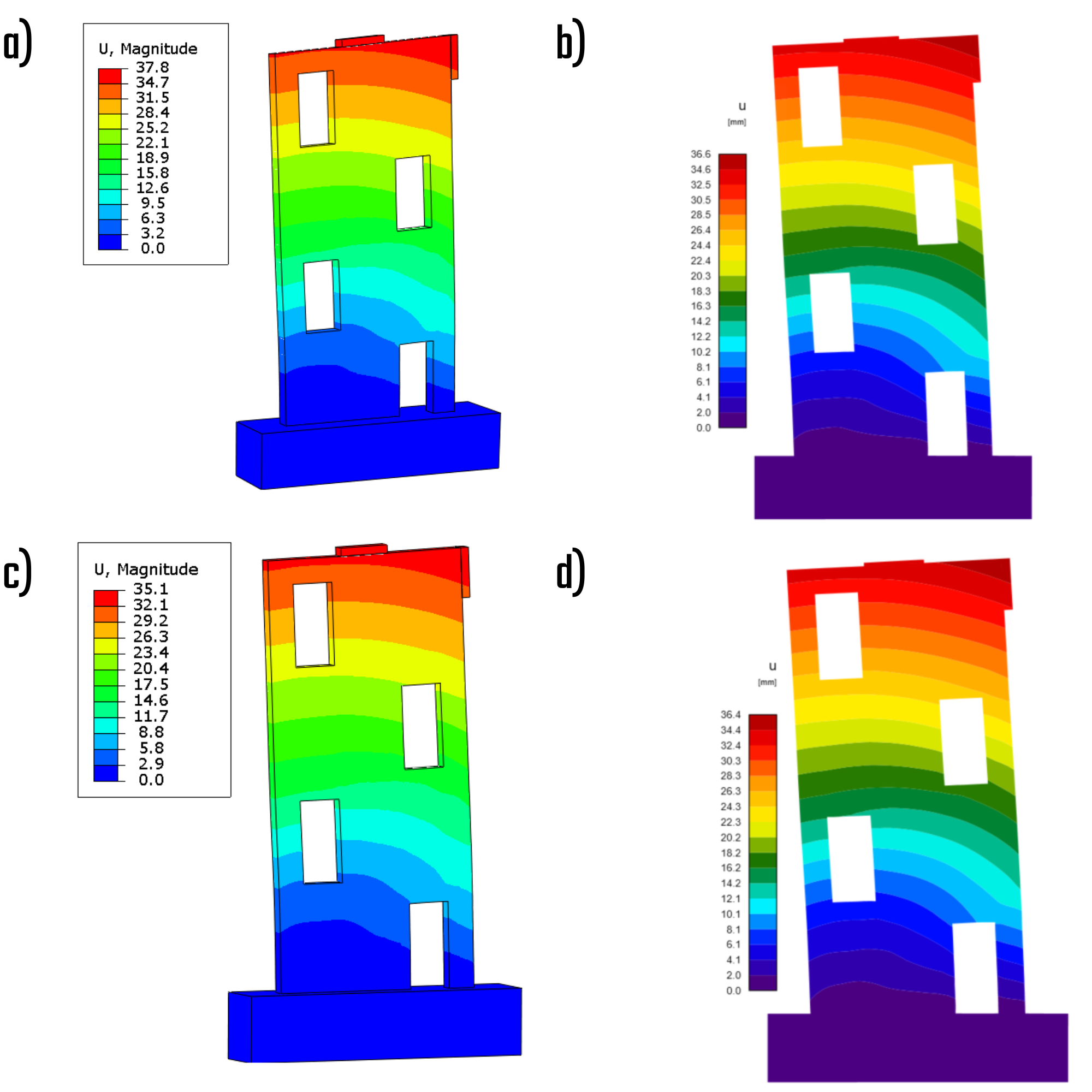
Deformace slouží jako důkaz, že geometrická nelinearita má zanedbatelné důsledky. To lze vidět z výstupu deformací pro jednotlivé metody, které dávájí téměř shodné výsledky. Z toho vyplývá, že pro daný konkrétní vzorek stěny nebude mít efekt druhého řádu vliv na chování konstrukce.
Obr. 10) a) Celkové deformace - charakteristické (ABAQUS); b) Celkové deformace - charakteristické (IDEA StatiCa); c) Celkové deformace - návrhové(ABAQUS); d) Celkové deformace - návrhové (IDEA StatiCa).
Graf závislosti síly na deformaci
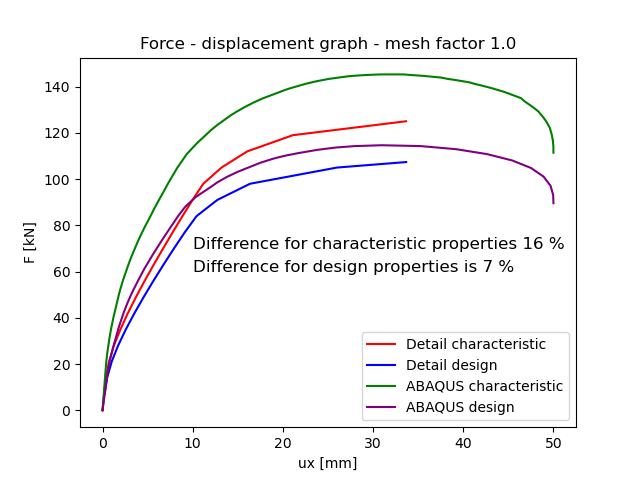
Graf představuje detailní přehled o chování modelu napříč modely pro charakteristické a návrhové materiálové parametry. Řešení CSFM vykazuje snížení únosnosti přibližně o 16 % pro charakteristické materiálové vlastnosti a 7 % pro návrhové materiálové vlastnosti oproti Drucker-Prager modelu. Tyto rozdíly vyplývají z rozdílnosti uvažování chování modelu v tahu, kde pro CSFM model je pevnost v tahu zanedbána a v modelu Drucker-Prager je uvažována.
Obr. 11) Graf závislosti síly na deformaci
Závěr
Studie zdůrazňuje klíčovou úlohu smykových stěn při odolávání bočnímu zatížení, jako jsou zemětřesení a vichřice, a tím zajišťují stabilitu a bezpečnost konstrukce. Smykové stěny, strategicky umístěné v konstrukcích budov, pomáhají rozložit boční síly, zejména ve výškových budovách, protože jsou často umístěny kolem výtahových a schodišťových šachet.
Při analýze byly použity čtyři ověřovací modely založené na charakteristických i návrhových hodnotách podle Eurokódu 1992-1-1, přičemž byla použita metoda Metoda Tlakových Polí (CSFM)[1] a Drucker-Prager Plasticitní Model (DPPM)[2]. Studie zahrnovala zmenšené modely a podrobné geometrické a materiálové specifikace s předpoklady přizpůsobenými pro každou metodu analýzy.
CSFM se zaměřila na maximální hlavní napětí v betonu a napětí ve výztuži, přičemž je zanedbána pevnost betonu v tahu s výjimkou účinků tahového ztužení. Naproti tomu DPPM zohledňovala vnitřní tření, pevnosti v tahu a tlaku a postkritické chování prostřednictvím damage parametrů.
Analýza citlivosti sítí ukázala nízkou citlivost obou metod, přičemž byly pozorovány drobné rozdíly v rozložení napětí a deformacích. Výsledky zdůraznily rozdíly v prezentaci napětí, zejména v oblasti trojosé napjastosti v DPPM, a ukázaly, že geometrická nelinearita má zanedbatelný vliv na deformace.
Grafy závislosti síly na deformaci celkově prokázaly odezvu stěny na boční zatížení, přičemž řešení CSFM vykazovala přijatelné odchylky od DPPM, což potvrzuje robustnost obou přístupů při zajišťování integrity konstrukce při působení bočních sil.
Odkazy
[1] IDEA StatiCa. (n.d.). Theoretical background for IDEA StatiCa Detail (Teoretické podklady pro IDEA StatiCa Detail). Získáno 30. května 2024 z https://www.ideastatica.com/support-center/theoretical-background-for-idea-statica-detail.
[2] Uživatelská příručka k analýze Abaqus. Uživatelská příručka k analýze Abaqus [online] www: https://classes.engineering.wustl.edu/2009/spring/mase5513/abaqus/docs/v6.6/books/usb/default.htm?startat=pt05ch18s05abm36.html.
[3] EN 1992-1-1 Eurokód 2: Navrhování betonových konstrukcí-Část I: Obecná pravidla a pravidla pro budovy. Evropský výbor pro normalizaci, 2002.
[4] Massone, L. M.; et al. Shear-Flexure Interaction for Structural Walls (Massone, L. M.; et al. Smyková interakce pro konstrukční stěny), 2006. ResearchGate. https://www. researchgate.net/publication/284079633_Shear-flexure_interaction_for_structural_walls (navštíveno 1. ledna 2006).