Modellbeschreibung

Die Biegedrill Halterung wird durch zwei Steifigkeiten simuliert, die jeder Platte hinzugefügt werden:

• Seiten (Schub) S [N] angewendet in y-Achsrichtung des lokalen Koordinatensystems der Platte
• Torsions C [Nm/m] angewendet um die x-Achse eines lokalen Koordinatensystems der Platte

Der Nutzer kann jede Platte eines Bauteils, die Länge der Halterung, den Typ (durchlaufend oder diskret mit festgelegtem Abstand) sowie Seiten- und Torsionssteifigkeiten auswählen.

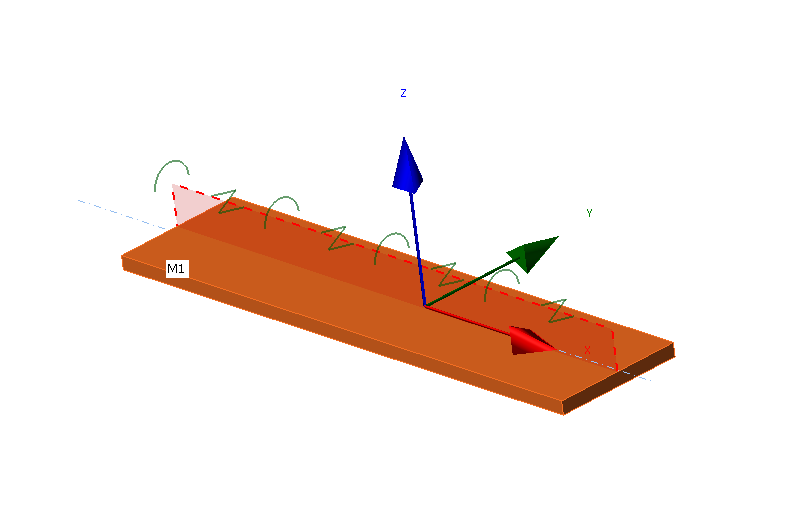
Lokales Koordinatensystem einer Platte mit aufgebrachter BDH

Knoten finiter Elemente werden entlang der Plattenbreite durch Starrkörperelemente Typ 3 (RBE3) zu einem Punkt an der Plattenlängsachse verbunden. Die Torsionssteifigkeit wird an dieser Stelle durch ein spezielles Element mit nur einer Steifigkeit aufgebracht, der Rotation um die x-Achse. Dieser Punkt ist auch durch zwei andere RBE3 mit einem speziellen Element zwischen ihnen mit einer Steifigkeit verbunden, der Verschiebung in der y-Achse.

Die Seitensteifigkeit wird vom Benutzer als frei, starr oder mit eingestellter Steifigkeit eingestellt. Die starre Steifigkeit ist ausreichend hoch und wird auf das 1000-fache der Schersteifigkeit der Platte eingestellt. Die Steifigkeit \(S\) wird pro Längeneinheit (ein Meter) mit einer Krafteinheit [N] eingestellt. Die Steifigkeit eines Elements \(S_i\) hat eine Krafteinheit geteilt durch eine Längeneinheit [N/m] und ist dann:

\[ S_i = \frac{S}{s_d} \]

Wo:

•  \(s_d\) – Abstand zwischen zwei Punkten [m]

Bei den Typ diskret wird der Abstand direkt vom Nutzer festgelegt. Für den Typ durchlaufend ist der Abstand ausreichend klein, so dass das Verhalten der Platte nicht durch den Abstand beeinflusst wird.

Ebenso wird die Torsionssteifigkeit vom Nutzer als frei, starr oder mit eingestellter Steifigkeit eingestellt. Die starre Steifigkeit ist ausreichend hoch und wird auf das 1000-fache der Biegesteifigkeit der Platte eingestellt. Die Steifigkeit \(C\) wird pro Längeneinheit (ein Meter) mit einer Einheit des Biegemoments dividiert durch die Längeneinheit [Nm/m] festgelegt. Die Steifigkeit eines Elements \(C_i\) hat eine Biegemomenteinheit dividiert durch die Längeneinheit zum Quadrat [Nm/m2] und ist dann:

\[ C_i = \frac{C}{s_d} \]

Versteckte Finite-Elemente und RBE3 sorgen für Seiten- und Torsionssteifigkeit der Bauteilplatte

Beachten Sie, dass RBE3 nur Interpolationsverbindungen sind, die selbst keine Steifigkeit bieten.

Verifizierung

Das Modell, das die BDH bereitstellt, wurde durch die Software LTBeam verifiziert, die Balkenelemente (1D) mit sieben Freiheitsgraden verwendet. Das heißt, der Querschnitt wird nicht verformt, aber das Element kann Verwölbungen aufnehmen. Der Vergleich wird am Beispiel eines IPE 180-Querschnitts aus der Stahlsorte S355 mit einer Länge von 6 m gezeigt. Der Träger wird an beiden Enden mit einer gleichmäßigen Belastung von 20 kN/m am oberen Flansch befestigt. Die Software LTBeam ist in der Lage, das elastische kritische Moment zu bestimmen, das dem Ergebnis der linearen Beulanalyse (LBA) in IDEA StatiCa Member entspricht.

Vergleich von LTBeam und IDEA StatiCa Member für Seiten- und Torsionssteifigkeit

Der kritische Lastmultiplikator zum elastischen Knicken \(\alpha_{cr}\) mit Seitensteifigkeit ist laut beiden Softwares sehr ähnlich. Die Grenze der Seitensteifigkeit, bei der das Biegedrillknicken nur bis zu 5% der Biegetragfähigkeit des Trägers wirkt, berechnet sich nach EN 1993-1-1 zu \(S_{lim} = 8589\, \textrm{kN}\). Allerdings gehen die Ergebnisse mit Torsionssteifigkeit bei höheren Rotationssteifigkeiten auseinander. Wenn Sie die verformte Form in IDEA StatiCa Member beobachten, wird der Unterschied durch die Verformung des Querschnitts verursacht, die nur durch das Schalenmodell erfasst werden kann. LTBeam bietet unrealistisch hohe Multiplikatoren für kritische Lasten für eine hohe Torsionssteifigkeit.

Um diese Behauptung zu verifizieren, wurde an der ETH Universität das Schalenelementmodell ABAQUS erstellt. Der Träger ist wieder an beiden Enden befestigt, aus Stahl der Klasse S355 und mit einer Länge von 6 m. Als Trägerquerschnitt wurde IPE 240 verwendet. Die Grenze der Torsionssteifigkeit, d.h. das Biegedrillknicken wirkt sich nur bis zu 5% der Biegesteifigkeit des Trägers aus, wurde nach \(C_{lim} = 27,13\, \textrm{kNm/m}\) berechnet. Das Modell wird durch eine Kraft in der Feldmitte am Oberflansch belastet.

Vergleich von ABAQUS, LTBeam und IDEA StatiCa Member für Torsionssteifigkeit

Der Einfluss der Torsionssteifigkeit ist bei beiden Modellen aus Schalenelementen und LTBeam divergiert sehr ähnlich. Am wichtigsten ist, dass die von GMNIA ausgegebenen Knickfestigkeiten von ABAQUS- und IDEA StatiCa Member fast übereinstimmen – die Unterschiede betragen bis zu 4 %.

Schätzen der Steifigkeit

Die BDH aus mit Beton verfüllten Decken mit Verbundwirkung aus Kopfbolzen darf bei Seitensteifigkeit als starr angenommen werden. Die Steifigkeiten von Trapezblechen oder Sandwichelementen sind viel kleiner und können durch Versuche oder Berechnungen ermittelt werden. Am häufigsten werden die Werte der Seiten- und Torsionssteifigkeit von Herstellern von Sandwichelementen oder anderen Arten von Verkleidungen empfohlen.

Die Berechnung der Seitensteifigkeit S [N] von Trapezblechen ist in EN 1993-1-3, Kapitel 10 enthalten:

\[S=1000 \sqrt{t^3} \left ( 50+10 \sqrt[3]{b_{roof}} \right ) \frac{s}{h_w} \]

Wo:

• t – Entwurfsdicke von Trapezblechen [mm]
• b_roof – Dachbreite, z.B. bei Satteldächern Abstand zwischen First und Traufe [mm]
• s – Abstand zwischen den Trägern [mm]
• h_w – Profiltiefe Trapezblech [mm] 

Die Formel gilt, wenn das Trapezblech an jeder Rippe mit dem Träger verbunden ist. Wenn die Beplankung nur an jeder zweiten Rippe mit dem Träger verbunden ist, ist S durch 0,2*S zu ersetzen.

Die Seitensteifigkeit von Sandwichelementen wird in der ECCS-Empfehlung beschrieben. Die Steifigkeit von Verbindungselementen ist von entscheidender Bedeutung:

\[S=\frac{k_v}{2B} \sum_{k=1}^{n_k}c_k^2\]

Wo:

• k_v – Schersteifigkeit eines Befestigungsmittels
• B – Breite eines Sandwichelement
• n_k – Anzahl Befestigungspaare pro Element und Lagerung
• c_k – Abstand zwischen den beiden Verbindungselementen eines Paares

Die Torsionssteifigkeit ist komplizierter und kann auch anhand der ECCS-Empfehlung geschätzt werden. Sie enthält den Beitrag von Verbindungselementen, Sandwichelementen und Trägerverzerrungen. Die Trägerverzerrung kann vernachlässigt werden, da sie bereits im Schalenelementmodell enthalten ist.

Torsions- (links) und Seitensteifigkeit (rechts) von Sandwichelementen (ECCS, 2014)

Die Bemessung nach traditionellen AISC-Methoden wird z.B. in  Denavit et al (2020) beschrieben.

Verweise

• CTICM, LTBeam v. 1.0.11, available at: https://www.cesdb.com/ltbeam.html
• Abaqus. Reference manual, version 6.16. Simulia, Dassault Systéms. France, 2016.
• EN 1993-1-3: Eurocode 3: Design of steel structures – Part 1-3: General rules – Supplementary rules for cold-formed members and sheeting, CEN, 2006.
• ECCS TC7 – Technical Working Group TWG 7.9 Sandwich Panels and Related Structures, European Recommendations on the Stabilization of Steel Structures by Sandwich Panels, 2^nd edition, 2014. ISBN 978-90-6363-081-2
• Denavit, M.D.; Jacobs, W.P.; Helwig, T.A. (2020). "Continuous Bracing Requirements for Constrained-Axis Torsional Buckling," Engineering Journal, American Institute of Steel Construction, Vol. 57, pp. 69-89.