Vincolo latero-torsionale nella progettazione strutturale

Descrizione del modello

Il Vincolo latero-torsionale è simulato da due rigidezze aggiunte a qualsiasi piastra:

• Laterale (taglio) S [N] applicato in direzione dell'asse y del sistema di coordinate locali della piastra
• Torsionale C [Nm/m] applicata intorno all'asse x del sistema di coordinate locali della piastra

Gli utenti possono selezionare qualsiasi piastra di una membratura, la lunghezza del vincolo, il tipo (continuo o discreto con distanza impostata) e le rigidezze laterali e torsionali.

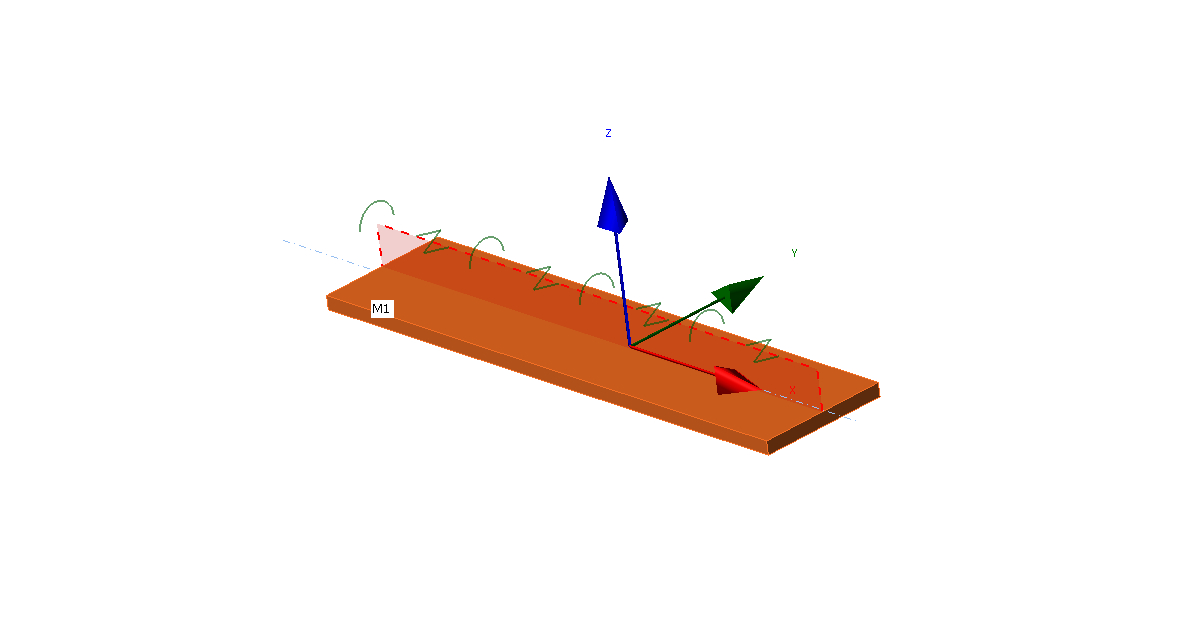
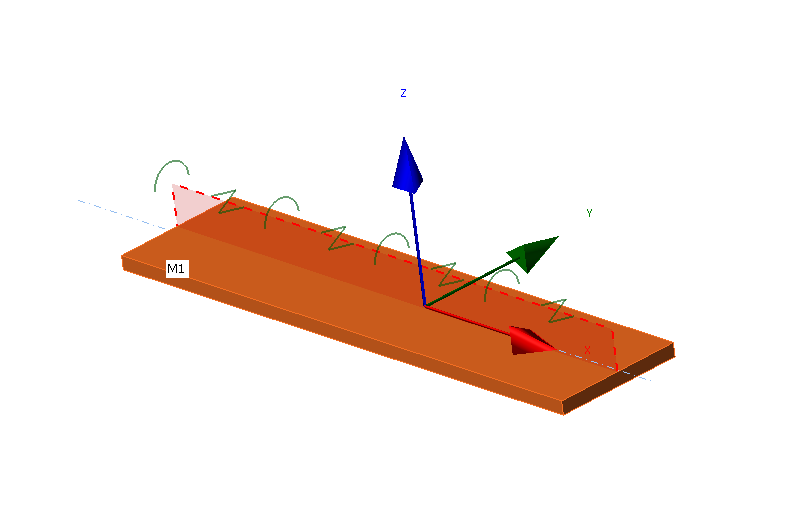
Sistema di coordinate locali di una piastra con LTR applicata

I nodi degli elementi finiti sono collegati lungo la larghezza della piastra da elementi di corpo rigido di tipo 3 (RBE3) a un punto dell'asse longitudinale della piastra. La rigidezza torsionale è applicata a questo punto da un elemento speciale a una sola rigidezza, la rotazione attorno all'asse x . Tale punto è collegato anche da altri due RBE3 con un elemento speciale tra loro a una rigidezza, lo spostamento sull'asse y . 

La rigidezza laterale può essere impostata dall'utente come libera, rigida o con rigidezza impostata. La rigidezza rigida è sufficientemente elevata, pari a 1000 volte la rigidezza a taglio della piastra. La rigidezza S è impostata per unità di lunghezza (un metro) con un'unità di forza [N]. La rigidezza di un elemento Si ha un'unità di forza divisa per l'unità di lunghezza [N/m] ed è quindi:

\[ S_i = \frac{S}{s_d} \]

dove:

•  \(s_d\) – distance between two points [m]

Per la tipologia discreta, la distanza viene impostata direttamente dall'utente. Per la tipologia continua, la distanza è sufficientemente piccola da non influenzare il comportamento della piastra.

Analogamente, la rigidezza torsionale è impostata dall'utente come libera, rigida o con rigidezza impostata. La rigidezza rigida è sufficientemente elevata, pari a 1000 volte la rigidezza flessionale della piastra. La rigidezza C è impostata per unità di lunghezza (un metro) con un'unità di misura del momento flettente diviso per l'unità di lunghezza [Nm/m]. La rigidezza di un elemento Ci ha un’unità di momento flettente diviso per l'unità di lunghezza al quadrato [Nm/m²] ed è quindi:

\[ C_i = \frac{C}{s_d} \]

Per una migliore comprensione dei valori di rigidezza, consultare il documento Raccomandazioni europee sulla stabilizzazione di strutture in acciaio con pannelli sandwich.

Gli elementi finiti nascosti e l'RBE3 forniscono la rigidezza laterale e torsionale alla piastra della membratura

Si noti che gli RBE3 sono solo links di interpolazione che non forniscono alcuna rigidezza.

Verifica

Si è verificato, tramite il software LTBeam, che si avvale di elementi a barra (1D) con sette gradi di libertà, un modello che fornisce il vincolo LRT. Ciò significa che la sezione trasversale non è deformata, ma l'elemento può essere soggetto a warping.  Il confronto è mostrato su un esempio di sezione IPE 180 in acciaio S355 lunga 6 m. La trave è fissata ad entrambe le estremità con un carico uniforme di 20 kN/m applicato all'ala superiore. Il software LTBeam è in grado di determinare il momento elastico critico che corrisponde al risultato dell'analisi di instabilità lineare (LBA) in IDEA StatiCa Member.

Confronto tra LTBeam e IDEA StatiCa Member per la rigidezza laterale e torsionale 

Il moltiplicatore di carico critico per l'instabilità elastica α_cr con rigidezza laterale è molto simile secondo entrambi i software. La rigidezza laterale limite alla quale l'instabilità latero-torsionale ha un effetto fino a solo il 5% della resistenza a flessione della trave, è calcolata secondo la norma EN 1993-1-1 come S_lim = 8 589 kN. Tuttavia, i risultati con il vincolo torsionale divergono a livelli più elevati di rigidezza rotazionale. Osservando la forma deformata in IDEA StatiCa Member, la differenza deriva dalla deformazione della sezione trasversale, la quale può essere captata solo dal modello shell. LTBeam fornisce, per una rigidezza torsionale alta, moltiplicatori di carico critico irrealisticamente elevati. 

Per verificare questa affermazione, presso l'università ETH è stato creato il modello di elementi shell ABAQUS. Anche in questo caso la trave è fissata ad entrambe le estremità, è realizzata in acciaio S355 e ha una lunghezza di 6 m. È stata utilizzata la sezione trasversale di trave IPE 240. La rigidezza torsionale limite, cioè l'instabilità latero-torsionale che ha un effetto solo fino al 5% della resistenza a flessione della trave, è stata calcolata come C_lim = 27,13 kNm/m. Il modello è sottoposto a una forza a metà della campata in corrispondenza dell'ala superiore. 

Confronto tra ABAQUS, LTBeam e IDEA StatiCa Member per la rigidezza torsionale

L'effetto della rigidezza torsionale è molto simile in entrambi i modelli costituiti da elementi shell, mentre LTBeam diverge. Soprattutto, le resistenze all'instabilità di ABAQUS e  IDEA StatiCa Member fornite dalla GMNIA quasi coincidono (le differenze sono fino al 4%).

Stima della rigidezza

Il vincolo LTR dato da solai riempiti di calcestruzzo e con azione composta data da montanti a taglio (shear studs) può essere assunto come rigido, almeno per quanto riguarda la rigidezza laterale. Le rigidezza date dalle lastre trapezoidali dei pannelli sandwich sono molto minori e possono essere determinate mediante esperimenti o calcoli. Il più delle volte, i valori di rigidezza laterale e torsionale sono raccomandati dai produttori di pannelli sandwich o di altri tipi di rivestimento. 

Il calcolo della rigidezza laterale S [N] data dalle lastre trapezoidali è riportato nella norma EN 1993-1-3, capitolo 10:

\[S=1000 \sqrt{t^3} \left ( 50+10 \sqrt[3]{b_{roof}} \right ) \frac{s}{h_w} \]

dove:

• t – spessore di progetto della lastra trapezoidale [mm]
• b_roof – larghezza del tetto, ad esempio per un tetto spiovente, è la distanza tra il colmo e una gronda [mm]
• s – distanza tra le travi [mm]
• h_w – profondità del profilo della lastra trapezoidale [mm] 

La formula è valida se la lastra trapezoidale è collegata alla trave in corrispondenza di ogni nervatura. Se la lastra è collegata alla trave solo in corrispondenza di una nervatura ogni due, allora S deve essere sostituito da 0,2 S.

La rigidezza laterale dei pannelli sandwich è descritta nella raccomandazione ECCS. La rigidezza degli elementi di fissaggio è fondamentale:

\[S=\frac{k_v}{2B} \sum_{k=1}^{n_k}c_k^2\]

dove:

• k_v – rigidezza a taglio di un elemento di fissaggio
• B - larghezza del pannello sandwich
• n_k - numero di coppie di elementi di fissaggio per pannello e supporto
• c_k - distanza tra i due elementi di fissaggio di una coppia

La rigidezza torsionale è più complessa e può essere stimata anche in base alle raccomandazioni ECCS. Contiene il contributo degli elementi di fissaggio, del pannello sandwich e della distorsione della trave. La distorsione della trave può essere trascurata perché è già inclusa nel modello degli elementi shell.

Rigidezza torsionale (a sinistra) e laterale (a destra) fornita dai pannelli sandwich (ECCS, 2014)

Nella pratica americana, il contenimento contro l'instabilità latero-torsionale è tipicamente assunto come totale o trascurabile in base al tipo e all'orientamento dell'impalcato. Ad esempio, la Tabella 8.1 del Manuale di progetto sismica AISC identifica le condizioni di vincolo per le travi soggette a compressione assiale. Tuttavia, se necessario, la rigidezza laterale può essere derivata dalla rigidezza del diaframma, G', calcolata secondo la norma AISI S310. Denavit et al. (2020) presentano un metodo di calcolo della rigidezza torsionale. 

Riferimenti

• CTICM, LTBeam v. 1.0.11, available at: https://www.cesdb.com/ltbeam.html
• Abaqus. Reference manual, versione 6.16. Simulia, Dassault Systéms. Francia, 2016.
• EN 1993-1-3: Eurocodice 3: Progettazione di strutture in acciaio - Parte 1-3: Norme generali - Norme supplementari per membrature e lamiere formate a freddo, CEN, 2006.
• ECCS TC7 - Technical Working Group TWG 7.9 Sandwich Panels and Related Structures, European Recommendations on the Stabilization of Steel Structures by Sandwich Panels, 2^a edizione, 2014. ISBN 978-90-6363-081-2
• Denavit, M.D.; Jacobs, W.P.; Helwig, T.A. (2020). "Continuous Bracing Requirements for Constrained-Axis Torsional Buckling," Engineering Journal, American Institute of Steel Construction, Vol. 57, pag. 69-89.