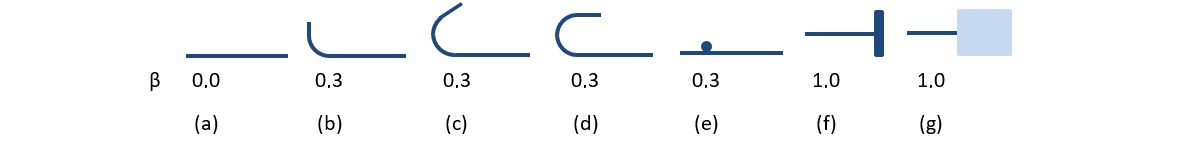Der theoretische Hintergrund basiert auf der KOMPATIBLEN SPANNUNGSFELDBEMESSUNG VON BETONBAUTEILEN (Kaufmann et al., 2020)

Bemessung von Betondiskontinuitäten in IDEA StatiCa Detail

Allgemeine Einleitung für die Bemessung von Betondetails
Bewehrungsbemessung
Finite-Elemente Implementierung
   - Auflager und Komponenten zur Lastübertragung
   - Lastübertragung an getrimmten Trägerenden
   - Geometrische Bearbeitung von Querschnitten
   - Finite-Elemente-Typen
   - Vernetzung
   - Lösungsmethode und Algorithmus zur Lastkontrolle
   - Darstellung der Ergebnisse
Strukturelementnachweis in IDEA StatiCa Detail
Überprüfung der Strukturelemente nach Eurocode
   - Materialmodelle
   - Teilsicherheitsbeiwerte
   - Analyse des Grenzzustands der Tragfähigkeit
   - Teilbelastete Flächen
   - Bemessung nach DIN EN 1992

Allgemeine Einleitung zur statischen Bemessung von Betonteilen

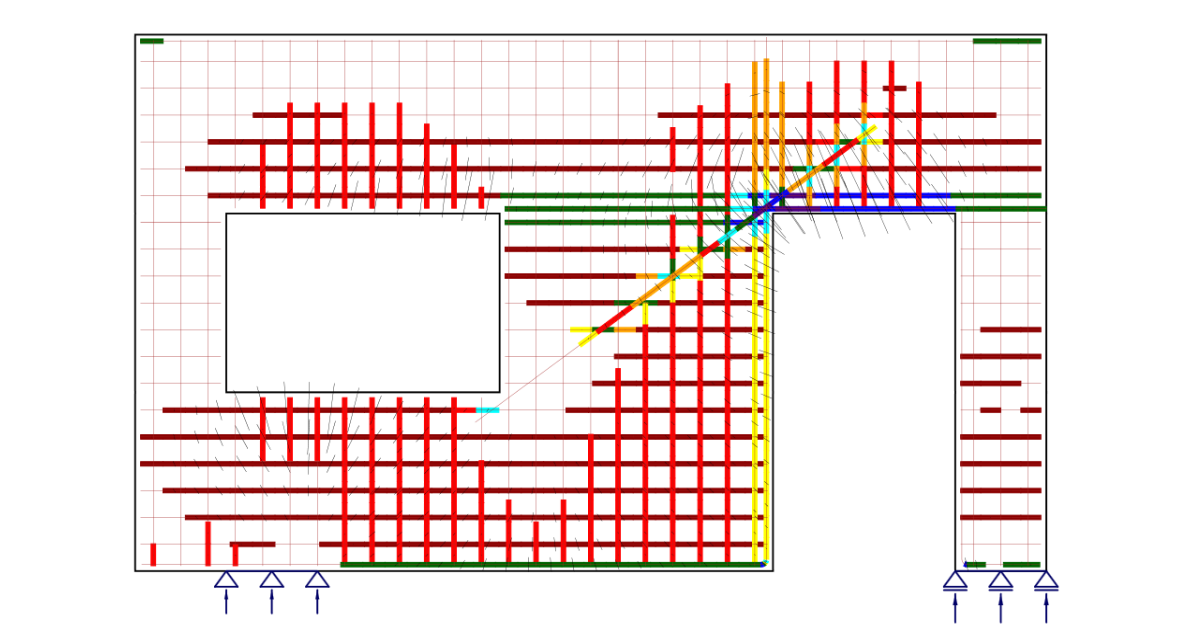
Die Bemessung von Betonbauteilen erfolgt in der Regel durch Stabelemente (1D-Elemente). Dieses Verfahren ist in allen Normen zur Tragwerksplanung beschrieben, z.B. in DIN EN 1992-1-1, und wird in der täglichen Baupraxis angewendet. Es ist jedoch nicht immer bekannt oder wird nicht beachtet, dass das Verfahren nur in den Bereichen akzeptabel ist, in denen die Bernoulli-Navier-Hypothese der ebenen Dehnungsverteilung gilt (als B-Bereiche bezeichnet). Die Stellen, an denen diese Hypothese nicht zutrifft, werden als Diskontinuitätsbereiche (D-Bereiche) bezeichnet. Beispiele für B- und D-Bereiche sind in (Abb. 1) dargestellt. Dies sind z. B. Lagerbereiche, Bereiche, in denen konzentrierte Lasten aufgebracht werden, Stellen, an denen eine abrupte Änderung des Querschnitts auftritt, Öffnungen usw. Bei der Bemessung von Betonbauwerken treffen wir auf viele andere D-Bereiche wie Wände, Konsolen, usw.

\[ \textsf{\textit{\footnotesize{Abb. 1\qquad Diskontinuitätsbereiche (Navrátil et al. 2017)}}}\]

In der Vergangenheit wurden semi-empirische Bemessungsregeln für die Dimensionierung von Diskontinuitätsbereichen verwendet. Glücklicherweise wurden diese Regeln in den letzten Jahrzehnten weitgehend durch Fachwerkmodelle (Schlaich et al., 1987) und Spannungsfelder (Marti 1985) ersetzt, die in den aktuellen Bemessungsvorschriften enthalten sind und von den Bemessenden heute häufig verwendet werden. 

Trotz der Entwicklung von Berechnungswerkzeugen in den letzten Jahrzehnten werden Fachwerkmodelle im Wesentlichen immer noch als Handberechnungen verwendet. Ihre Anwendung ist oft mühsam und zeitaufwändig, da mehrere Lastfälle berücksichtigt werden müssen. Außerdem eignet sich diese Methode nicht für den Nachweis von Gebrauchstauglichkeitskriterien (Verformungen, Rissbreiten usw.).

Das Interesse von Tragwerksplanern an einem zuverlässigen und schnellen Werkzeug zur Bemessung von D-Bereichen führte zu der Entscheidung, die neue Compatible Stress Field Method zu entwickeln, eine Methode zur computergestützten Spannungsfeldbemessung, die die automatische Bemessung von Bauteilen aus Beton unter ebener Belastung ermöglicht.

Die Compatible Stress Field Method ist eine kontinuierliche FE-basierte Spannungsfeldanalysemethode, bei der klassische Spannungsfeldlösungen durch kinematische Betrachtungen ergänzt werden. Somit kann die effektive Druckfestigkeit von Beton automatisch auf der Grundlage des Querdehnungszustands berechnet werden (Vecchio und Collins 1986; Kaufmann und Marti 1998) und der EPSF-Methode (Fernández Ruiz und Muttoni 2007). Darüber hinaus berücksichtigt das CSFM die Mitwirkung des Betons zwischen den Rissen (tension stiffening), was den Elementen realistische Steifigkeiten verleiht, und deckt alle Vorschriften der Bemessungsregeln ab (einschließlich der Aspekte der Gebrauchstauglichkeit und der Verformungskapazität), die von den bisherigen Ansätzen nicht konsequent berücksichtigt werden. Das CSFM verwendet allgemeine einachsige konstitutive Gesetze, die in den Bemessungsnormen für Beton und Bewehrung enthalten sind. Daher müssen die Planer keine zusätzlichen, oft willkürlichen Materialeigenschaften angeben, wodurch sich die Methode perfekt für die Ingenieurpraxis eignet.

Um den Einsatz von computergestützten Spannungsfeldern durch Bauingenieure zu fördern, sollten diese Methoden in benutzerfreundliche Softwareumgebungen implementiert werden. Zu diesem Zweck wurde das CSFM in IDEA StatiCa Detail implementiert, einer neuen benutzerfreundlichen kommerziellen Software, die gemeinsam von der ETH Zürich und dem Softwareunternehmen IDEA StatiCa im Rahmen des Projekts DR-Design Eurostars-10571 entwickelt wurde.

Bewehrungsbemessung

Workflow und Ziele

Das Ziel der Bemessungstools für Bewehrung in der CSFM besteht darin, den Ingenieuren dabei zu helfen, den Ort und die erforderliche Betonstahlmenge effizient zu bestimmen. Bei diesem Prozess helfen dem Benutzer die folgenden Tools: lineare Berechnung, Topologie-Optimierung und Flächen-Optimierung.

1. Tools zur Betonstahlbemessung berücksichtigen vereinfachte Werkstoffmodelle im Vergleich zu den Modellen, die für die endgültige Bemessung verwendet werden. Daher sollte dieser Schritt als Vorbemessung betrachtet werden, der während des finalen Überprüfungsschritts bestätigt werden muss. Die Verwendung von verschiedenen Tools zur Bewehrungsbemessung wird anhand des in Abb. 5 gezeigten Modells dargestellt, das den Auflager eines gevouteten Trägers darstellt, der einer gleichmäßig verteilten Last ausgesetzt ist.

\[ \textsf{\textit{\footnotesize{Fig. 5\qquad Modell zur Veranschaulichung der Verwendung der Bewehrungsentwurfswerkzeuge.}}}\]

Bewehrungsbereiche

Für Bereiche, in denen die Bewehrungsanordnung nicht im Voraus bekannt ist, stehen in der CSFM zwei Methoden zur Verfügung, mit denen der Benutzer die optimale Position der Bewehrungsstäbe bestimmen kann:

Lineare Analyse und Topologie-Optimierung. Beide Methoden bieten für einen bestimmten Lastfall einen Überblick über die Lage der Zugkräfte.

Lineare Analyse

Die lineare Analyse berücksichtigt die Eigenschaften des linearen elastischen Materials und vernachlässigt den Betonstahl. Daher ist es eine sehr schnelle Berechnung, die einen ersten Einblick in die Positionen von Zug- und Druckbereichen bietet. Ein Beispiel für eine solche Berechnung ist in Abb. 6 dargestellt.

\[ \textsf{\textit{\footnotesize{Fig. 6\qquad Ergebnisse des linearen Analysetools zur Festlegung der Bewehrungsführung}}}\]

\[ \textsf{\textit{\footnotesize{(rot: Flächen unter Druck, blau: Flächen unter Spannung).}}}\]

Topologie-Optimierung

Die Topologie-Optimierung bzw. Fachwerkanalogie ist eine Methode, mit der die optimale Materialverteilung in einem bestimmten Volumen für eine bestimmte Lastkonfiguration ermittelt werden soll. Die in IDEA StatiCa Detail implementierte Topologie-Optimierung verwendet ein lineares Finite-Elemente-Modell. Jedes finite Element kann eine relative Dichte von 0 bis 100% haben, was jeweils die relative verwendete Materialmenge darstellt; diese Elementdichten sind im Optimierungsproblem die Optimierungsparameter. Die resultierende Materialverteilung wird für die gegebenen Lasten als optimal angesehen, wenn sie die Energie der Gesamtverformung des Systems minimiert. Per Definition ist die optimale Verteilung auch die Geometrie, die für die gegebenen Lasten die größtmögliche Steifigkeit bzw. Tragfähigkeit aufweist.

Der iterative Prozess zur Optimierung beginnt mit einer homogenen Verteilung der Dichte. Die Berechnung wird für mehrere Stücke des Gesamtvolumens (20%, 40%, 60% und 80%) durchgeführt, wodurch der Benutzer das praktischste Ergebnis aus den vorgeschlagenen auswählen kann. Die resultierende Form besteht aus einem Fachwerk mit Zug- und Druckstreben und stellt die optimale Form für die gegebenen Lastfälle dar (Abb. 7).

\[ \textsf{\textit{\footnotesize{Fig. 7\qquad Ergebnisse des Entwurfswerkzeugs zur Topologieoptimierung mit 20\% und 40\% effektivem Volumen}}}\]

\[ \textsf{\textit{\footnotesize{(rot: Flächen unter Druck, blau: Flächen unter Spannung).}}}\]

3 Finite-Elemente Implementierung

3.1     Einleitung

Die CSFM berücksichtigt kontinuierliche Spannungsfelder im Beton (2D-Finite Elemente), ergänzt durch diskrete „Stab“-elemente, die die Bewehrung darstellen (1D-Finite Elemente). Daher ist die Bewehrung nicht diffus in die konkreten 2D-Finite Elemente eingebettet, sondern ausdrücklich modelliert und mit diesen verbunden. Im Berechnungsmodell wird ein ebener Spannungszustand berücksichtigt.

\[ \textsf{\textit{\footnotesize{Fig. 8\qquad Visualization of the calculation model of a structural element (trimmed beam) in Idea StatiCa Detail.}}}\]

Modelliert werden können sowohl ganze Wände und Träger als auch Details (Teile) von Trägern (isolierter Diskontinuitätsbereich, auch als zugeschnittenes Ende bezeichnet). Bei Wänden und ganzen Trägern müssen die Auflager so definiert werden, dass sich eine (äußerlich) isostatische (statisch bestimmte) oder hyperstatische (statisch unbestimmte) Struktur ergibt. Die Lastübertragung an den zugeschnittenen Trägerenden erfolgt über eine spezielle Saint-Venant-Übertragungszone (beschrieben in Abschnitt 3.3), die eine realistische Spannungsverteilung im analysierten Detailbereich gewährleistet.

3.2     Auflager und Komponenten zur Lastübertragung

Zur Modellierung der meisten Situationen während des Konstruktionsprozesses stehen in der CSFM viele Auflagertypen (Abb. 9) und Komponenten zur Lastübertragung (Abb. 10) zur Verfügung.

3.2.1   Auflager

Das Punktauflager kann auf verschiedene Arten modelliert werden, um sicherzustellen, dass die Spannungen nicht in einem Punkt lokalisiert, sondern über einen größeren Bereich verteilt werden. Die erste Option ist ein verteiltes Punktauflager (Abb. 9a), das die Last an der Bauteilkante gleichmäßig über die festgelegte Breite verteilt.

\[ \textsf{\textit{\footnotesize{Fig. 9\qquad Various types of supports:}}}\]

\[ \textsf{\textit{\footnotesize{(a) point distributed; (b) bearing plate; (c) line support; (d) patch support; (e) hanging.}}}\]

Eine Bereichslagerung dagegen (Abb. 9d) kann dagegen nur innerhalb eines Betonvolumens mit einem definierten wirksamen Radius platziert werden. Sie wird dann durch starre Elemente mit den Knoten des Bewehrungsnetzes innerhalb dieses Radius verbunden. Daher ist es erforderlich, einen Bewehrungskäfig um die Bereichslagerung herum zu definieren.

Für die genauere Modellierung einiger realer Szenarien gibt es zwei weitere Optionen für Punktauflager. Zum einen gibt es ein Punktauflager mit einer Lagerplatte mit definierter Breite und Dicke (Abb. 9b). Das Material der Lagerplatte kann festgelegt werden, und die gesamte Lagerplatte wird unabhängig vernetzt. Zum anderen steht eine hängende Lagerung zur Verfügung (Abb. 9e), mit der Transportanker oder Transportbolzen modelliert werden können.

Das Linienauflager (Abb. 9c) kann an einer Kante (durch Angabe ihrer Länge) oder innerhalb eines Elements (durch eine Polylinie) definiert werden. Ebenso ist es möglich, seine Steifigkeit und/oder sein nichtlineares Verhalten festzulegen (Auflager bei Druck/Zug oder nur bei Druck).

3.2.2   Komponenten zur Lastübertragung

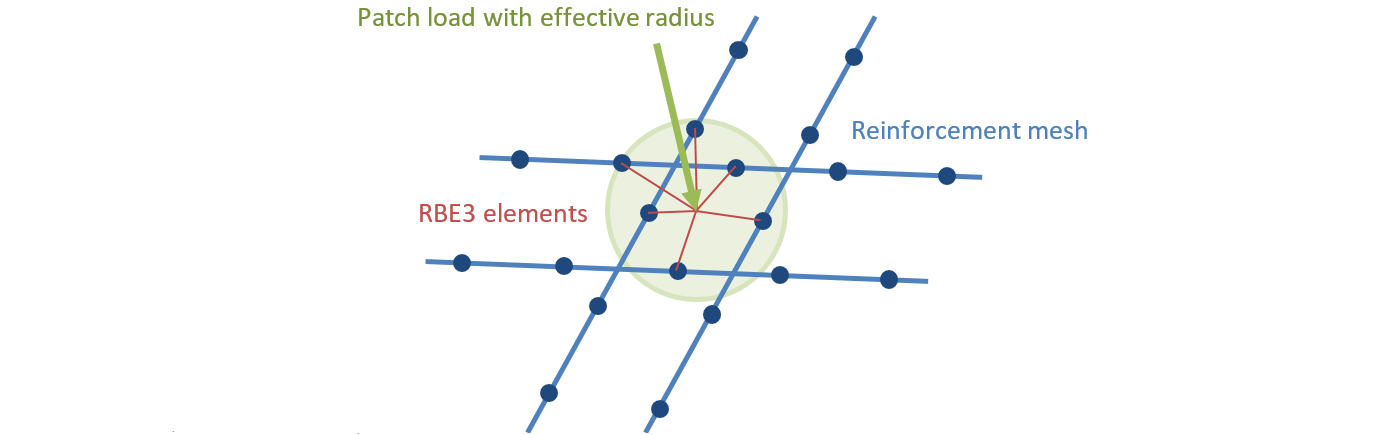
Das Einbringen von Lasten in die Struktur kann ebenfalls auf verschiedene Arten modelliert werden. Für Punktlasten kann eine Lagerplatte (Abb. 10a) ähnlich wie ein Punktauflager verwendet werden, die die konzentrierte Last über eine Stahlplatte mit festgelegter Breite und Dicke auf eine größere Fläche verteilt. Bereichslasten (Abb. 10b und Abb. 11) werden mit einem bestimmten wirksamen Radius im Beton platziert und durch starre Elemente mit den Knoten benachbarter Bewehrungsstäbe verbunden.

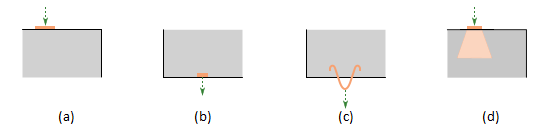
\[ \textsf{\textit{\footnotesize{Fig. 10\qquad Various types of load transfer components:}}}\]

\[ \textsf{\textit{\footnotesize{(a) bearing plate; (b) patch load; (c) hanging; (d) partially loaded area.}}}\]

Transportanker oder Transportdübel können durch eine Aufhängung modelliert werden (Abb. 10c). Der Anwender kann eine teilbelastete Fläche (Abb. 10d) verwenden, die eine Erhöhung der Tragfähigkeit von Druckbeton nach Eurocode ermöglicht (diese Komponente der Lastübertragung kann nicht verwendet werden, wenn ACI eingestellt ist). Die Struktur kann auch durch Linienlasten an den Kanten belastet werden, durch allgemeine Polylinien oder durch Flächenlasten, die z.B. das Eigengewicht darstellen (Das bei der Analyse nicht automatisch berücksichtigt wird).

\[ \textsf{\textit{\footnotesize{Fig. 11\qquad Patch load: (a) load application; (b) load transferred through rebars; (c) load transferred through concrete.}}}\]

3.3     Lastübertragung an zugeschnittenen Trägerenenden

In vielen Fällen müssen nur einige Details (Teile) eines Bauteils modelliert werden, z.B. Trägerstütze, Öffnung in der Trägermitte usw. Dieser Ansatz kann zu Auflagerkonfigurationen führen, die in IDEA StatiCa Detail instabil, aber zulässig sind (einschließlich des Falls ohne Auflager). In solchen Fällen ist es jedoch auch erforderlich, den Abschnitt zu modellieren, der die Verbindung zum angrenzenden B-Bereich darstellt, einschließlich der Schnittgrößen an diesem Abschnitt, die das Gleichgewicht erfüllen. In bestimmten Fällen (z.B. beim Modellieren der Auflager von Trägern) können diese Schnittgrößen vom Programm automatisch ermittelt werden.

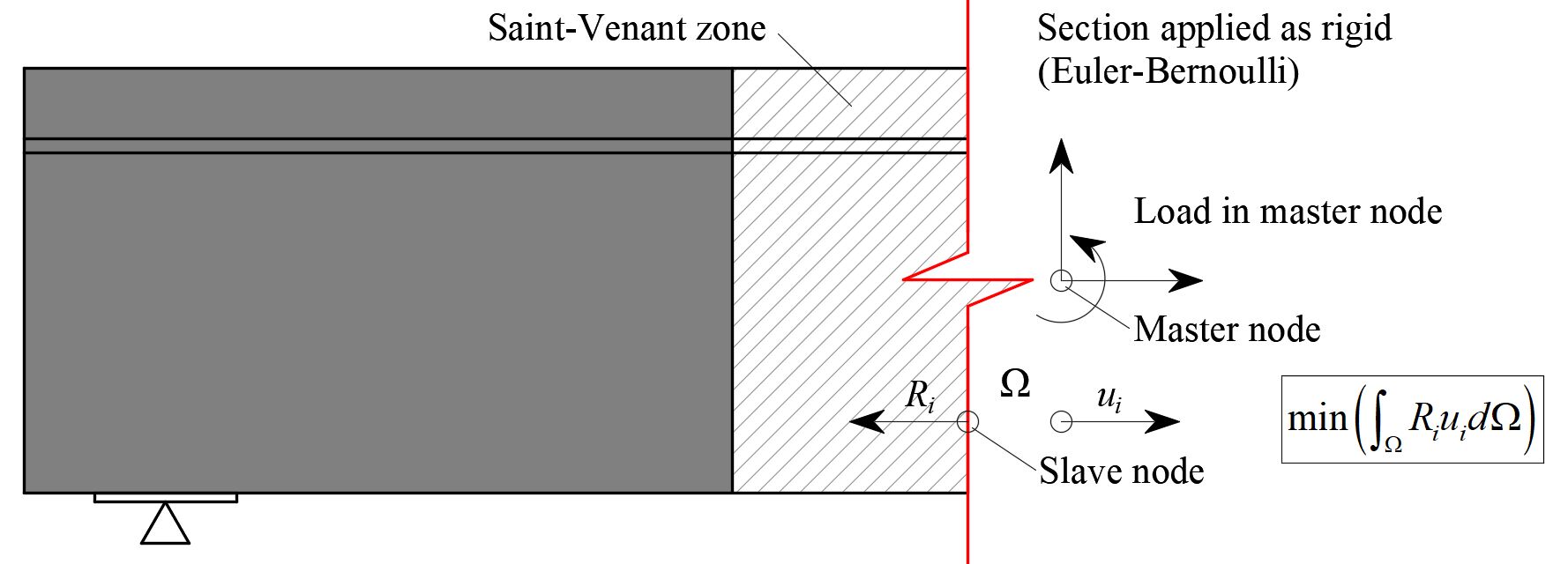
Zwischen dem B-Bereich und dem analysierten Diskontinuitätsbereich wird automatisch eine Saint-Venant-Übertragungszone erstellt, um eine realistische Spannungsverteilung im analysierten Bereich sicherzustellen. Die Breite der Übertragungszone wird als die Hälfte der Abschnittstiefe ermittelt. Da das einzige Ziel der Saint-Venant-Zone darin besteht, eine angemessene Spannungsverteilung im Rest des Modells zu erreichen, werden bei der Überprüfung keine Ergebnisse aus diesem Bereich angezeigt, und keine Stop-Kriterien werden hier berücksichtigt.

Der Rand der Saint-Venant-Zone, der das zugeschnittene Trägerende darstellt, wird als starr modelliert, d.h. es kann sich drehen, muss jedoch eben liegen. Dies geschieht durch Verbinden aller FEM-Knoten der Kante mit einem separaten Knoten in der Trägheitsmitte des Abschnitts unter Verwendung eines Starrkörperelements (RBE2). Die Schnittgrößen des Elements können dann auf diesen Knoten angewendet werden, wie in Abb. 12.

\[ \textsf{\textit{\footnotesize{Fig. 12\qquad Transfer of internal forces at a trimmed end.}}}\]

3.4     Geometrische Bearbeitung von Querschnitten

Bei Vouten-Geometrien wird die Breite der zur Modellierung der Voute verwendeten Wandelemente im Vergleich zur ursprünglichen Breite verringert, so dass sie der doppelten Höhe plus der Dicke der angrenzenden Wand entspricht. Dies basiert auf der Annahme, dass sich ein Druckspannungsfeld in einem Winkel von 45 ° von der Wand ausdehnen würde (siehe Abb. 13), so dass die zuvor erwähnte reduzierte Breite die maximale Breite wäre, die Lasten übertragen kann.

Beachten Sie, dass sich die in der CSFM implementierte Methode zur Bestimmung des wirksamen Flansches von der in 5.3.2.1 EN 1992-1-1 (2015) angegebenen Methode unterscheidet. Neben der Geometrie wird der auf Eurocode basierende, wirksame Breitenflansch deutlich von den Spannweiten und Randbedingungen einer Struktur beeinflusst.

\[ \textsf{\textit{\footnotesize{Fig. 13\qquad Width reduction of a cross-section: (a) user input; (b) FE model – automatically determined reduced flange width.}}}\]

Bei in horizontaler Ebene liegenden Vouten (Abb. 14) ist jede Voute entlang ihrer Länge in fünf Abschnitte unterteilt. Jeder dieser Abschnitte wird dann als Wand mit konstanter Dicke modelliert, die der tatsächlichen Dicke in der Mitte des jeweiligen Abschnitts entspricht.

\[ \textsf{\textit{\footnotesize{Fig. 14\qquad Horizontal haunch: (a) user input; (b)  FE model – a haunch automatically divided into five sections.}}}\]

3.5     Finite-Elemente-Typen

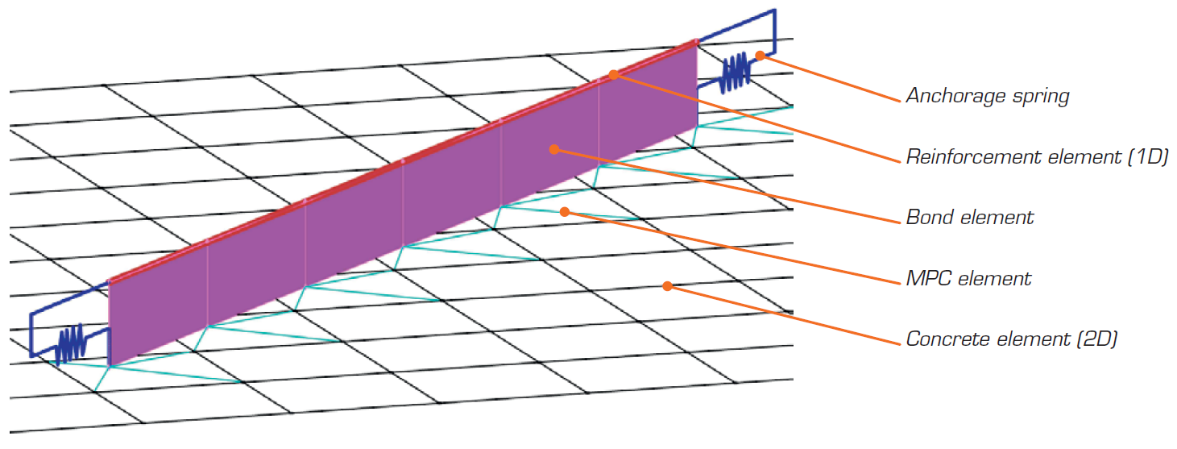
Das nichtlineare FEA-Modell wird durch verschiedene Typen von Finite-Elemente erzeugt, die zum Modellieren von Beton, Bewehrung und dem Verbund zwischen ihnen verwendet werden. Beton- und Bewehrungselemente werden zunächst unabhängig voneinander vernetzt und dann mithilfe von Mehrpunktkopplungen (MPC-Elementen) miteinander verbunden. Dadurch kann die Bewehrung eine beliebige, in Bezug zum Beton, relative Position einnehmen. Soll die Überprüfung der Verankerungslänge berechnet werden, werden Verbund- und Federelemente für das Verankerungsende zwischen der Bewehrung und den MPC-Elementen eingefügt.

\[ \textsf{\textit{\footnotesize{Fig. 15\qquad Finite element model: reinforcement elements mapped to concrete mesh using MPC elements and bond elements.}}}\]

3.5.1   Beton

Beton wird unter Verwendung der viereckigen und dreieckigen Schalenelemente CQUAD4 und CTRIA3 modelliert; diese Elemente können durch vier bzw. drei Knoten definiert sein. Es wird angenommen, dass in diesen Elementen nur ebene Spannungen vorhanden sind, d.h. Spannungen oder Dehnungen in z-Richtung werden nicht berücksichtigt

Jedes Element hat vier oder drei Integrationspunkte, die ca. 1/4 seiner Größe haben. An jedem Integrationspunkt in jedem Element werden die Richtungen der Hauptdehnungen α₁, α₃ berechnet. In beiden Richtungen werden die Hauptspannungen σ_c1, σ_c3 und die Steifigkeiten E₁, E₂ gemäß dem festgelegten Spannungs-Dehnungs-Diagramm des Betons in Abb. 2 ausgewertet. Es ist zu beachten, dass der Einfluss der Auswirkung der Druckentfestigung das Verhalten der Hauptdruckrichtung mit dem tatsächlichen Zustand der anderen Hauptrichtung gekoppelt wird.

3.5.2   Bewehrung

Bewehrungsstäbe werden durch 1D-Stabelemente (CROD) mit zwei Knoten modelliert, die nur eine axiale Steifheit aufweisen. Diese Elemente sind mit speziellen „Verbundelementen“ verbunden, die entwickelt wurden, um das Gleitverhalten zwischen einem Bewehrungsstab und dem umgebenden Beton zu modellieren. Diese Verbundelemente werden anschließend durch MPC-Elemente (Multi-Point Constraint) mit dem Netz, das den Beton darstellt, verbunden. Dieser Ansatz ermöglicht die unabhängige Vernetzung von Bewehrung und Beton, während ihre Verbindung später sichergestellt wird.

3.5.3   Überprüfung der Verankerungslänge: Verbundelemente

Die Überprüfung der Verankerungslänge erfolgt durch Implementieren der Verbundschubspannungen zwischen Betonelementen (2D) und Bewehrungsstabelementen (1D) im Finite-Elemente-Modell. Zu diesem Zweck wurde ein Finite-Elemente-Typ „Verbund“ entwickelt.

Die Definition des Verbundelements ähnelt der eines Schalenelements (CQUAD4): Es wird ebenfalls durch 4 Knoten definiert, hat jedoch im Gegensatz zu einer Schale nur eine Schersteifigkeit ungleich Null zwischen den beiden oberen und zwei unteren Knoten. Im Modell sind die oberen Knoten mit den Elementen verbunden, die die Bewehrung darstellen, und die unteren Knoten mit denen, die Beton darstellen.

Das Verhalten dieses Elements wird durch die Verbundspannung τ_b als bilineare Funktion des Schlupfes zwischen dem oberen und unteren Knoten, δ_u, beschrieben, siehe Abb. 16.

\[ \textsf{\textit{\footnotesize{Fig. 16\qquad (a) conceptual illustration of the deformation of a bond element; (b) a stress-deformation function.}}}\]

Der elastische Steifigkeitsmodul des Verbund-Schlupf-Verhältnisses G_b ist wie folgt definiert:

\[G_b = k_g \cdot \frac{E_c}{Ø}\]

wo:

k_g - Koeffizient abhängig von der Oberfläche des Bewehrungsstabs (standardmäßig k_g = 0.2)

E_c – E-Modul des Betons, angenommen als E_cm

Ø – Durchmesser des Bewehrungsstabes

Zur Überprüfung der Verankerungslänge werden die Bemessungswerte der finalen Verbundschubspannung f_bd verwendet, die in den jeweils ausgewählten Bemessungsnormen EN 1992-1-1 (2015) oder ACI 318-04 angegeben sind. Die Wiederverfestigung des plastischen Zweigs wird standardmäßig mit G_b/10⁵ berechnet.

3.5.4   Verifizierung der Verankerungslänge: Federelemente

Die Einstellung von Verankerungsenden an den Bewehrungsstäben (d.h. Biegungen, Haken, Schlaufen…), die die Vorschriften der Bemessungsnormen erfüllen, ermöglicht die Reduzierung der Grundverankerungslänge der Stäbe (l_b,net) um einen bestimmten Faktor β (im Folgenden als „Verankerungskoeffizient“ bezeichnet). Der Bemessungswert der Verankerungslänge (l_b) wird dann wie folgt berechnet:

\[l_b = \left(1 - \beta\right)l_{b,net}\]

Die verfügbaren Verankerungstypen in der CSFM umfassen einen geraden Stab (d.h. Keine Reduzierung des Ankerendes), eine Biegung, einen Haken, eine Schlaufe, einen geschweißten Querstab, einen perfekten Verbund und einen durchgehenden Stab. Diese Typen sind zusammen mit den jeweiligen Verankerungskoeffizienten β in Abb. 17 und für Längsbewehrung und in Abb. 18 für Bügel dargestellt. The values of the adopted anchorage coefficients are in accordance with EN 1992-1-1. Es ist zu beachten, dass die CSFM trotz der verschiedenen verfügbaren Optionen nur drei Arten von Verankerungsenden unterscheidet: (i) keine Verringerung der Verankerungslänge, (ii) eine Verringerung der Verankerungslänge um 30% bei normaler Verankerung und (iii) perfekter Verbund.

\[ \textsf{\textit{\footnotesize{Fig. 17\qquad  Available anchorage types and respective anchorage coefficients for longitudinal reinforcing bars in the CSFM:}}}\]

\[ \textsf{\textit{\footnotesize{(a) straight bar; (b) bend; (c) hook; (d) loop; (e) welded transverse bar; (f) perfect bond; (g) continuous bar.}}}\]

\[ \textsf{\textit{\footnotesize{Fig. 18\qquad  Available anchorage types and respective anchorage coefficients for stirrups.}}}\]

\[ \textsf{\textit{\footnotesize{Closed stirrups: (a) hook; (b) bend; (c) overlap. Open stirrups: (d) hook; (e) continuous bar.}}}\]

Die beabsichtigte Reduzierung von l_b,net  entspricht der Aktivierung des Bewehrungsstabs an seinem Ende bei einem Prozentsatz seiner maximalen Kapazität, der durch den Koeffizienten der Verankerungsreduktion gegeben ist, wie in Abb. 19a gezeigt.

\[ \textsf{\textit{\footnotesize{Fig. 19\qquad  Model for the reduction of the anchorage length:}}}\]

\[ \textsf{\textit{\footnotesize{(a) anchorage force along the anchorage length of the reinforcing bar; (b) slip-anchorage force constitutive relationship.}}}\]

Die Verringerung der Verankerungslänge ist im Finite-Elemente-Modell durch ein Federelement am Stabende (Abb. 15) enthalten, das durch das in Abb. 19b dargestellte Werkstoffmodell definiert ist. Die maximale Kraft, die von dieser Feder übertragen wird (F_au), ist definiert durch:

\[F_{au} = \beta \cdot A_s \cdot f_{yd}\]

wo:

β – Verankerungsfaktor, basierend auf dem Verankerungstyp

A_s – Querschnitt des Bewehrungsstabes

f_yd – Bemessungswert der Streckgrenze der Bewehrung.

3.6     Vernetzung

Die im vorherigen Kapitel beschriebenen finiten Elemente werden intern implementiert, und das Analysemodell wird automatisch generiert, ohne dass eine erfahrene Interaktion durch den Anwender erforderlich ist. Ein wichtiger Teil dieses Prozesses ist die Vernetzung.

3.6.1   Beton

Alle Betonbauteile sind miteinander vernetzt. Von der Anwendung wird eine empfohlene Elementgröße automatisch, basierend auf der Größe und Form der Struktur und unter Berücksichtigung des Durchmessers des größten Bewehrungsstabes, berechnet. Darüber hinaus garantiert die empfohlene Elementgröße, dass mindestens 4 Elemente in dünnen Teilen der Struktur. wie schlanken Stützen oder dünnen Platten, erzeugt werden, um zuverlässige Ergebnisse in diesen Bereichen zu gewährleisten. Die maximale Anzahl von Betonelementen ist auf 5000 begrenzt, dieser Wert reicht jedoch aus, um die empfohlene Elementgröße für die meisten Strukturen bereitzustellen. Anwender können jederzeit eine benutzerdefinierte Betonelementgröße auswählen, indem sie den Multiplikator der Standard-Netzgröße ändern.

3.6.2   Bewehrung

Die Bewehrung ist in Elemente unterteilt, die in etwa der Länge der Größe der Betonelemente entsprechen. Sobald die Bewehrungs- und Betonnetze erzeugt sind, werden sie mit Verbundelementen (GZT) oder direkt durch MPC-Elemente (GZG) verbunden, wie in Abb. 15 gezeigt.

3.6.3   Lagerplatten

Hilfsbauteile, wie Lagerplatten, sind unabhängig voneinander vernetzt. Die Größe dieser Elemente wird mit 2/3 der Größe der Betonelemente im Verbindungsbereich berechnet.  Die Knoten des Netzes für die Lagerplatte werden dann unter Verwendung von Interpolationskopplungselementen (RBE3) mit den Randknoten des Betonnetzes verbunden.

3.6.4   Lasten und Auflager

Bereichslasten und Bereichslager werden nur mit der Bewehrung verbunden, wie in Abb. 20 dargestellt; daher ist es notwendig, die Bewehrung um sie herum zu definieren. Die Verbindung zu allen Knoten der Bewehrung innerhalb des wirksamen Radius wird durch RBE3-Elemente mit gleichem Gewicht sichergestellt.

\[ \textsf{\textit{\footnotesize{Fig. 20\qquad  Patch load mapping to reinforcement mesh.}}}\]

Linienauflager und Linienlasten werden mit RBE3-Elementen, basierend auf der festgelegten Breite oder dem festgelegten wirksamen Radius, mit den Knoten des Betonnetzes verbunden. Das Gewicht der Verbindungen ist anti- proportional zum Abstand vom Auflager- oder Lastimpuls.

3.7     Lösungsmethode und Algorithmus zur Lastkontrolle

Zur Lösung eines nichtlinearen FEM Problems wird ein vollständiger Newton-Raphson (NR) Algorithmus verwendet.The implementation is almost identical to the one presented in.

Generell konvergiert der NR-Algorithmus nicht oft, wenn die volle Last in einem einzigen Schritt angewendet wird. Ein üblicher Ansatz, der auch hier verwendet wird, besteht darin, die Last nacheinander in mehreren Steigerungsstufen anzuwenden und das Ergebnis des vorherigen Laststufe zu verwenden, um die Newton-Lösung einer nachfolgenden Laststufe zu starten. Zu diesem Zweck wurde über dem Newton-Raphson ein Algorithmus zur Laststeuerung implementiert. Für den Fall, dass die NR-Iterationen nicht konvergieren, wird die aktuelle Laststufe auf die Hälfte ihres Werts reduziert und die NR-Iterationen werden wiederholt.

Ein weiterer Zweck des Algorithmus zur Laststeuerung besteht darin, die kritische Last zu ermitteln, die mit bestimmten „Stop-Kriterien“ übereinstimmt - insbesondere der maximalen Dehnung im Beton, dem maximalen Schlupf in den Verbundelementen, der maximalen Verschiebung in den Verankerungselementen und der maximalen Dehnung in den Bewehrungsstäben. Die kritische Last wird mit der Halbierungsmethode ermittelt. Wird das Stop-Kriterium irgendwo im Modell überschritten, werden die Ergebnisse der letzten Laststufe verworfen und eine neue Steife von der halben Größe der vorherigen berechnet. Dieser Vorgang wird wiederholt, bis die kritische Last, mit einer bestimmten Fehlertoleranz, ermittelt ist.

Für Beton wurde das Stop-Kriterium standardmäßig auf eine Druckspannung von 5% (d.h. um eine Größenordnung größer als die tatsächliche Versagensdehnung des Betons) und eine Zugspannung von 7% an den Integrationspunkten der Schalenelemente eingestellt. Unter Zug wurde der Wert so eingestellt, dass zuerst die Grenzdehnung in der Bewehrung erreicht werden kann, die normalerweise bei ca. 5% liegt, ohne die Zugversteifung zu berücksichtigen. Bei Druck wurde der Wert aus mehreren Alternativen ausgewählt, die groß genug sind, damit die Auswirkungen des Quetschens in den Ergebnissen sichtbar werden, aber klein genug, um nicht zu viele Probleme bei der numerischen Stabilität zu verursachen.

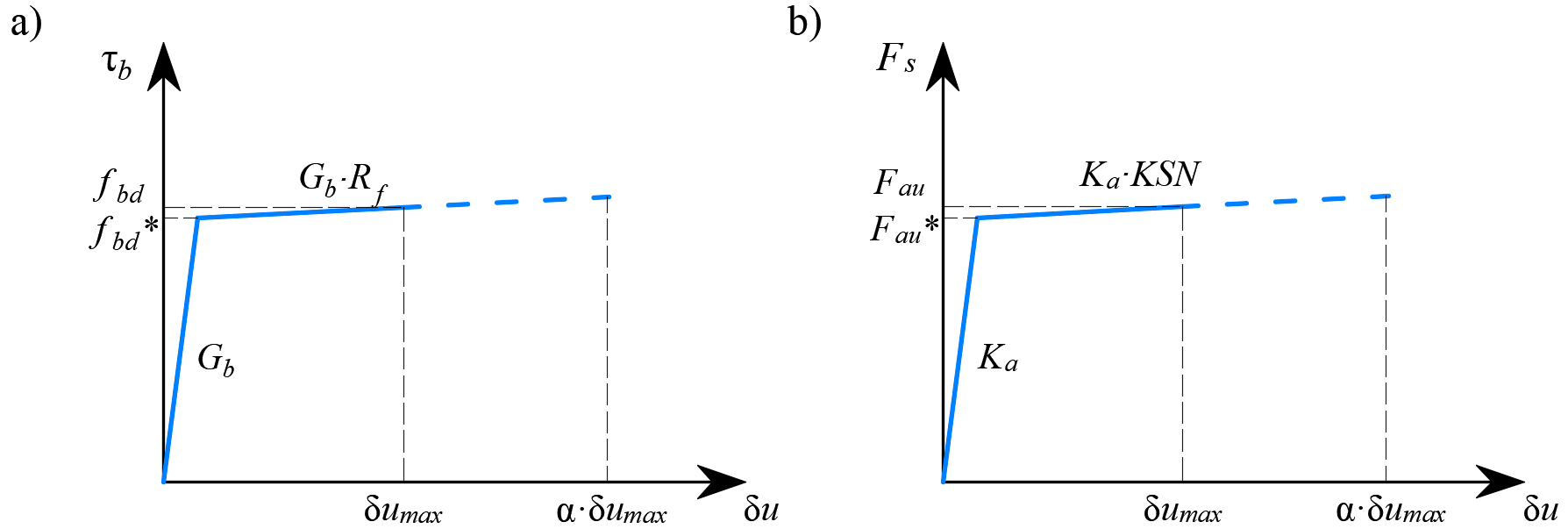
\[ \textsf{\textit{\footnotesize{Fig. 21\qquad Constitutive relationship of bond and anchorage elements used for anchorage length verification:}}}\]

\[ \textsf{\textit{\footnotesize{(a) bond shear stress slip response of a bond element; (b) force-displacement response of an anchorage element.}}}\]

Für Bewehrung wird in Bezug auf Spannungen das Stop-Kriterium definiert. Da die Spannungen am Riss modelliert werden, entspricht das Zugkriterium der Zugfestigkeit der Bewehrung, die den Sicherheitskoeffizienten berücksichtigt.

Das Stop-Kriterium in Verbund- und Verankerungselementen ist α · δ_umax, wobei δ_umax der maximale Schlupf ist, der bei Normnachweisen verwendet wird, und α = 10.

3.8     Darstellung der Ergebnisse

Die Ergebnisse werden unabhängig voneinander für Beton und Bewehrungselemente dargestellt. Die Spannungs- und Dehnungswerte im Beton werden an den Integrationspunkten der Schalenelemente berechnet. Da eine Darstellung der Daten auf diese Weise jedoch nicht praktikabel ist, werden die Ergebnisse standardmäßig in Knoten dargestellt, wie beispielsweise der Maximalwert der Druckspannung von benachbarten Gauß-Integrationspunkten in verbundenen Elementen (Abb. 22). Es ist zu beachten, dass diese Darstellung die Ergebnisse an auf Druck belasteten Bauteilkanten lokal unterschätzen kann, wenn die Größe der finiten Elemente der Tiefe der Druckzone ähnlich ist.

\[ \textsf{\textit{\footnotesize{Fig. 22\qquad  Concrete finite element with integration points and nodes: presentation of the results for concrete in nodes and}}}\]

\[ \textsf{\textit{\footnotesize{in finite elements.}}}\]

Die Ergebnisse für die finiten Elemente der Bewehrung sind entweder für jedes Element konstant (ein Wert - z.B. für Stahlspannungen) oder linear (zwei Werte - für Verbundergebnisse). Für Hilfselemente wie Elemente von Lagerplatten werden nur Verformungen dargestellt.

Lastabtragung an ausgeklinkten Enden von Trägern

In vielen Fällen müssen wir nur ein Detail (einen Teil) eines Bauteils modellieren, wie z.B. eine Balkenauflage, eine Öffnung in der Mitte des Balkens, etc. In solchen Fällen ist es jedoch notwendig, auch den Abschnitt zu modellieren, der den Anschluss an den angrenzenden B-Bereich darstellt, einschließlich der Schnittgrößen in diesem Abschnitt, die das Gleichgewicht erfüllen. In bestimmten Fällen (z.B. bei der Modellierung von Balkenauflagern) können diese Schnittgrößen vom Programm automatisch ermittelt werden.

Zwischen der B-Region und dem untersuchten Diskontinuitätsbereich wird automatisch eine Saint-Venant-Transferzone erzeugt, um eine realistische Spannungsverteilung in dem untersuchten Bereich zu gewährleisten. Die Breite der Transferzone wird auf die Hälfte der Tiefe des Querschnitts festgelegt. Da der einzige Zweck der Saint-Venant-Zone darin besteht, eine korrekte Spannungsverteilung im Rest des Modells zu erreichen, werden bei der Überprüfung keine Ergebnisse aus diesem Bereich angezeigt, und es werden hier keine Abbruchkriterien berücksichtigt.

Die Kante der Saint-Venant-Zone, die das ausgeklinkte Ende des Trägers darstellt, wird als starr modelliert, d. h. sie kann sich drehen, muss aber in der Ebene ruhen. Dazu werden alle FEM-Knoten der Kante mit einem separaten Knoten im Trägheitszentrum des Querschnitts über ein Starrkörperelement (RBE2) verbunden. An diesem Knoten können dann die Schnittgrößen des Elements angesetzt werden, wie in Abb. 12 dargestellt.

\[ \textsf{\textit{\footnotesize{Abb. 12\qquad Übertragung von Schnittgrößen an einem ausgeklinkten Ende.}}}\]

Geometrische Änderung von Querschnitten

Bei Geometrien mit Vouten wird die Breite der Wandelemente, die zur Modellierung der Voute verwendet werden, im Vergleich zur ursprünglichen Breite reduziert, so dass sie der doppelten Höhe plus der Dicke der angrenzenden Wand entspricht. Dies beruht auf der Annahme, dass sich ein Druckspannungsfeld in einem 45°-Winkel von der Wand aus ausdehnt (siehe Abb. 13), so dass die vorgenannte reduzierte Breite die maximale Breite ist, die Lasten übertragen kann.

Beachten Sie, dass die in CSFM implementierte Methode zur Bestimmung der effektiven Flanschbreite sich von der in 5.3.2.1 DIN EN 1992-1-1 (2015) angegebenen Methode unterscheidet. Neben der Geometrie wird die nach Eurocode ermittelte effektive Flanschbreite explizit von den Spannweiten und den Randbedingungen eines Bauwerks beeinflusst.

\[ \textsf{\textit{\footnotesize{Abb. 13\qquad Breitenreduzierung eines Querschnitts: (a) Benutzereingabe; (b) FE-Modell - automatisch ermittelte reduzierte Flanschbreite}}}\]

Bei Vouten, die in der horizontalen Ebene liegen (Abb. 14), wird jede Voute in fünf Abschnitte entlang ihrer Länge unterteilt. Jeder dieser Abschnitte wird dann als Wand mit einer konstanten Dicke modelliert, die der tatsächlichen Dicke in der Mitte des jeweiligen Abschnitts entspricht.

\[ \textsf{\textit{\footnotesize{Abb. 14\qquad Horizontale Voute: (a) Benutzereingabe; (b) FE-Modell - eine automatisch in fünf Abschnitte unterteilte Voute}}}\]

Bemessungsgrundlagen: Finite-Elemente-Typen

Das nichtlineare Finite-Elemente-Analysemodell besteht aus mehreren Arten von Finite-Elementen, die zur Modellierung des Betons, der Bewehrung und des Verbunds zwischen diesen Elementen verwendet werden. Die Beton- und Betonstahlelemente werden zunächst unabhängig voneinander vernetzt und dann mit Hilfe von Multi-Point-Constraints (MPC-Elementen) miteinander verbunden. Dadurch kann die Bewehrung eine beliebige, relative Position zum Beton einnehmen. Soll der Nachweis der Verankerungslänge berechnet werden, werden zwischen der Bewehrung und den MPC-Elementen Verbund- und Verankerungsendfederelemente eingefügt.

\[ \textsf{\textit{\footnotesize{Fig. 13\qquad Finite-Elemente-Modell: Bewehrungselemente, die unter Verwendung von MPC-Elementen und Verbundelementen auf ein Betonnetz abgebildet werden.}}}\]

Beton

Beton wird mit vier- und dreiseitigen Schalenelementen, CQUAD4 und CTRIA3, modelliert. Bei diesen Elementen wird nur von ebenen Spannungen ausgegangen, d. h. Spannungen oder Dehnungen in z-Richtung werden nicht berücksichtigt.

Jedes Element hat vier bzw. drei Integrationspunkte, die bei etwa 1/4 seiner Größe platziert sind. An jedem Integrationspunkt in jedem Element werden die Richtungen der Hauptdehnungen α₁, α₂berechnet. In diesen beiden Richtungen werden die Hauptspannungen σ_c1, σ_c2 und die Steifigkeiten E₁, E₂ nach dem vorgegebenen Betonspannungs-Dehnungs-Diagramm gemäß Abb. 2 bewertet. Es ist zu beachten, dass der Einfluss der Druckentlastung wegen der Betonrissbildung berücksichtigt wird.

Bewehrung

Bewehrungsstäbe werden durch 1D-Stab"-Elemente (CROD) mit zwei Knoten modelliert, die nur eine axiale Steifigkeit aufweisen. Diese Elemente sind mit speziellen "Bond"-Elementen verbunden, die entwickelt wurden, um das Verbundverhalten zwischen einem Bewehrungsstab und dem umgebenden Beton zu modellieren. Diese Verbundelemente werden anschließend über MPC-Elemente (Multi-Point-Constraint) mit dem Netz verbunden, das den Beton darstellt. Dieser Ansatz ermöglicht die unabhängige Vernetzung von Bewehrung und Beton, während ihre Verbindung untereinander später sichergestellt wird.

Verbundelemente

Der Nachweis der Verankerungslänge erfolgt durch die Implementierung der Verbundschubspannungen zwischen Betonelementen (2D) und Bewehrungselementen (1D) in das Finite-Elemente-Modell. Zu diesem Zweck wurde ein Finite-Elemente-Typ "Verbund" entwickelt.

Die Definition des Verbundelements ist ähnlich der eines Schalenelements (CQUAD4). Es ist ebenfalls durch 4 Knoten definiert, hat aber im Gegensatz zur Schale nur zwischen den beiden oberen und den beiden unteren Knoten eine Schersteifigkeit ungleich Null. Im Modell sind die oberen Knoten mit den Elementen verbunden, die die Bewehrung darstellen, und die unteren Knoten mit denen, die den Beton darstellen. Das Verhalten dieses Elements wird durch die Verbundspannung τ_b, als bilineare Funktion des Schlupfes zwischen dem oberen und dem unteren Knoten δ_u, beschrieben, siehe Abb. 14.

\[ \textsf{\textit{\footnotesize{Fig. 14\qquad (a) konzeptionelle Darstellung der Verformung eines Verbundelements; (b) eine Spannungs-Verformungs-Funktion.}}}\]

Der elastische Steifigkeitsmodul der Bond-Slip-Beziehung, G_b, ist wie folgt definiert:

\[G_b = k_g \cdot \frac{E_c}{Ø}\]

mit:

k_g            Koeffizient in Abhängigkeit von der Oberfläche des Bewehrungsstabs (standardmäßig kg = 0,2)

E_c            Elastizitätsmodul des Betons (im Fall von EN als E_cm angenommen)

Ø             Durchmesser des Bewehrungsstabs

Für den Nachweis der Verankerungslänge werden die Bemessungswerte (faktorisierte Werte) der Verbundschubspannung f_bd verwendet, die in den jeweils gewählten Bemessungsnormen angegeben sind. Die Verfestigung des plastischen Astes wird standardmäßig mit G_b/10⁵ berechnet.

Verankerungsfeder

Das Anbringen von Verankerungen an den Bewehrungsstäben (z. B. Haken, Schlaufen...), die den Vorschriften der Bemessungsregeln entsprechen, ermöglicht die Verringerung der Grundverankerungslänge der Stäbe (l_b,net) um einen bestimmten Faktor β (im Folgenden als "Verankerungskoeffizient" bezeichnet). Der Bemessungswert der Verankerungslänge (l_b) wird dann wie folgt berechnet:

\[l_b = \left(1 - \beta\right)l_{b,net}\]

Die vorgesehene Reduzierung in l_b,net entspricht der Aktivierung des Bewehrungsstabes an seinem Ende mit einem Prozentsatz seiner maximalen Kapazität, die durch den Verankerungsabnahmekoeffizienten gegeben ist, wie in Abb. 15a gezeigt.

\[ \textsf{\textit{\footnotesize{Fig. 15\qquad  Modell für die Reduzierung der Verankerungslänge:}}}\]

\[ \textsf{\textit{\footnotesize{(a) Verankerungskraft entlang der Verankerungslänge des Bewehrungsstabs; (b) Zusammenhang zwischen Schlupf und Verankerungskraft.}}}\]

Die Verringerung der Verankerungslänge wird im Finite-Elemente-Modell durch ein Federelement am Stabende berücksichtigt (Abb. 15), das durch das in Abb. 15b dargestellte konstitutive Modell definiert ist. Die maximale Kraft, die von dieser Feder übertragen wird (F_au), beträgt:

\[F_{au} = \beta \cdot A_s \cdot f_{yd}\]

mit :

β             der Verankerungskoeffizient auf der Grundlage der Verankerungsart,

A_s            der Querschnitt des Bewehrungsstabs,

f_yd           der Bemessungswert (faktorisierter Wert) der Streckgrenze der Bewehrung.

Vernetzung

Die finiten Elemente werden intern implementiert und das Analysemodell wird automatisch generiert, ohne dass eine kompetente Benutzerinteraktion erforderlich ist. Ein wichtiger Teil dieses Prozesses ist die Vernetzung.

Beton

Alle Betonbauteile sind miteinander vernetzt. Eine empfohlene Elementgröße wird automatisch von der Anwendung basierend auf der Größe und Form der Struktur und unter Berücksichtigung des Durchmessers des größten Bewehrungsstabs berechnet. Darüber hinaus garantiert die empfohlene Elementgröße, dass in dünnen Teilen der Struktur, wie z.B. schlanken Stützen oder dünnen Decken, mindestens 4 Elemente generiert werden, um in diesen Bereichen zuverlässige Ergebnisse zu gewährleisten. Die maximale Anzahl von Betonelementen ist auf 5000 begrenzt, aber dieser Wert reicht aus, um die empfohlene Elementgröße für die meisten Bauwerke bereitzustellen. Konstrukteure können jederzeit eine benutzerdefinierte Betonelementgröße auswählen, indem sie den Multiplikator der Standardnetzgröße ändern.

Bewehrung

Die Bewehrung wird in Elemente unterteilt, deren Länge ungefähr der Betonelementgröße entspricht. Sobald die Bewehrungs- und Betonmatten erstellt sind, werden sie mit Verbundelementen (GZT) oder direkt durch MPC-Elemente (GZG) miteinander verbunden, wie in Abb. 15 gezeigt.

Lagerplatten

Hilfskonstruktionsteile wie Lagerplatten werden unabhängig voneinander vernetzt. Die Größe dieser Elemente wird mit 2/3 der Größe der Betonelemente im Verbindungsbereich berechnet. Die Knoten des Netzes der Lagerplatte werden dann mit den Randknoten des Betonnetzes unter Verwendung von Interpolationsbeschränkungselementen (RBE3) verbunden.

Lasten und Lagerungen

Teillasten und Teilauflager sind nur mit der Bewehrung verbunden, wie in Abb. 20 gezeigt. Daher ist es notwendig, die Bewehrung um sie herum zu definieren. Der Anschluss an alle Knoten der Bewehrung innerhalb des wirksamen Radius wird durch RBE3-Elemente mit gleichem Gewicht sichergestellt.

\[ \textsf{\textit{\footnotesize{Abb. 20\qquad  Zuordnen der Teillast zu Bewehrungsnetzen.}}}\]

Linienlager und Linienlasten werden mit RBE3-Elementen auf Basis der vorgegebenen Breite bzw. des wirksamen Radius an die Knoten des Betonnetzes angeschlossen. Das Gewicht der Verbindungen ist umgekehrt proportional zum Abstand vom Lager- oder Lastimpuls.

Lösungsverfahren und Algorithmus zur Laststeuerung

Ein standardmäßiger vollständiger Newton-Raphson-Algorithmus (NR) wird verwendet, um die Lösung eines nichtlinearen FEM-Problems zu finden.

Im Allgemeinen konvergiert der NR-Algorithmus oft nicht, wenn die volle Last in einem einzigen Schritt aufgebracht wird. Ein üblicher Ansatz, der auch hier verwendet wird, besteht darin, die Last sequentiell in mehreren Inkrementen aufzubringen und das Ergebnis des vorherigen Lastinkrements zu verwenden, um die Newton-Lösung eines nachfolgenden Inkrements zu starten. Zu diesem Zweck wurde ein Lastkontrollalgorithmus zusätzlich zum Newton-Raphson implementiert. Für den Fall, dass die NR-Iterationen nicht konvergieren, wird das aktuelle Lastinkrement auf die Hälfte seines Wertes reduziert und die NR-Iterationen werden erneut versucht.

Ein zweiter Zweck des Lastkontrollalgorithmus besteht darin, die kritische Last zu finden, die bestimmten "Stoppkriterien" entspricht - insbesondere der maximalen Dehnung im Beton, dem maximalen Schlupf in den Verbundelementen, der maximalen Verschiebung in den Verankerungselementen und der maximalen Dehnung in den Bewehrungsstäben. Die kritische Last wird mit Hilfe der Halbierungsmethode ermittelt. Wird das Stoppkriterium irgendwo im Modell überschritten, werden die Ergebnisse des letzten Lastinkrements verworfen und ein neues Inkrement mit der Hälfte der Größe des vorherigen berechnet. Dieser Vorgang wird so lange wiederholt, bis die kritische Last mit einer bestimmten Fehlertoleranz gefunden ist.

Für Beton wurde das Abbruchkriterium standardmäßig auf eine Druckdehnung von 5 % (d. h. etwa eine Größenordnung größer als die tatsächliche Versagensdehnung von Beton) und eine Zugdehnung von 7 % an den Integrationspunkten der Schalenelemente festgelegt. Im Zug wurde der Wert so gewählt, dass die Grenzdehnung in der Bewehrung, die ohne Berücksichtigung der Zugversteifung in der Regel bei 5 % liegt, zuerst erreicht wird. Im Druckbereich wurde der Wert aus mehreren Alternativen so gewählt, dass er groß genug ist, um die Auswirkungen der Quetschung in den Ergebnissen sichtbar werden zu lassen, aber klein genug, um nicht zu viele Probleme mit der numerischen Stabilität zu verursachen.

\[ \textsf{\textit{\footnotesize{Abb. 21\qquad Konstitutive Beziehung von Verbund- und Verankerungselementen, die für den Nachweis der Verankerungslänge verwendet werden:}}}\]

\[ \textsf{\textit{\footnotesize{((a) Scherspannungs-Schlupfverhalten eines Verbundelements; (b) Kraft-Weg-Verhalten eines Verankerungselements}}}\]

Für die Bewehrung wird das Anhaltekriterium in Form von Spannungen definiert. Da die Spannungen am Riss modelliert werden, entspricht das Kriterium auf Zug der Zugfestigkeit der Bewehrung unter Berücksichtigung des Sicherheitsbeiwerts. Derselbe Wert wird für das Kriterium in Druckrichtung verwendet.

Das Anhaltekriterium in Verbund- und Verankerungselementen ist α·δu_max, wobei δu_maxder maximale Schlupf ist, der in den Code-Nachweisen verwendet wird, und α = 10.

Präsentation der Ergebnisse

Die Ergebnisse werden unabhängig voneinander für Beton und für Bewehrungselemente dargestellt. Die Spannungs- und Dehnungswerte im Beton werden an den Integrationspunkten der Schalenelemente berechnet. Da es jedoch nicht praktikabel ist, die Daten auf diese Weise darzustellen, werden die Ergebnisse standardmäßig in Knoten dargestellt, wie der Maximalwert der Druckspannung von benachbarten Gauß-Integrationspunkten in verbundenen Elementen (Abb. 22). 

\[ \textsf{\textit{\footnotesize{Abb. 22\qquad  Finites Element aus Beton mit Integrationspunkten und -knoten: Darstellung der Ergebnisse für Beton in Knoten und}}}\]

\[ \textsf{\textit{\footnotesize{in finiten Elementen.}}}\]

Die Ergebnisse für die finiten Elemente der Bewehrung sind entweder für jedes Element konstant (ein Wert - z. B. für Stahlspannungen) oder linear (zwei Werte - für Verbundergebnisse). 

4 Verifizierung der Strukturelemente

Die Bewertung der Struktur mittels CSFM erfolgt durch zwei verschiedene Analysen: Eine für Kombinationen der Gebrauchstauglichkeit, und eine für Kombinationen des Grenzzustandes der Tragfähigkeit. Die Analyse der Gebrauchstauglichkeit geht davon aus, dass das Grenzverhalten des Elements ausreichend ist und die Fließbedingungen des Materials auf dem Level der Gebrauchstauglichkeit nicht erreicht werden. Dieser Ansatz ermöglicht die Verwendung vereinfachter Werkstoffmodelle (mit einem linearen Zweig des Spannungs-Dehnungs-Diagramms des Betons) für die Analyse der Gebrauchstauglichkeit, um die numerische Stabilität und die Berechnungsgeschwindigkeit zu verbessern. Daher wird die Verwendung des unten dargestellten Workflows empfohlen, bei dem als erster Schritt die Analyse des Grenzzustands der Tragfähigkeit durchgeführt wird.

4.1     GZT Analyse

Die Bewertung der verschiedenen Überprüfungen, die für bestimmte Bemessungsnormen erforderlich sind, erfolgt auf der Grundlage der direkten Ergebnisse des Modells. GZT-Nachweise werden für die Betonfestigkeit, Bewehrungsfestigkeit und Verankerung (Verbundschubspannungen) durchgeführt.

Um sicherzustellen, dass ein Strukturelement effizient konstruiert ist, wird dringend empfohlen, eine vorläufige Analyse durchzuführen, die die folgenden Schritte berücksichtigt:

• Auswahl der am meisten kritischen Lastkombinationen treffen
• Nur Lastkombinationen für den Grenzzustand der Tragfähigkeit (GZT) berechnen
• Ein grobes Netz verwenden (Erhöhen des Multiplikators der Standardnetzgröße, Abb.23

\[ \textsf{\textit{\footnotesize{Fig. 23\qquad Mesh multiplier.}}}\]

Ein solches Modell lässt sich sehr schnell berechnen, sodass Konstrukteure die Detaillierung des Strukturelements effizient überprüfen und die Analyse erneut ausführen können, bis alle Anforderungen an die Überprüfung für die kritischsten Lastkombinationen erfüllt sind. Sind alle Anforderungen an die Überprüfung dieser vorläufigen Analyse erfüllt, wird empfohlen, die vollständigen Grenzlastkombinationen und die Verwendung einer feinen Netzgröße (vom Programm empfohlene Netzgröße) einzubeziehen. Der Anwender kann die Netzgröße durch den Multiplikator (Wert von 0,5 bis 5) ändern.

Die Basisergebnisse und Überprüfungen (Spannung, Dehnung und Ausnutzung (d.h. der aus der Norm berechnete Wert/Grenzwert) sowie die Richtung der Hauptspannungen bei Betonelementen) werden anhand verschiedener Diagramme angezeigt, in denen die Druckbereiche in der Regel in rot und Zugbereiche in blau dargestellt werden.

Es können globale Minimal- und Maximalwerte für die gesamte Struktur sowie Minimal- und Maximalwerte für jedes benutzerdefinierte Teil hervorgehoben werden. In einem separaten Tab können erweiterte Ergebnisse wie Tensorwerte, Verformungen der Struktur und Bewehrungsanteile (effektiv und geometrisch) angezeigt werden, die zur Berechnung der Zugversteifung der Bewehrungsstäbe verwendet werden. Darüber hinaus können Lasten und Lagerreaktionen für ausgewählte Kombinationen oder Lastfälle dargestellt werden.

4.2     GZG Analyse

GZG Auswertungen erfolgen für Spannungsbegrenzung, Rissbreite und Durchbiegungsgrenzen.

Die Spannungen in Beton- und Bewehrungselementen werden gemäß der geltenden Norm auf ähnliche Weise wie für die im GZT festgelegten nachgewiesen.

Die Analyse der Gebrauchstauglichkeit enthält bestimmte Vereinfachungen der Werkstoffmodelle, die für die finale Analyse des GZT verwendet werden. Es wird ein perfekter Verbund wird angenommen, d.h. die Verankerungslänge wird bei Gebrauchstauglichkeit nicht überprüft. Weiterhin wird der plastische Zweig der Spannungs-Dehnungs-Kurve von Beton bei Druck nicht berücksichtigt, während der elastische Zweig linear und unendlich ist. Diese Vereinfachungen verbessern die numerische Stabilität und die Berechnungsgeschwindigkeit, verringern aber gleichzeitig nicht die Allgemeinheit der Lösung, solange die resultierenden Grenzwerte für die Materialspannung bei Erreichen der Gebrauchstauglichkeit deutlich unter ihren Streckgrenzen liegen (wie von Normen gefordert). Daher sind die für die Gebrauchstauglichkeit verwendeten vereinfachten Modelle nur gültig, wenn alle Anforderungen zur Überprüfung erfüllt sind.

4.2.1  Berechnung der Rissbreite

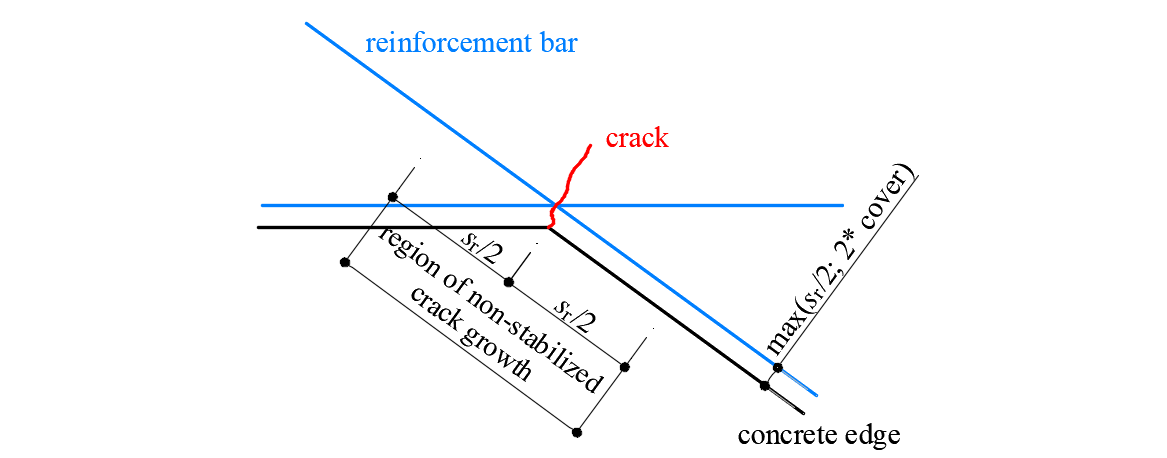
Es gibt zwei Möglichkeiten zur Berechnung von Rissbreiten: stabilisierte und nicht stabilisierte Risse. Entsprechend dem geometrischen Bewehrungsanteil in jedem Teil der Struktur wird entschieden, welche Art von Rissberechnungsmodell verwendet wird (TCM für stabilisierte Rissmodelle und POM für nicht stabilisierte Rissmodelle).

\( \textsf{\textit{\footnotesize{Fig. 24 \qquad Crack width calculation: (a) considered crack kinematics; (b) projection of crack kinematics into the principal}}}\) \( \textsf{\textit{\footnotesize{directions of the reinforcing bar; (c) crack width in the direction of the reinforcing bar for stabilized cracking; (d) cases with}}}\) \( \textsf{\textit{\footnotesize{local non-stabilized cracking regardless of the reinforcement amount; (e) crack width in the direction of the reinforcing bar}}}\)\( \textsf{\textit{\footnotesize{for non-stabilized cracking.}}}\)

Während die CSFM für die meisten Überprüfungen (z.B. Bauteilkapazität, Durchbiegungen ...) ein direktes Ergebnis liefert, werden die Ergebnisse der Rissbreite aus den Ergebnissen der Bewehrungsdehnung berechnet, die direkt durch die FE-Analyse, gemäß der in Abb. 24 beschriebenen Methodik, bereitgestellt werden. Es wird eine Risskinematik ohne Schlupf (reine Rissöffnung) betrachtet (Abb. 24a), die mit den Hauptannahmen des Modells übereinstimmt. Die Hauptrichtungen der Spannungen und Dehnungen definieren die Neigung der Risse (θ_r = θ_s = θ_e). Gemäß Abb. 24b kann die Rissbreite (w) in Richtung des Bewehrungsstabs (w_b) projiziert werden, was zu folgender Definition führt:

\[w = \frac{w_b}{\cos\left(θ_r + θ_b - \frac{π}{2}\right)}\]

mit θ_b als Stabneigung.

Die Berechnung der Komponente w_b erfolgt konsistent, basierend auf den in Abschnitt 1.2.4 vorgestellten Zugversteifungsmodellen, durch Integration der Bewehrungsdehnungen. Für diese Bereiche mit voll entwickelten Rissmustern werden, wie in Abb. 24c angegeben, die berechneten durchschnittlichen Dehnungen (e_m) entlang der Bewehrungsstäbe direkt entlang des Rissabstands (s_r) integriert. Während dieser Ansatz zur Berechnung der Rissrichtungen nicht der tatsächlichen Position der Risse entspricht, liefert er dennoch repräsentative Werte, die zu Ergebnissen der Rissbreite führen, die mit den von der Norm geforderten Werten an der Position des Bewehrungsstabs verglichen werden können.

Besondere Situationen werden an konkaven Ecken der berechneten Struktur beobachtet. In diesem Fall definiert die Ecke die Position eines einzelnen Risses, der sich nicht stabilisiert verhält, bevor sich zusätzliche benachbarte Risse entwickeln. Diese zusätzlichen Risse entstehen in der Regel nach dem Bereich der Gebrauchstauglichkeit (Mata-Falcón 2015), der die Berechnung der Rissbreiten in einem solchen Bereich rechtfertigt, als wären sie nicht stabilisiert (Abb. 25), unter Verwendung des in Abschnitt 1.2.4 dargestellten Modells.

\[ \textsf{\textit{\footnotesize{Fig. 25\qquad Definition of the region at concave corners in which the crack width is computed as if it were non-stabilized.}}}\]

Bemessung nach Eurocode

Die Bemessung mit Hilfe des CSFM erfolgt durch zwei verschiedene Analysen: eine für die Gebrauchstauglichkeit und eine für die LF-Kombination im Grenzzustand der Tragfähigkeit. Bei der Gebrauchstauglichkeitsanalyse wird davon ausgegangen, dass das Tragverhalten des Elements zufriedenstellend ist und die Fließbedingungen des Materials bei den Gebrauchstauglichkeitslaststufen nicht erreicht werden. Dieser Ansatz ermöglicht die Verwendung vereinfachter konstitutiver Modelle (mit einem linearen Zweig des Betonspannungs-Dehnungs-Diagramms) für die Gebrauchstauglichkeitsanalyse, um die numerische Stabilität und die Berechnungsgeschwindigkeit zu erhöhen.

Materialien

Beton - GZT

Das in der CSFM implementierte Betonmodell basiert auf den Werkstoffgesetzen für einachsigen Druck, die in DIN EN 1992-1-1 für die Bemessung von Querschnitten, die nur von der Druckfestigkeit abhängen, vorgeschrieben sind. Das in DIN EN 1992-1-1 (Abb. 26a) angegebene Parabel-Rechteck-Diagramm wird in der CSFM standardmäßig verwendet; Konstrukteure können jedoch auch ein vereinfachtes, elastisch ideal plastisches Verhältnis wählen (Abb. 26b). Wie es bei der Bemessung von klassischem Stahlbeton der Fall ist, wird die Zugfestigkeit vernachlässigt.

\[ \textsf{\textit{\footnotesize{Fig. 26\qquad The stress-strain diagrams of concrete for ULS: a) parabola-rectangle diagram; b) bilinear diagram.}}}\]

Unter Verwendung der Standardeinstellungen berücksichtigt die aktuelle Implementierung der CSFM in IDEA StatiCa Detail kein explizites Versagenskriterium in Bezug auf Dehnungen für Druckbeton (d.h. nach Erreichen der Spannungsspitze wird ein plastischer Zweig mit ε_cu2 (ε_cu3) mit einem Wert von 5% berücksichtigt, während DIN EN 1992-1-1 eine Grenzdehnung von weniger als 0,35% annimmt). Diese Vereinfachung macht die Überprüfung der Verformungskapazität von Strukturen, die bei Druck versagen, nicht möglich. Ihre finale Kapazität wird jedoch korrekt vorhergesagt, wenn zusätzlich zu dem in Abb. 2e definierten Faktor für gerissenen Beton (k_c2, siehe Abb. 27)) die Zunahme der Sprödigkeit von Beton mit zunehmender Festigkeit anhand des in der fib Modellnorm 2010 definierten Reduktionsfaktors wie folgt berücksichtigt wird:

\[f_{cd}=\frac{f_{ck,red}}{γ_c} = \frac{k_c \cdot f_{ck}}{γ_c} = \frac{\eta _{fc} \cdot k_{c2} \cdot f_{ck}}{γ_c}\]

\[{\eta _{fc}} = {\left( {\frac{{30}}{{{f_{ck}}}}} \right)^{\frac{1}{3}}} \le 1\]

wo:

k_c  – Globaler Reduktionsfaktor der Druckfestigkeit

k_c2 – Reduktionsfaktor aufgrund von Querrissen

f_ck – Charakteristische Festigkeit des Betonzylinders (in MPa zur Definition von η_fc.

\[ \textsf{\textit{\footnotesize{Fig. 27\qquad The compression softening law.}}}\]

Beton - GZG

Die Analyse zur Gebrauchstauglichkeit enthält bestimmte Vereinfachungen der Werkstoffmodelle, die für die GZT Analyse verwendet werden. Es wird ein perfekter Verbund angenommen, d.h. die Verankerungslänge wird bei der Gebrauchstauglichkeit nicht überprüft.

Weiterhin wird der plastische Zweig der Spannungs-Dehnungs-Kurve von auf Druck belastetem Beton nicht berücksichtigt, während der elastische Zweig linear und unendlich ist. Das Gesetz zur Druckentfestigung wird nicht berücksichtigt. Diese Vereinfachungen verbessern die numerische Stabilität und Berechnungsgeschwindigkeit, verringern jedoch nicht die Allgemeinheit der Lösung, solange die resultierenden Grenzwerte für die Materialspannung bei Gebrauchstauglichkeit deutlich unter ihren Streckgrenzen liegen (wie vom Eurocode gefordert). Daher sind die für die Gebrauchstauglichkeit verwendeten, vereinfachten Modelle nur gültig, wenn alle Anforderungen zur Überprüfung erfüllt sind.

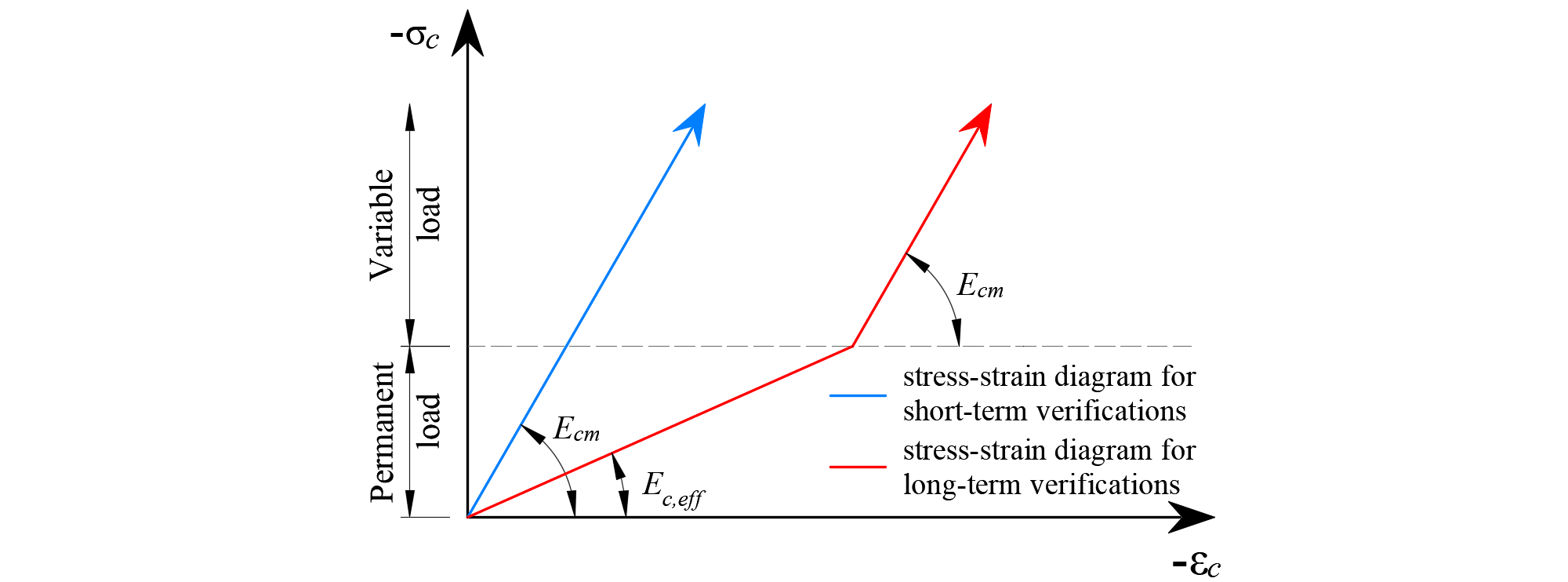
\[ \textsf{\textit{\footnotesize{Fig. 28\qquad Concrete stress-strain diagrams implemented for serviceability analysis: short- and long-term verifications.}}}\]

Langfristige Auswirkungen

Bei der Analyse der Gebrauchstauglichkeit werden die langfristigen Auswirkungen von Beton unter Verwendung eines wirksamen unendlichen Kriechkoeffizienten (φ, standardmäßig mit 2,5 angenommen) betrachtet, der den Sekantenmodul der Elastizität des Betons (E_cm) wie folgt bearbeitet:

\[E_{c,eff} = \frac{E_{cm}}{1+\varphi}\]

Bei der Betrachtung von langfristigen Auswirkungen wird zunächst ein Lastschritt mit allen ständigen Lasten, unter Berücksichtigung des Kriechkoeffizienten (d.h .unter Verwendung des wirksamen E-Mduls von Beton, E_c,eff) berechnet, und anschließend werden die zusätzlichen Lasten ohne den Kriechkoeffizienten berechnet (d.h. unter Verwendung von E_cm). Um kurzfristige Überprüfungen durchzuführen, wird zusätzlich eine weitere Berechnung durchgeführt, bei der alle Lasten ohne den Kriechkoeffizienten berechnet werden. Beide Berechnungen für Langzeit- und Kurzzeitüberprüfungen sind in Abb. 28 dargestellt.

Bewehrung

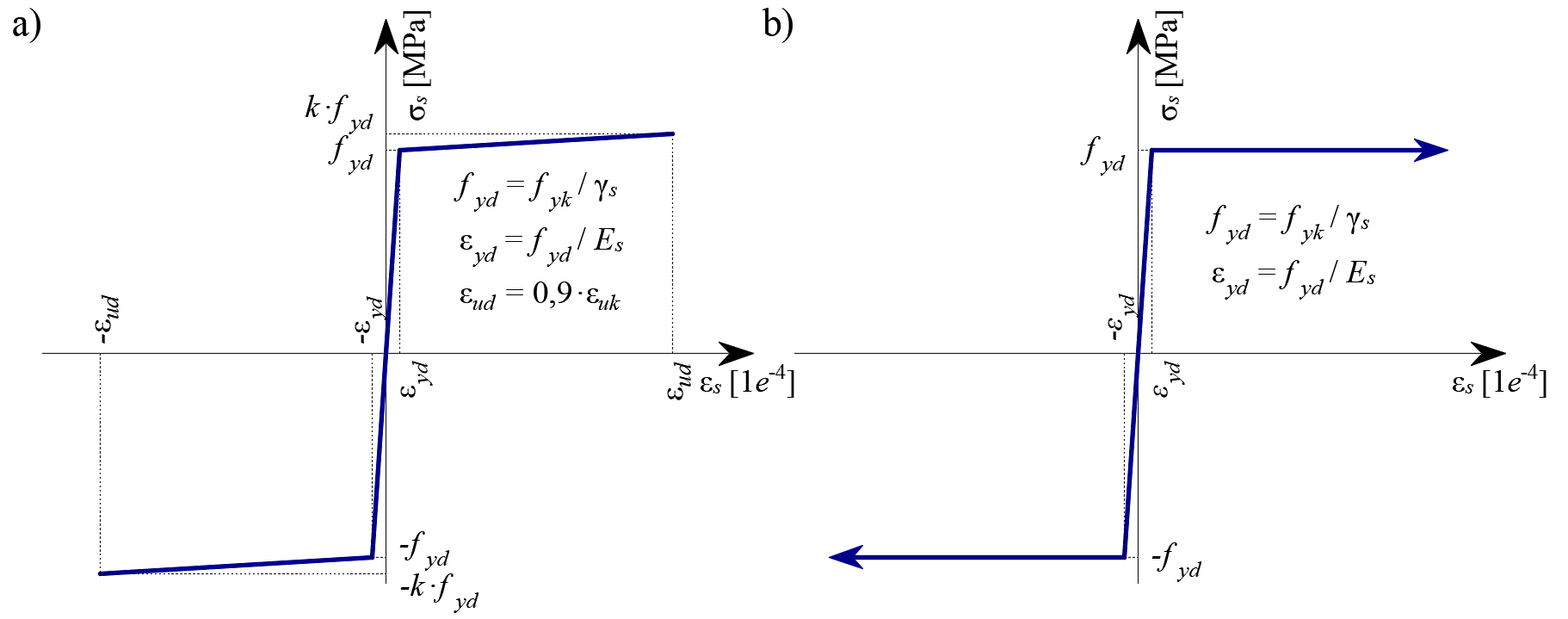
Standardmäßig wird das idealisierte bilineare Spannungs-Dehnungs-Diagramm für die blanken Bewehrungsstäbe berücksichtigt, die typischerweise durch Bemessungsnormen (Abb. 29) definiert sind. Die Definition dieses Diagramms erfordert nur, dass die grundlegenden Eigenschaften der Bewehrung während der Bemessungsphase bekannt sind (Festigkeits- und Duktilitätsklasse). Wann immer bekannt, kann das reale Spannungs-Dehnungs-Verhältnis der Bewehrung (warmgewalzt, kaltverformt, abgeschreckt und selbsttemperiert, etc.) berücksichtigt werden. Das Spannungs-Dehnungs-Diagramm der Bewehrung kann vom Benutzer definiert werden. In diesem Fall ist es jedoch unmöglich, den Effekt der Zugversteifung anzunehmen (eine Berechnung der Rissbreite ist nicht möglich). Die Verwendung des Spannungs-Dehnungs-Diagramms mit horizontalem oberem Ast ermöglicht keine Überprüfung der strukturellen Haltbarkeit. Daher ist eine manuelle Überprüfung der Standardanforderungen an die Duktilität erforderlich.

\( \textsf{\textit{\footnotesize{Fig. 29 \qquad Stress-strain diagram of reinforcement: a) bilinear diagram with an inclined top branch; b) bilinear diagram}}}\) \( \textsf{\textit{\footnotesize{with a horizontal top branch.}}}\)

Zugversteifung (Abb. 30) wird automatisch berücksichtigt, indem das Verhältnis von Eingangsspannung zu Dehnung des blanken Bewehrungsstabs bearbeitet wird, um die durchschnittliche Steifigkeit der im Beton eingebetteten Stäbe (ε_m) gemäß den in Abschnitt 1.2.4 dargestellten Ansätzen zu erfassen.

\[ \textsf{\textit{\footnotesize{Fig. 30\qquad Scheme of tension stiffening.}}}\]

Teilsicherheitsbeiwerte

Teilsicherheitsbeiwerte

Die kompatible Spannungsfeldmethode entspricht den heutigen Bemessungsnormen (Eurocode 2). Da die Berechnungsmodelle nur Eigenschaften von Standardmaterialien verwenden, kann das in den Bemessungsnormen vorgeschriebene Format des Teilsicherheitsfaktors ohne Anpassung angewendet werden. Auf diese Weise werden die eingegebenen Lasten berücksichtigt und die charakteristischen Materialeigenschaften unter Verwendung der jeweiligen Sicherheitsfaktoren reduziert, die in den Bemessungsnormen, genau wie bei der herkömmlichen Betonanalyse, vorgeschrieben sind. Werte der Sicherheitsfaktoren in EN 1992-1-1 Kap. 2.4.2.4 sind standardmäßig eingestellt, der Anwender kann sie jedoch in den Einstellungen ändern (Abb. 31).

\[ \textsf{\textit{\footnotesize{Fig. 31\qquad Die Einstellung der materiellen Sicherheitsfaktoren in Idea StatiCa Detail.}}}\]

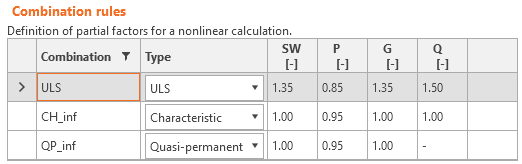
Lastsicherheitsfaktoren müssen vom Anwender in der Kombinationsregel für jede nichtlineare Lastfallkombination definiert werden (Abb. 32). Für alle in IDEA StatiCa Detail implementierten Vorlagen sind die Teilsicherheitsfaktoren bereits vordefiniert.

\[ \textsf{\textit{\footnotesize{Fig. 32\qquad Die Einstellung der Lastteilfaktoren in Idea StatiCa Detail.}}}\]

Grenzzustand der Tragfähigkeit

Die verschiedenen von DIN EN 1992-1-1 geforderten Nachweise werden auf der Grundlage der direkten Ergebnisse des Modells bewertet. Die GZT-Nachweise werden für die Betonfestigkeit, die Bewehrungsfestigkeit und die Verankerung (Verbundschubspannungen) geführt.

Die Druckfestigkeit des Betons wird als das Verhältnis zwischen der maximalen Hauptdruckspannung σc_{= σc2} aus der FE-Analyse und dem Grenzwert σc_,lim = _fcd bewertet.

Die Festigkeit der Bewehrung wird sowohl auf Zug als auch auf Druck als das Verhältnis zwischen der Spannung in der Bewehrung an den Rissen _σsr und dem festgelegten Grenzwert σs_,lim bewertet:

\(σ_{s,lim} = \frac{k \cdot f_{yk}}{γ_s}\qquad\qquad\textsf{\small{für bilineares Diagramm mit geneigtem oberen Ast}}\)

\(σ_{s,lim} = \frac{f_{yk}}{γ_s}\qquad\qquad\,\,\,\,\textsf{\small{für bilineares Diagramm mit horizontalem oberem Ast}}\)

wobei:

_fyk Streckgrenze des Betonstahls nach DIN EN 1992-1-1, 3.2.3,

k das Verhältnis der Zugfestigkeit_ftk zur Streckgrenze, \(k = \frac{f_{tk}}{f_{yk}}\)

γs _ist der Teilsicherheitsbeiwert für Betonstahl

Die Verbundschubspannung wird unabhängig als das Verhältnis zwischen der durch FE-Analyse berechneten Verbundspannung _τb und der Verbundendfestigkeit _{fbd gemäß} DIN EN 1992-1-1, 8.4.2:

\[\frac{τ_{b}}{f_{bd}}\]

\[f_{bd} = 2,25 \cdot η_1\cdot η_2\cdot f_{ctd}\]

wobei:

_fctd ist der Bemessungswert der Betonzugfestigkeit nach DIN EN 1992-1-1, 3.1.6 (2). Wegen der zunehmenden Sprödigkeit von höherfestem Beton ist fctk_,0.05 auf den Wert für C60/75 nach DIN EN 1992-1-1 Cl. 8.4.2 (2)

_η1 ist ein Koeffizient, der von der Qualität des Verbundzustandes und der Lage des Stabes während des Betonierens abhängt (Abb. 31).

_η1 = 1,0, wenn "gute" Bedingungen erreicht werden und

_η1 = 0,7 für alle anderen Fälle und für Stäbe in Strukturelementen, die mit Gleitschalungen gebaut werden, es sei denn, es kann nachgewiesen werden, dass "gute" Verbundbedingungen bestehen

_η2 bezieht sich auf den Stabdurchmesser:

_η2 = 1,0 für Ø ≤ 32 mm

_η2 = (132 - Ø)/100 für Ø > 32 mm

\[ \textsf{\textit{\footnotesize{Abbildung 31: EN 1992-1-1 Abbildung 8.2 - Beschreibung der Verbundbedingungen}}}\]

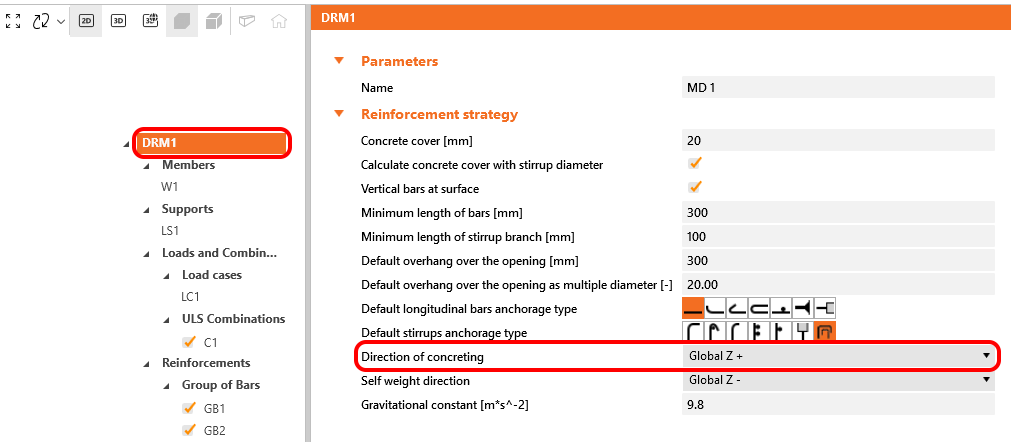
In IDEA StatiCa Detail werden die Verbundbedingungen gemäß Abb. 31 c) und d) berücksichtigt. Die Betonierrichtung kann in der Anwendung für jede Projektposition wie folgt eingestellt werden.

Diese Nachweise werden unter Berücksichtigung der entsprechenden Grenzwerte für die jeweiligen Teile des Bauwerks geführt (d.h. trotz einheitlicher Beton- und Bewehrungsgüte unterscheiden sich die endgültigen Spannungs-Dehnungs-Diagramme in jedem Teil des Bauwerks aufgrund von Zugversteifungs- und Druckentfestigungseffekten).

Gesamtkraft _Ftot und Grenzkraft _Flim

Die Gesamtkraft _Ftot ist ein Ergebnis der Finite-Elemente-Analyse und kann auf zwei Arten definiert werden.

\[F_{tot}=A_{s}\cdot \sigma_{s}\]

wobei_As die Fläche des Bewehrungsstabs und _σs die Spannung im Stab ist.

Oder als Summe aus der Verankerungskraft_{Fa und der} Verbundkraft _Fbond.

\[F_{tot}=F_{a}+F_{bond}\]

wobei_Fa die tatsächliche Kraft in der Verankerungsfeder und _Fbond die Verbundkraft ist, die durch Integration der Verbundspannung _τb über die Länge des Bewehrungsstabs l erhalten werden kann .

\[F_{bond}=C_{s} \cdot \int_{0}^{l}\tau_{b}\left( x \right)dx\]

_Cs ist der Umfang des Bewehrungsstabs.

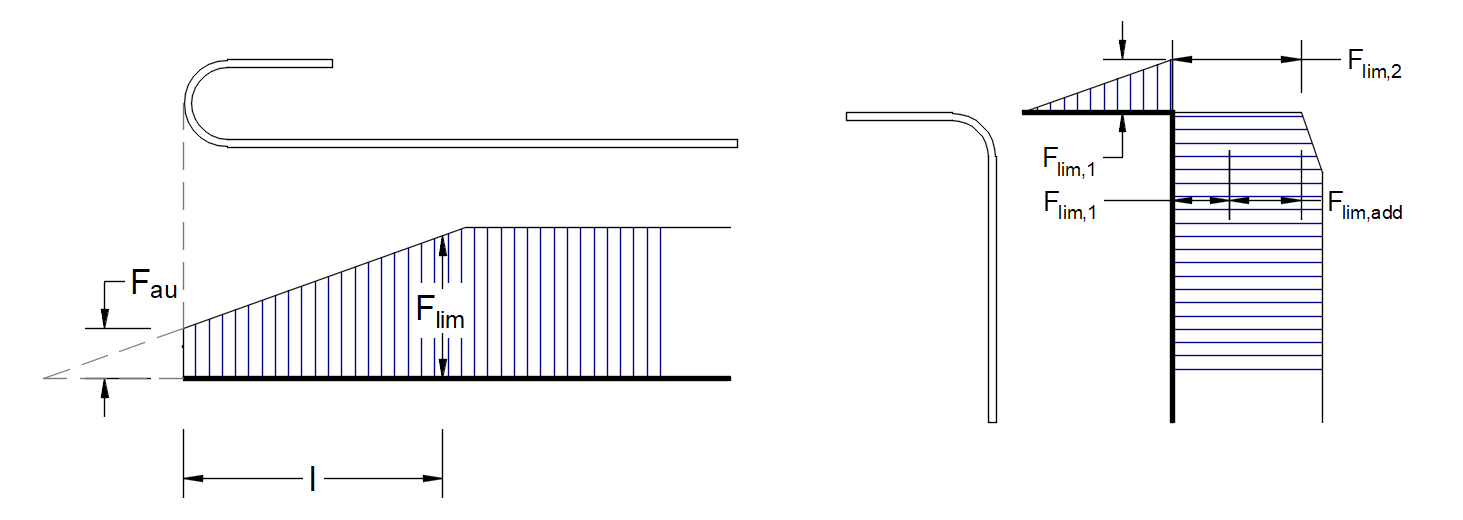
Die Grenzkraft_Flim ist die maximale Kraft im Element des Bewehrungsstabs unter Berücksichtigung der Tragfähigkeit des Bewehrungsstabs und der Verankerungsbedingungen (Verbund zwischen Beton und Bewehrung und Verankerungshaken, Schlaufen usw.).

\[F_{lim}=min\left( F_{lim,bond}+F_{au},F_{u} \right)\]

\[F_{u}=k\cdot f_{yd}\cdot A_{s}\]

\[F_{au}=\beta\cdot k\cdot f_{yd}\cdot A_{s}\]

\[F_{lim,bond}=C_{s}\cdot l \cdot f_{bd}\]

wobei _Cs der Umfang des Bewehrungsstabs und l die Länge vom Anfang des Bewehrungsstabs bis zum interessierenden Punkt ist.

\[ \textsf{\textit{\footnotesize{Fig. 32\qquad Definition der Grenzkraft Flim}}}\]

\[F_{lim,2}=F_{lim,1}+F_{lim,add}\]

wobei_Flim,add die zusätzliche Kraft ist, die aus der Größe des Winkels zwischen benachbarten Elementen berechnet wird._Flim,2 muss immer kleiner als_Fu sein.

Zu den verfügbaren Verankerungstypen im CSFM gehören ein gerader Stab (d. h. keine Reduzierung der Ankerenden), ein gebogener Stab, ein Haken, eine Schlaufe, ein geschweißter Querstab, ein perfekter Verbund und ein durchgehender Stab. Alle diese Typen sind zusammen mit den jeweiligen Verankerungsbeiwerten β in Abb. 32 für die Längsbewehrung und in Abb. 33 für die Bügel dargestellt. Die Werte der angenommenen Verankerungsbeiwerte entsprechen DIN EN 1992-1-1, 8.4.4 Tab. 8.2. Es ist zu beachten, dass das CSFM trotz der verschiedenen Möglichkeiten drei Arten von Verankerungsenden unterscheidet: (i) keine Verringerung der Verankerungslänge, (ii) eine Verringerung der Verankerungslänge um 30 % im Falle einer normalisierten Verankerung und (iii) perfekter Verbund.

\[ \textsf{\textit{\footnotesize{Verfügbare Verankerungsarten und ihre jeweiligen Verankerungsbeiwerte für Längsbewehrungsstäbe im CSFM.}}}\]

\[ \textsf{\textit{\footnotesize{(a) gerader Stab; (b) Biegung; (c) Haken; (d) Schlaufe; (e) geschweißter Querstab; (f) perfekte Verbindung; (g) durchgehender Stab.}}}\]

\[ \textsf{\textit{\footnotesize{Abbildung 33\qquad Verfügbare Verankerungstypen und entsprechende Verankerungskoeffizienten für Bügel.}}}\]

\[ \textsf{\textit{\footnotesize{Geschlossene Steigbügel: (a) Haken; (b) Biegung; (c) Überlappung. Offene Steigbügel: (d) Haken; (e) durchgehender Stab.}}}\]

Um DIN EN 1992-1-1 zu erfüllen, muss die Bewehrung immer mit geraden Enden modelliert werden und die Eigenschaft der Verankerung muss verwendet werden (Verankerungsfeder muss angewendet werden). Die Modellierung des Verankerungshakens durch direkte Änderung der Bewehrungsgeometrie ist nicht konform mit DIN EN 1992-1-1.

Teilbelastete Flächen

Bei der Bemessung von Betonstrukturen treffen wir auf zwei Arten der Bemessung der Teilflächenbelastung von Betonbauteilen - die Bemessung der Betondrucktragfähigkeit und die Ermittlung der erforderlichen Betonstahlmenge. Gemäß den derzeit geltenden Normen für die Stahlbetonbemessung (DIN EN 1992-1-1 Kap. 6.7, siehe Abb. 34) sollten lokales Betonversagen und Spaltzugkräfte berücksichtigt werden. Für eine gleichmäßig verteilte Last auf einer Fläche A_c0 kann die Druckkapazität von Beton je nach Bemessungsverteilungsfläche A_c1 um das max. Dreifache erhöht werden.

\[ \textsf{\textit{\footnotesize{Abb. 34\qquad Teilbelastete Flächen nach DIN EN 1992-1-1}}}\]

Die teilbelastete Fläche muss ausreichend mit einer Spaltzugbewehrung verstärkt sein, um die in dem Bereich auftretenden Querzugkräfte zu übertragen. Für die Bemessung der Spaltzugbewehrung in teilbelasteten Flächen wird die Fachwerkmethode nach Eurocode verwendet. Ohne die erforderliche Spaltzugbewehrung kann eine Erhöhung der Druckkapazität des Betons nicht in Betracht gezogen werden.

Teilbelastete Flächen in der CSFM

\[ \textsf{\textit{\footnotesize{Abb. 35\qquad Fiktive Streben mit Finite-Elemente-Netz aus Beton}}}\]

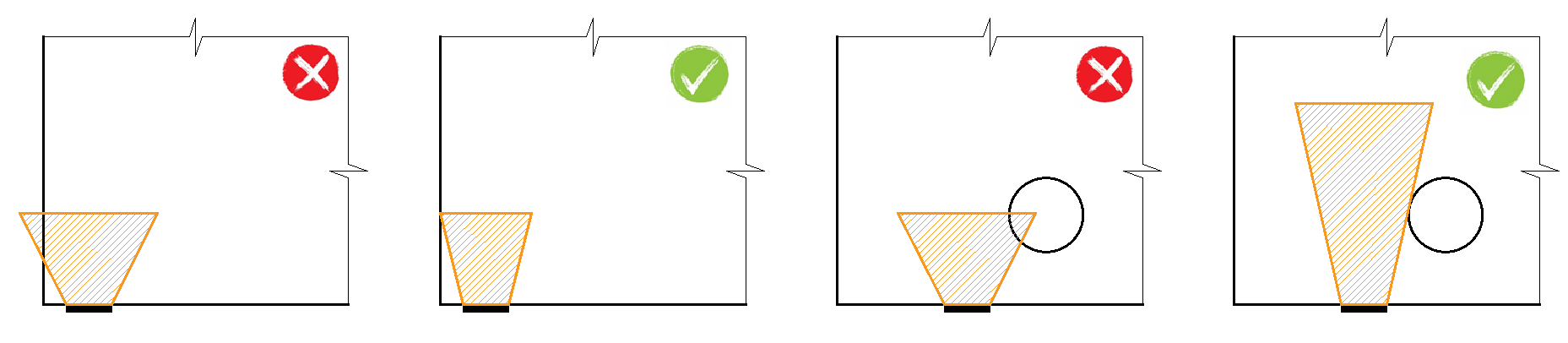
Mit der CSFM ist es möglich, bewehrte Betonstrukturen, unter Berücksichtigung des Einflusses der zunehmenden Druckfestigkeit von Beton in teilweise belasteten Bereichen, zu bemessen und zu bewerten. Da die CSFM ein Wandmodell (2D) ist und die teilbelasteten Fläche eine räumliche Aufgabe (3D) sind, musste eine Lösung gefunden werden, die diese beiden unterschiedlichen Aufgabentypen kombiniert (Abb. 35). Ist die Funktion „teilbelastete Flächen“ aktiviert, wird die zulässige Kegelgeometrie nach Eurocode erstellt (Abb. 34). Alle geometrischen Kollisionen werden vollständig in 3D für die festgelegte Geometrie des Betonbauteils und die Abmessungen jeder teilbelasteten Fläche gelöst. Anschließend wird ein Rechenmodell der teilbelasteten Fläche erstellt.

\[ \textsf{\textit{\footnotesize{Abb. 36\qquad Zulässige Kegelgeometrien}}}\]

Die Bearbeitung des Materialmodells erwies sich als ungeeigneter Ansatz, vor allem die Abbildung von Eigenschaften auf das Finite-Elemente-Netz problematisch ist. Es wurde festgestellt, dass ein vom Finite-Elemente-Netz unabhängiger Ansatz eine geeignetere Lösung ist. Für die bekannte Druckkegelgeometrie (Abb. 35 und Abb. 37) werden absolut kohärente fiktive Streben erzeugt (Abb. 35 und Abb. 37). Diese Streben haben identische Materialeigenschaften wie der im Modell verwendete Beton, einschließlich des Spannungs-Dehnungs-Diagramms. Die Form des Kegels bestimmt die Richtung der Streben, die die Last über die teilbelastete Fläche allmählich in den Verteilungsbereich verteilt. Die Flächendichte der fiktiven Streben ist an jedem Teil des Kegels veränderlich und fügt einen fiktiven Betonbereich in Lastrichtung hinzu. Auf der Ebene der belasteten Fläche (A_c0) wird eine fiktive Betonfläche gemäß dem Verhältnis \(\sqrt{A_{c0} \cdot A_{c1}} - A_{real}\) (mit A_real als Auflagerfläche im 2D-Computermodell) hinzugefügt, und dieser Bereich nimmt zur Bemessungsverteilungsfläche hin linear auf Null ab (A_c1). Diese Lösung stellt sicher, dass die Druckspannung im Beton über das gesamte Kegelvolumen konstant ist.

\[\rho \left( {\beta ,z} \right) = \left( {\sqrt {\frac{A_{c1}}{A_{c0}}}  - \frac{A_{real}}{A_{c0}}} \right)\,\cdot\,\left( {1 - \frac{z}{h}} \right)\,\cdot\,\frac{1}{{\cos \beta }}\]

\[ \textsf{\textit{\footnotesize{Abb. 37\qquad Fiktive Verstrebungen im Berechnungsmodell}}}\]

Die Tragfähigkeit der teilbelasteten Fläche wird entsprechend dem Verhältnis von Bemessungswert der verteilten Fläche zu belasteter Fläche gemäß DIN EN 1992-1-1 (6.7) erhöht. Es sei daran erinnert, dass dies eine Annahme darstellt, welche den Spannungszustand über einen teilbelasteten Bereich, dessen tatsächlicher Fluss viel komplizierter ist, nicht genau beschreiben kann. Diese Lösung ermöglicht jedoch die korrekte Lastverteilung auf das gesamte Modell unter Berücksichtigung der erhöhten Tragfähigkeit des teilbelasteten Bereichs. Des Weiteren werden in diesem Bereich Querzugspannungen korrekt eingeführt.

Quellen

ACI Committee 318. 2009a. Building Code Requirements for Structural Concrete (ACI 318-08) and Commentary. Farmington Hills, MI: American Concrete Institute.

Alvarez, Manuel. 1998. Einfluss des Verbundverhaltens auf das Verformungsvermögen von Stahlbeton. IBK Bericht 236. Basel: Institut für Baustatik und Konstruktion, ETH Zurich, Birkhäuser Verlag.

Beeby, A. W. 1979. “The Prediction of Crack Widths in Hardened Concrete.” The Structural Engineer 57A (1): 9–17.

Broms, Bengt B. 1965. “Crack Width and Crack Spacing In Reinforced Concrete Members.” ACI Journal Proceedings 62 (10): 1237–56. https://doi.org/10.14359/7742.

Burns, C. 2012. “Serviceability Analysis of Reinforced Concrete Members Based on the Tension Chord Model.” IBK Report Nr. 342, Zurich, Switzerland: ETH Zurich.

Crisfield, M. A. 1997. Non-Linear Finite Element Analysis of Solids and Structures. Wiley.

European Committee for Standardization (CEN). 2015. 1 Eurocode 2: Design of concrete structures - Part 1-1:  General rules and rules for buildings. Brussels: CEN, 2005.

Fernández Ruiz, M., and A. Muttoni. 2007. “On Development of Suitable Stress Fields for Structural Concrete.” ACI Structural Journal 104 (4): 495–502.

Kaufmann, W., J. Mata-Falcón, M. Weber, T. Galkovski, D. Thong Tran, J. Kabelac, M. Konecny, J. Navratil, M. Cihal, and P. Komarkova. 2020. “Compatible Stress Field Design Of Structural Concrete. Berlin, Germany.”AZ Druck und Datentechnik GmbH, ISBN 978-3-906916-95-8.

Kaufmann, W., and P. Marti. 1998. “Structural Concrete: Cracked Membrane Model.” Journal of Structural Engineering 124 (12): 1467–75. https://doi.org/10.1061/(ASCE)0733-9445(1998)124:12(1467).

Kaufmann, W.. 1998. “Strength and Deformations of Structural Concrete Subjected to In-Plane Shear and Normal Forces.” Doctoral dissertation, Basel: Institut für Baustatik und Konstruktion, ETH Zürich. https://doi.org/10.1007/978-3-0348-7612-4.

Konečný, M., J. Kabeláč, and J. Navrátil. 2017. Use of Topology Optimization in Concrete Reinforcement Design. 24. Czech Concrete Days (2017). ČBS ČSSI. https://resources.ideastatica.com/Content/06_Detail/Verification/Articles/Topology_optimization_US.pdf.

Marti, P. 1985. “Truss Models in Detailing.” Concrete International 7 (12): 66–73.

Marti, P. 2013. Theory of Structures: Fundamentals, Framed Structures, Plates and Shells. First edition. Berlin, Germany: Wiley Ernst & Sohn.

http://sfx.ethz.ch/sfx_locater?sid=ALEPH:EBI01&genre=book&isbn=9783433029916.

Marti, P., M.Alvarez, W. Kaufmann, and V. Sigrist. 1998. “Tension Chord Model for Structural Concrete.” Structural Engineering International 8 (4): 287–298.

https://doi.org/10.2749/101686698780488875.

Mata-Falcón, J. 2015. “Serviceability and Ultimate Behaviour of Dapped-End Beams (In Spanish: Estudio Del Comportamiento En Servicio y Rotura de Los Apoyos a Media Madera).” PhD thesis, Valencia: Universitat Politècnica de València.

Meier, H. 1983. “Berücksichtigung Des Wirklichkeitsnahen Werkstoffverhaltens Beim Standsicherheitsnachweis Turmartiger Stahlbetonbauwerke.” Institut für Massivbau, Universität Stuttgart.

Navrátil, J., P. Ševčík, L. Michalčík, P. Foltyn, and J. Kabeláč. 2017. A Solution for Walls and Details of Concrete Structures. 24. Czech Concrete Days.

Schlaich, J., K. Schäfer, and M. Jennewein. 1987a. “Toward a Consistent Design of Structural Concrete.” PCI Journal 32 (3): 74–150.

Vecchio, F.J., and M.P. Collins. 1986. “The Modified Compression Field Theory for Reinforced Concrete Elements Subjected to Shear.” ACI Journal 83 (2): 219–31.

Anhänge zum Download

• Theoretical Background 20.pdf (PDF, 2,1 MB)