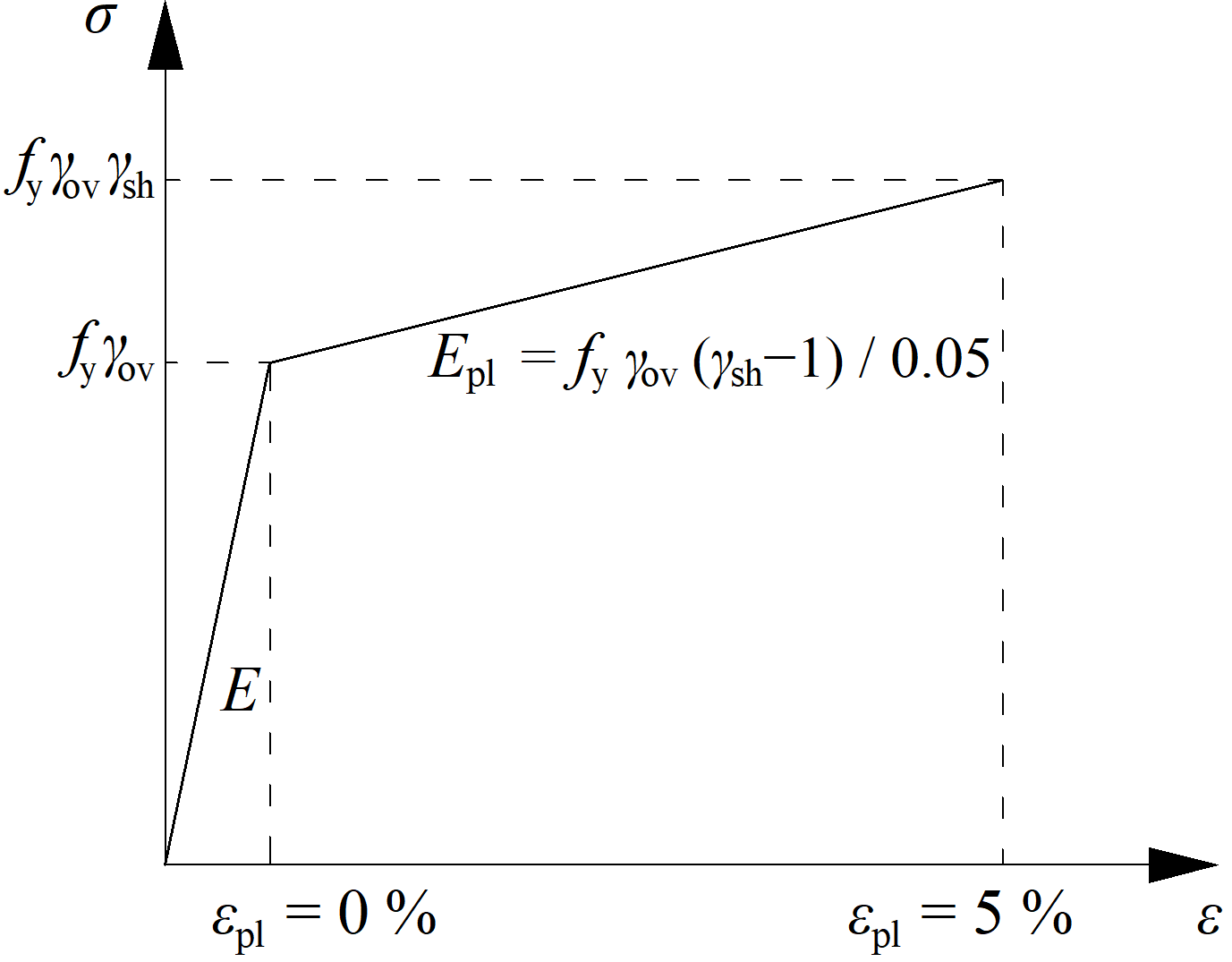Nachweis von Komponenten nach EN (Eurocode)
Die CBFEM-Methode kombiniert die Vorteile der allgemeinen Finite-Elemente-Methode (FEM) und der Standardkomponentenmethode (CM). Die anhand des genauen CBFEM-Modells berechneten Spannungen und Schnittgrößen werden beim Nachweis aller Komponenten verwendet.
Einzelne Komponenten werden nach Eurocode EN 1993-1-8 nachgewiesen.
Nachweis von Platten nach Eurocode
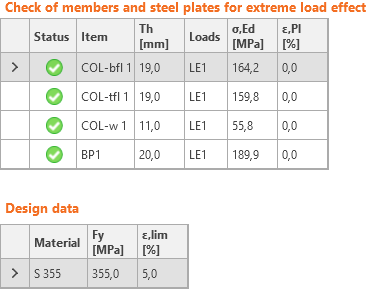
Die resultierende Vergleichsspannung (Huber-Mises-Hencky – HMH, von Mises) und die plastische Dehnung werden auf Platten berechnet. Für Stahlplatten wird ein elasto-plastisches Materialmodell verwendet. Es wird ein Nachweis einer äquivalenten plastischen Dehnung durchgeführt. Der Grenzwert von 5% wird im Eurocode empfohlen (EN 1993-1-5, Anh. C, Abs. C8, Anmerkung 1), dieser Wert kann vom Nutzer in den Normeinstellungen geändert werden.
Das Plattenelement wird in 5 Ebenen unterteilt und das elastische/plastische Verhalten wird in jeder Ebene separat untersucht. Die Übersicht der Ausgabe listet den kritischsten Nachweis aus allen 5 Ebenen auf.
Die CBFEM-Methode kann Spannungen ausgeben, die eher höher sind als die Streckgrenze. Der Grund ist die leichte Neigung des plastischen Zweigs des Spannungs-Dehnungs-Diagramms, das in der Berechnung zur Verbesserung der Stabilität der Interaktionsrechnung verwendet wird. Dies ist für die praktische Bemessung kein Problem. Bei höheren Belastungen steigt die äquivalente plastische Dehnung an und die Verbindung versagt bei Überschreitung der plastischen Dehngrenze.
Nachweis von Schweißnähten nach Eurocode
Kehlnähte werden nach EN 1993-1-8 nachgewiesen. Die Tragfähigkeit von Stumpfnähten wird als die des Schweißguts angenommen und nicht nachgewiesen.
Kehlnähte
Bemessungstragfähigkeit
Die plastische Umverteilung in Schweißnähten wird verwendet, um die Spannungssingularitäten in Schweißnahtelementen automatisch zu vermeiden und die Spannung entlang der Schweißnahtlänge umzuverteilen. Die Festigkeit der Schweißnaht entspricht in etwa der Handberechnung und die Spannung wird bei komplizierten Problemen wie dem Verschweißen an nicht versteiften Flanschen korrekt verteilt (EN 1993-1-8, Abs. 4. Die Spannung im Halsbereich einer Kehlnaht wird nach EN 1993-1-8, Abs. 4.5.3 ermittelt. Die Spannungen werden aus den Spannungen im Schweißnahtelement berechnet. Das Biegemoment um die Längsachse der Schweißnaht wieder nicht berücksichtigt.
\[ \sigma_{w,Ed}=\sqrt{\sigma_{\perp}^2 + 3 \left ( \tau_{\perp}^2 + \tau_{\parallel}^2 \right )} \]
\[ \sigma_{w,Rd} = \frac{f_u}{\beta_w \gamma_{M2}} \]
Ausnutzung der Schweißnaht
\[ U_t = \min \left\{ \frac{\sigma_{{w,Ed}}}{\sigma_{w,Rd}}, \frac{\sigma_{\perp}}{0.9 f_u / {\gamma_{M2}}} \right\} \]
wo:
- σw,Ed – Vergleichsspannugn in der Schweißnaht
- σw,Rd – Schweißnahtwiderstand
- βw – Korrelationsfaktor (EN 1993-1-8 – Tabelle 4.1)
- fu – Zugfestigkeit, gewählt als das untere der beiden verbundenen Grundmaterialien oder je nach vom Benutzer gewähltem Material
- γM2 – Sicherheitsfaktor (EN 1993-1-8 – Tabelle 2.1; änderbar in den Normeinstellungen)
- σ┴, τ┴, τ‖ – Spannungen in der Schweißnaht gemäß der folgenden Abbildung:
Alle für den Nachweis erforderlichen Werte werden in Tabellen ausgegeben. Ut ist die Auslastung des am meisten belasteten Schweißnahtelements. Da eine plastische Umverteilung der Spannung in der Schweißnaht verwendet wird, ist dies die entscheidende Ausnutzung. Utc gibt Informationen zur Ausnutzung entlang der Schweißnahtlänge wieder; es ist definiert als das Verhältnis der Spannung des am meisten belasteten Schweißnahtelements innerhalb der jeweiligen Schweißnaht zur Bemessungstragfähigkeit der Spannung der gesamten Schweißnahtlänge.
Die Vergleichsspannung im Schweißnahtdiagramm zeigt folgende Spannung:
\[ \sigma = \max \left \{ \frac{\sigma_{\perp}}{0.9 \beta_w}, \, \sqrt{\sigma_{\perp}^2 + 3 \tau_{\perp}^2 + 3 \tau_{\parallel}^2} \right \} \]
Stumpfähte
Es wird eine vollständige Durchdringung des Anschlusses angenommen, weshalb diese Schweißnähte nicht nachgewiesen werden.
Nachweis von Schrauben und vorgespannten Schrauben nach Eurocode
Schrauben
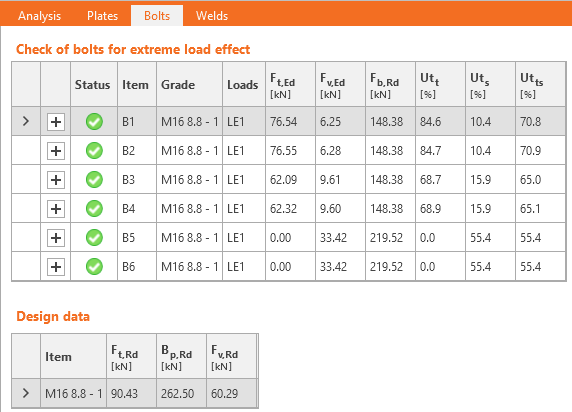
Die Anfangssteifigkeit und die Bemessungstragfähigkeit von Schrauben bei Schub werden in CBFEM nach Abs. 3.6 und 6.3.2 in EN 1993-1-8 wiedergegeben. Die Feder, die Lochleibung und Zug darstellen, hat ein bilineares Kraft-Verformungs-Verhalten mit einer Anfangssteifigkeit und einer Bemessungstragfähigkeit nach Abs. 3.6 und 6.3.2 in EN 1993-1-8.
Bemessungswert der Zugtragfähigkeit der Schraube (EN 1993-1-8 – Tabelle 3.4):
\[ F_{t,Rd}=0,9 f_{ub} A_s / \gamma_{M2} \]
Bemessungswert der Durchstanztragfähigkeit des Schraubenkopfes oder der Schraubenmutter (EN 1993-1-8 – Tabelle 3.4):
\[ B_{p,Rd} = 0,6 \pi d_m t_p f_u / \gamma_{M2} \]
Bemessungswert der Schertragfähigkeit je Scherebene (EN 1993-1-8 – Tabelle 3.4):
\[ F_{v,Rd} = \alpha_v f_{ub} A_s / \gamma_{M2} \]
Die Bemessungsschubtragfähigkeit kann mit dem Reduktionsfaktor βp multipliziert werden, wenn ein Versatz vorhanden ist (EN 1993-1-8 – Abs. 3.6.1. (12)) und diese Option in den Normeinstellungen ausgewählt ist.
Bemessungswert der Lochleibungstragfähigkeit der Platte (EN 1993-1-8 – Tabele 3.4):
\( F_{b,Rd} = k_1 a_b f_u d t / \gamma_{M2} \) für Standardlöcher
\( F_{b,Rd} = 0,6 k_1 a_b f_u d t / \gamma_{M2} \) für Langlöcher
Ausnutzung bei Zug [%]:
\[ Ut_t = \frac{F_{t,Ed}}{\min (F_{t,Rd},\, B_{p,Rd})} \]
Ausnutzung bei Schub [%]:
\[ Ut_t = \frac{V}{\min (F_{v,Rd},\, F_{b,Rd})} \]
Interaktion von Zug und Schub [%]:
\[ Ut_{ts}=\frac{V}{F_{v,Rd}}+\frac{F_{t,Ed}}{1,4 F_{t,Rd}} \]
Wo:
- As – Zugspannungsfläche der Schraube
- fub – Zugfestigkeit der Schraube
- dm – Mittelwert der Schnittpunkte und Schlüsselweiten des Schraubenkopfes oder der Mutter, je nachdem, welcher Wert kleiner ist
- d – Schraubendurchmesser
- tp – Plattendicke unter dem Schraubenkopf/-mutter
- fu – Stahlfestigkeit
- αv = 0,6 für die Klasse 4.6, 5.6, 8.8 and 0,5 für die Klassen 4.8, 5.8, 6.8, 10.9
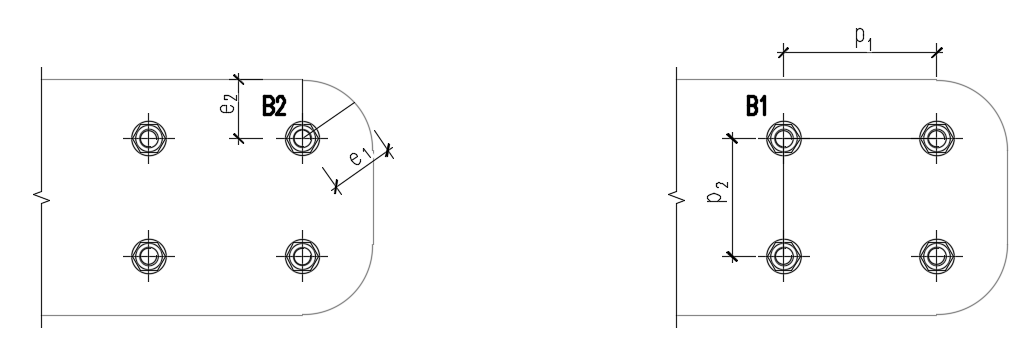
- \( k_1 = \min \left (2,8 \frac{e_2}{d_0}-1,7, \, 1,4 \frac{p_2}{d_0}-1,7, \, 2,5 \right ) \) – Faktor aus Tabelle 3.4
- αb = 1,0 wenn der Lochleibungsnachweis mit ab in den Normeinstellungen deaktiviert ist; bei aktiviertem Nachweis wird der Wert für αb nach EN 1993-1-8 – Tabelle 3.4 ermittelt: \( \alpha_d = \min \left ( \frac{e_1}{3 d_0}, \, \frac{p_1}{3 d_0}-\frac{1}{4}, \, \frac{f_{ub}}{f_u} \right ) \)
- e1, e2 – Kantenabstände in Lastrichtung und senkrecht zur Lastrichtung
- p1, p2 – Schraubenabstände in Lastrichtung und senkrecht zur Lastrichtung
- Ft,Ed – Zugkraft (Bemessungswert) in der Schraube
- V – Scherkraft (Bemessungswert) in der Schraube
- γM2 – Sicherheitsfaktor (EN 1993-1-8 – Tabelle 2.1; änderbar in den Normeinstellungen)
Randabstände, die für die Schraubentragfähigkeit verwendet werden, müssen für allgemeine Plattengeometrien, Platten mit Öffnungen, Ausschnitten usw. relevant sein.
Der Algorithmus liest die tatsächliche Richtung des resultierenden Schubkraftvektors in einer gegebenen Schraube und berechnet dann die Abstände, die für den Lochleibungsnachweis benötigt werden.
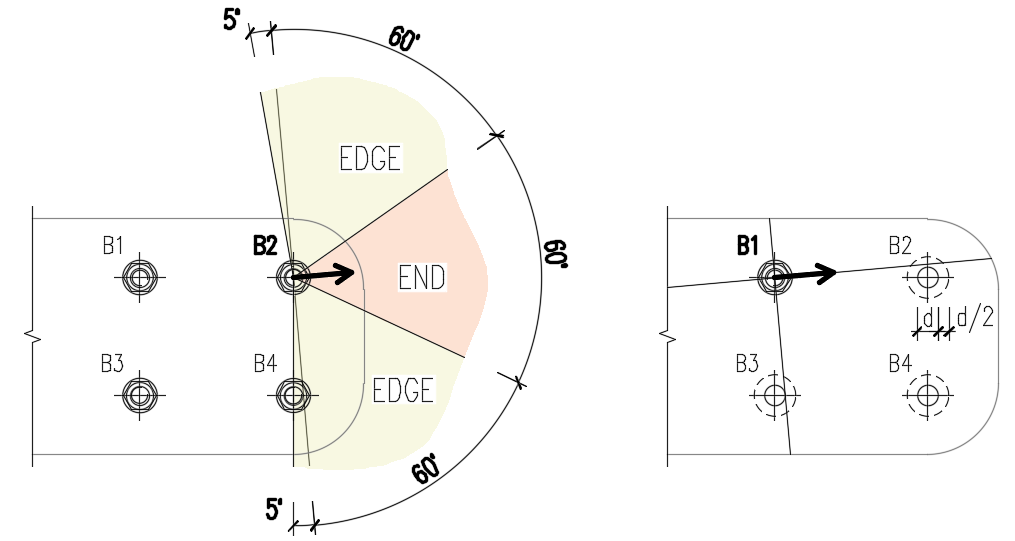
Die End- (e1) und Randabstände (e2) werden durch Aufteilen der Plattenkontur in drei Segmente bestimmt. Das Endsegment ist durch einen 60°-Bereich in Richtung des Kraftvektors gekennzeichnet. Die Kantensegmente werden durch zwei 65°-Bereiche senkrecht zum Kraftvektor definiert. Als End- oder Kantenabstand wird dann der kürzeste Abstand einer Schraube zu einem relevanten Segment genommen.
Die Abstände zwischen den Schraubenlöchern (p1; p2) werden ermittelt, indem die umgebenden Schraubenlöcher virtuell um die Hälfte ihres Durchmessers vergrößert werden und dann zwei Linien in Richtung und senkrecht zum Schubkraftvektor gezogen werden. Die Abstände zu den vergrößerten Schraubenlöchern, die von diesen Linien geschnitten werden, gehen dann als p1 und p2 in die Berechnung ein.
Vorgespannte Schrauben
Bemessungswert des Gleitwiderstand je Schraubenklasse 8.8 oder 10.9 (EN 1993-1-8, Abs. 3.9 – Gleichung 3.8):
\[ F_{s,Rd} =\frac{k_s n \mu (F_{p,C} - 0,8 F_{t,Ed})}{\gamma_{M3}} \]
Die Vorspannkraft (EN 1993-1-8 – Gleichung 3.7)
Fp,C = 0,7 fub As
Der Vorspannkraftfaktor 0,7 kann in den Normeinstellungen geändert werden.
Ausnutzung [%]:
\[ Ut_s = \frac{V}{F_{s,Rd}} \]
Wo:
- As – Zugspannungsfläche der Schraube
- fub – Zugfestigkeit
- ks – Koeffizient (EN 1993-1-8 – Tabelle 3.6; ks = 1 für normale Rundlöcher, ks = 0,63 für Langlöcher)
- μ – Gleitfaktor, änderbar in den Normeinstellungen (EN 1993-1-8 – Tabelle 3.7)
- n – Anzahl der Reibflächen. Der Nachweis wird für jede Reibfläche separat berechnet
- γM3 – Sicherheitsfaktor (EN 1993-1-8 – Tabelle 2.1; änderbar in den Normeinstellungen – empfohlene Werte sind 1,25 für den Grenzzustand der Tragfähigkeit und 1,1 für den Nachweis im Grenzzustand der Gebrauchstauglichkeit)
- V – Scherkraft (Bemessungswert) in der Schraube
- Ft,Ed – Zugkraft (Bemessungswert) in der Schraube
Wird das Gleiten von vorgespannten Schrauben im Grenzzustand der Gebrauchstauglichkeit überprüft, sollten diese anschließend auf "Lochleibung - Interaktion Scherzug" umgestellt und auf den Grenzzustand der Tragfähigkeit überprüft werden.
Konstruktionsregeln
Das Überprüfen der Konstruktionsregeln von Schrauben wird durchgeführt, wenn die Option in den Normeinstellungen ausgewählt ist. Überprüft werden die Abmessungen von der Schraubenmitte zu den Plattenkanten und zwischen den Schrauben. Randabstand e = 1,2 und Schraubenabstand p = 2,2 werden in Tabelle 3.3 in EN 1993-1-8 empfohlen. Der Anwender kann beide Werte in den Normeinstellungen ändern.
Nachweis von Ankern gemäß Eurocode
Die Tragfähigkeiten der Ankerschraube werden nach EN 1992-4, Abs. 7.2 für Kopf- und nachträglich montierte Anker ausgewertet. Auszugsversagen von geraden Ankern, kombiniertes Auszugs- und Betonversagen von Verbundankern und Betonspaltversagen werden aufgrund fehlender Informationen, die nur für den jeweiligen Anker- und Klebetyp des Ankerherstellers vorliegen, nicht geprüft.
In den Normeinstellungen sind Einstellungen zum De-/Aktivieren von Nachweisen des Betonkegelausbruchs bei Zug und Schub verfügbar. Ist der Nachweis des Betonkegelbruchs nicht aktiviert, wird davon ausgegangen, dass die Bewehrung so ausgelegt ist, dass sie der Kraft standhält. Die Größe der Kraft wird in Formeln angegeben. Darüber hinaus kann der Beton gerissen oder ungerissen eingestellt werden. Die Tragfähigkeiten von ungerissenem Beton sind höher.
Zugtragfähigkeit des Stahl (EN 1992-4, Abs. 7.2.1.3):
\[ N_{Rd,s} = \frac{N_{Rk,s}}{\gamma_{Ms}} \]
Wo:
- NRk,s = c ∙ As ∙ fuk – Charakteristische Tragfähigkeit eines Anekrs bei Stahlversagen
- c – Abnahme der Zugfestigkeit von Schrauben mit geschnittenem Gewinde nach EN 1993-1-8 – Abs. 3.6.1. (3); änderbar in den Normeinstellungen
- As – Zugspannungsfläche der Ankerschraube
- fuk – Charakteristische Zugfestigkeit der Ankerschraube
- \(\gamma_{Ms}=1,2 \cdot \frac{f_{uk}}{f_{yk}} \ge 1,4\) – Teilsicherheitsfaktor für Stahlversagen bei Zug (EN 1992-4, Tabelle 4.1)
- fyk – Charakteristische Streckgrenze der Ankerschraube
Betonkegelfestigkeit für Versagen eines Ankers oder einer Ankergruppe (EN 1992-4, Abs. 7.2.1.4):
\[ N_{Rd,c} = \frac{N_{Rk,c}}{\gamma_{Mc}} \]
Wo:
- \(N_{Rk,c}=N_{Rk,c}^0 \cdot \frac{A_{c,N}}{A_{c,N}^0} \cdot \psi_{s,N} \cdot \psi_{re,N} \cdot \psi_{ec,N} \cdot \psi_{M,N}\) – Charakteristische Tragfähigkeit eines Ankers, einer Ankergruppe und der auf Zug belasteten Anker einer Ankergruppe bei Betonkegelversagen
- \(N_{Rk,c}^0 = k_1 \sqrt{f_{ck}} h_{ef}^{1,5}\) – Charakteristische Tragfähigkeit eines einzelnen im Beton angebrachten Ankers, der nicht durch benachbarte Anker oder Kanten des Betonbauteils beeinflusst wird
- k1 – Faktor zur Berücksichtigung des Betonzustands und des Ankertyps; für eingegossene Kopfanker (mit Kopfplatten) k1 = 8,9 für gerissenen Beton und k1 = 12,7 für ungerissenen Beton; für nachträglich angebrachte Anker (gerade Anker) k1 = 7,7 für gerissenen Beton und k1 = 11,0 für ungerissenen Beton
- fck – Charakteristische Betondruckzylinderfestigkeit
- hef – Einbettungstiefe des Anker im Beton; für 3 oder mehr nahe Kanten wird EN 1992-4, Abs. 7.2.1.4 (8) und das wirksame \(h'_{ef} = \max \left \{ \frac{c_{max}}{c_{cr,N}} \cdot h_{ef}, \, \frac{s_{max}}{s_{cr,N}} \cdot h_{ef} \right \}\) in den Formeln für NRk,c0, ccr,N, scr,N, Ac,N, Ac,N0, ψs,N, und ψec,N verwendet
- Ac,N – Tatsächliche projizierte Fläche, begrenzt durch überlappende Betonkegel benachbarter Anker sowie durch Kanten des Betonbauteils
- Ac,N0 = scr,N2 – Projizierte Bezugsfläche, d.h. die Betonfläche eines einzelnen Ankers mit großem Abstand und Kantenabstand an der Betonoberfläche
- \(\psi_{s,N}=0,7+0,3 \cdot \frac{c}{c_{cr,N}} \le 1\) – Faktor zur Berücksichtigung der Störung der Spannungsverteilung im Beton durch die Nähe einer Kante des Betonbauteils
- c – Kleinster Kantenabstand
- ccr,N = 1,5 ∙ hef – Charakteristischer Kantenabstand zur Sicherstellung der Übertragung der charakteristischen Tragfähigkeit eines Ankers bei Betonausbruch unter Zugbelastung
- \(\psi_{re,N}=0,5+\frac{h_{ef}}{200} \le 1\) – Schalenabplatzungsfaktor
- \(\psi_{ec,N}=\frac{1}{1+2 \cdot (e_N / s_{cr,N})} \le 1\) – Faktor zur Berücksichtigung der Gruppenwirkung, wenn unterschiedliche Zugbelastungen auf die einzelnen Anker einer Gruppe wirken; ψec,N wird für jede Richtung separat bestimmt und das Produkt beider Faktoren verwendet
- eN – Exzentrizität der resultierenden Zugkraft der auf Zug belasteten Anker in Bezug auf den Schwerpunkt der auf Zug belasteten Anker
- scr,N = 2 ∙ ccr,N – Charakteristischer Ankerabstand zur Sicherstellung der charakteristischen Tragfähigkeit der Anker bei Betonkegelbruch unter Zugbelastung
- \(\psi_{M,N} = 2- \frac{z}{1.5 \cdot h_{ef}} \ge 1\) – Faktor zur Berücksichtigung einer Druckkraft zwischen Fixierung und Beton bei Biegemomenten mit oder ohne Normalkraft; dieser Parameter ist gleich 1, wenn c < 1,5 hef oder das Verhältnis der Druckkraft (einschließlich von Druck durch Biegung) zur Summe der Zugkräfte in den Ankern kleiner als 0,8 ist oder z / hef ≥ 1,5
- z – Innerer Hebelarm des Ankers
- γMc = γc ∙ γinst – Teilsicherheitsfaktor (EN 1992-4, Tabelle 4.1)
- γc – Teilsicherheitsfaktor für Beton (änderbar in den Normeinstellungen)
- γinst – Teilsicherheitsfaktor taking account of the installation safety of an anchor system (änderbar in den Normeinstellungen)
Die Betonausbruchskegelfläche für eine Gruppe von auf Zug belasteten Ankern, die einen gemeinsamen Betonkegel Ac,N bilden, ist durch eine rote gestrichelte Linie dargestellt.
Auszugsfestigkeit (EN 1992-4, Abs. 7.2.1.5)
Die Auszugsfestigkeit wird bei Ankern mit Kopfplatten nach EN 1992-4, Abs. 7.2.1.5 nachgewiesen:
\[ N_{Rd,p}=\frac{N_{Rk,p}}{\gamma_{Mc}} \]
Wo:
- NRk,p = k2 ∙ Ah ∙ fck – Charakteristische Tragfähigkeit bei Auszugsversagen
- k2 – Beiwert abhängig vom Betonzustand, k2 = 7,5 für gerissenen Beton, k2 = 10,5 für ungerissenen Beton
- Ah – Auflagefläche des Ankerkopfes; für runde Kopfplatten \(A_h = \frac{\pi}{4} \left ( d_h^2 - d^2 \right )\), für rechteckige Kopfplatten \(A_h = a_{wp}^2 - \frac{\pi}{4} d^2\)
- dh ≤ 6 th + d – Kopfdurchmesser des Kopfankers
- th – Kopfdicke des Kopfankers
- d – Durchmesser des Ankerschafts
- fck – Charakteristische Betondruckzylinderfestigkeit
- γMc = γc ∙ γinst – Teilsicherheitsfaktor (EN 1992-4, Tabelle 4.1)
- γc – Teilsicherheitsfaktor für Beton (änderbar in den Normeinstellungen)
- γinst – Teilsicherheitsfaktor zur Berücksichtigung der Montagesicherheit eines Ankersystems(änderbar in den Normeinstellungen)
Die Auszugsfestigkeit anderer Ankertypen wird nicht nachgewiesen und muss vom Hersteller garantiert werden.
Betonausbruchfestigkeit (EN 1992-4, Abs. 7.2.1.8)
Ausbruchversagen wird bei Kopfankern (Ankertyp – Kopfplatte) mit Randabstand c ≤ 0,5 hef nach EN 1992-4, Abs. 7.2.1.8 nachgewiesen. Anker werden als Gruppe behandelt, wenn ihr Abstand in Kantennähe s ≤ 4 c1 beträgt. Hinterschnittanker können auf die gleiche Weise nachgewiesen werden, aber der Wert von Ah ist in der Software unbekannt. Das Ausbruchversagen von Hinterschnittankern kann durch Auswahl von Kopfplatten mit entsprechender Abmessung ermittelt werden.
\[N_{Rd,cb} = \frac{N_{Rk,cb}}{\gamma_{Mc}}\]
Wo:
- \(N_{Rk,cb} = N_{Rk,cb}^0 \cdot \frac{A_{c,Nb}}{A_{c,Nb}^0} \cdot \psi_{s,Nb} \cdot \psi_{g,Nb} \cdot \psi_{ec,Nb}\) – Charakteristische Tragfähigkeit bei Betonausbruchversagen
- \(N_{Rk,cb}^0 = k_5 \cdot c_1 \cdot \sqrt{A_h} \cdot \sqrt{f_{ck}}\) – Charakteristische Tragfähigkeit eines einzelnen Ankers, unbeeinflusst durch benachbarte Anker oder weitere Kanten
- Ac,Nb – Tatsächliche projizierte Fläche, begrenzt durch überlappende Betonausbruchkörper benachbarter Anker sowie durch Kantennähe des Betonbauteils oder die Bauteildicke
- Ac,Nb0 = (4 c1)2 – Projizierte Bezugsfläche eines einzelnen Ankers mit einem Kantenabstand von c1
- \(\psi_{s,Nb} = 0,7+0,3 \frac{c_2}{2 c_1} \le 1\) – Faktor zur Berücksichtigung der Störung der Spannungsverteilung im Beton aufgrund der Nähe einer Ecke des Betonbauteils
- \( \psi_{g,Nb} = \sqrt{n} + (1-\sqrt{n}) \frac{s_2}{4c_1} \ge 1 \) – Faktor zur Berücksichtigung der Gruppenwirkung
- \(\psi_{ec,Nb} = \frac{1}{1+2 e_N / s_{cr,Nb}} \le 1\) – Faktor zur Berücksichtigung der Gruppenwirkung, wenn unterschiedliche Lasten auf die einzelnen Anker einer Gruppe wirken
- k5 – Parameter bezogen auf den Betonzustand; für gerissenen Beton k5 = 8,7, für ungerissenen Beton k5 = 12,2
- c1 – Kantenabstand des Ankers in Richtung 1 zur nächsten Kante
- c2 – Kantenabstand des Ankers senkrecht zur Richtung 1: Der kleinste Kantenabstand in einem schmalen Bauteil mit mehreren Kantenabständen
- Ah – Fläche des Last tragenden Ankerkopfes; für kreisförmige Kopfplatten \(A_h = \frac{\pi}{4} \left ( d_h^2 - d^2 \right )\), für rechteckige Kopfplatten \(A_h = a_{wp}^2 - \frac{\pi}{4} d^2\)
- d – Nomineller Ankerdurchmesser
- dh – Durchmesser der kreisförmigen Kopfplatte
- awp – Seitengröße der quadratischen Kopfplatte
- fck – Charakteristische Zylinderdruckfestigkeit von Beton
- n – Anzahl an in einer Reihe parallelen Anker zur Kante des Betonbauteils
- s2 – Abstand der Anker in einer Gruppe senkrecht zur Richtung 1
- scr,Nb = 4 c1 – Erforderlicher Abstand, damit ein Anker seine charakteristische Zugfestigkeit gegen Ausbruchversagen entwickeln kann
Scherfestigkeit des Ankerstahls (EN 1992-4 – Abs. 7.2.2.3)
Die Schertragfähigkeit von Ankerstahl wird nach EN 1992-4 – Abs. 7.2.2.3 nachgewiesen. Reibung wird nicht berücksichtigt. Scherung mit und ohne Hebelarm wird in Abhängigkeit von den Einstellungen der Fertigungsoperation der Fußplatte erkannt.
\[V_{Rd,s} = \frac{V_{Rk,s}}{\gamma_{Ms}}\]
Für Abstand: direkt, Scherung wird ohne Hebelarm angenommen (EN 1992-4 – Abs. 7.2.2.3.1):
VRk,s = k6 ∙ As ∙ fuk – Charakteristische Tragfähigkeit eines einzelnen Ankers bei Stahlversagen; oder bei Ankern mit einem Verhältnis hef/dnom < 5 und einer Betondruckfestigkeitsklasse < C20/25 ist die charakteristische Tragfähigkeit VRk,s mit dem Faktor 0,8 zu multiplizieren.
Für Abstand: Mortelfuge, Scherung wird mit Hebelarm angenommen (EN 1992-4 – Abs. 7.2.2.3.2):
\[V_{Rk,s}= \frac{\alpha_M \cdot M_{Rk,s}}{l_a}\]
Wo:
- k6 = 0,6 für Anker mit fuk ≤ 500 MPa; ansonsten k6 = 0,5
- As – Scherfläche des Ankers; wird Scherebene im Gewinde gewählt, wird die durch das Gewinde reduzierte Fläche verwendet; andernfalls wird die gesamte Schaftfläche verwendet
- fuk – Zugfestigkeit der Ankerschraube
- αM = 2 – Annahme einer vollen Einspannung (EN 1992-4 – Abs. 6.2.2.3)
- \( M_{Rk,s} = M_{Rk,s}^0 \left ( 1 - \frac{N_{Ed}}{N_{Rd,s}} \right ) \) – Charakteristische Biegetragfähigkeit des Ankers vermindert um die Zugkraft im Anker
- MRk,s0 = 1,2 Wel fub – Charakteristische Biegetragfähigkeit des Ankers (ETAG 001, Anhang C – Gleichung (5.5b))
- \( W_{el} = \frac{\pi d^3}{32}\) – Widerstandsmoment des Ankers
- d – Durchmesser der Ankerschraube; wenn Scherebene im Gewinde gewählt wird, wird der um Gewinde reduzierte Durchmesser verwendet; andernfalls wird der nominelle Durchmesser dnom verwendet
- NEd – Zugkraft im Anker
- NRd,s – Zugtragfähigkeit des Ankers
- la = 0,5 dnom + tmortar + 0,5 tbp – Hebelarm
- tmortar – Dicke der Mörtelschicht
- tbp – Dicke der Fußplatte
- γMs = 1,0 ∙ fuk / fyk ≥ 1,25 für fuk ≤ 800 MPa und fyk / fuk ≤ 0,8; ansonsten γMs = 1,5 – Teilsicherheitsfaktor für Stahlversagen (EN 1992-4 – Tabelle 4.1)
Betonausbruchversagen (EN 1992-4 – Abs. 7.2.2.4):
\[ V_{Rd,cp}= \frac{V_{Rk,cp}}{\gamma_{Mc}} \]
Wo:
- VRk,cp = k8 ∙ NRk,c – Charakteristische Tragfähigkeit bei Betonausbruchversagen
- k8 = 1 für hef < 60 mm; k8 = 2 für hef ≥ 60 mm (ETAG 001, Anhang C – Abs. 5.2.3.3)
- NRk,c – Charakteristische Tragfähigkeit eines Ankers, einer Anekrgruppe und der auf Zug belasteten Anker einer Ankergruppe bei Betonkonusbruch; es wird davon ausgegangen, dass alle Anker auf Zug belastet werden
- γMc = γc – Teilsicherheitsfaktor (EN 1992-4 – Tabelle 4.1, γinst = 1,0 für Scherlasten)
- γc – Teilsicherheitsfaktor für Beton (änderbar in den Normeinstellungen)
Betonkantenversagen (EN 1992-4 – Abs. 7.2.2.5):
Betonkantenversagen ist ein sprödes Versagen und es wird der ungünstigste Fall geprüft, d.h. nur die kantennahen Anker übertragen die volle Scherlast auf eine gesamte Fußplatte. Bei rechtwinkliger Anordnung der Anker überträgt die Ankerreihe an der untersuchten Kante die Scherlast. Sind die Anker unregelmäßig positioniert, übertragen die beiden der untersuchten Kante am nächsten liegenden Anker die Scherlast. Es werden zwei Kanten in Richtung der Scherlast untersucht und der "Worst Case" im Ergebnis dargestellt.
Untersuchte Kanten in Abhängigkeit von der Richtung der resultierenden Scherkraft
\[ V_{Rd,c} = \frac{V_{Rk,c}}{\gamma_{Mc}} \]
Wo:
- \( V_{Rk,c}= V_{Rk,c}^0 \cdot \frac{A_{c,V}}{A_{c,V}^0} \cdot \psi_{s,V} \cdot \psi_{h,V} \cdot \psi_{ec,V} \cdot \psi_{\alpha,V} \cdot \psi_{re,V} \) – Charakteristische Tragfähigkeit eines Anker oder einer Ankergruppe, die zur Kante hin belastet wird
- \( V_{Rk,c}^0 = k_9 \cdot d_{nom}^\alpha \cdot l_f^\beta \cdot f_{ck}^{0.5} \cdot c_1^{1.5}\) – Anfangswert der charakteristischen Tragfähigkeit eines senkrecht zur Kante belasteten Ankers
- k9 – Faktor zur Berücksichtigung des Betonzustands; k9 = 1,7 für gerissenen Beton, k9 = 2,4 für ungerissenen Beton
- \( \alpha = 0,1 \left ( \frac{l_f}{c_1} \right ) ^{0.5} \)
- \( \beta = 0,1 \left ( \frac{d_{nom}}{c_1} \right ) ^{0.2} \)
- lf = min (hef, 12 dnom) for dnom ≤ 24 mm; lf = min [hef, max (8 dnom, 300 mm)] für dnom > 24 mm – Wirksame Länge des auf Schub belasteten Ankers
- hef – Einbettungstiefe des Ankers in Beton
- c1 – Abstand vom Anker zur untersuchten Kante; für Anker in einem schmalen dünnen Träger wird der wirksame Abstand \( c'_1=\max \left \{ \frac{c_{2,max}}{1,5}, \, \frac{h}{1,5}, \, \frac{s_{2,max}}{3} \right \} \) verwendet
- c2 – Kleinerer Abstand zur Betonkante senkrecht zum Abstand c1
- dnom – Nomineller Ankerdurchmesser
- Ac,V0 = 4,5 c12 – Fläche des des Betonkegels eines einzelnen Ankers an der seitlichen nicht von Kanten betroffenen Betonfläche
- Ac,V – Tatsächliche Fläche des Betonkegels der Verankerung an der seitlichen Betonoberfläche
- \(\psi_{s,V} = 0,7+0,3 \frac{c_2}{1.5 c_1} \le 1,0 \) – Faktor zur Berücksichtigung der Störung der Spannungsverteilung im Beton durch weitere Kanten des Betonbauteils auf die Schubtragfähigkeit
- \( \psi_{h,V} = \left ( \frac{1,5 c_1}{h} \right ) ^ {0,5} \ge 1,0 \) – Faktor, der berücksichtigt, dass die Schubtragfähigkeit nicht proportional zur Bauteildicke abnimmt, wie im Verhältnis Ac,V / Ac,V0 angenommen
- \( \psi_{ec,V} = \frac{1}{1+2 e_V / (3c_1)} \le 1 \) – Faktor zur Berücksichtigung der Gruppenwirkung, wenn unterschiedliche Querlasten auf die einzelnen Anker einer Gruppe wirken
- \( \psi_{\alpha,V} = \sqrt{\frac{1}{(\cos \alpha_V)^2 + (0,5 \sin \alpha_V)^2}} \ge 1 \) – Zur Berücksichtigung des Winkels αV zwischen der aufgebrachten Last V und der Lastrichtung senkrecht zur freien Kante des Betonbauteils
- ψre,V = 1,0 – Faktor zur Berücksichtigung des Einflusses der Bewehrungsart in gerissenem Beton
- h – Höhe des Betonblocks
- γMc = γc – Teilsicherheitsfaktor (EN 1992-4 – Tabelle 4.1, γinst = 1,0 für Scherlasten)
- γc – Teilsicherheitsfaktor für Beton (änderbar in den Normeinstellungen)
Interaktion von Zug und Schub im Stahl
Die Interaktion von Zug und Schub wird für Stahl- und Betonversagen getrennt nach Tabelle 7.3 bestimmt. Die Interaktion im Stahl wird nach Gleichung (7.54) nachgewiesen. Die Interaktion im Stahl wird separat geprüft.
\[ \left ( \frac{N_{Ed}}{N_{Rd,s}} \right )^2 + \left ( \frac{V_{Ed}}{V_{Rd,s}} \right )^2 \le 1,0 \]
Interaktion von Zug und Schub im Beton
Die Interaktion im Beton wird gemäß Gleichung (7.55) nachgewiesen.
\[ \left ( \frac{N_{Ed}}{N_{Rd,i}} \right )^{1,5} + \left ( \frac{V_{Ed}}{V_{Rd,i}} \right )^{1,5} \le 1,0 \]
Es wird der kleinere der Werte \(N_{Ed} / N_{Rd,i} \) und \(V_{Ed} / V_{Rd,i} \) für verschiedene Versagensarten verwendet. Beachten Sie, dass die Werte für \(N_{Ed}\) und \(N_{Rd,i}\) oft zu einer Ankergruppe gehören.
Abstandsanker
Abstandshalter werden als Stabelement ausgeführt, die durch Querkräfte, Biegemoment und Druck- oder Zugkraft belastet werden. Diese Schnittgrößen werden durch das Finite-Elemente-Modell ermittelt. Der Anker wird beidseitig befestigt, eine Seite liegt 0,5×d unterhalb der Betonebene, die andere Seite liegt in der Mitte der Plattendicke. Die Knicklänge wird konservativ mit der doppelten Länge des Stabelements angenommen. Es wird ein plastischer Widerstandsmodul verwendet. Die Bemessung des Stabelements erfolgt nach EN 1993-1-1. Die Scherkraft kann die Streckgrenze des Stahls gemäß Abs. 6.2.8 verringern aber die Mindestlänge des Ankers, um die Mutter unter der Fußplatte zu montieren, stellt sicher, dass der Anker beim Biegen versagt, bevor die Scherkraft die Hälfte der Scherkrafttragfähigkeit erreicht. Die Reduzierung ist daher nicht erforderlich. Die Interaktion von Biegemoment und Druck- bzw. Zugfestigkeit wird nach Abs. 6.2.1 bewertet.
Schertragfähigkeit (EN 1993-1-1 Abs. 6.2.6):
\[ V_{pl,Rd} = \frac{A_V f_y / \sqrt{3}}{\gamma_{M2}} \]
Wo:
- AV = 0,844 As – Scherfläche
- As – Durch Gewinde reduzierte Schraubenfläche
- fy – Streckgrenze der Schraube
- γM2 – Teilsicherheitsfaktor
Zugtragfähigkeit (EN 1993-1-8 – Abs. 3.6.1):
\[ F_{t,Rd}=\frac{c k_2 f_{ub} A_s}{\gamma_{M2}} \ge F_t \]
Wo:
- c – Abnahme der Zugtragfähigkeit von Schrauben mit geschnittenem Gewinde nach EN 1993-1-8 – Abs. 3.6.1. (3); änderbar in den Normeinstellungen
- k2 = 0,9 – Faktor aus Tabelle 3.4 in EN 1993-1-8
- fub – Zugfestigkeit des Ankerbolzens
- As – Zugspannungsfläche der Ankerschraube
- γM2 – Sicherheitsfaktor (EN 1993-1-8 – Table 2.1; änderbar in den Normeinstellungen)
Drucktragfähigkeit (EN 1993-1-1 Abs. 6.3):
\[ F_{c,Rd} = \frac{\chi A_s f_y}{\gamma_{M2}} \]
Wo:
- \( \chi = \frac{1}{\Phi + \sqrt{\Phi^2 - \bar\lambda^2}} \le 1 \) – Knickreduktionsfaktor
- \( \Phi = 0,5 \left [1+ \alpha (\bar\lambda - 0.2) + \bar\lambda^2 \right ] \) – Wert zur Ermittlung des Knickreduktionsfaktors χ
- α = 0,49 – Imperfektionsbeiwert für Knickkurve c (zum Vollkreis gehörend)
- \( \bar\lambda = \sqrt{\frac{A_s f_y}{N_{cr}}} \) – Relative Schlankheit
- \( N_{cr} = \frac{\pi^2 E I}{L_{cr}^2} \) – Kritische Eulerkraft
- \( I = \frac{\pi d_s^4}{64} \) – Trägheitsmoment der Schraube
- Lcr = 2 l – Knicklänge; sicherheitshalber wird davon ausgegangen, dass die Schraube im Beton fixiert ist und sich an der Fußplatte frei drehen kann
- l – Länge des Schraubenelements gleich halber Fußplattendicke + Spalt + halber Schraubendurchmesser; es wird sicherheitshalber davon ausgegangen, dass die Unterlegscheibe und die Mutter nicht an der Betonoberfläche festgeklemmt sind (ETAG 001 – Anhang C – Abs. 4.2.2.4)
Biegetragfähigkeit (EN 1993-1-1 Abs. 6.2.5):
\[ M_{pl,Rd} = \frac{W_{pl} f_y}{\gamma_{M2}} \]
- \( W_{pl}= \frac{d_s^3}{6} \) – Widerstandsmoment der Schraube
- fy – Streckgrenze der Schraube
- γM2 – Teilsicherheitsfaktor
Ausnutzung des Ankerstahl (EN 1993-1-1 Abs. 6.2.1)
\[ \frac{N_{Ed}}{N_{Rd}} + \frac{M_{Ed}}{M_{Rd}} \le 1 \]
Wo:
- NEd – Bemessungswert der Zug-(+) oder Druck-(-)kraft
- NRd – Bemessungswert der Zug- (+, Ft,Rd) oder Druck-(-, Fc,Rd)tragfähigkeit
- MEd – Bemessungswert des Biegemoments
- MRd = Mpl,Rd – Bemessungswert der Biegetragfähigkeit
Nachweis des Betonblocks nach Eurocode
Beton unterhalb der Fußplatte wird vom Winkler-Untergrund mit gleichmäßiger Steifigkeit simuliert, die die Kontaktspannungen liefert. Für den Drucknachweis wird die nach EN 1993-1-8 ermittelte mittlere Spannung an der wirksamen Fläche verwendet.
Die Tragfähigkeit von Beton bei räumlichem Druck wird in Anlehnung an EN 1993-1-8 durch Berechnung der Bemessungstragfähigkeit des Betons im Anschluss fjd unter der wirksamen Fläche Aeff der Fußplatte ermittelt. Die Bemessungstragfähigkeit des Anschlusses fjd wird nach Abs. 6.2.5 in EN 1993-1-8 und Abs. 6.7 in EN 1992-1-1 ermittelt. Die Qualität und Dicke des Mörtels wird durch den Fugenbeiwert βjd bestimmt. Für eine Mörtelqualität gleich oder besser als die Qualität des Betonblocks wird βjd = 1,0 angenommen, EN 1993-1-8 empfiehlt den Wert βjd = 0,67. Die wirksame Fläche Aeff,cm unter der Fußplatte wird als die Form des Stützenquerschnitts, vergrößert um zusätzliche Ausbreitungsbreite c, ermittelt.
\[ c = t \sqrt{\frac{f_y}{3 f_{jd} \gamma_{M0}}} \]
mit t als Dicke der Fußplatte, fy der Streckgrenze der Fußplatte und γM0 als Teilsicherheitsbeiwert für Stahl.
Die wirksame Fläche wird durch Iteration berechnet, bis die Differenz zwischen den zusätzlichen Ausbreitungsbreiten der aktuellen und vorherigen Iteration |ci – ci–1 | weniger als 1 mm beträgt. Für die erste Iteration wird die Fläche der Fußplatte als tragende Fläche Ac0 angenommen.
Die Fläche, in der der Beton unter Druck steht, wird den Ergebnissen der FEM entnommen. Diese aus Druck belastete Fläche Aeff,FEM ermöglicht das Ermitteln der Position der neutralen Achse. Der Nutzer kann diese Fläche ändern, indem er in den Normeinstellungen „Wirksamer Bereich – Einfluss der Netzgröße“ bearbeitet. Der Standardwert ist 0,1, für den die Verifizierungsstudien durchgeführt wurden. Es wird nicht empfohlen, diesen Wert zu verringern. Eine Erhöhung dieses Wertes macht die Beurteilung der Betontragfähigkeit sicherer. Der Wert in den Normeinstellungen bestimmt die Grenze des Bereichs, Aeff,FEM, z.B. berücksichtigt der Wert von 0,1 nur Bereiche, in denen die Betonspannung größer ist als das 0,1-fache der maximalen Betonspannung, σc,max. Der Schnittpunkt der Druckfläche Aeff,FEM und der wirksamen Fläche Aeff,cm ermöglicht die Bewertung der Tragfähigkeit für eine allgemein belastete Fußplatten jeder Form mit beliebigen Versteifungen und wird mit Aeff bezeichnet. Die durchschnittliche Spannung σ auf der wirksamen Fläche, Aeff, wird als Druckkraft dividiert durch die wirksame Fläche bestimmt. Nachweis des Bauteils auf Spannungen mit σ ≤ fjd.
Betontragfähigkeit bei konzentriertem Druck:
\[ f_{jd}= \beta_j k_j \frac{f_{ck}}{\gamma_c} \]
Konzentrationsfaktor unter Berücksichtigung der Erhöhung der Betondruckfestigkeit durch mehraxiale Spannung:
\[ k_j=\sqrt{\frac{A_{c1}}{A_{eff}}} \le 3,0 \]
mit Ac1 nach EN 1992-1-1 – Abs. 6.7. Die Fläche muss konzentrisch und geometrisch ähnlich der tragenden Fläche Aeff sein.
Durchschnittliche Spannung unter der Fußplatte:
\[ \sigma = \frac{N}{A_{eff}} \]
Ausnutzung bei Druck [%]:
\[ Ut = \frac{\sigma}{f_{jd}} \]
Wo:
- fck – Charakteristische Druckbetonfestigkeit
- βj = 0,67 – Faktor der Mörtelqualität, änderbar in den Normeinstellungen
- γc – Sicherheitsfaktor für Beton
- Aeff – Wirksame Fläche, auf die sich die Normalkraft N verteilt
Die wirksame Fläche, Aeff,cm, berechnet nach EN für reinen Druck, ist mit einer gestrichelten Linie markiert. Die grafische Darstellung zeigt die Art der Überprüfung. Die berechnete wirksame Fläche Aeff,fem ist grün markiert. Die endgültige wirksame Fläche, Aeff, für den Nachweis der Kontaktspannung ist schraffiert hervorgehoben.
In seltenen Fällen, insbesondere bei nur durch Zugkraft belasteten Fußplatten (Druck im Beton wird durch Abstützkräfte verursacht) oder Zugkraft und Biegemoment, ist der Schnittpunkt der Flächen Aeff,cm und Aeff,fem sehr klein oder gar nicht vorhanden. In solchen Fällen sind die Druckkräfte im Allgemeinen sehr klein, der Nachweis liegt außerhalb des Geltungsbereichs des Eurocodes und der Beton unter Druck wird nicht nachgewiesen.
Netzsensitivität
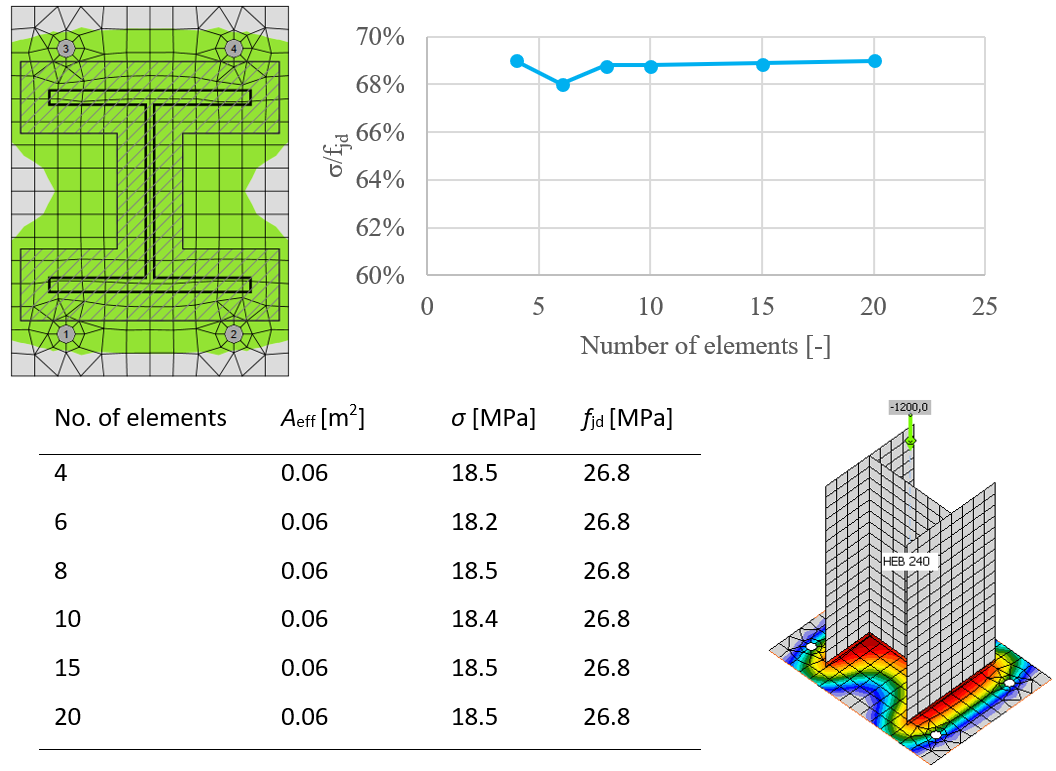
Dieses Verfahren zur Beurteilung der Druckfestigkeit des Betons ist unabhängig vom Netz der Fußplatte, wie in den folgenden Abbildungen zu sehen ist. Sie wird am Beispiel von Beton in der Druckbemessung nach EN gezeigt. Es wurden zwei Fälle untersucht: Belastung durch reinen Druck von 1200 kN und Belastung durch eine Kombination von Druckkraft 1200 kN und Biegemoment 90 kN.
Einfluss der Anzahl der Elemente auf die Vorhersage des Drucktragfähigkeit des Betons bei reinem Druck
Der Einfluss der Anzahl der Elemente auf die Vorhersage die Tragfähigkeit des Betons unter Druck bei Druck und Biegung
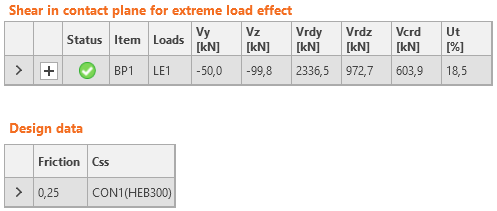
Schub im Betonblock
Schub in Betonblock kann auf eine der drei Arten übertragen werden:
- Reibung
\( Ut = \frac{V}{V_{Rd}} \)
Vrd = N * Cf
- Scherlasche
\( Ut = \max \left ( \frac{V_y}{V_{Rd,y}}, \, \frac{V_z}{V_{Rd,z}}, \, \frac{V}{V_{c,Rd}} \right ) \) \(V_{Rd,y} = \frac{A_{Vy} f_y}{\sqrt{3} \gamma_{M0}} \)
\( V_{Rd,z} = \frac{A_{Vz} f_y}{\sqrt{3} \gamma_{M0}} \)
\( V_{c,Rd} = A \sigma_{Rd,max} \)
Profildübel und Schweißnähte werden ebenfalls durch die FEM überprüft.
- Anker
Der Nachweis erfolgt gemäß ETAG 001 - Anhang C
Wo:
- AV,y, AV,z – Scherflächen des Querschnitts der Scherlasche in Richtung der Achsen y und z
- fy – Streckgrenze
- γM0 – Sicherheitsfaktor
- Vy – Scherkraftkomponente in der Ebene der Fußplatte in y-Achsrichtung
- Vz – Scherkraftkomponente in der Ebene der Fußplatte in z-Achsrichtung
- V – Scherkraft (Vektorsumme beider Scherkraftkomponenten)
- N – Kraft senkrecht zur Fußplatte
- Cf – Reibungskoeffizient zwischen Stahl und Beton/Mörtel; änderbar in den Normeinstellungen
- A = l * b – Projizierte Fläche der Scherlasche ohne den Bereich über der Betonoberfläche
- l – Länge der Scherlasche ohne den Bereich über der Betonoberfläche
- b – Projizierte Breite der Scherlasche in Richtung der Schubbelastung
- σRd,max = k1 * v' * fcd – Maximale Spannung, die an den Kanten des Knotens aufgebracht werden kann
- k1 = 1 – Faktor (EN 1992-1-1 – Gleichung (6.60))
- v' = 1 – fck / 250 – Faktor (EN 1992-1-1 – Gleichung (6.57N))
- \( f_{cd} = \alpha_{cc} \frac{f_{ck}} {\gamma_c} \) – Bemessungsdruckfestigkeit des Betons
- αcc – Koeffizient für Langzeitwirkungen auf die Druckfestigkeit von Beton
- fck – Charakteristische Druckfestigkeit des Betons
- γc – Sicherheitsfaktor für Beton
Kapazitätsbemessung nach Eurocode
Die Kapazitätsbemessung ist Teil eines Erdbebennachweises und stellt sicher, dass der Anschluss eine ausreichende Verformungskapazität aufweist.
Das Ziel der Kapazitätsbemessung besteht darin, zu bestätigen, dass ein Gebäude ein kontrolliertes duktiles Verhalten aufweist, um einen Einsturz bei einem Erdbeben auf Konstruktionsebene zu vermeiden. Es wird erwartet, dass ein plastisches Gelenk in einem dissipativen Element auftreten, und alle nicht-dissipativen Elemente des Gelenks müssen in der Lage sein, Kräfte aufgrund des Nachgebens in dem dissipativen Element sicher zu übertragen. Das dissipative Element ist normalerweise ein momenttragfähiger Rahmen, kann aber auch z.B. eine Stirnplatte sein. Der Sicherheitsfaktor wird für dissipative Elemente nicht verwendet. Dem dissipativen Element werden zwei Faktoren zugeordnet:
- γov – Überfestigkeitsfaktor – EN 1998-1, Abs. 6.2
- Empfohlener Wert ist γov = 1,25; änderbar in den Materialien - γsh – Wiederverfestigungsfaktor – EN 1998-1
- Empfohlene Werte sind γsh = 1,2 für Bauteile in momenttragfähigen Rahmen, ansonsten γsh = 1,0; änderbar in der Operation
Das Materialdiagramm wird gemäß der folgenden Abbildung modifiziert:
Die erhöhte Festigkeit des dissipativen Elements (fy,max = fy ⋅ γov ⋅ γsh) ermöglicht die Eingabe von Lasten (My,Ed, Vz,Ed), die dazu führen, dass ein plastische Gelenk in dem dissipativen Element auftritt. Im Fall eines momenttragenden Rahmens und Bauteils als dissipatives Element sollte das Bauteil mit My,Ed = γov ⋅ γsh ⋅ fy ⋅ Wpl,y und der entsprechenden Querkraft Vz,Ed = –2 ⋅ My,Ed / Lh belastet werden, mit:
- fy – Charakteristische Streckgrenze
- Wpl,y – Plastischer Widerstandsmodul
- Lh – Abstand zwischen plastischen Gelenken am Bauteil
Bei einem asymmetrischen Anschluss sollte das Bauteil sowohl durch durchhängende als auch durch ziehende Biegemomente und die entsprechenden Querkräfte belastet werden.
Die Platten von dissipativen Elementen sind vom Nachweis ausgeschlossen.
Beulanalyse nach Eurocode
Die Belastungstragfähigkeit schlanker Komponenten kann durch eine Kombination aus linearer Beulanalyse und materiell nichtlinearer Analyse bestimmt werden.
Es gibt fünf Kategorien der Finite-Elemente-Strukturanalyse mit folgenden Annahmen:
- Lineares Material, geometrisch linear
- Nichtlineares Material, geometrisch linear
- Lineares Material, linearer Stabilitätsverlust – Beulen
- Lineares Material, geometrisch nichtlinear mit Imperfektionen
- Nichtlineares Material, geometrisch nichtlinear mit Imperfektionen
Ein Bemessungsverfahren, das die Ansätze 2 und 3 kombiniert - Material-Nichtlinearitäts- und Stabilitätsanalyse - wird in Kapitel 8 der EN 1993-1-6 genannt. Die Überprüfung der Beulfestigkeit auf der Grundlage der erhaltenen FEM-Ergebnisse ist in Anhang B der EN 1993-1-5 beschrieben. Dieses Verfahren wird für eine Vielzahl von Strukturen verwendet, mit Ausnahme von sehr schlanken Schalen, bei denen eine geometrisch nichtlineare Analyse mit anfänglichen Imperfektionen besser geeignet ist (4 und 5).
Das Verfahren verwendet Lastverstärker α, die als Ergebnisse der FEM-Analyse erhalten werden und die Vorhersage der Nachbeulfestigkeit der Anschlüsse ermöglichen.
Der Lastkoeffizient αult,k wird durch Erreichen der plastischen Kapazität, ohne Berücksichtigung der geometrischen Nichtlinearität, bestimmt. Die Überprüfung der plastischen Kapazität und die allgemeine automatische Bestimmung von αult,k ist in der Software implementiert.
Es wird der kritische Beulkfaktor αcr ermittelt, der unter Verwendung einer FEM-Analyse der linearen Stabilität erhalten wird. Sie wird in der Software automatisch unter Verwendung des gleichen FEM-Modells wie für die Berechnung von αult,k ermittelt. Es ist zu beachten, dass der kritische Punkt, in Bezug auf den plastischen Widerstand, nicht unbedingt im ersten kritischen Beulmodus bewertet wird. In einem komplexen Anschluss müssen mehr Beulmodi bewertet werden, da sie sich auf verschiedene Teile des Anschlusses beziehen.
Die dimensionslose Plattenschlankheit \(\bar{\lambda_p} \) des untersuchten Beulmodus wird ermittelt durch:
\[ \bar \lambda_p = \sqrt{\frac{\alpha_{ult,k}}{\alpha_{cr}}} \]
Der Beulreduktionsfaktor ρ wird gemäß Anhang B der EN 1993-1-5 ermittelt. Der Reduktionsfaktor hängt von der Plattenschlankheit ab. Die verwendete Beulkurve zeigt den Einfluss des Reduktionsfaktors auf die Plattenschlankheit. Der für ungleichmäßige Bauteile geltende Beulfaktor basiert auf den Beulkurven eines Trägers. Die Verifizierung basiert auf dem von Mises-Fließkriterium und der Methode der reduzierten Spannung. Der Beulwiderstand wird bewertet als
\[ \frac{\alpha_{ult,k} \rho}{\gamma_{M2}} \ge 1 \]
Beulreduktionsfaktor ρ gemäß EN 1993-1-5 Anhang B.
Obwohl der Prozess trivial erscheint, ist er allgemein, stabil und leicht zu automatisieren. Der Vorteil des Verfahrens ist die erweiterte FEM-Analyse der gesamten Verbindung, die auf die allgemeine Geometrie angewendet werden kann. Darüber hinaus ist es in den gültigen Eurocode-Standards enthalten. Die erweiterte numerische Analyse gibt einen schnellen Überblick über das globale Verhalten der Struktur und ihrer kritischen Teile und ermöglicht eine schnelle Versteifung, um Instabilitäten zu vermeiden.
Die Grenzschlankheit λp ist in Anhang B der EN 1993-1-5 angegeben und legt alle Fälle fest, die nach dem vorherigen Verfahren bewertet werden müssen. Der Widerstand wird durch Beulen für eine Plattenschlankheit von mehr als 0,7 begrenzt. Mit abnehmender Schlankheit wird der Widerstand durch plastische Beanspruchung bestimmt. Der kritische Grenzbeulfaktor für die Plattenschlankheit beträgt 0,7, und der Beulwiderstand (entspricht dem plastischen Widerstand) kann wie folgt erhalten werden
\[ \alpha_{cr} = \frac{\alpha_{ult,k}}{\bar \lambda_p^2} = \frac{1}{0.7^2} = 2.04 \]
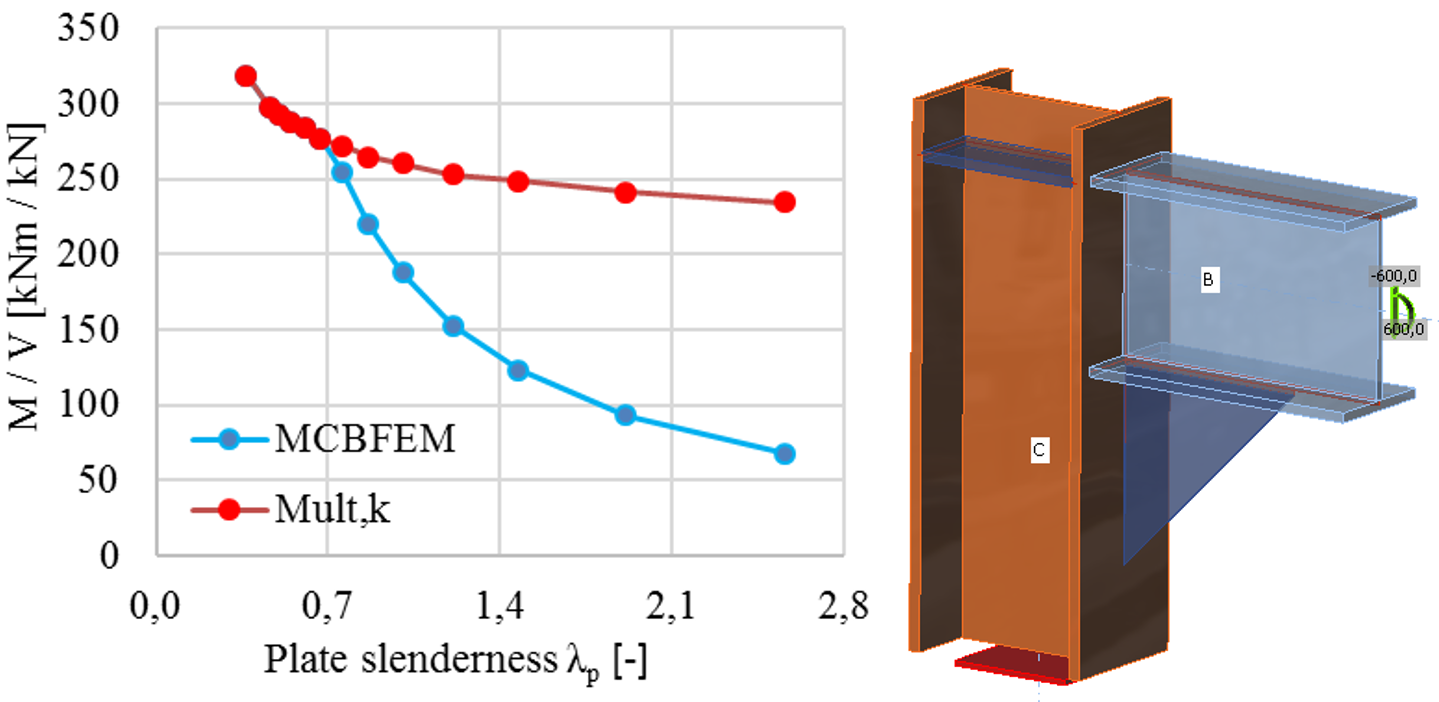
Der Einfluss der Plattenschlankheit auf den plastischen Widerstand Mult,k und den Knickwiderstand MCBFEM ist in der folgenden Abbildung dargestellt. Das Diagramm zeigt die Ergebnisse einer numerischen Untersuchung einer dreieckigen Steife in einer Portalrahmenverbindung.
Der Einfluss der Plattenschlankheit auf den Widerstand der Portalrahmenverbindung mit schlanker Steife
Anschlussklassifizierung (EN)
Anschlüsse werden nach Anschlusssteifigkeit klassifiziert in:
- Starr – Anschlüsse mit unbedeutender Änderung der ursprünglichen Winkel zwischen den Bauteilen,
- Halbstarr – Anschlüsse, von denen angenommen wird, dass sie in der Lage sind, ein zuverlässiges und bekanntes Maß an Biegesteifigkeit zu erbringen,
- Gelenkig – Anschlüsse, die keine Biegemomente entwickeln.
Anschlüsse werden EN 1993-1-8 – Abs. 5.2.2 klassifiziert in
- Starr – \( \frac{S_{j,ini} L_b}{E I_b} \ge k_b \)
- Halbstarr – \( 0.5 < \frac{S_{j,ini} L_b}{E I_b} < k_b \)
- Gelenkig – \( \frac{S_{j,ini} L_b}{E I_b} \le 0.5 \)
mit:
- Sj,ini – anfängliche Steifigkeit des Anschlusses; die Anschlusssteifigkeit wird bis auf 2/3 von Mj,Rd als linear angenommen
- Lb – Theoretische Länge des analysierten Bauteils; eingestellt in den Bauteileigenschaften
- E – Elastizitätsmodul
- Ib – Trägheitsmoment des analysierten Bauteils
- kb = 8 für Rahmen, bei denen das Aussteifungssystem die horizontale Verschiebung um mindestens 80 % reduziert; kb = 25 für andere Rahmen, sofern in jeder Etage Kb/Kc ≥ 0,1. Der Wert kb = 25 wird verwendet, es sei denn, der Nutzer stellt in den Normeinstellungen "ausgesteiftes System" ein.
- Mj,Rd – Momententragfähigkeit des Anschlusses
- Kb = Ib / Lb
- Kc = Ic / Lc
Horizontale Zugverankerung
Verbindungen müssen so ausgelegt sein, dass sie Zugkräfte umwandeln, die durch Effekte zweiter Ordnung erzeugt werden – Stütze wird entfernt und der Boden wirkt als Membran.
Auflager
Es wird nur ein Bauteil analysiert und alle anderen Bauteile werden an ihren Enden fixiert. Auf das analysierte Bauteil sollte nur die Normalkraft aufgebracht werden, daher wird sein Modelltyp auf N-Vy-Vz eingestellt (Biegemomente und Torsion sind eingeschränkt).
Belastung
Die auf das analysierte Bauteil wirkende Normalkraft sollte gemäß EN 1993-1-7, Abs. A.5.1:
Für innere Bindungen:
\[T_i=0.8(g_k+\psi q_k) s L \ge 75 \textrm{ kN} \]
Für Randbindungen:
\[T_p=0.4(g_k+\psi q_k) s L \ge 75 \textrm{ kN} \]
Wo:
- \(g_k\) – Charakteristische ständige Last
- \(q_k\) – Charakteristische auferlegte Last
- \(s\) – Abstand der Bindungen
- \(L\) – Spannweite der Bindung
- \(\psi\) – relevanter Faktor im Ausdruck für eine Kombination von Schnittgrößen für die zufällige Bemessungssituation (z.B. \(\psi_1\) oder \(\psi_2\) gemäß Ausdruck (6.11b) in EN 1990).
Materialmodell und Nachweis
Gemäß SCI P358: Joints in steel construction: Simple Joints to Eurocode 3 – Anhang A, wird der Teilsicherheitsbeiwert für horizontale Zugverankerung eingeführt, \(\gamma_{Mu}\) mit Standardwert 1,1 änderbar in den Normeinstellungen. Dieser Sicherheitsfaktor wird für Bleche, Schrauben und Schweißnähte in der Analyse der horizontalen Zugverankerung verwendet.
Es werden extreme Belastungen und Verformungen erwartet und die Bemessung der Platten basiert auf der Höchstfestigkeit der Platten, \(f_u\). Deshalb verhält sich das Materialmodell für die Finite-Elemente-Analyse elastisch bis zu \(f_u / \gamma_{Mu}\). Die Steigung des plastischen Zweigs ist der Elastizitätsmodul von Young \(E/1000\). Es wird ein Nachweis auf eine plastische Dehnungsgrenze von 5% durchgeführt.
Die Widerstände von Schrauben und Schweißnähten werden mit \(\gamma_{Mu}\) anstelle von \(\gamma_{M2}\) berechnet. Bei Verwendung der Standardwerte der Teilsicherheitsbeiwerte liegen die Lastwiderstände um etwa 14% höher als im Grenzzustand der Tragfähigkeit.
Bei vorgespannten Schrauben wird davon ausgegangen, dass sie gleiten, und sie werden als normale, festsitzende Schrauben geprüft.
Referenzen
EN 1993-1-7: Eurocode 1 – Actions on structures – Part 1-7: General actions – Accidental actions, CEN, 2006
SCI P358: Joints in steel construction: Simple Joints to Eurocode 3