Base théorique

Code-check of anchors (AISC)

Steel

Connection

AISC (USA)

Anchoring

CBFEM

Concrete block

Steel-to-concrete

Cet article est aussi disponible en :

The forces in anchors including prying forces are determined by finite element analysis, but the resistances are checked using code provisions of ACI 318-14 - Chapter 17.

Only LFRD is available. Anchor rods are designed according to AISC 360-16 – J9 and ACI 318-14 – Chapter 17. The following resistances of anchor bolts are evaluated:

Steel strength of anchor in tension ϕN_sa,
Concrete breakout strength in tension ϕN_cbg,
Concrete pullout strength ϕN_p,
Concrete side-face blowout strength ϕN_sb,
Steel strength of anchor in shear ϕV_sa,
Concrete breakout strength in shear ϕV_cbg,
Concrete pryout strength of anchor in shear ϕV_cp.

The user must choose the concrete condition (cracked or non-cracked – with no cracks in service condition) and the type of anchors (with or without washer plates).

Following checks of anchors loaded in tension are not provided and should be checked using information in relevant Technical Product Specification (based on the 5 percent fractile of tests performed and evaluated according to ACI 355.2):

Pull-out failure of fastener (for post-installed mechanical anchors) – ACI 318-19: 17.6.3,
Bond strength of adhesive anchor (for post-installed bonded anchors) – ACI 318-19: 17.6.5,
Concrete splitting failure during installation should be evaluated by ACI 355.2 requirements.

Concrete blow-out failure is provided only for anchors with washer plates.

Steel strength of anchor in tension

Steel strength of anchor in tension is determined according to ACI 318-14 – 17.4.1 as

ϕN_sa = ϕ A_se,N f_uta

where:

ϕ = 0.7 – strength reduction factor for anchors in tension according to ACI 318-14 – 17.3.3, the factor is editable in Code setup
A_se,N – tensile stress area
f_uta – specified tensile strength of anchor steel and shall not be greater than 1.9 f_ya and 125 ksi

Concrete breakout strength

Concrete breakout strength is designed according to the Concrete Capacity Design (CCD) in ACI 318-14 – Chapter 17. In the CCD method, the concrete cone is considered to be formed at an angle of approximately 34° (1 vertical to 1.5 horizontal slope). For simplification, the cone is considered to be square rather than round in plan. The concrete breakout stress in the CCD method is considered to decrease with an increase in size of the breakout surface. Consequently, the increase in strength of the breakout in the CCD method is proportional to the embedment depth to the power of 1.5. Anchors whose concrete cones overlap create a group of anchors which create a common concrete cone. Note that no equivalent ASD solution exists for concrete capacity design.

\[ \phi N_{cbg} = \phi \frac{A_{Nc}}{A_{Nco}} \psi_{ec,N} \psi_{ed,N} \psi_{c,N} \psi_{cp,N} N_b \]

where:

ϕ = 0.7 – strength reduction factor for anchors in tension according to ACI 318-14 – 17.3.3, the factor is editable in Code setup
A_Nc – actual concrete breakout cone area for a group of anchors that create a common concrete cone
A_Nco = 9 h_ef² – concrete breakout cone area for single anchor not influenced by edges
\( \psi_{ec,N} = \frac{1}{1+\frac{2 e'_N}{3 h_{ef}}} \) – modification factor for anchor groups loaded eccentrically in tension; in the case where eccentric loading exists about two axes, the modification factor Ψ_ec,N is calculated for each axis individually and the product of these factors is used
\( \psi_{ed,N} = \min \left ( 0.7 + \frac{0.3 c_{a,min}}{1.5 h_{ef}}, 1 \right ) \) – modification factor for edge distance
c_a,min – smallest distance from the anchor to the edge
Ψ_c,N – modification factor for concrete conditions; Ψ_c,N =1 for cracked concrete, Ψ_c,N =1.25 for non-cracked concrete
Ψ_cp,N = min (c_a,min / c_ac,1) – modification factor for splitting for post-installed anchors designed for uncracked concrete without supplementary reinforcement to control splitting; Ψ_cp,N = 1 for all other cases
\( N_b = k_c \lambda_a \sqrt{f'_c} h_{ef}^{1.5} \) – basic concrete breakout strength of a single anchor in tension in cracked concrete; for cast-in anchors and 11 in. ≤ h_ef ≤ 25 in. \( N_b = 16 \lambda_a \sqrt{f'_c} h_{ef}^{5/3} \)
k_c = 24 for cast-in anchors
h_ef – depth of embedment; according to Chapter 17.4.2.3 in ACI 318-14, the effective embedment depth h_ef is reduced to \( h_{ef} = \max \left ( \frac{c_{a,max}}{1.5}, \frac{s}{3} \right ) \) if anchors are located less than 1.5 h_ef from three or more edges
s – spacing between anchors
c_a,max – maximum distance from an anchor to one of the three close edges
λ_a = 1 – modification factor for lightweight concrete
f'_c – concrete compressive strength [psi]

According to ACI 318-14 – 17.4.2.8, in case of headed anchors, the projected surface area A_Nc is determined from the effective perimeter of the washer plate, which is the lesser value of d_a + 2 t_wp or d_wp, where:

d_a – anchor diameter
d_wp – washer plate diameter or edge size
t_wp – washer plate thickness

The group of anchors is checked against the sum of tensile forces in anchors loaded in tension and creating a common concrete cone.

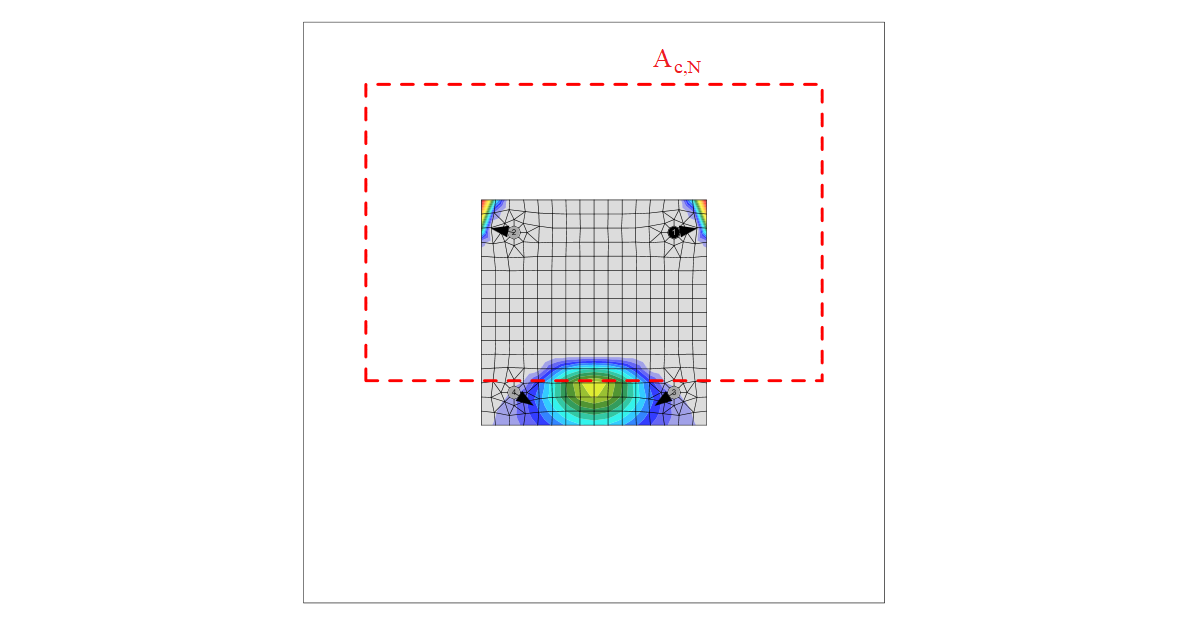
The concrete breakout cone area for group of anchors loaded by tension that create common concrete cone, A_c,N, is shown by red dashed line.

According to ACI 318-14 – 17.4.2.9, where anchor reinforcement is developed in accordance with ACI 318-14 – 25 on both sides of the breakout surface, the anchor reinforcement is presumed to transfer the tension forces, and concrete breakout strength is not evaluated.

Concrete pullout strength

Anchor bolts with washer plate (headed bolts):

Concrete pullout strength of a headed anchor bolt is defined in ACI 318-14 – 17.4.3 as

ϕN_pn = ϕΨ_c,P N_p

where:

ϕ = 0.7 – strength reduction factor for anchors in tension according to ACI 318-14 – 17.3.3, editable in Code setup
Ψ_c,P – modification factor for concrete condition; Ψ_c,P = 1.0 for cracked concrete, Ψ_c,P = 1.4 for non-cracked concrete
N_P = 8 A_brg f'_c for headed anchor
A_brg – bearing area of the head of stud or anchor bolt
f'_c – concrete compressive strength

Hooked anchor bolts (J- or L-bolts):

Concrete pullout strength of a hooked anchor bolt is defined in ACI 318-14 – 17.4.3 as

ϕN_pn = ϕΨ_c,P N_p

where:

ϕ = 0.7 – strength reduction factor for anchors in tension according to ACI 318-14 – 17.3.3, editable in Code setup
Ψ_c,P – modification factor for concrete condition; Ψ_c,P = 1.0 for cracked concrete, Ψ_c,P = 1.4 for non-cracked concrete
N_P = 0.9 f'_c e_h d_a for hooked anchor bolt
f'_c – concrete compressive strength
e_h – distance from the inner surface of the shaft of a J- or L-bolt to the outer tip of the J- or L-bolt
d_a – anchor bolt diameter

Concrete pullout strength for other types of anchors than headed or hooked is not evaluated in the software and has to be specified by the manufacturer.

Concrete side-face blowout strength

Concrete side-face blowout strength of headed anchor in tension is defined in ACI 318-14 – 17.4.4 as

\[ \phi N_{sb} = \phi 160 c_{a1} \sqrt{A_{brg}} \sqrt{f'_c} \]

The concrete side-face blowout strength is multiplied by one of reduction factors:

\( \frac{1+\frac{c_{a2}}{c_{a1}}}{4} \le 1 \)
\( \frac{1+\frac{s}{6 c_{a1}}}{2} \le 1 \)

where:

ϕ = 0.7 – strength reduction factor for anchors in tension according to ACI 318-14 – 17.3.3, editable in Code setup
c_a1 – shorter distance from the centreline of an anchor to an edge
c_a2 – longer distance, perpendicular to c_a1, from the centreline of an anchor to an edge
A_brg – bearing area of the head of stud or anchor bolt
f'_c – concrete compressive strength
s – spacing between two adjacent anchors near one edge

Steel strength in shear

The steel strength in shear is determined according to ACI 318-14 – 17.5.1 as

ϕV_sa = ϕ 0.6 A_se,V f_uta

where:

ϕ = 0.65 – strength reduction factor for anchors in tension according to ACI 318-14 – 17.3.3, editable in Code setup
A_se,V – tensile stress area
f_uta – specified tensile strength of anchor steel and shall not be greater than 1.9 f_ya and 125 ksi

If mortar joint is selected, steel strength in shear V_sa is multiplied by 0.8 (ACI 318-14 – 17.5.1.3).

The shear on lever arm, which is present in the case of base plate with oversized holes and washers or plates added to the top of the base plate to transmit the shear force, is not considered.

Concrete breakout strength of anchor in shear

The concrete breakout strength of an anchor or anchor group in shear is designed according to ACI 318 14 – 17.5.2.

\[ \phi V_{cbg} = \phi \frac{A_V}{A_{Vo}} \psi_{ec,V} \psi_{ed,V} \psi_{c,V} \psi_{h,V} \psi_{\alpha,V} V_b \]

where:

ϕ = 0.65 – strength reduction factor for anchors in shear according to ACI 318-14 – 17.3.3, editable in Code setup
A_v – projected concrete failure area of an anchor or group of anchors
A_vo – projected concrete failure area of one anchor when not limited by corner influences, spacing, or member thickness
\( \psi_{ec,V} = \frac{1}{1+\frac{2 e'_V}{3 c_{a1}}} \) – modification factor for anchor groups loaded eccentrically in shear
\( \psi_{ed,V} = 0.7 + 0.3 \frac{c_{a2}}{1.5 c_{a1}} \le 1.0 \) – modification factor for edge effect
Ψ_c,V – modification factor for concrete condition; Ψ_c,V = 1.0 for cracked concrete, Ψ_c,V = 1.4 for non-cracked concrete
\( \psi_{h,V} = \sqrt{\frac{1.5 c_{a1}}{h_a}} \ge 1 \) – modification factor for anchors located in a concrete member where h_a < 1.5 c_a1
\( \psi_{\alpha ,V} = \sqrt{\frac{1}{(\cos \alpha_V )^2 + (0.5 \sin \alpha_V)^2}} \) – modification factor for anchors loaded at an angle 90° − α_V with the concrete edge; in ACI 318-14 – 17.5.2.1 are only discrete values, equation is taken from FIB bulletin 58 – Design of anchorages in concrete (2011)
h_a – height of a failure surface on the concrete side
\( V_b = \min \left ( 7 \left ( \frac{l_e}{d_a} \right )^{0.2} \lambda_a \sqrt{d_a} \sqrt{f'_c} c_{a1}^{1.5}, 9 \lambda_a \sqrt{d_a} \sqrt{f'_c} c_{a1}^{1.5} \right ) \)
l_e = h_ef ≤ 8 d_a – load-bearing length of the anchor in shear
d_a – anchor diameter
f'_c – concrete compressive strength
c_a1 – edge distance in the direction of load; according to Cl. 17.5.2.4, for a narrow member, c_2,max < 1.5 c₁ that is also deemed to be thin, h_a < 1.5 c₁, c'₁ is used in previous equations instead of c₁; the reduced c'₁ = max (c_2,max / 1.5, h_a / 1.5, s_c,max / 3)
c_a2 – edge distance in the direction perpendicular to load
c_2,max – largest edge distance in the direction perpendicular to load
s_c,max – maximum spacing perpendicular to direction of shear, between anchors within a group

If c_a2 ≤ 1.5 c_a1 and h_a ≤ 1.5 c_a1, \( c_{a1}= \max \left ( \frac{c_{a2}}{1.5}, \frac{h_a}{1.5}, \frac{s}{3} \right ) \), where s is the maximum spacing perpendicular to direction of shear, between anchors within a group.

According to ACI 318-14 – 17-5.2.9, where anchor reinforcement is developed in accordance with ACI 318-14 – 25 on both sides of the breakout surface, the anchor reinforcement is presumed to transfer the shear forces and concrete breakout strength is not evaluated.

Concrete pryout strength of anchor in shear

Concrete pryout strength is designed according to ACI 318-14 – 17.5.3.

ϕV_cp = ϕk_cp N_cp

where:

ϕ = 0.65 – strength reduction factor for anchors in shear according to ACI 318-14 – 17.3.3, editable in Code setup
k_cp = 1.0 for h^ef < 2.5 in., k_cp = 2.0 for h_ef ≥ 2.5 in
N_cp = N_cb (concrete breakout strength – all anchors are assumed in tension) in case of cast-in anchors

Interaction of tensile and shear forces

Interaction of tensile and shear forces is assessed according to ACI 318-14 – R17.6.

\[ \left ( \frac{N_{ua}}{N_n} \right )^{\zeta} + \left ( \frac{V_{ua}}{V_n} \right )^{\zeta} \le 1.0 \]

where:

N_ua and V_ua – design forces acting on an anchor
N_n and V_n – the lowest design strengths determined from all appropriate failure modes
ς = 5 / 3

Anchors with stand-off

The bar element is designed according to AISC 360-16. Interaction of shear force is neglected because the minimum length of the anchor to fit the nut under the base plate ensures that the anchor fails in bending before the shear force reaches half the shear resistance, and the shear interaction is negligible (up to 7 %). Interaction of bending moment and compressive or tensile force is conservatively assumed as linear. Second order effects are not taken into account.

Shear resistance (AISC 360-16 – G):

\( V_n = \frac{0.6 A_V F_y}{\Omega_V} \) (ASD)

\( V_n = \phi_V 0.6 A_V F_y \) (LRFD)

A_V = 0.844 ∙ A_s – the shear area
A_s – bolt area reduced by threads
F_y – bolt yield strength
Ω_V – safety factor, recommended value is 2
ϕ_V – resistance factor, recommended value is 0.75

Tensile resistance (AISC 360-16 – D2):

\( P_n = \frac{A_s F_y}{\Omega_t} \) (ASD)

\( P_n = \phi_t A_s F_y \) (LRFD)

Ω_t – safety factor, recommended value is 2
ϕ_t – resistance factor, recommended value is 0.75

Compressive resistance (AISC 360-16 – E3)

\( P_n = \frac{F_{cr} A_s}{\Omega_c} \) (ASD)

\( P_n = \phi_c F_{cr} A_s \) (LRFD)

\( F_{cr} = 0.658^{\frac{F_y}{F_e}} F_y \) for \( \frac{L_c}{r} \le 4.74 \sqrt{\frac{E}{F_y}} \), \( F_{cr} = 0.877 F_e \) for \( \frac{L_c}{r} > 4.74 \sqrt{\frac{E}{F_y}} \) – critical stress
\( F_e = \frac{\pi^2 E} {\left ( \frac{L_c}{r} \right) ^2} \) – elastic buckling stress
L_c = 2 ∙ l – buckling length
l – length of the bolt element equal to half the base plate thickness + gap + half the bolt diameter
\( r= \sqrt{\frac{I}{A_s}} \) – radius of gyration of the anchor bolt
\( I= \frac{\pi d_s^4}{64} \) – moment of inertia of the bolt
Ω_c – safety factor, recommended value is 2
ϕ_c – resistance factor, recommended value is 0.75

Bending resistance (AISC 360-16 – F11):

\( M_n = \frac{Z F_y}{\Omega_b} \le \frac{1.6 S_x F_y}{\Omega_b} \) (ASD)

\( M_n = \phi_b Z F_y \le 1.6 \phi_b S_x F_y \) (ASD)

\( Z = \frac{d_s^3}{6} \) – plastic section modulus of the bolt
\( S_x= \frac{2 I}{d_s} \) – elastic section modulus of the bolt
Ω_c – safety factor, recommended value is 2
ϕ_c – resistance factor, recommended value is 0.75

Linear interaction:

\[ \frac{N}{P_n}+\frac{M}{M_n} \le 1 \]

N – the tensile (positive) or compressive (negative sign) factored force
P_n – the tensile (positive) or compressive (negative sign) design or allowable strength
M – the factored bending moment
M_n – the design or allowable bending resistance