Learning Module: Load Path and Failure Modes of Fixed connections (EN)

Connection design can be difficult to teach, given the detailed nature of the topic and the fundamentally three-dimensional behavior of most connections. However, connections are critically important, and lessons learned in the study of connection design, including load path and identification and evaluation of failure modes, are general and applicable to structural design broadly. IDEA StatiCa uses a rigorous nonlinear analysis model and has an easy-to-use interface with a three-dimensional display of results (e.g., deformed shape, stress, plastic strain) and thus is well suited for the exploration of the behavior of structural steel connections. Building on these strengths, a suite of guided exercises that use IDEA StatiCa as a virtual laboratory to help students learn about concepts in structural steel connection behavior and design was developed. These learning modules were primarily targeted to advanced undergraduate and graduate students but were made suitable for practicing engineers as well. The learning modules were developed by Associate Professor Mark D. Denavit from the University of Tennessee, Knoxville.

This learning module is derived from Learning Module: Load Path and Failure Modes of Fully Restrained Moment Connections (AISC) and modified for Eurocode by Assistant Professor Martin Vild from Brno university of Technology.

Learning Objective

After performing this exercise, the learner should be able to describe the load path for a fixed connection and identify relevant failure modes.

Background

Load Path

Loads applied to a structure are transferred through members and connections before eventually being resisted by the ground. Tracking the path of the load from its point of load application to the ground can be a helpful qualitative exercise to ensure the path is continuous, and that each component along the path has sufficient stiffness and strength. Tracking a subset of the load path through a connection provides the same benefits.

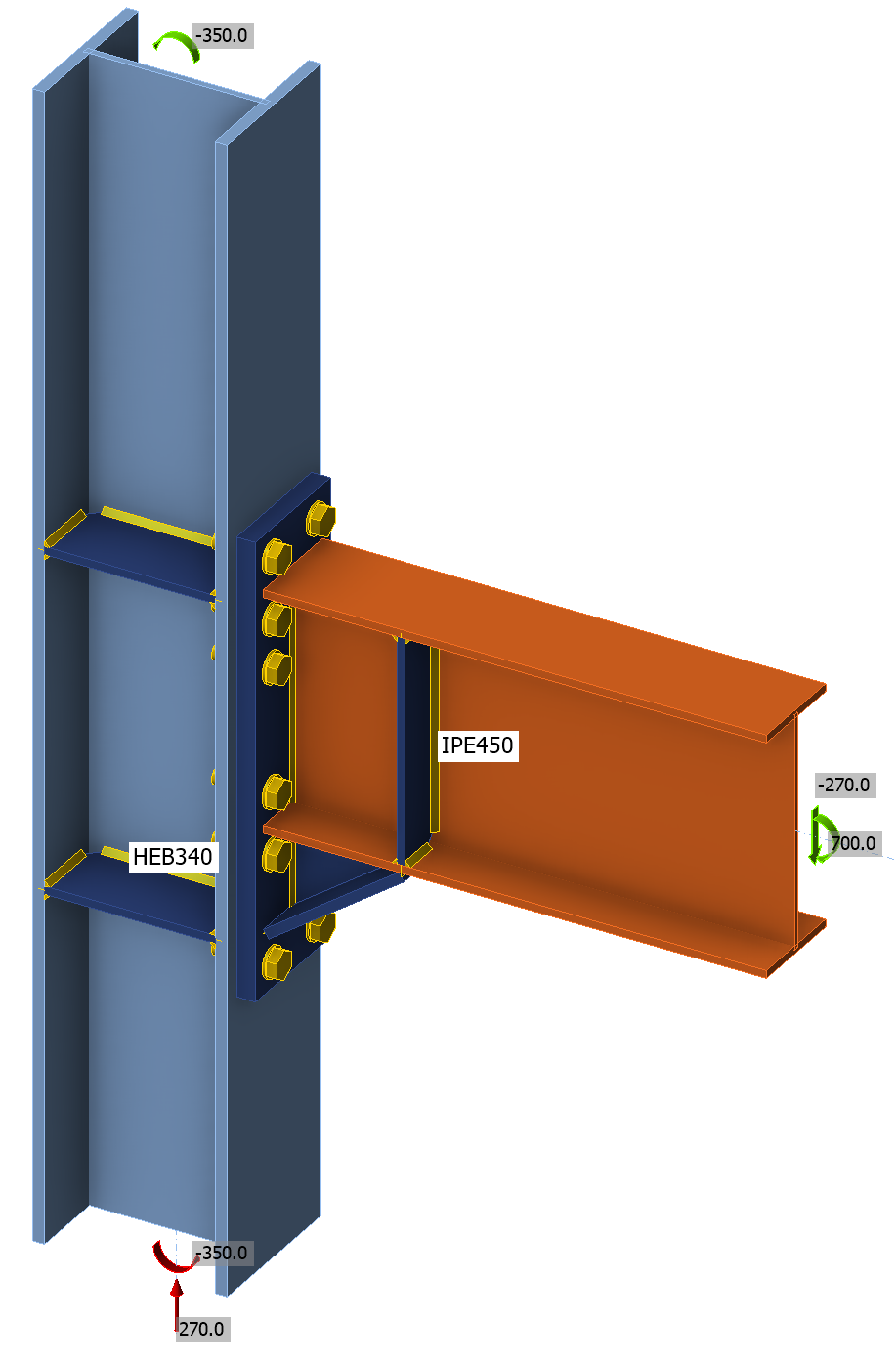
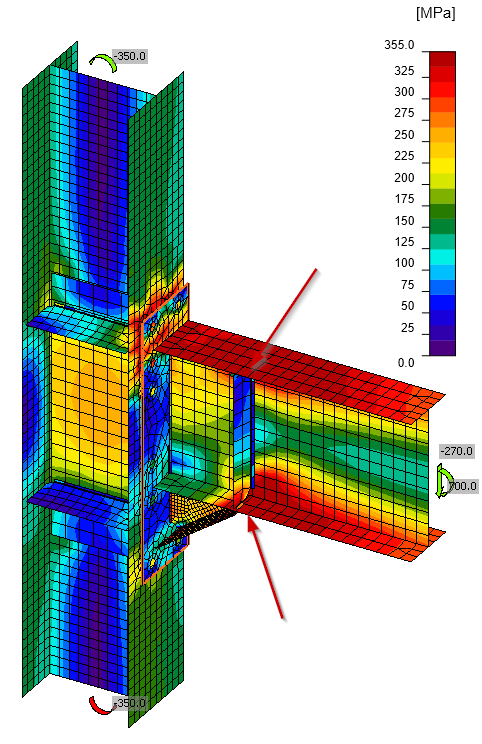
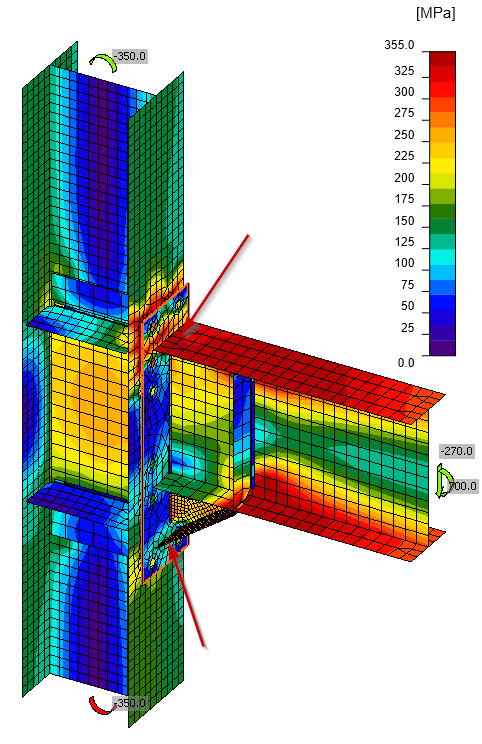
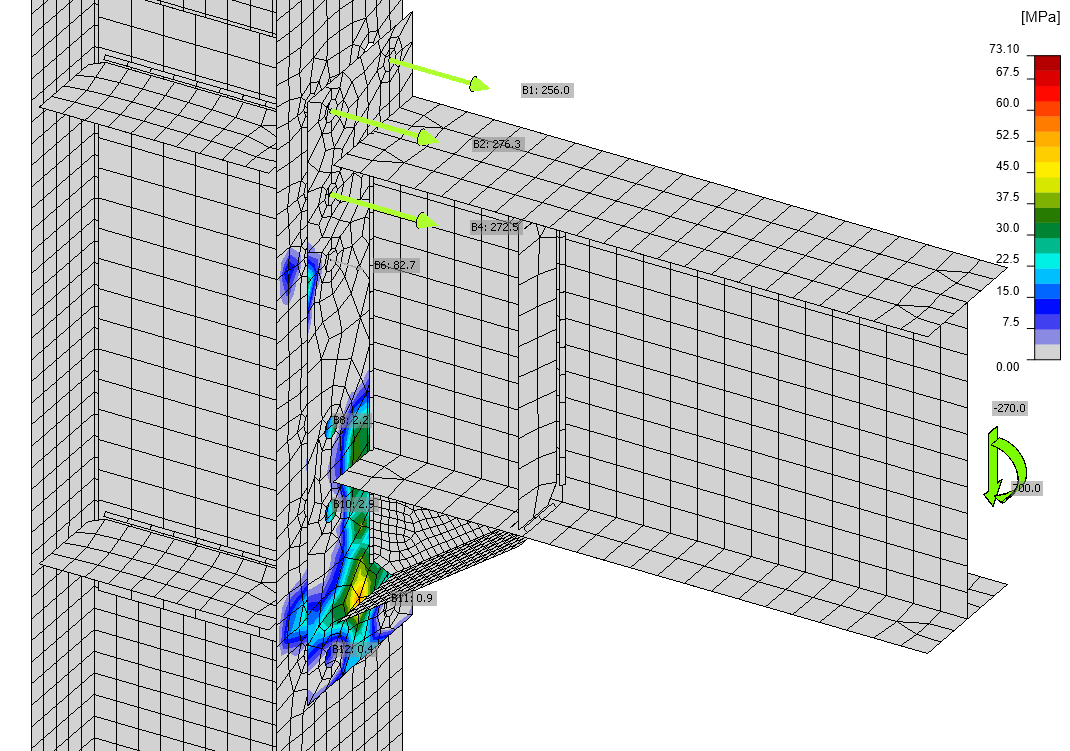
Consider, for example, the steel I-section beam-to-column fixed connection shown below. This connection is inspired by Equaljoints project for seismic applications. Moment in the beam is transferred to the column as follows:

• At the end of the beam, moment concentrates to the beam flanges, which are then subject to tension and compression.
• The haunch is added to increase the lever arm and thus the bending resistance. The bending moment is the highest in the node, and thanks to the shear force, it continually decreases. The stresses due to bending moment flow primarily through the top flange and the flange of the haunch.
• The shear stress flows through the beam web and the haunch web where the stiffness against vertical load is the highest.
• From the beam and the haunch, the load is distributed into the end plate by butt welds.
• The beam flange to column flange welds transfer the beam flange forces to the column flange.
• The shear force is transferred via shear in bolts to the column flange and the bending moment via the lever arm of two forces – tension through the bolt tension in the bolt rows near the top flange and compression via contact between end plate and the column flange.
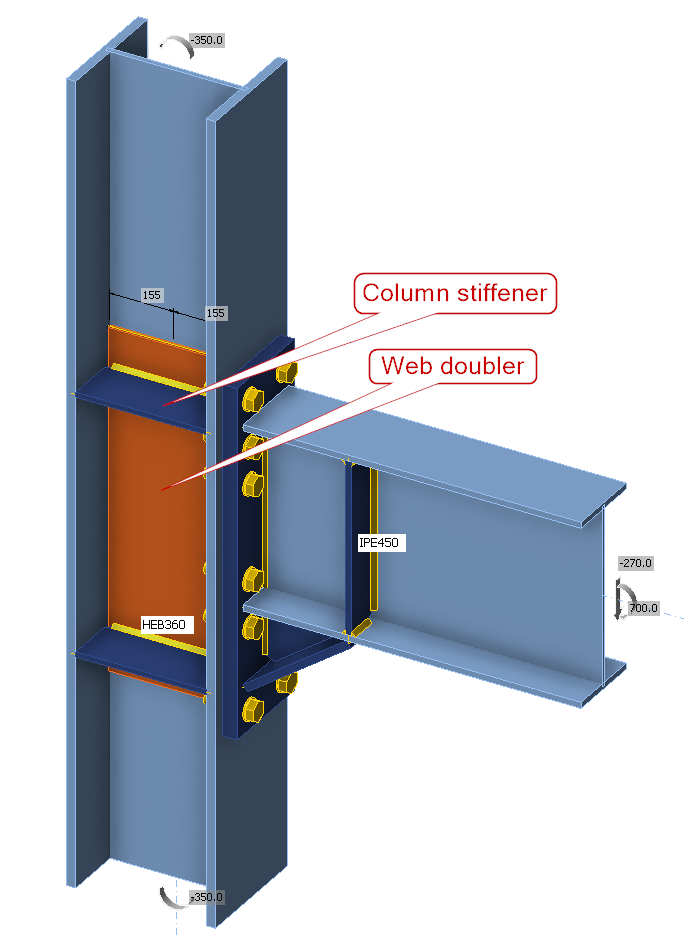
• Column stiffeners add to the strength and stiffness of the column against concentrated loads where they are expected to be the highest, i.e. at the beam top flange and hauch bottom flange. 
• The load from end plate bolts and stiffener welds spreads through the column cross-section, resulting in shear in the panel zone and moment in the column.

In traditional connection design, load paths such as this can help engineers develop a checklist of limit states and to ensure every step along the path has sufficient stiffness and strength. In design by inelastic analysis, load paths can help engineers by providing a mental model of connection behavior against which the results of numerical analyses can be compared.

Moment Connections

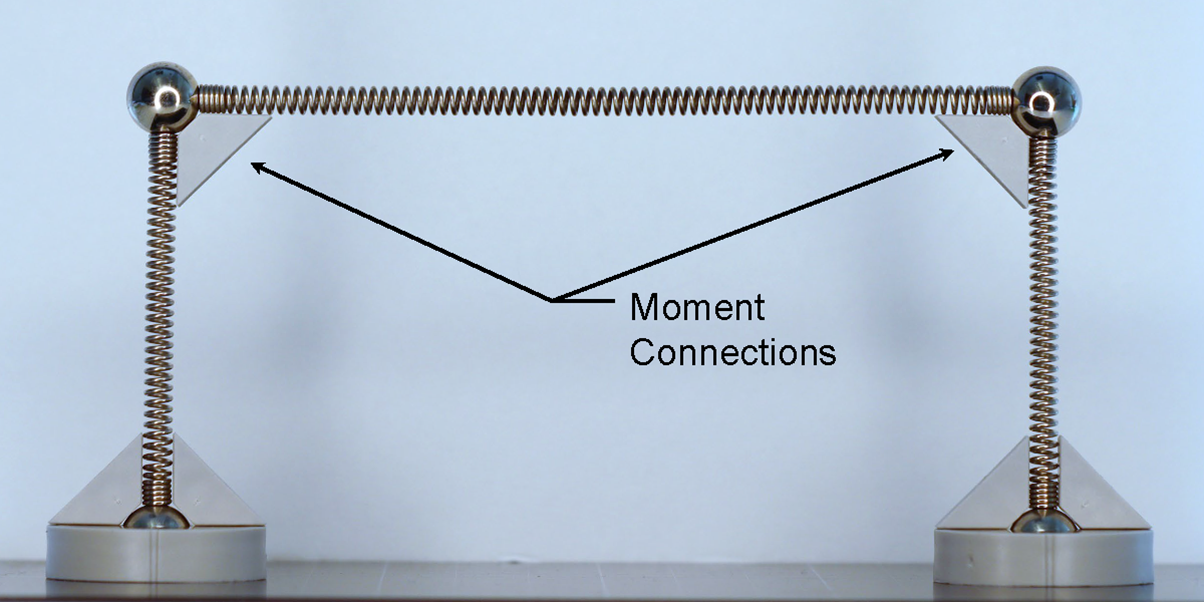
One of the major classifications of connections at the ends of beams is based on rotational stiffness. Simple shear connections are flexible enough to assume no moment is transmitted through the connection. Moment connections, on the other hand, transmit moment between the beam and column. Fully restrained connections are stiff enough to assume that no relative rotation occurs between members when transmitting the moment. Moment connections enable the beams and columns to form a moment frame that can serve as a lateral load-resisting system.

Moment frame action demonstrated with components from a Mola Structural Kit

Since most of the moment in a wide flange beam is resisted by the flanges, moment connections must engage the flanges of the beam directly. Moment connections typically also transfer shear or other forces from the beam to the column and thus also typically engage the web of the beam directly too. As a result, moment connections are generally statically indeterminate and the true distribution of stresses in the connection depends on the relative stiffness of the various components.

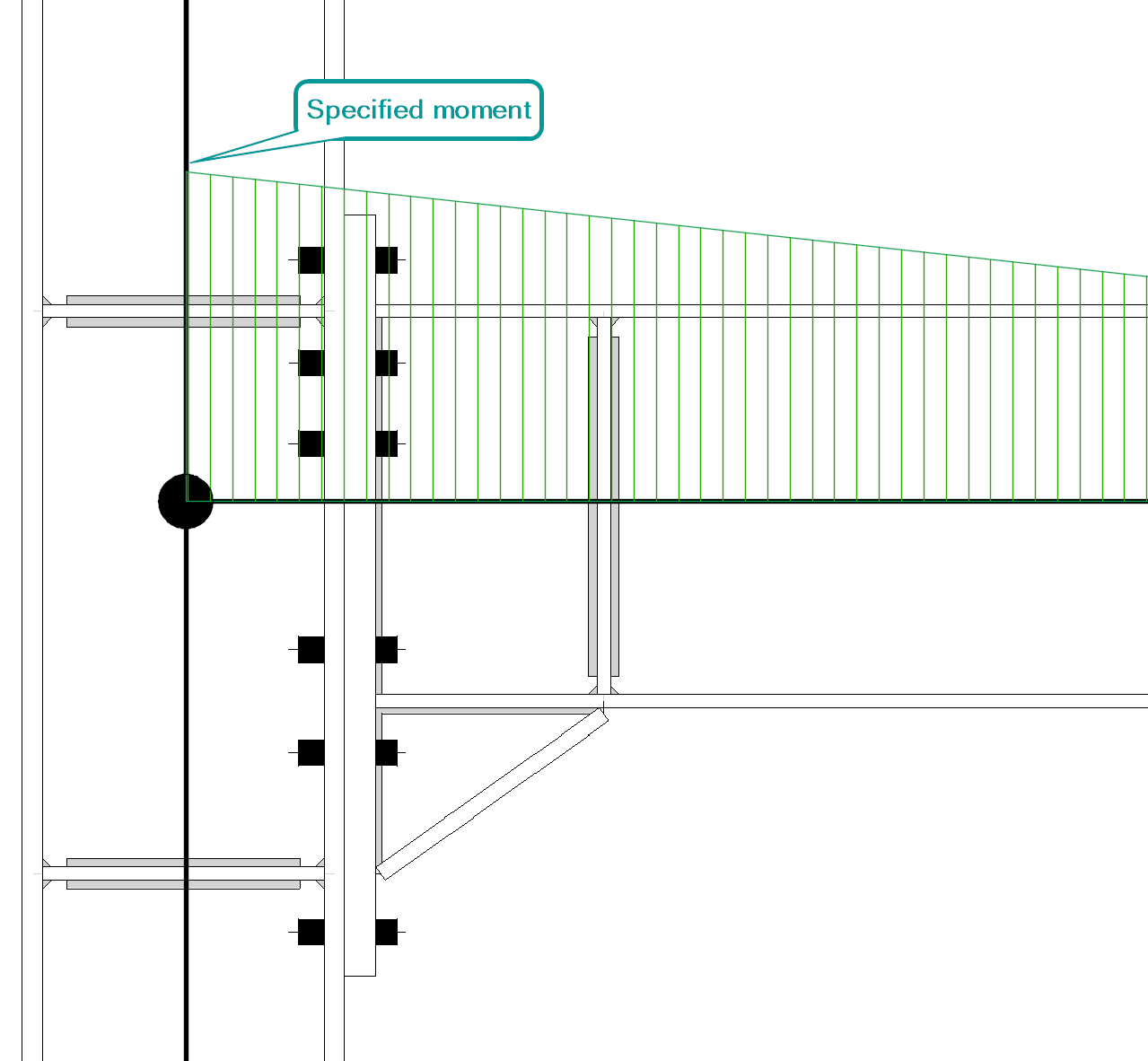
Shear forces induce a moment gradient in the beam. For moment connections, such as flange plate connections, that occur over a length of the beam, the moment is not constant. In hand calculations, the moment gradient is often conservatively neglected, and a single value of moment is used regardless of the length of the connection. The moment gradient cannot be neglected in IDEA StatiCa since the analyses ensure equilibrium and thus must be properly defined to be consistent with the structural analysis from which the required strengths were obtained. The specified moment will occur where defined by the “Forces in” option in the member menu.

Connection

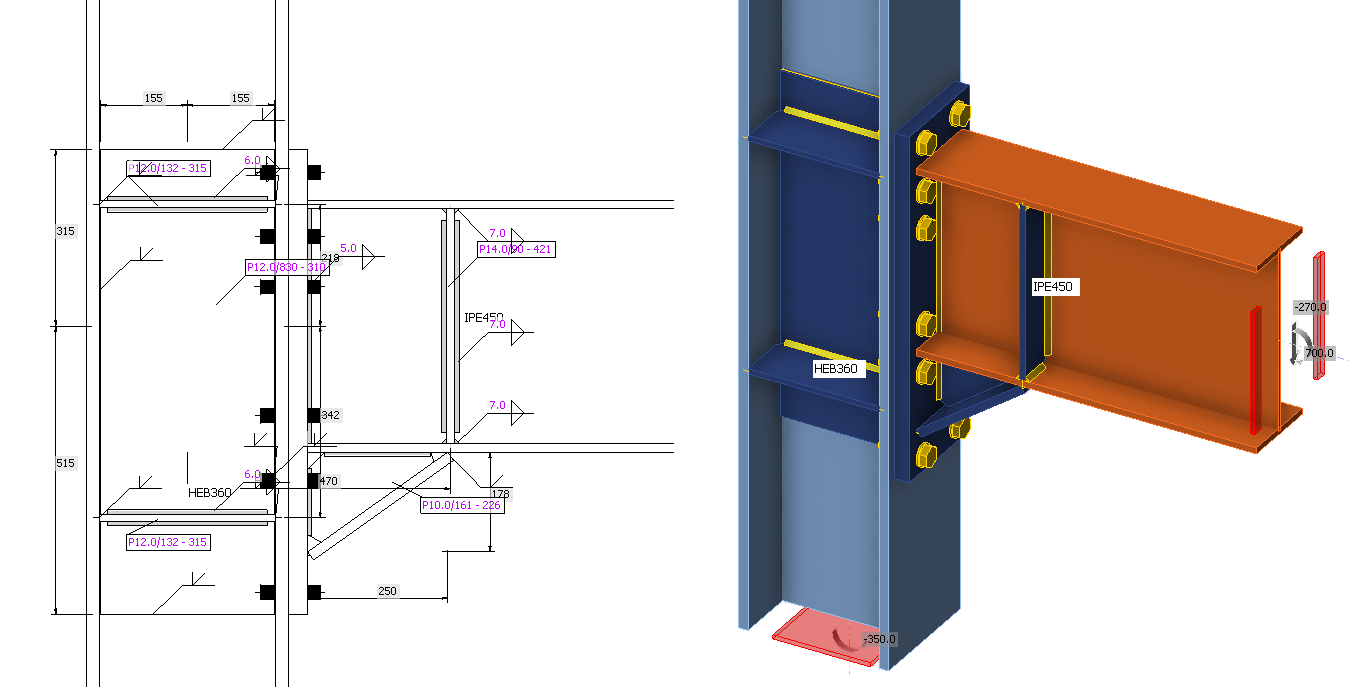
The examined connections are inspired by Equaljoints project. The haunched joint is selected for the first connection.

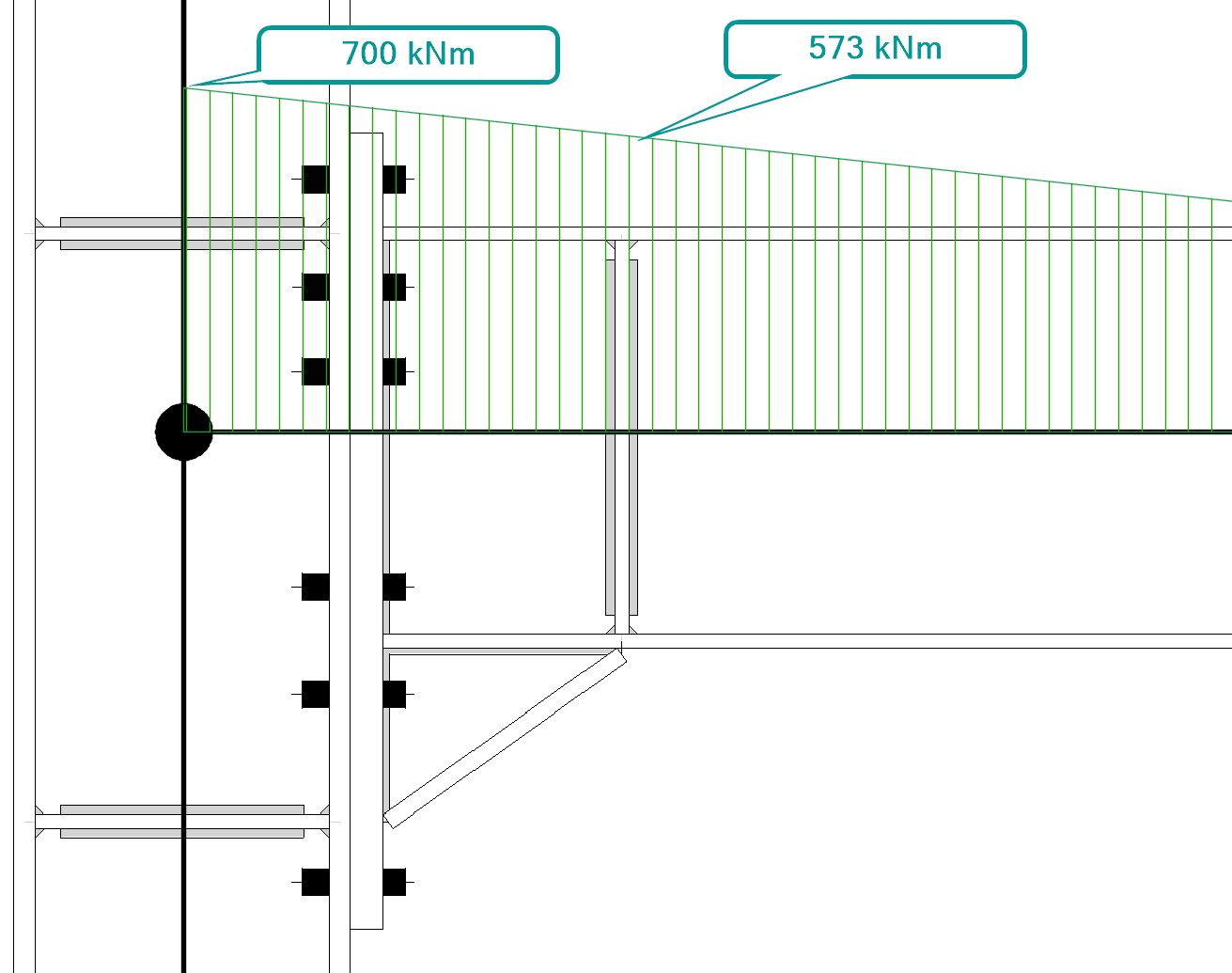
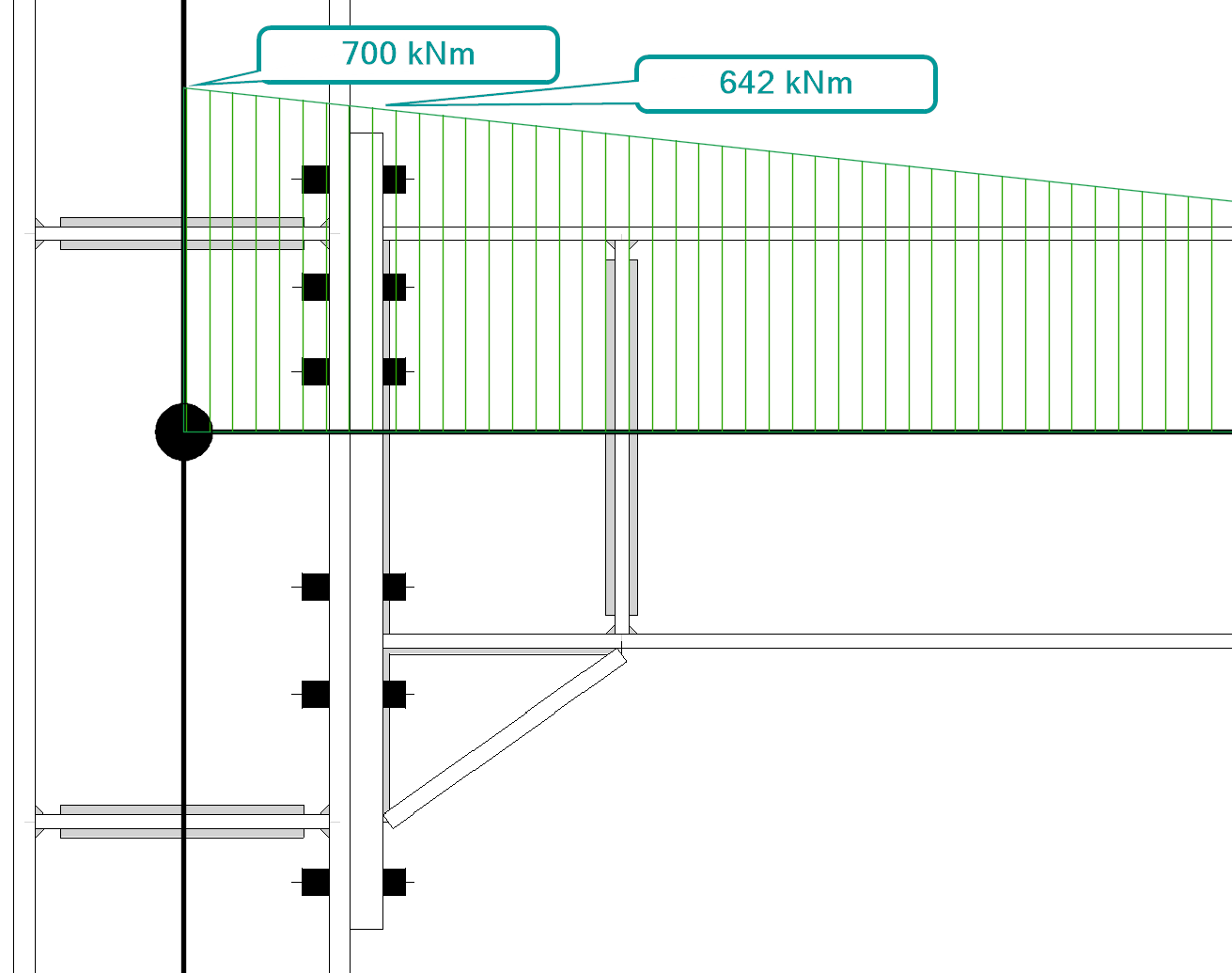
This connection is loaded by design shear force 270 kN and design bending moment 700 kNm. The loads are specified in node.

Procedure

The procedure for this exercise assumes that the learner has a working knowledge of how to use IDEA StatiCa (e.g., how to navigate the software, define and edit operations, perform analyses, and look up results). Guidance for how to develop such knowledge is available on the IDEA StatiCa website.

Retrieve the IDEA StatiCa file for the example connection provided with this exercise. Open the file in IDEA StatiCa. To perform the exercise, follow the narrative, complete the tasks, and answer the questions. Note that the design example can be helpful when answering the questions.

Load Path

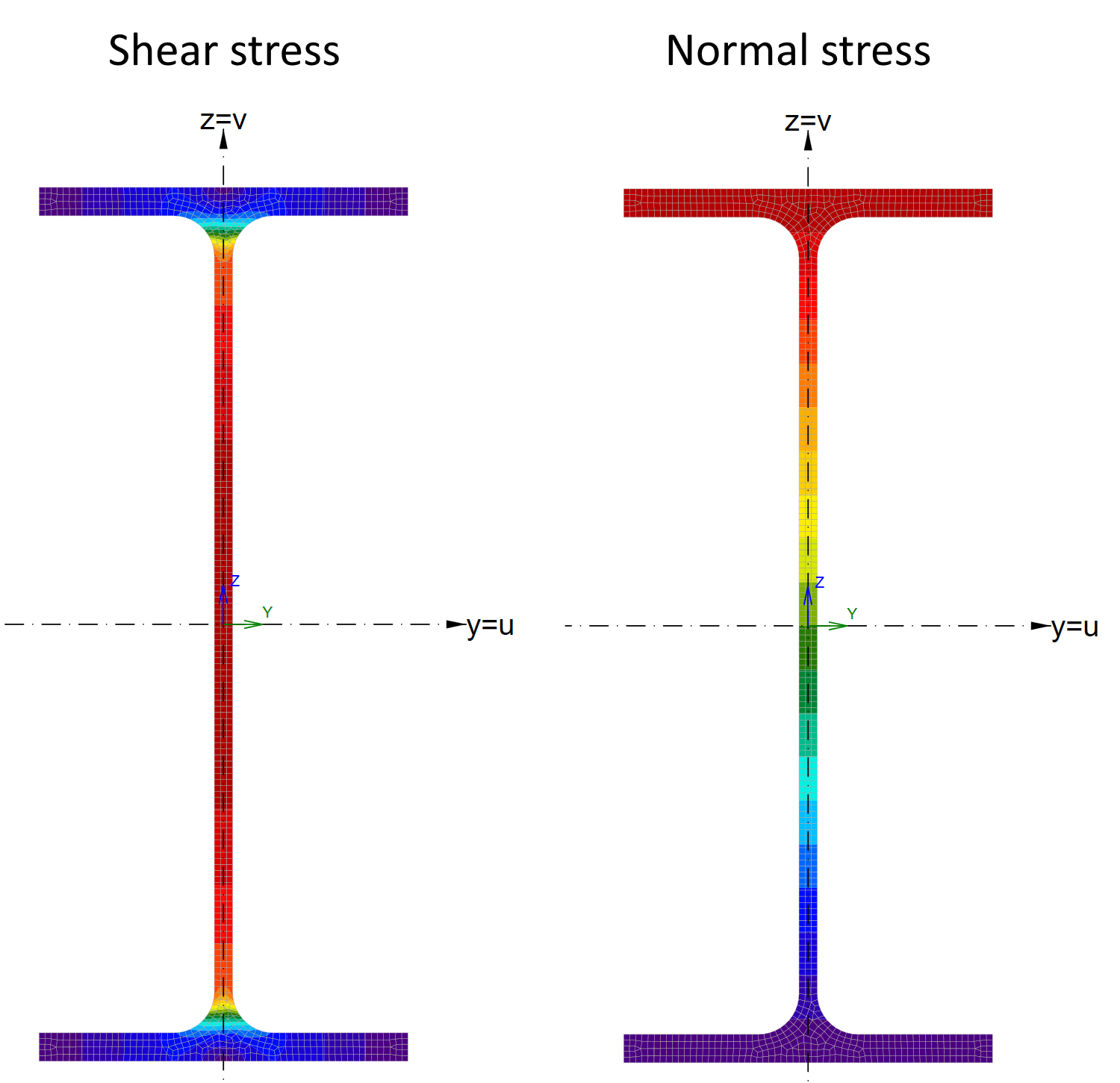
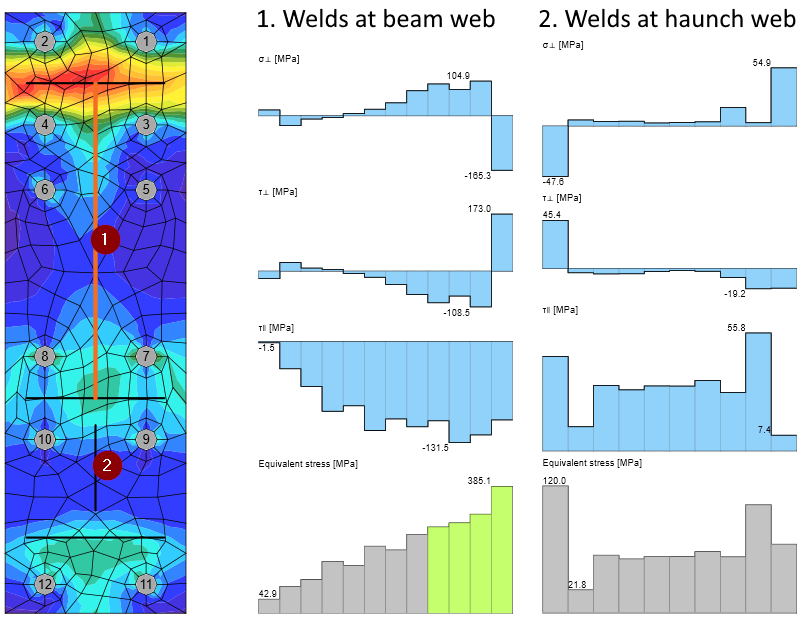
The load path for shear transferring from the beam to the column is as follows:

• Shear is concentrated at the beam web.
• Shear flows through welds by shear perpendicular stresses, \(\tau_\perp\), to the end plate.
• Through the end plate, the load is distributed into the bolts.
• Via shear stresses in bolts, the shear is transferred to the column flange and then by normal force in the column into the ground.

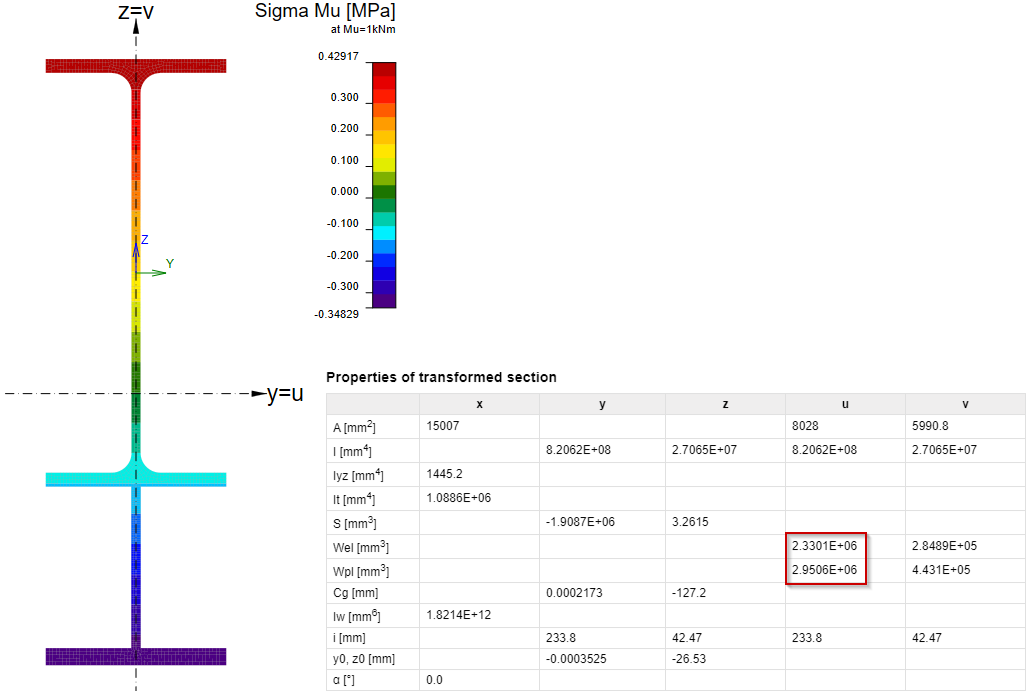
Shear stresses caused by unit shear force and normal stresses caused by unit bending moment at elastic stage

The load path for the bending moment transferring from the beam to the column is as follows:

• Moment concentrates mostly to the beam flanges, which are then subject to tension and compression.
• The haunch is added to increase the lever arm and thus the bending resistance. The bending moment is the highest in the node, and thanks to the shear force, it continually decreases. The stresses due to bending moment flow primarily through the top flange and the flange of the haunch.
• From the beam and the haunch, the load is distributed into the end plate by butt welds.
• The beam flange to column flange welds transfer the beam flange forces to the column flange.
• The bending moment is transferred via the lever arm of two forces – tension through the bolt tension in the bolt rows near the top flange and compression via contact between end plate and the column flange.
• Column stiffeners add to the strength and stiffness of the column against concentrated loads where they are expected to be the highest, i.e. at the beam top flange and hauch bottom flange. 
• The load from end plate bolts and stiffener welds spreads through the column cross-section, resulting in shear in the panel zone and moment in the column.

Beam

The beam is subject to moment; therefore, failure modes such as flexural yielding and lateral-torsional buckling must be investigated as part of the member evaluation. The effect of lateral-torsional buckling may be checked in IDEA StatiCa Member using GMNIA or by code calculation according to EN 1993-1-1 – Cl. 6.3.2. Flexural yielding is in IDEA StatiCa checked against the 5% plastic strain limit. The most dangerous cross-section is at the end of the haunch.

What is the bending moment at the beam just before the beginning of the haunch? Compare the stress in the beam flanges with IDEA StatiCa.

The distance to the start of the haunch is:

\[ h_c/2+t_p+b_h = 360/2+35+255 = 470 \textrm{ mm} \]

And the bending moment:

\[ M_{Ed} + 0.470 \cdot V_{Ed} = 700 + 0.470 \cdot (-270) = 573.1 \textrm{ kNm} \]

The stress in the beam can be calculated using elastic or plastic section modulus. Using elastic section modulus, we obtain:

\[ M_{Ed} / W_{el,y} = 573.1 \cdot 10^6/ 1.5\cdot 10^6 = 382 \textrm{ MPa}\]

This is higher than the yield strength, which means the flanges must already yield.

Using plastic section modulus:

\[ M_{Ed} / W_{pl,y} = 573.1 \cdot 10^6/ 1.7\cdot 10^6 = 337 \textrm{ MPa}\]

This is below yield strength. The cross-section is yielding but is not fully plasticized. We can expect 355 MPa at flanges and an elasto-plastic stress distribution in the web.

Note that uniaxial longitudinal stress is equal to equivalent stress shown by IDEA StatiCa. The stresses confirm our calculations.

Haunch

Haunch increases the beam cross-section, increasing connection strength and stiffness by increasing lever arm between tension in bolts and the compression center.

What is the bending moment at the connection between haunch and end plate? What are the stresses in the haunch at this location (use simplified calculation)? Compare the calculated stresses to IDEA StatiCa.

The bending moment at the haunch end is:

\[ M_{Ed} + (h_c/2+t_p) \cdot V_{Ed} = 700 + (0.36/2+0.035) \cdot (-270) = 642 \textrm{ kNm}\]

The exact calculation of section modulus of beam and a haunch is relatively complicated. Plastic section modulus can be exactly calculated in general cross-section editor. In simplified calculation, we can neglect beam bottom flange and assume haunch web and flange thicknesses equal to beam web and flange thicknesses.

\[W_{pl,y} = 2 \cdot [(14.6 \cdot 190) \cdot (450+178)/2 +(450+178)/2 \cdot (450+178)/4)] = 1 840 668 \textrm{ mm}^3 \]

The stress at the haunch end is:

\[ \sigma = M_{Ed}/W_{pl,y} = 642 \cdot 10^6 / 1840668 = 349 \textrm{ MPa}\]

Again, we should expect yielding in flanges and not fully utilized web. This agrees well with IDEA StatiCa.

Stresses from unit bending moment and cross-sectional properties of the hauch just behind end plate

End plate

The shear and normal stresses are transferred into the end plate via welds. Full-penetration butt welds are used for critical welds of flanges. Fillet welds are used at the web where the welds are less loaded.

What direction of stresses do you expect in the fillet welds at beam web? What is the expected value of perpendicular shear stress in the fillet weld caused by the shear force?

There are several approaches we can use for designing welds at I-section.

• The most simple is to assume that welds at flanges take bending moments and welds at the web transfer shear force
• More accurate at the elastic stage is the assumption that weld group transfers the bending moment in ratio of moment of inertias, i.e.:

\[M_{flange} = I_{flange}/I_{total}\]

\[M_{web} = I_{web}/I_{total}\]

where: 

• M_flange – portion of bending moment transferred via flange welds
• M_web – portion of bending moment transferred via web welds
  • Note that \(M_{flange}+M_{web} = M_{total}\)
• I_flange – moment of inertia of flanges
• I_web – moment of inertia of web
• I_total – total moment of inertia
  • Note that \(I_{flange}+I_{web} = I_{total}\)

The shear force is assumed to be taken only by beam web.

So we can expect significant shear stresses parallel to the weld axis, \(\tau_\parallel\) and some normal and shear stresses, \(\sigma_\perp\) and \(\tau_\perp\) due to bending.

The magnitude of \(\tau_\parallel\) can be calculated by summing up the fillet weld areas at the beam web and the hauch web:

\[A_w = 2 \cdot 5 \cdot 421 + 2 \cdot 5 \cdot 118 = 5390\textrm{ mm}^2\]

Then we can calculate the expected uniform stress:

\[\tau_\parallel = V_{Ed} / A_w = 270 \cdot 10^3 / 5390=50 \textrm{ MPa}\]

Comparison to IDEA StatiCa results shows a complicated stress pattern exceeding the calculated value:

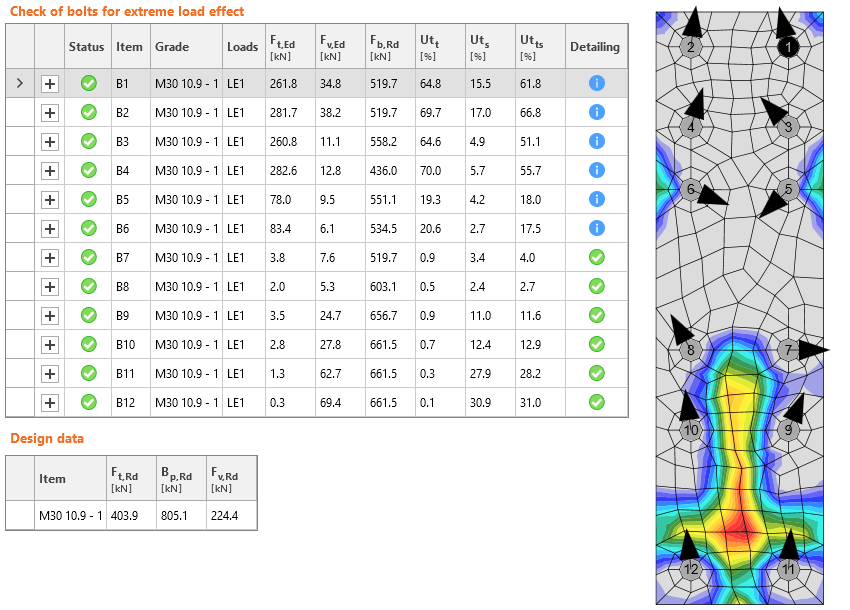
The load is transferred through the end plate into bolts. Typically, it is assumed that the shear forces are distributed evenly into all bolts. Alternatively, the bolts loaded most in tension are excluded and it is assumed that the bolts in compression zone transfer shear force.

Calculate shear force in bolts and compare to IDEA StatiCa.

\[F_{v,Ed} = V_{Ed} / n = 270 / 12 = 22.5 \textrm{ kN}\]

where:

• \(F_{v,Ed}\) – shear force in one bolt
• \(V_{Ed}\) – total shear force
• \(n\) – number of bolts

The forces in IDEA StatiCa are quite diverse, which is caused by a significant deformation of the column web in shear and end plate.

The first rows of bolts are loaded by tension and the end plate is in contact with column flange at the haunch flange. 

To calculate bending moment by hand, the tensile forces in bolts may be assumed plastically provided Clause 6.2.7.2 (9) is satisfied. Basically mode 1 or 2 (relatively thin end plate or column flange compared to bolts) should govern to ensure ductile behavior. 

Column

The load is transferred to the column via tensile and shear forces in end-plate bolts and via contact forces between end plate and column flange.

Try to remove column web stiffeners and column web doubler. Will the governing failure mode change?

Several operations should be deactivated:

The analysis stops at reaching weld resistance at 97% of applied load

General Procedure

For a more open-ended experience or for connections other than the haunch joint, complete the following tasks:

1. Select one of the connections described below.
   • Review the design example upon which the connection is based.
   • Retrieve the IDEA StatiCa file for the connection provided with this exercise. Open the file in IDEA StatiCa.
2. Describe the load path for this connection.
3. Answer the following questions for each step in the load path:
   • What is the required strength?
   • What failure modes need to be considered?
   • How are the failure modes considered in traditional calculations?
   • How are the failure modes considered in IDEA StatiCa?