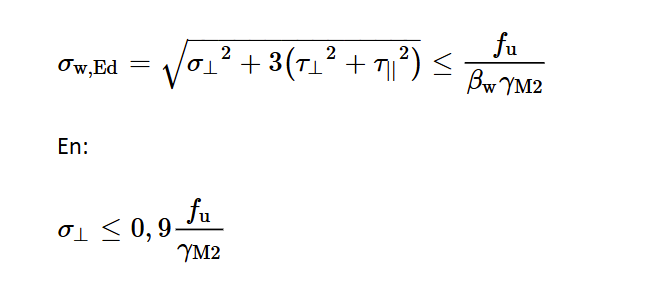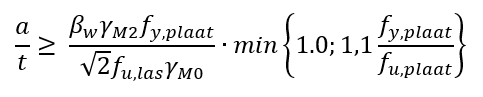Vragen als:
- Is een plastische verdeling in lassen toegestaan en in overeenstemming met de norm?
- Leidt de manier waarop lassen zijn gemodelleerd in IDEA niet tot een te hoge weerstand?
- Hoe wordt omgegaan met de eisen uit art. 4.9 van EN 1993-1-8 die stellen dat er niet hoort te zijn gerekend op de vervormingseigenschappen van de lassen?
- Hoe wordt omgegaan met de eis dat lassen voldoende sterk zijn zodat ze niet breken voordat het naastliggende moedermateriaal vloeit?
In dit artikel proberen we antwoord te geven op deze vragen.
Werkelijke gedrag van een las
Daarvoor is het goed om eerst het werkelijke gedrag van een las te beschouwen. De werkelijke spanningsverdeling c.q. rekverdeling in een hoeklas onder verschillende belastingcombinaties van krachten is echter moeilijk exact te bepalen. Daarbij komt dat in het moedermateriaal nabij de las en in de las zelf allerminst sprake is van homogene materiaaleigenschappen. Om toch inzicht te krijgen in het bezwijkgedrag van lassen zijn daarom wereldwijd een groot aantal proeven uitgevoerd.
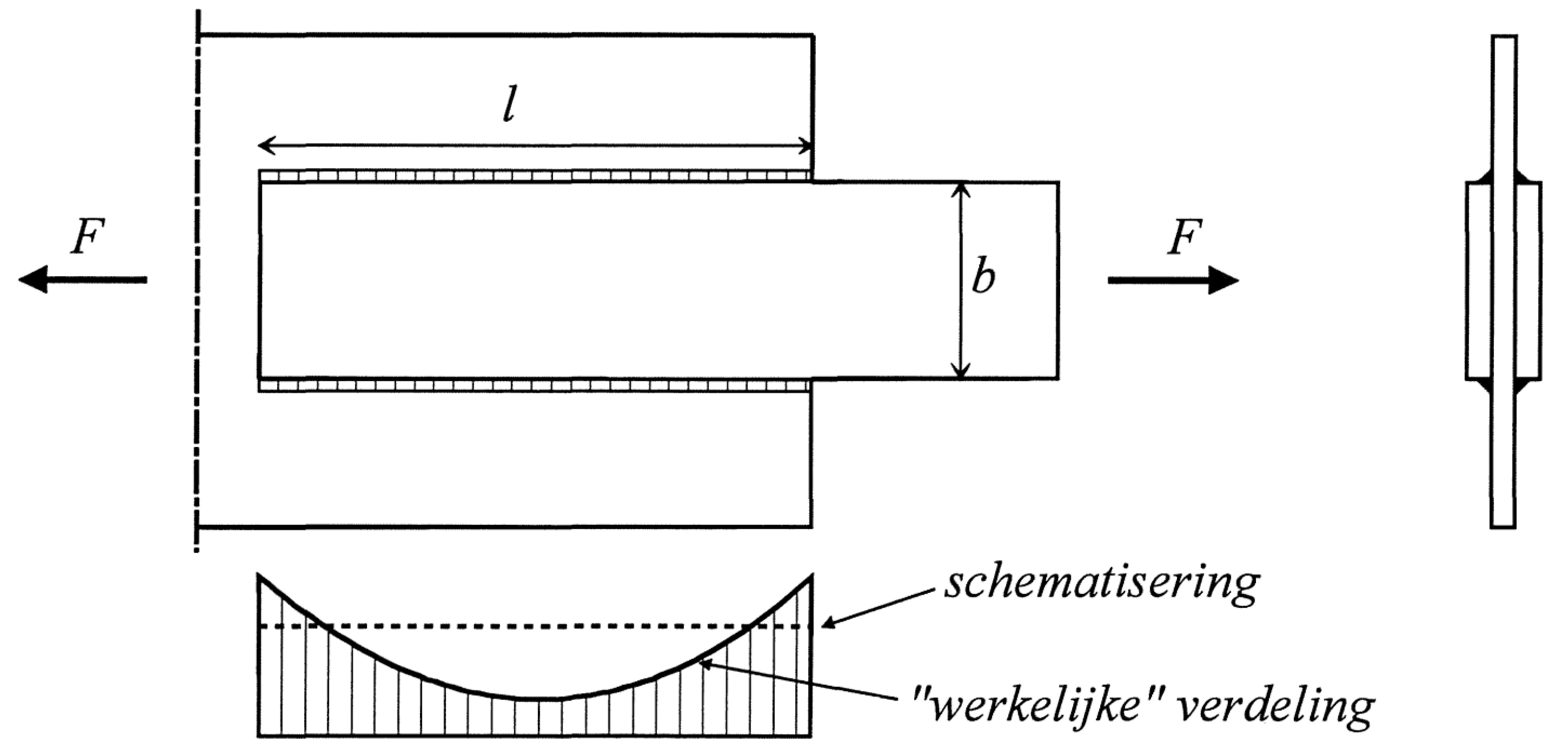
Neem bijvoorbeeld een flanklasverbinding die in lengterichting wordt belast. Analoog aan boutverbindingen die in lengte richting wordt belast, zal de spanningsverdeling niet gelijkmatig zijn. Toch kan men kwalitatief wel aangeven hoe het spanningsverloop zou zijn in de las. De hoogste spanningen treden op bij de einden.
Figuur 1 - Ongelijkmatige verdeling van de schuifspanning in een flanklasverbinding
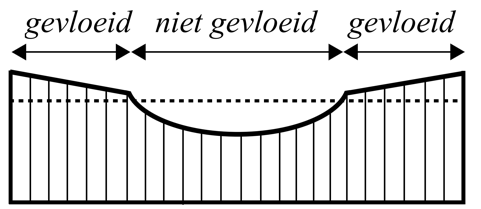
Bij verder doorbelasten blijkt dat de las wel degelijk een bepaalde mate van vervormingscapaciteit heeft en er lokaal vloeien kan optreden (Figuur 2).
Figuur 2 - Ongelijkmatige spanningsverdeling van de schuifspanning met lokaal vloeien in een flanklasverbinding
Eurocode methode
Andere lasconfiguraties en belastingcombinaties kunnen leiden tot andere spanningsverdelingen. Als basis voor de rekenregels uit de Eurocode is dan gekozen voor een semi-empirische benaderingswijze. In plaats van toetsing van het bezwijkfenomeen op microschaal wordt de las in zijn geheel op macroschaal getoetst. Hierbij is een vereenvoudigd bezwijkmodel aangenomen, dat gebaseerd is op de plasticiteitsleer. Door het terugrekenen van de proefresultaten is dan een bezwijkcriterium (lasformule) vastgesteld.
In EN 1993-1-8 art. 4.5.3 worden twee methodes gegevens voor de bepaling van de rekenwaarde van de weerstand van hoeklassen, de “gecombineerde spanningenmethode” en de “vereenvoudigde methode”. De vereenvoudigde methode is een vereenvoudigde methode van de gecombineerde spanningenmethode. In de gecombineerde spanningenmethode zijn de krachten die zijn overgedragen door een eenheidslengte van las ontbonden in spanningscomponenten σ⊥, σ||, τ⊥ en τ || in de keeldoorsnede van de las. De normaalspanning σ|| evenwijdig aan de lengte-as wordt echter niet beschouwd in de toetsing van de rekenwaarde van de weerstand van de las. De rekenwaarde van de weerstand van een hoeklas zal voldoen indien aan beide volgende voorwaarden voldaan is:
Waarin:
| σ⊥ | normaalspanning loodrecht op het vlak van de keeldoorsnede |
| τ⊥ | schuifspanning loodrecht op de lengte-as van de las |
| τ || | schuifspanning evenwijdig aan de lengte-as van de las |
| fu | nominale treksterkte van het zwakste verbonden onderdeel |
| βw | correlatiefactor afhankelijk van de treksterkte van het moedermateriaal |
| γM2 | partiële veiligheidsfactor voor bouten en lassen = 1,25 |
Bij de lasberekening van statisch belaste constructies mag dan, indien het evenwicht zich er niet tegen verzet, worden uitgegaan van een gelijkmatige spanningsverdeling over de dikte en lengte van de las. Er wordt hier echter ook impliciet van uitgegaan dat plastische rekken moeten kunnen optreden om herverdeling van de spanningen mogelijk te maken. De gevraagde vervormingscapaciteit is groter naarmate de laslengte l toeneemt. De rekcapaciteit blijft echter wel beperkt, zo zal volgens de norm (zie hoofdstuk 4.10 van EN 1993-1-8) in bepaalde situaties rekening gehouden moeten worden met een effectieve breedte beff, bijvoorbeeld bij de aansluiting van een strip (of een flens) aan een onverstijfd I-profiel (Figuur 3).
Figuur 3 - Effectieve breedte van een onverstijfde T-verbinding
CBFEM methode
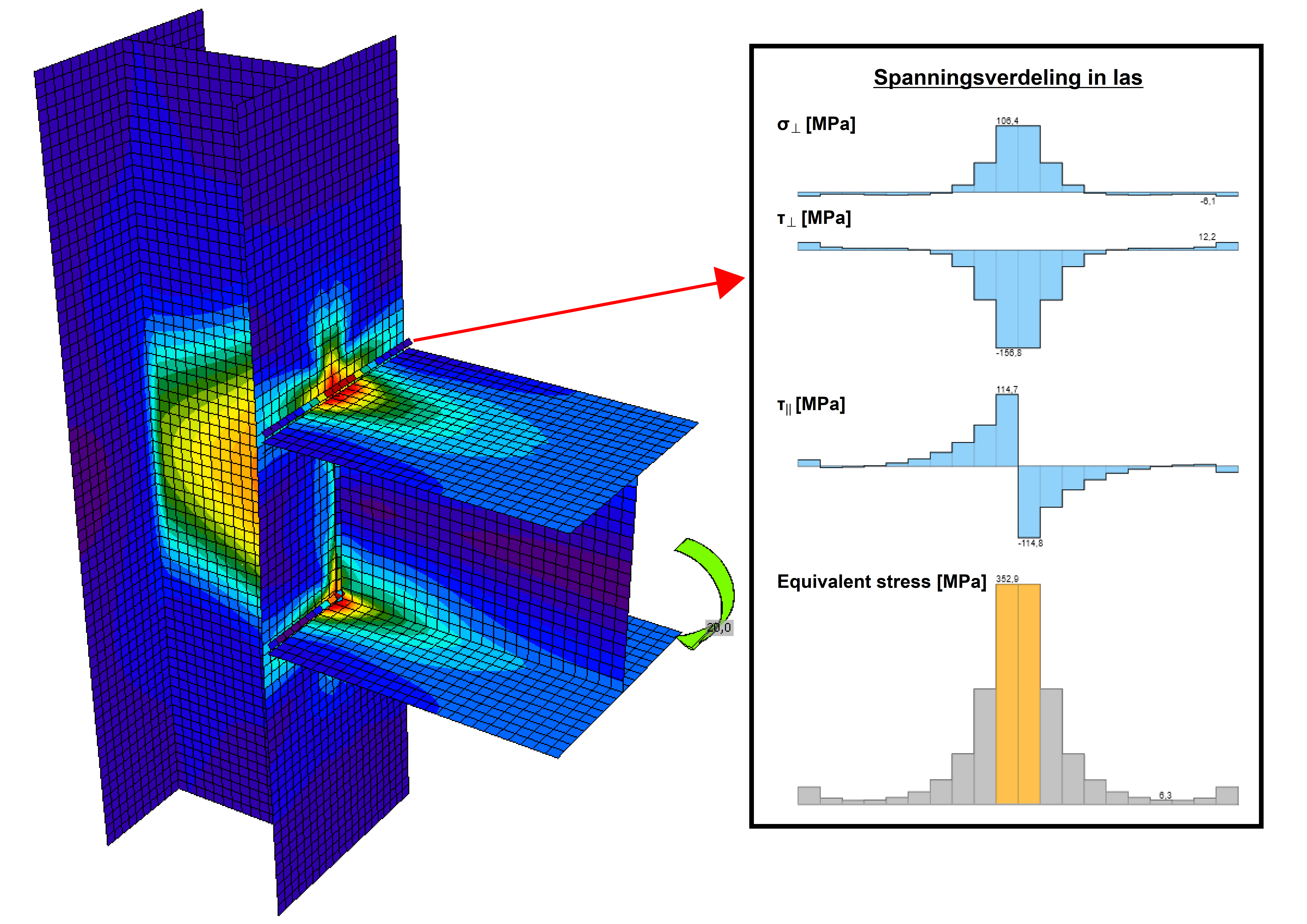
In het CBFEM (Component Based Finite Element Model) dat wordt toegepast in IDEA StatiCa, bestaat een las echter uit meerdere kleine elementjes naast elkaar. Daarbij wordt rekening gehouden met de toegekende lasdikte, positie en oriëntatie van de las. Spanningen en rekken in elk elementje van een las kunnen verschillend zijn. Hierdoor ontwikkelt zich automatisch een ongelijkmatige spanningsverdeling die realistischer is dan de geschematiseerde constante spanningsverdeling volgens de norm (Figuur 4).
Figuur 4 –Spanningen in platen en lassen in een gelaste kolom-ligger verbinding in IDEA
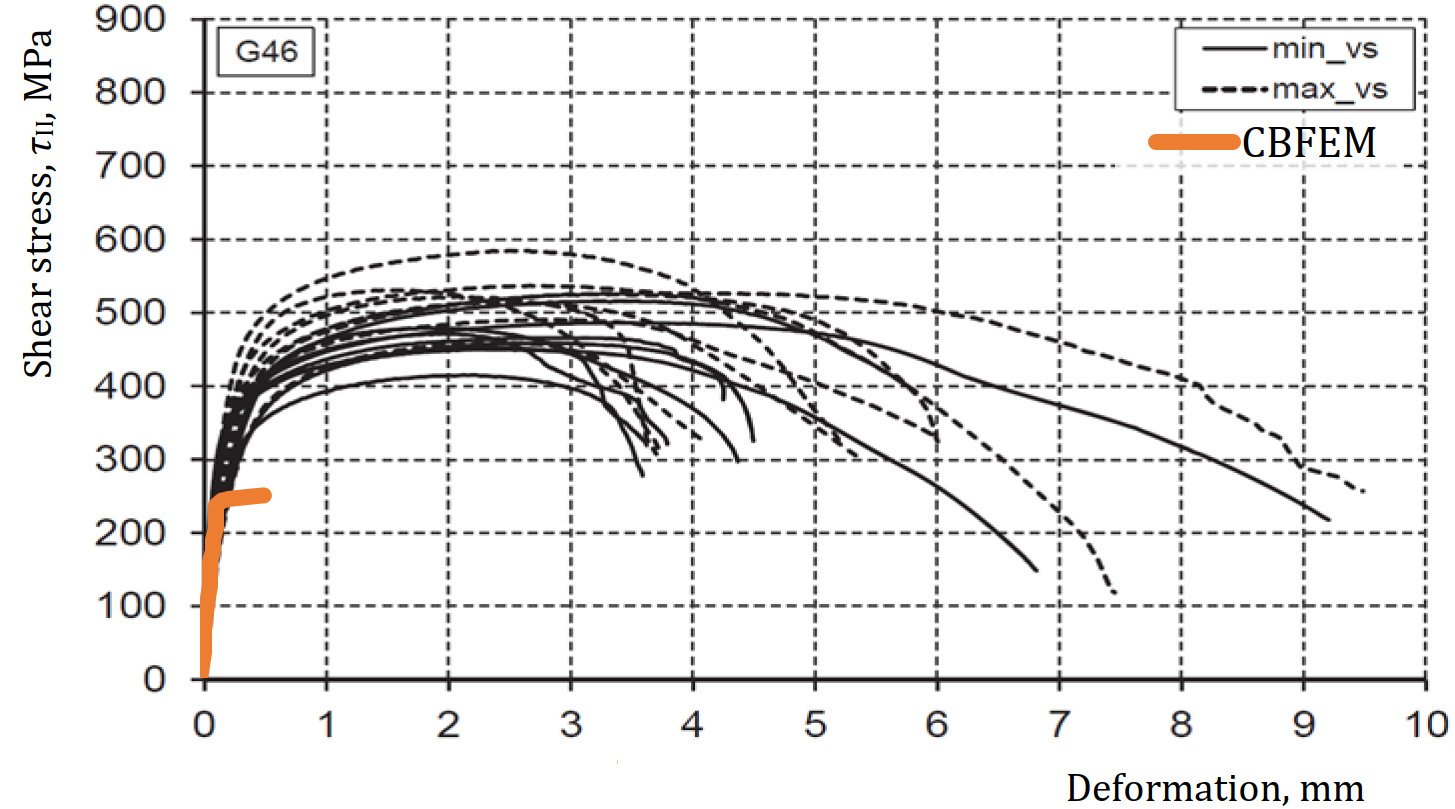
Het toegepaste materiaal model is echter alsnog niet bedoeld om het werkelijke gedrag perfect realistisch te simuleren. Restspanningen of krimp in de lassen zijn verwaarloosd. Het materiaalmodel met bijbehorende rekgrens is echter zo gekozen dat de totale weerstand van de las goed overeenkomt met de weerstand bepaald volgens de norm. Hiertoe heeft IDEA StatiCa veel validaties uitgevoerd. In het CBFEM boek (geschreven door prof. Frantisek Wald et al. van de Technische universiteit in Praag) en in verder aanvullend onderzoek zijn een groot aantal vergelijkingen gemaakt van verschillende type lassen berekend in IDEA StatiCa en lassen berekend volgens de norm of lassen beproefd in experimenten (zie Figuur 5). Op onze website zijn tal van validatie documenten hierover terug te vinden - support center verifications
Figuur 5 - Schuifspanning - vervorming diagrammen van proeven van Kleiner (2018) vergeleken met CBFEM
Hieruit volgt dat de gehanteerde rekgrens leidt tot een veilige totale weerstand van de las die ook goed overeenkomt met die berekend volgens de norm. Dit is de reden waarom een plastische herverdeling in het IDEA model acceptabel wordt geacht. Zonder plasticiteit in de lassen mee te nemen zou men nooit in de buurt kunnen komen van de weerstand zoals men die met de hand zou berekenen volgens de norm (die impliciet dus ook uitgaat van plastische herverdeling).
Aanvullende eisen uit EN 1993-1-8 art. 4.9
De EN 1993-1-8 stelt verder in art. 4.9(4) tot en met (6) nog een aantal aanvullende eisen aan lassen in verbindingen. Het idee achter deze regels is dat voorkomen moet worden dat een verbinding zonder waarschuwing bezwijkt. Zelfs als is aangetoond dat plastische rekken kunnen optreden in lassen, en de las in principe sterk genoeg is om de krachten (die zijn bepaald in een algemene statische berekening) over te brengen, kan het zo zijn dat er onverhoopt grotere belastingen optreden die leiden tot bezwijken en er toch onvoldoende waarschuwend effect is in de verbinding als geheel. Dit omdat de totale verlengingen van een las dan alsnog te klein kunnen zijn in absolute zin. Voldoende waarschuwend effect kan dan worden verkregen door de verbinding zo te ontwerpen dat een aangesloten plaat kan vloeien voordat de las breekt. Dit kan bereikt worden door een minimale lasdikte-plaatdikte verhouding aan te houden. Vandaar dat IDEA StatiCa ook detailleringschecks heeft ingebouwd om te toetsen op een minimale lasdikte bij een gegeven plaatdikte.
De specifieke regel die IDEA hanteert is gebaseerd op art. 6.9(4) uit de conceptversie van de aankomende nieuwe Eurocode (FprEN 1993-1-8:2023 (E)) die stelt dat om aan bovenstaande eis te voldoen de las zodanig moet zijn ontworpen dat de weerstand van de las ten minste gelijk is aan:
- 1,1 fy/fu keer de ontwerpweerstand van de zwakste aangesloten plaat
- maar hoeft niet meer te zijn dan de ontwerpweerstand van de zwakste aangesloten plaat
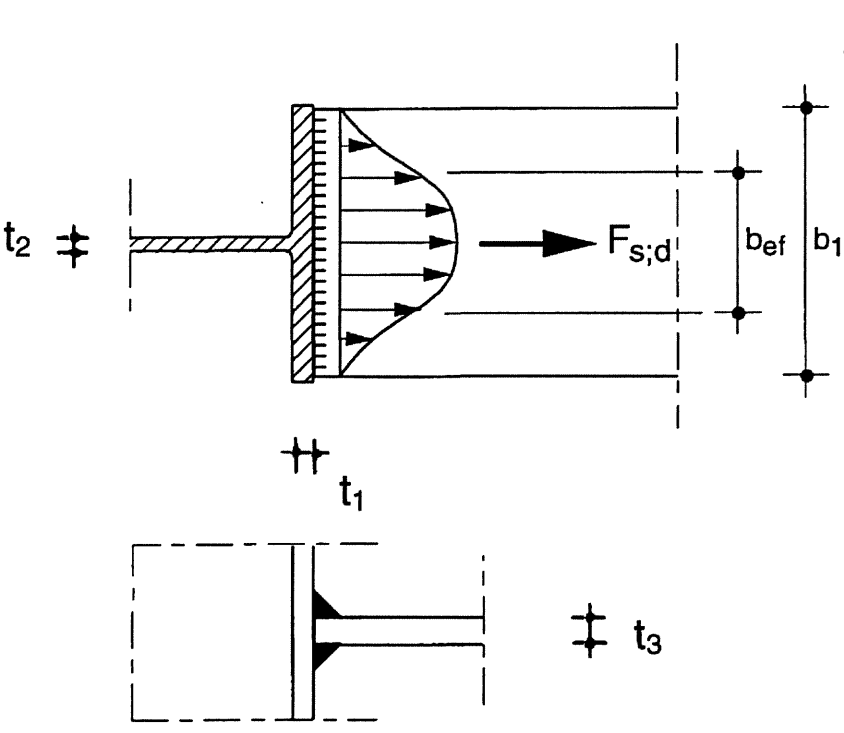
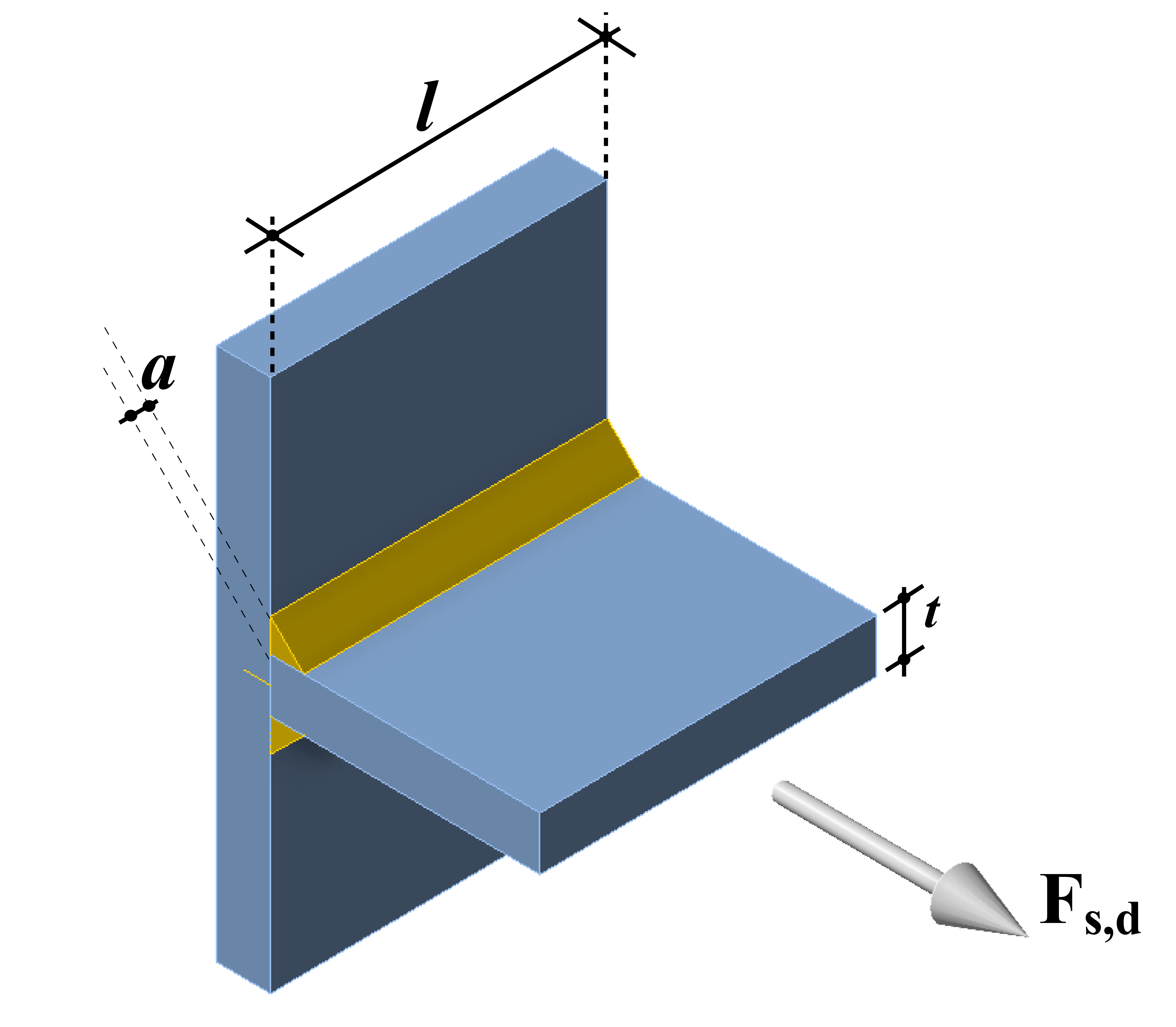
Uitgaande van het volgende basisgeval (Figuur 6):
Figuur 6 - Basisgeval plaat met normaalkracht loodrecht vast gelast op tweede plaat
Waarbij de grootte van Fs,d gekozen is als Fs,d = fy,plaat∙ t ∙ l, wordt voor dubbelzijdige hoeklassen de volgende formule afgeleid en gebruikt in de toetsing in IDEA:
Waarin:
| a | lasdikte |
| t | dikte van de aangesloten plaat |
| fy,plaat | representatieve waarde van de vloeigrens van de aangesloten plaat |
| fu,plaat | representatieve waarde van de treksterkte van de aangesloten plaat |
| fu,las | representatieve waarde van de breuksterkte van de las |
| βw | correlatiefactor afhankelijk van de treksterkte van het moedermateriaal |
| γM2 | partiële veiligheidsfactor voor bouten en lassen = 1,25 |
| γM0 | partiële veiligheidsfactor voor de weerstand van platen = 1,0 |
Dit leidt bij de volgende standaard staalsoorten tot de volgende minimum lasdikte-plaatdikte verhoudingen (Tabel 1).
Tabel 1 – Minimum lasdikte eis
| Staalkwaliteit | 1,1 ∙ fy,plaat/fu,plaat | Minimum lasdikte |
| S235 | 0,72 | a ≥ 0,33 ∙ t |
| S275 | 0,70 | a ≥ 0,34 ∙ t |
| S355 | 0,80 | a ≥ 0,46 ∙ t |
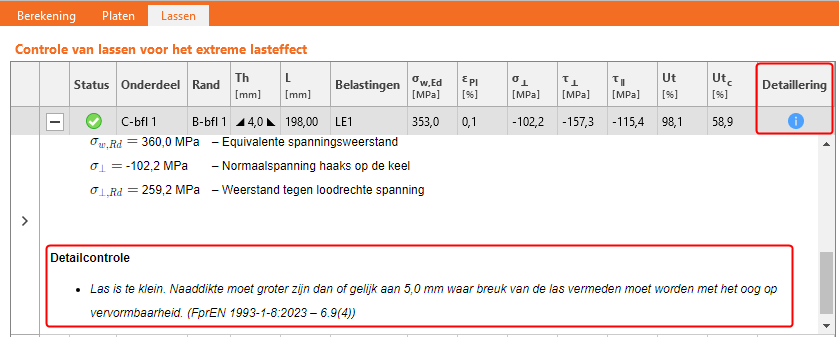
Voor enkelzijdige hoeklassen wordt de gevonden waarde met 2 vermenigvuldigd. De gebruiker van IDEA zal een waarschuwing krijgen als men niet voldoet aan deze minimale lasdikte eis voor ductiliteit (Figuur 7). Ook zal de gebruiker een foutmelding krijgen als lassen zijn toegepast met een keeldoorsnede kleiner dan 3,0 mm wat volgens EN 1993-1-8 art. 4.5.2(2) niet is toegestaan. Bovendien biedt het programma de mogelijkheid om de lasdikte van elke las in het model automatisch te bepalen door middel van de “Autodesign” functie.
Figuur 7 - Waarschuwing bij toepassing te kleine lasdikte in IDEA
Toch zijn er ook situaties denkbaar waarin men kan beargumenteren dat het niet nodig is om aan de minimale lasdikte eis voor ductiliteit te voldoen. Bijvoorbeeld bij lassen van een kolomvoetplaatverbinding die hoofdzakelijk op druk belast worden of als men kan aantonen dat er een ander onderdeel in de constructie aanwezig is dat sowieso eerder zou bezwijken met voldoende waarschuwend effect. Het programma moet hierbij altijd als een tool gezien worden, het is aan de ingenieur om op basis van zijn of haar engineering-judgement hier een goede afweging in te maken.