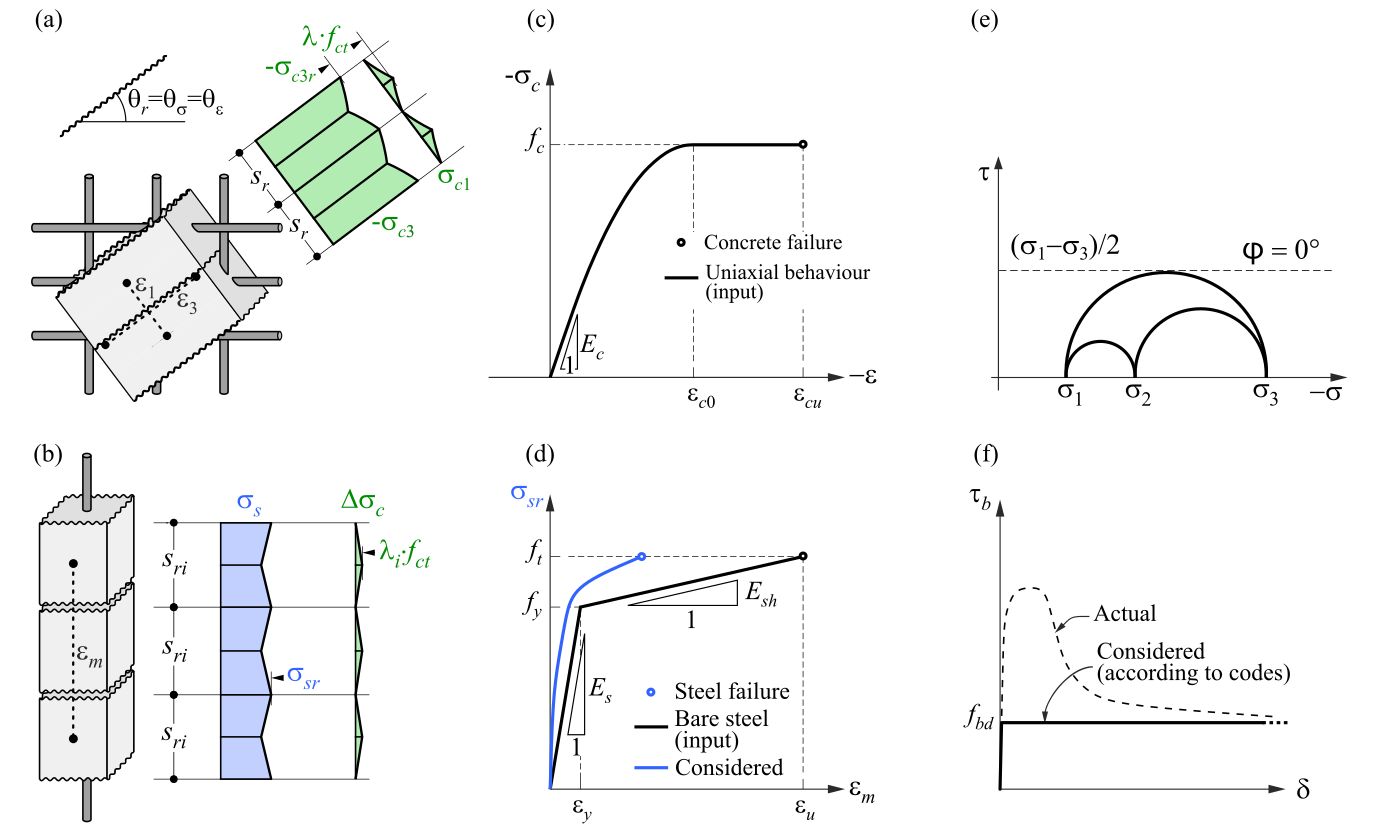
3D CSFM definieert het gedrag van beton op basis van de Mohr-Coulomb plasticiteitstheorie. De methode beschouwt de belangrijkste betonspanningen in druk en wapeningsspanningen (σsr) bij de scheuren terwijl de betontreksterkte wordt verwaarloosd, behalve voor het verstijvingseffect (tension stiffening) op de wapening.
σc1r, σc2r, σc3r ≤ 0 MPa
De wapeningsstaven zijn verbonden met betonnen eindige elementen door middel van Bond-elementen, waardoor slip tussen het beton en de wapening mogelijk is. Opgemerkt moet worden dat 3D CSFM niet geschikt is voor het simuleren van ongewapend beton vanwege de afwezigheid van treksterkte, wat kan resulteren in misleidende vervormingen en modelafwijkingen. In het algemeen bevat de Mohr-Coulomb theorie twee fundamentele eigenschappen die de ontwikkeling van het plasticiteitsoppervlak bij samendrukking en gedeeltelijk bij trek bepalen: de interne wrijvingshoek φ en de cohesieparameter c.
3D CSFM gaat uit van een interne wrijvingshoek van nul (fig. 1e), wat leidt tot een conservatief ontwerp omdat het plasticiteitsoppervlak lijkt op het Tresca model, dat onafhankelijk is van de eerste spanningsinvariant.
\( \textsf{\textit{\footnotesize{Fig. 1\qquad Basic assumptions of the 3D CSFM: (a) principal stresses in concrete; (b) stresses in the reinforcement direction;}}}\) \( \textsf{\textit{\footnotesize{(c) stress-strain diagram of concrete in terms of maximum stresses; (d) stress-strain diagram of reinforcement}}}\) \( \textsf{\textit{\footnotesize{in terms of stresses at cracks and average strains; (e) Mohr's circles for concrete model in 3D CSFM; (f) bond shear stress-slip}}}\) \( \textsf{\textit{\footnotesize{relationship for anchorage length verifications.}}}\)
Beton
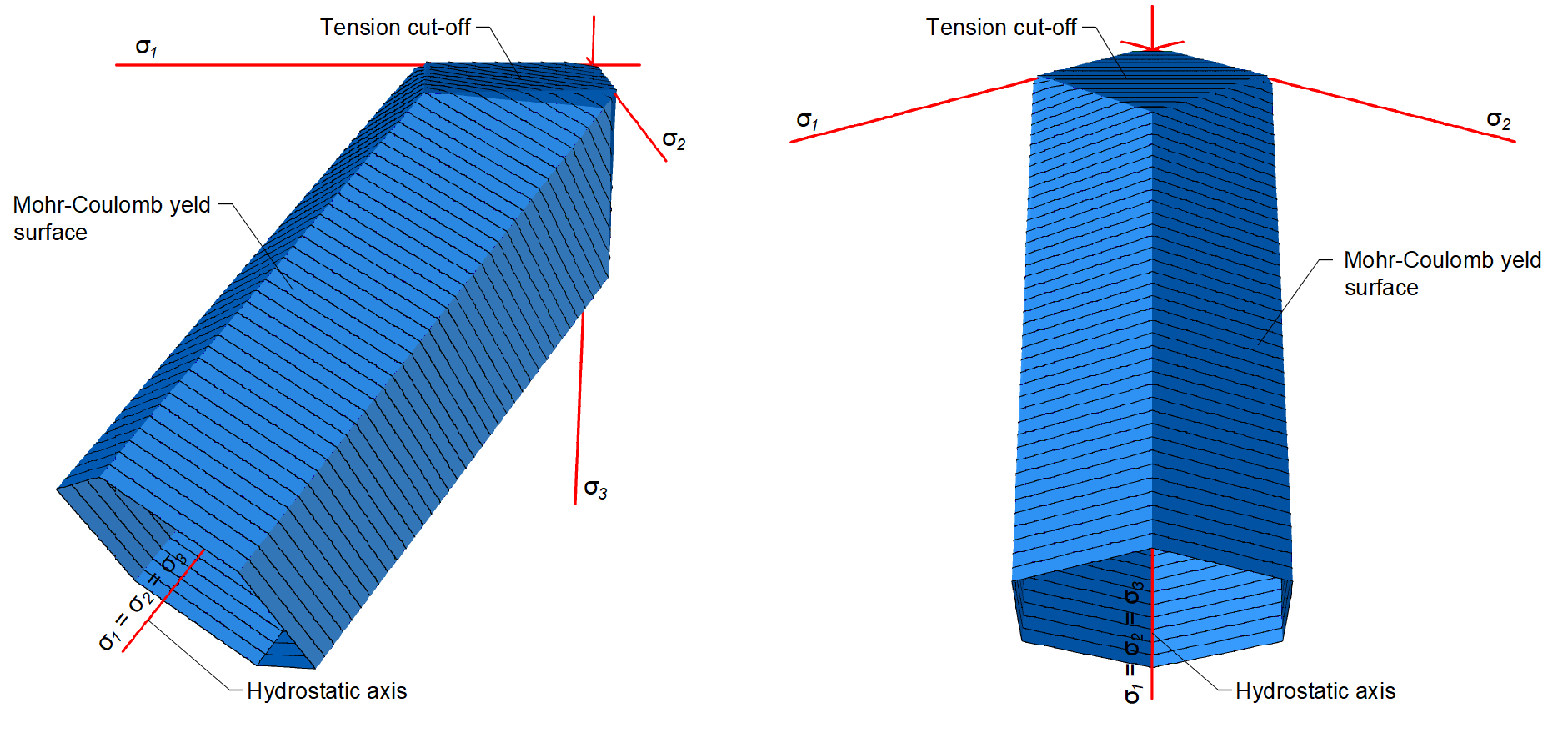
Het gepresenteerde materiaalmodel is een multisurface plasticiteitsmodel gegeven door de combinatie van het Mohr-Coloumb en Rankine model voor monotone belasting.
\[ \textsf{\textit{\footnotesize{Fig. 2\qquad Mohr-Coulomb multi-surface plasticity model for friction angle 0 degree}}}\]
Zoals reeds vermeld, is het materiaalmodel bedoeld voor gebruik in toepassingen die de respons van gewapend beton berekenen (niet geschikt voor gewoon beton). Dit komt door de uitsluiting van beton in trek. Daarom is het model niet geschikt voor constructie-elementen waar niet wordt voldaan aan de ontwerpregels voor gewapend beton, zoals minimale wapeningsverhouding, maximale staafafstand, enz. Het moet ook toegevoegd worden dat, omwille van de numerieke stabiliteit, een zeer kleine trekcapaciteit gedefinieerd is in het model. Het trekgedeelte wordt beperkt door vlakken die overeenkomen met het Rankine-model.
3D CSFM in IDEA StatiCa Detail beschouwt geen expliciet bezwijkcriterium in termen van rek voor beton in druk (d.w.z. het beschouwt een oneindig plastische tak nadat de piekspanning is bereikt). Door deze vereenvoudiging kan de vervormingscapaciteit van constructies die in druk bezwijken niet worden geverifieerd. Hun uiteindelijke capaciteit wordt echter goed voorspeld als de toename van de brosheid van beton naarmate de materiaalsterkte toeneemt, in aanmerking wordt genomen door middel van de reductiefactor die als volgt is gedefinieerd in de Model Code 2010:
\[f_{c,red} = \eta _{fc} \cdot f_{c}\]
\[{\eta _{fc}} = {\left( {\frac{{30}}{{{f_{c}}}}} \right)^{\frac{1}{3}}} \le 1\]
waarbij:
fc de karakteristieke sterkte van beton is (in MPa voor de definitie van \( \eta_{fc} \)).
De fc,red wordt dan vergeleken met de equivalente hoofdspanning σc,eq in beton, die verder zal worden gedefinieerd, uiteraard met inachtneming van alle veiligheidsfactoren die door de code worden voorgeschreven.
Een gedetailleerde beschrijving van het betonmodel is te vinden via de volgende link:
Wapening
Het bilineaire spanning-rekdiagram voor wapeningsstaven, zoals gedefinieerd door ontwerpnormen (Fig. 1d), vertegenwoordigt een geïdealiseerd model. Dit model vereist kennis van de basiseigenschappen van de wapening tijdens de ontwerpfase, in het bijzonder de sterkte- en ductiliteitsklasse. Als alternatief hebben gebruikers de optie om een aangepaste spanning-rek relatie te definiëren.
Spanningsverstijving wordt beschouwd door de spanning-rek relatie van de kale wapeningsstaaf te wijzigen om de gemiddelde stijfheid van de staven in het beton (εm) weer te geven (Fig 1b).
Verankering
Slip tussen wapening en beton wordt geïntroduceerd in het eindige-elementenmodel door de vereenvoudigde plastische relatie te beschouwen zoals voorgesteld in (Fig. 1f), waarbij fbd de ontwerpwaarde is (gefactoriseerde waarde) van de uiteindelijke aanhechtingsspanning gespecificeerd door de ontwerpcode voor de specifieke aanhechtingsomstandigheden (bond conditions).
Dit is een vereenvoudigd model met als enig doel het verifiëren van aanhechtingsvoorschriften volgens ontwerpnormen (d.w.z. verankering van wapening). De vermindering van de verankeringslengte bij het gebruik van haken, lussen en gelijkaardige staafvormen kan overwogen worden door een bepaalde capaciteit te definiëren aan het uiteinde van de wapening, zoals verder beschreven zal worden.
Ankers
Het element van het anker is gedefinieerd als zijnde in staat om normale trek- of drukkrachten over te brengen evenals afschuifkrachten waarbij ook de buigstijfheid in beschouwing wordt genomen. Echter, alleen de normaalspanning in de ankers wordt geëvalueerd.
Er zijn twee typen ankers beschikbaar:
- Chemische verankering (lijmanker) - Achteraf geplaatst
- In het werk gestorte ankers - Vooraf geplaatst
Het gedrag van vooraf geplaatste wapening is hetzelfde als dat van klassieke wapening (Ankertype, aanhechting, etc.) Voor lijmankers is het mogelijk om de ontwerpwaarde voor de aanhechtsterkte (Bond strength) direct te definiëren. Deze waarde moet worden afgelezen van de technische documenten van de fabrikant.