As described in Internal forces in the chapter Transformation of recalculated internal forces to the centroid of cross-section, surface dimensioning forces are transformed to the centroid of a 2D element cross-section. The result of this transformation is a bending moment and a normal force, acting in the centroid of a rectangular cross-section, in which the edge length is 1 m and height corresponds to the thickness of the slab.
The checks of the 2D element are performed in all defined directions at once. The program automatically converts the reinforcement to the check direction using the formula:
\[{{A}_{Si,\alpha }}={{A}_{S}}\cdot {{\cos }^{2}}({{\alpha }_{i}})\]
| Description | |
| Asi,a | The area of the ith reinforcement layer recalculated to the direction a |
| As | The area of the ith reinforcement layer of the 2D element |
| αi | The angle between ith reinforcement layer and the check direction |
| Remark: |
| Distribution reinforcement in 2D elements of type slab and shell-slab is taken into account only in the detailing provision check, it is not used in other 2D element checks. |
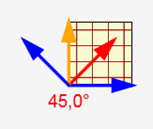
Results of checks in defined directions
All enabled checks are performed in all required directions automatically. The presentation of results is similar to the presentation of 1D element results. The presentation for 2D elements enables to set the direction to be presented. Results for 2D elements are presented in check directions. All directions, in which the checks were calculated, are drawn in graphical presentation.
The arrows in the picture represent check directions, where the orange is the direction of the maximum check value and the red is the current check direction. To change the current direction click the arrow or click the appropriate button in the ribbon.
| Remark: |
| After the calculation finishes, the check directions in all checks are set to the direction of maximum cross-section utilization. |
Results in particular checks are presented in the current direction. The angle of the check is displayed above the table with the check summary.
The results in the extreme direction are printed in the report.
Ultimate limit state
The principles of ULS checks are described in the theoretical background manual for 1D elements. Only the differences for 2D elements are described in the following chapters.
Capacity check
The capacity check does not differ from the 1D elements checks. The load acts only in one plane, thus the check type is N + M.
Response check
The response checks for particular check directions use the same algorithms as checks of 1D elements.
Interaction check
Unlike for 1D elements, the interaction check is performed only to evaluate the exploitation V + M, the interaction of shear and bending moment. Values VRd,c and VRd,max can be verified in the summary table of the interaction check.
Capacity check comparison between IDEA Concrete, RFEM, and SCIA Engineer
To compare the capacity check results with RFEM and SCIA Engineer the same data as described in Internal forces in the chapter Comparison of internal forces calculation with programs RFEM and SCIA Engineer were used. The comparison was done in two points of the slab.
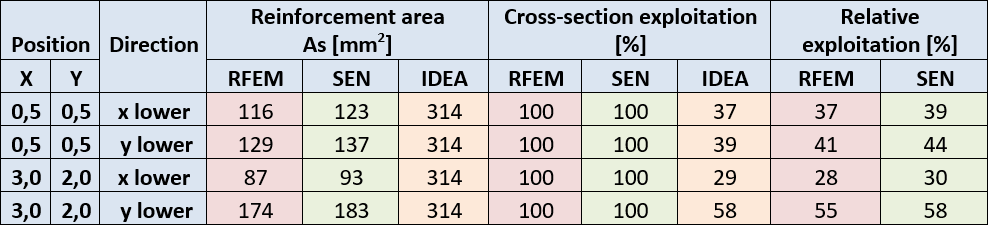
Because programs RFEM and SEN do not check the real reinforcement in the slab, but only design the necessary reinforcement area, two methods were used to compare the calculation. The first one compares the exploitation of cross-section for required reinforcement designed in RFEM and SEN, assuming that the cross-section is exploited to 100% just when using the calculated required area of reinforcement.
The exploitation of cross-section reinforced in IDEA concrete can be expressed relatively then.
Relative exploitation = As, req / As, RCS × 100 [%]
| Description | |
| As, req | Required reinforcement area calculated in RFEM or SEN |
| As, RCS | Area of reinforcement in IDEA Concrete |
| 100 [%] | Percentage |
The cross-section in IDEA Concrete was reinforced at the lower surface using reinforcement d=10 mm in 200 mm distances in both directions, the area of reinforcement in both directions is 314 mm2.
The table shows good compliance with exploitation for all programs.
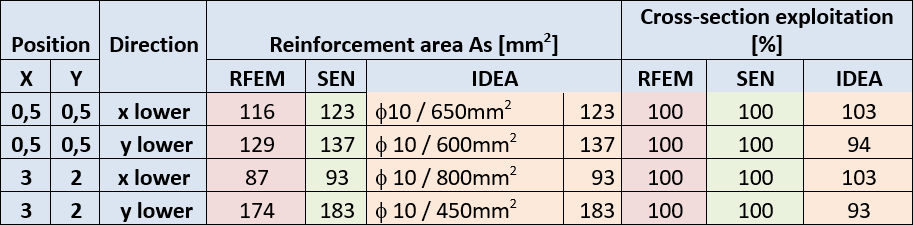
Reinforcement with approximately same area was defined in IDEA Concrete as the calculated required reinforcement in RFEM and SEN for the second method. Afterwards, the exploitation of the cross-section was compared. Results are displayed in the following table:
The good compliance of results is here too.
Serviceability limit state
Stress limitation
Check of stress limitation does not differ from checks for 1D elements.
Crack width check
In advance, 1D elements check the direction of the crack that can be drawn for 2D elements.
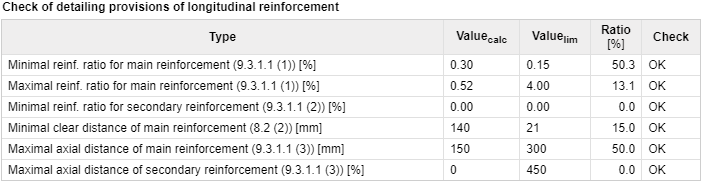
Detailing provisions
Detailing provisions check of 2D elements can be split into two basic groups:
- Reinforcement percentage check
- Bar distances check
The detailing provisions check depends on the type of 2D element too. The separate checks for the main and for distribution reinforcement are performed for shell-slab and slab elements. The vertical and horizontal reinforcement is distinguished for wall elements.
The reinforcement percentage check is performed in the direction of principal stresses. The reinforcement defined in the cutting of 2D element (except the distribution reinforcement) is transformed to the principal stresses directions.
The bars distance check is performed perpendicular to the direction of the defined reinforcement. This check is performed for all defined reinforcement layers and the limit values depend on the type of checked element and on the type of defined reinforcement.