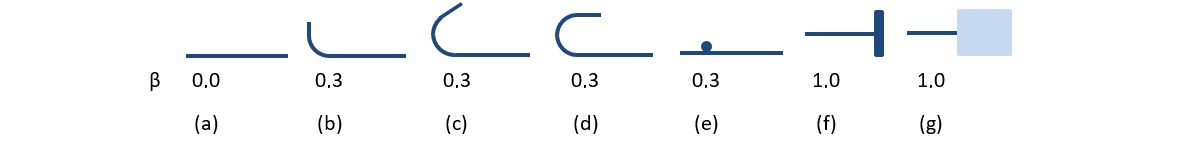IDEA StatiCa Detail - Constructief ontwerp van betonnen 3D discontinuïteiten
Constructief ontwerp van betonnen 3D discontinuïteiten in IDEA StatiCa Detail
Inleiding tot de 3D CSFM-methode
Algemene inleiding voor het constructief ontwerp van betonnen 3D details
Belangrijkste aannames en beperkingen
Mohr-Coulomb plasticiteitstheorie implementatie in 3D CSFM
Algemene mechanica aannames voor 3D CSFM
Analysemodel van IDEA StatiCa 3D Detail
Inleiding tot eindige-elementenimplementatie
Oplossingsmethode en belastingscontrolealgoritme voor 3D CSFM
Model geïmporteerd uit IDEA StatiCa Connection
Model verificatie
Constructieve controles volgens Eurocode
Gedeeltelijke veiligheidsfactoren
Uiteindelijke grenstoestandscontroles
Inleiding tot de 3D CSFM methode
Theoretische achtergrond 3D Detail - Algemene intoductie
In de praktijk kunnen ingenieurs verschillende soorten eindige elementen tegenkomen, variërend van eenvoudige 1D staafelementen tot complexe 3D solid-elementen, die worden gebruikt voor de analyse en het ontwerp van constructieve elementen in uiteenlopende toepassingen. Een gemeenschappelijk kenmerk van de meeste berekeningen in de praktijk is het lineaire gedrag van de modellen. Dit biedt onmiskenbare voordelen, zoals snelheid, helderheid en het feit dat deze aanpak voor een breed scala aan problemen vaak meer dan voldoende is.
In de wereld van betonconstructies blijkt echter regelmatig dat een lineaire benadering niet volstaat. Zodra de eerste scheuren in een belaste constructie optreden, worden spanningen herverdeeld en wordt het probleem significant niet-lineair.
In dergelijke gevallen is het noodzakelijk om een geavanceerdere benadering te kiezen. Voor 1D-gebaseerde analyses zijn vaak analytische methoden beschikbaar die direct in de normen zijn opgenomen. Bekende modellen zoals Strut-and-Tie kunnen worden toegepast voor 2D-vlakke elementen en discontinuïteitsgebieden (D-gebieden). Voor meer geavanceerde analyses kan de spanningsveldmethode (CSFM), zoals geïmplementeerd in IDEA StatiCa Detail, worden gebruikt.
Wanneer een probleem echter niet vereenvoudigd kan worden tot vlak gedrag, zijn de beschikbare opties beperkt. Een ingenieur kan bijvoorbeeld een 3D Strut-and-Tie-model ontwikkelen of semi-wetenschappelijke software gebruiken voor een nauwkeurige analyse. Deze methoden zijn echter vaak tijdrovend, niet normconform en vereisen specialistische kennis van geavanceerde modelleertechnieken.
Om deze uitdaging aan te gaan, heeft IDEA StatiCa de 3D CSFM (Compatible Stress Field Method) ontwikkeld en geïmplementeerd in de Detail-applicatie. 3D CSFM breidt de gevestigde CSFM uit naar een derde dimensie en biedt een snelle, normconforme oplossing die toegankelijk is voor de alledaagse ingenieur. Hiermee ontstaat een unieke mogelijkheid om de complexe details van betonconstructies veilig en efficiënt te analyseren.
Belangrijkste aannames en beperkingen
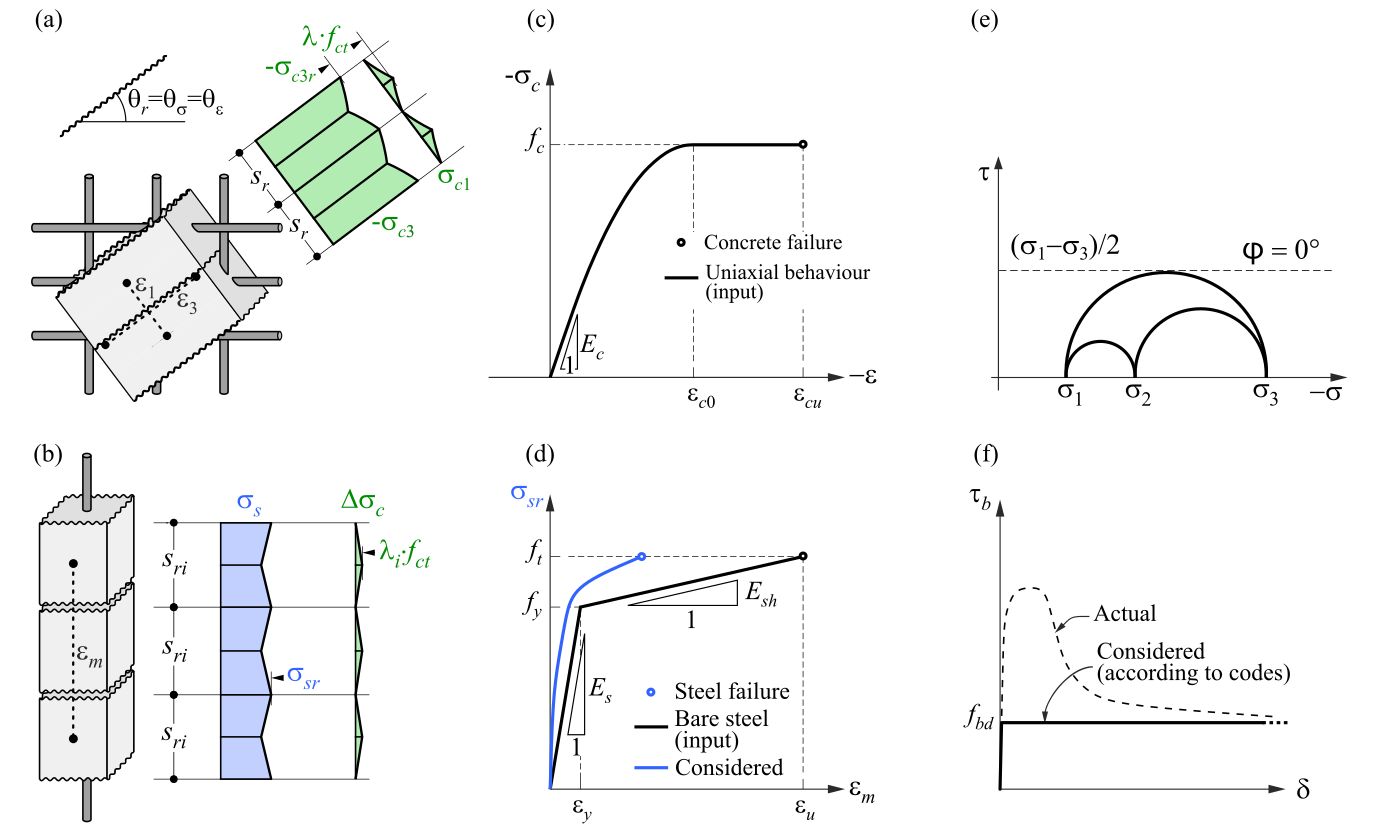
3D CSFM definieert het gedrag van beton op basis van de Mohr-Coulomb plasticiteitstheorie. De methode beschouwt de belangrijkste betonspanningen in druk en wapeningsspanningen (σsr) bij de scheuren terwijl de betontreksterkte wordt verwaarloosd, behalve voor het verstijvingseffect (tension stiffening) op de wapening.
σc1r, σc2r, σc3r ≤ 0 MPa
De wapeningsstaven zijn verbonden met betonnen eindige elementen door middel van Bond-elementen, waardoor slip tussen het beton en de wapening mogelijk is. Opgemerkt moet worden dat 3D CSFM niet geschikt is voor het simuleren van ongewapend beton vanwege de afwezigheid van treksterkte, wat kan resulteren in misleidende vervormingen en modelafwijkingen. In het algemeen bevat de Mohr-Coulomb theorie twee fundamentele eigenschappen die de ontwikkeling van het plasticiteitsoppervlak bij samendrukking en gedeeltelijk bij trek bepalen: de interne wrijvingshoek φ en de cohesieparameter c.
3D CSFM gaat uit van een interne wrijvingshoek van nul (fig. 1e), wat leidt tot een conservatief ontwerp omdat het plasticiteitsoppervlak lijkt op het Tresca model, dat onafhankelijk is van de eerste spanningsinvariant.
\( \textsf{\textit{\footnotesize{Fig. 1\qquad Basic assumptions of the 3D CSFM: (a) principal stresses in concrete; (b) stresses in the reinforcement direction;}}}\) \( \textsf{\textit{\footnotesize{(c) stress-strain diagram of concrete in terms of maximum stresses; (d) stress-strain diagram of reinforcement}}}\) \( \textsf{\textit{\footnotesize{in terms of stresses at cracks and average strains; (e) Mohr's circles for concrete model in 3D CSFM; (f) bond shear stress-slip}}}\) \( \textsf{\textit{\footnotesize{relationship for anchorage length verifications.}}}\)
Beton
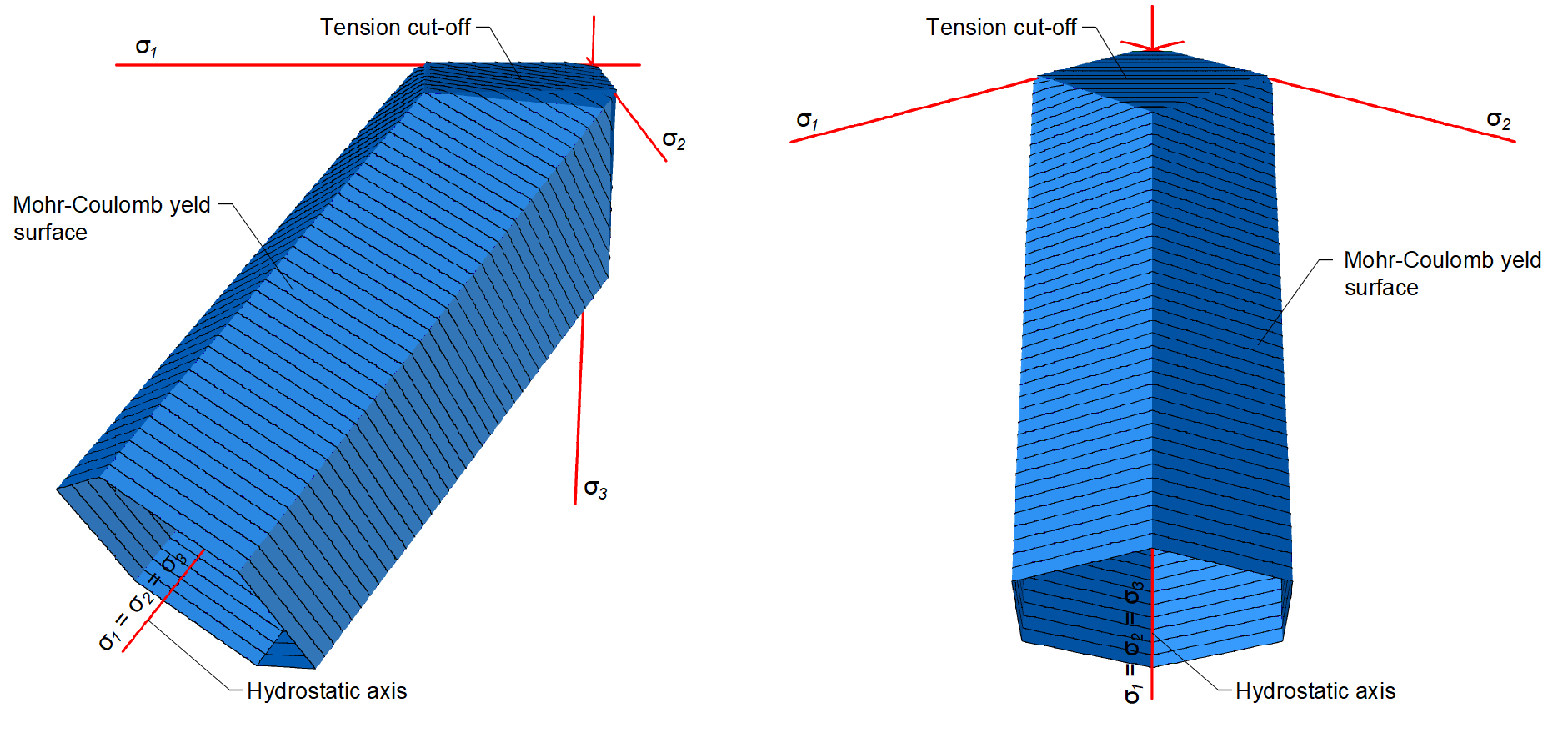
Het gepresenteerde materiaalmodel is een multisurface plasticiteitsmodel gegeven door de combinatie van het Mohr-Coloumb en Rankine model voor monotone belasting.
\[ \textsf{\textit{\footnotesize{Fig. 2\qquad Mohr-Coulomb multi-surface plasticity model for friction angle 0 degree}}}\]
Zoals reeds vermeld, is het materiaalmodel bedoeld voor gebruik in toepassingen die de respons van gewapend beton berekenen (niet geschikt voor gewoon beton). Dit komt door de uitsluiting van beton in trek. Daarom is het model niet geschikt voor constructie-elementen waar niet wordt voldaan aan de ontwerpregels voor gewapend beton, zoals minimale wapeningsverhouding, maximale staafafstand, enz. Het moet ook toegevoegd worden dat, omwille van de numerieke stabiliteit, een zeer kleine trekcapaciteit gedefinieerd is in het model. Het trekgedeelte wordt beperkt door vlakken die overeenkomen met het Rankine-model.
3D CSFM in IDEA StatiCa Detail beschouwt geen expliciet bezwijkcriterium in termen van rek voor beton in druk (d.w.z. het beschouwt een oneindig plastische tak nadat de piekspanning is bereikt). Door deze vereenvoudiging kan de vervormingscapaciteit van constructies die in druk bezwijken niet worden geverifieerd. Hun uiteindelijke capaciteit wordt echter goed voorspeld als de toename van de brosheid van beton naarmate de materiaalsterkte toeneemt, in aanmerking wordt genomen door middel van de reductiefactor die als volgt is gedefinieerd in de Model Code 2010:
\[f_{c,red} = \eta _{fc} \cdot f_{c}\]
\[{\eta _{fc}} = {\left( {\frac{{30}}{{{f_{c}}}}} \right)^{\frac{1}{3}}} \le 1\]
waarbij:
fc de karakteristieke sterkte van beton is (in MPa voor de definitie van \( \eta_{fc} \)).
De fc,red wordt dan vergeleken met de equivalente hoofdspanning σc,eq in beton, die verder zal worden gedefinieerd, uiteraard met inachtneming van alle veiligheidsfactoren die door de code worden voorgeschreven.
Een gedetailleerde beschrijving van het betonmodel is te vinden via de volgende link:
Wapening
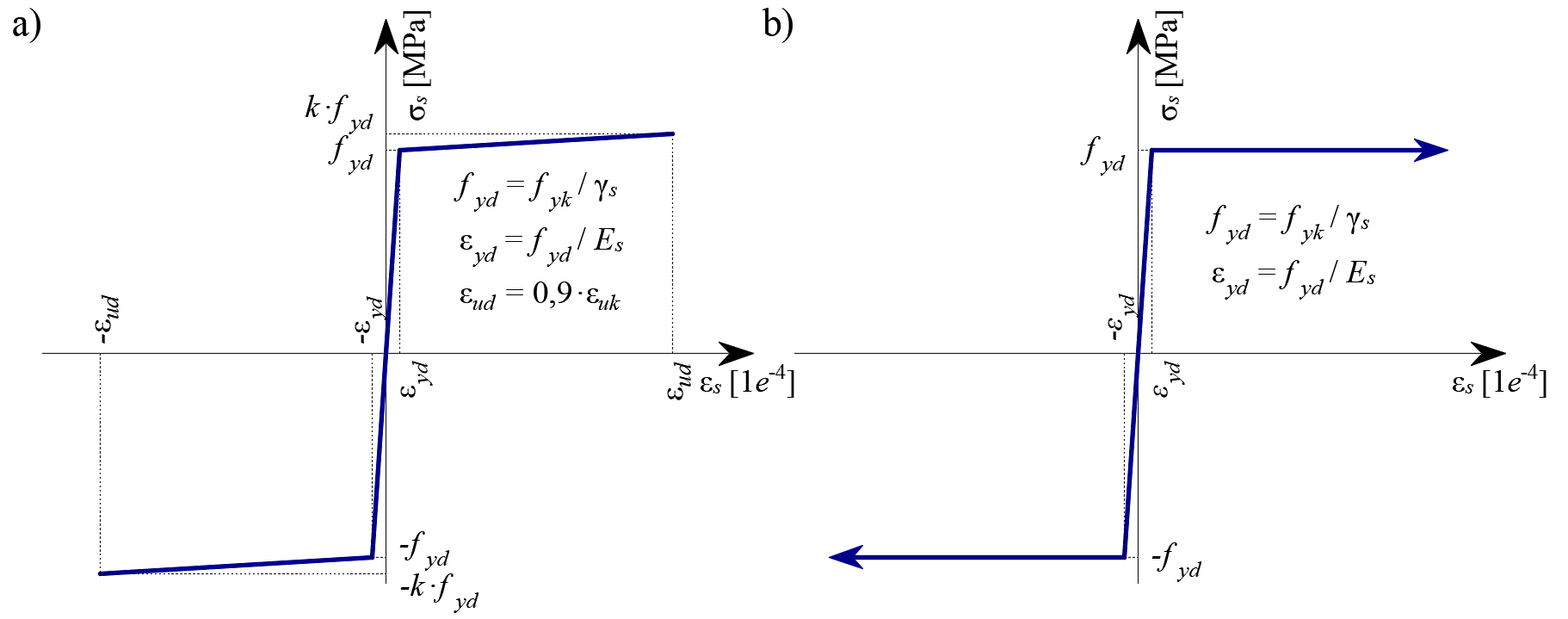
Het bilineaire spanning-rekdiagram voor wapeningsstaven, zoals gedefinieerd door ontwerpnormen (Fig. 1d), vertegenwoordigt een geïdealiseerd model. Dit model vereist kennis van de basiseigenschappen van de wapening tijdens de ontwerpfase, in het bijzonder de sterkte- en ductiliteitsklasse. Als alternatief hebben gebruikers de optie om een aangepaste spanning-rek relatie te definiëren.
Spanningsverstijving wordt beschouwd door de spanning-rek relatie van de kale wapeningsstaaf te wijzigen om de gemiddelde stijfheid van de staven in het beton (εm) weer te geven (Fig 1b).
Verankering
Slip tussen wapening en beton wordt geïntroduceerd in het eindige-elementenmodel door de vereenvoudigde plastische relatie te beschouwen zoals voorgesteld in (Fig. 1f), waarbij fbd de ontwerpwaarde is (gefactoriseerde waarde) van de uiteindelijke aanhechtingsspanning gespecificeerd door de ontwerpcode voor de specifieke aanhechtingsomstandigheden (bond conditions).
Dit is een vereenvoudigd model met als enig doel het verifiëren van aanhechtingsvoorschriften volgens ontwerpnormen (d.w.z. verankering van wapening). De vermindering van de verankeringslengte bij het gebruik van haken, lussen en gelijkaardige staafvormen kan overwogen worden door een bepaalde capaciteit te definiëren aan het uiteinde van de wapening, zoals verder beschreven zal worden.
Ankers
Het element van het anker is gedefinieerd als zijnde in staat om normale trek- of drukkrachten over te brengen evenals afschuifkrachten waarbij ook de buigstijfheid in beschouwing wordt genomen. Echter, alleen de normaalspanning in de ankers wordt geëvalueerd.
Er zijn twee typen ankers beschikbaar:
- Chemische verankering (lijmanker) - Achteraf geplaatst
- In het werk gestorte ankers - Vooraf geplaatst
Het gedrag van vooraf geplaatste wapening is hetzelfde als dat van klassieke wapening (Ankertype, aanhechting, etc.) Voor lijmankers is het mogelijk om de ontwerpwaarde voor de aanhechtsterkte (Bond strength) direct te definiëren. Deze waarde moet worden afgelezen van de technische documenten van de fabrikant.
Implementatie van Mohr-Coulomb plasticiteitstheorie in 3D CSFM
In het volgende hoofdstuk bekijken we hoe de Mohr-Coulomb theorie is geïmplementeerd in 3D CSFM. We zullen uitleggen hoe het samendrukkingseffect (confinement effect) in triaxiale spanning wordt beschouwd en hoe de equivalente hoofdspanning σc,eq wordt berekend, die wordt gebruikt om de capaciteit van het beton te bepalen.
Inleiding tot de theorie
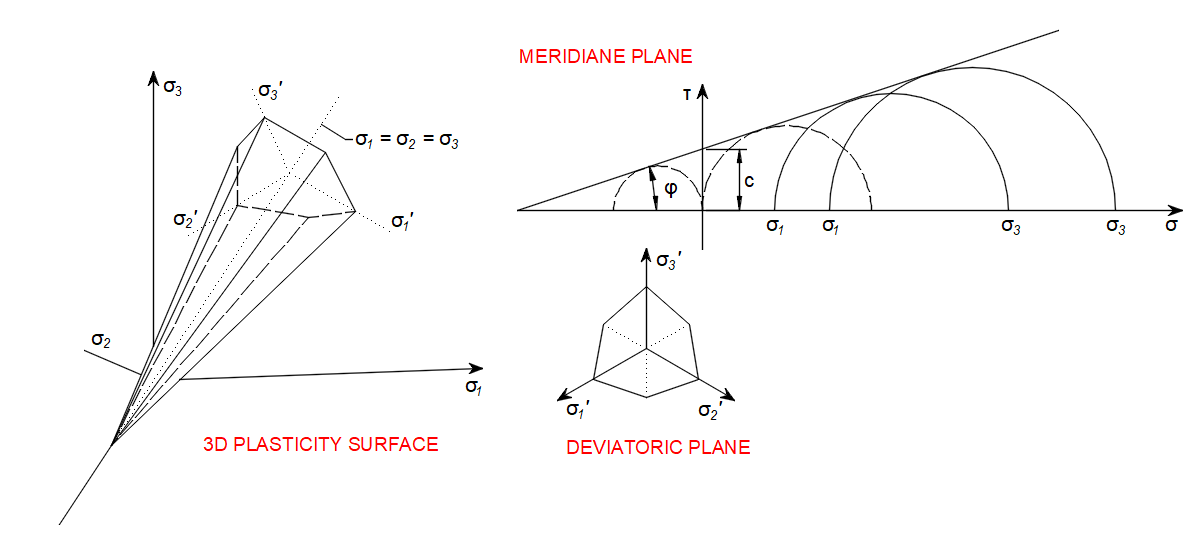
De Mohr-Coulomb theorie is een wiskundig model dat de reactie van brosse materialen op afschuif- en normaalspanning beschrijft. De meeste klassieke technische materialen volgen deze regel bij afschuiving. Over het algemeen is de theorie van toepassing op materialen waarvan de druksterkte veel groter is dan de treksterkte.
\[ \textsf{\textit{\footnotesize{Fig. 3\qquad Mohr-Coulomb Plasticity Model }}}\]
In de bouwkunde wordt het gebruikt om de bezwijkbelasting en de breukhoek te bepalen voor de verplaatsing van het breukvlak in beton en soortgelijke materialen. De wrijvingshypothese (Coulomb's friction hypothesis) wordt gebruikt om de combinatie van schuifspanning en normaalspanning te bepalen die een breuklijn zal veroorzaken. De cirkel van Mohr wordt gebruikt om te bepalen welke hoofdspanningen deze combinatie van schuifspanning en normaalspanning zullen veroorzaken en de hoek van het vlak waarin dit zal gebeuren. Volgens het normaliteitsprincipe zal de spanning bij breuk loodrecht staan op de lijn die de breektoestand beschrijft.
\[ \textsf{\textit{\footnotesize{Fig. 4\qquad Meridian plane and tension cut-off}}}\]
Er kan worden aangetoond dat bij een materiaal dat bezwijkt volgens de wrijvingshypothese van Coulomb de verplaatsing bij bezwijken een hoek vormt met de breuklijn gelijk aan de wrijvingshoek. Dit maakt de sterkte van het materiaal bepaalbaar door de uitwendige mechanische arbeid geïntroduceerd door de verplaatsing en de uitwendige belasting te vergelijken met de inwendige mechanische arbeid geïntroduceerd door de rek en spanning op de breuklijn. Door behoud van energie moet de som hiervan nul zijn en dit maakt het mogelijk om de bezwijkkracht van de constructie te berekenen.
Implementatie in 3D CSFM
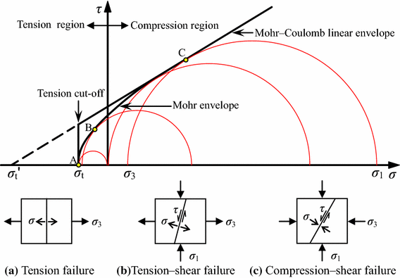
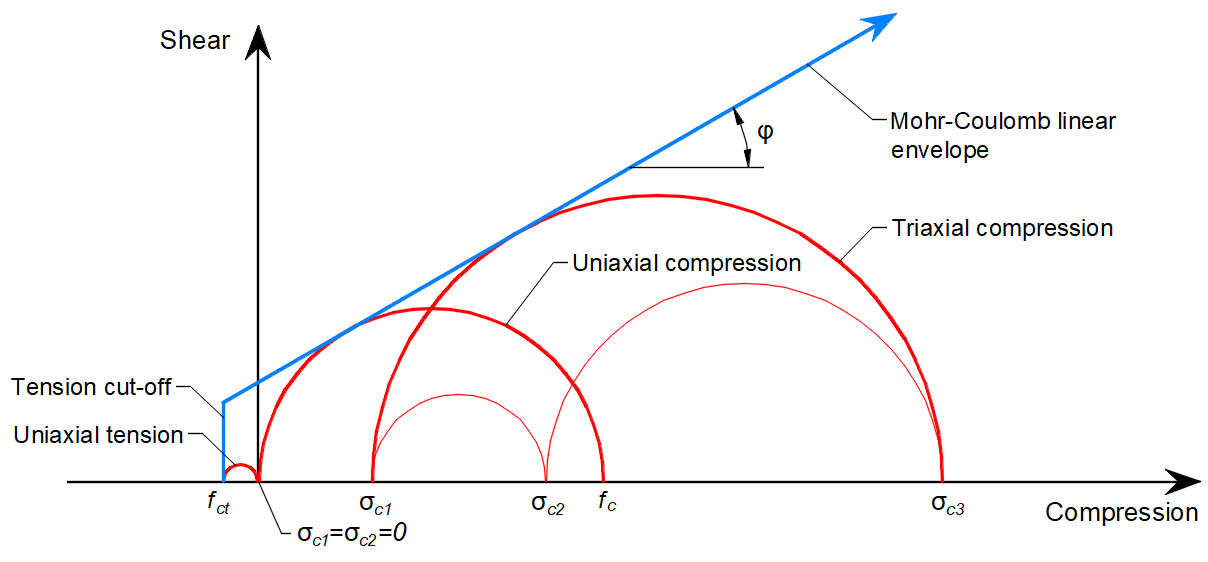
In het algemeen kunnen voor een gegeven hoek van inwendige wrijving van het beton, die rond φ = 30-40° ligt in referentie [1], [2], [3], [4], de trek- en druksterkte van het beton Mohr's cirkels worden geconstrueerd zoals in afbeelding 5.
\[ \textsf{\textit{\footnotesize{Fig. 5\qquad Mohr's circles for concrete}}}\]
Waarbij fc de betonsterkte in druk is, fct de betonsterkte in trek, φ de hoek van interne wrijving en σc1, σc3 de hoofdspanningen van beton onder triaxiale druk.
Het valt op dat als de hoofdspanning σc3 toeneemt, het maximaal mogelijke verschil tussen de waarden van σc3 en σc1, die we definiëren als maximaal σc,eq (zie hieronder), ook toeneemt. Dit verschil komt overeen met tweemaal de deviatorische spanning die in de literatuur gedefinieerd is als een straal van de mohr cirkels.
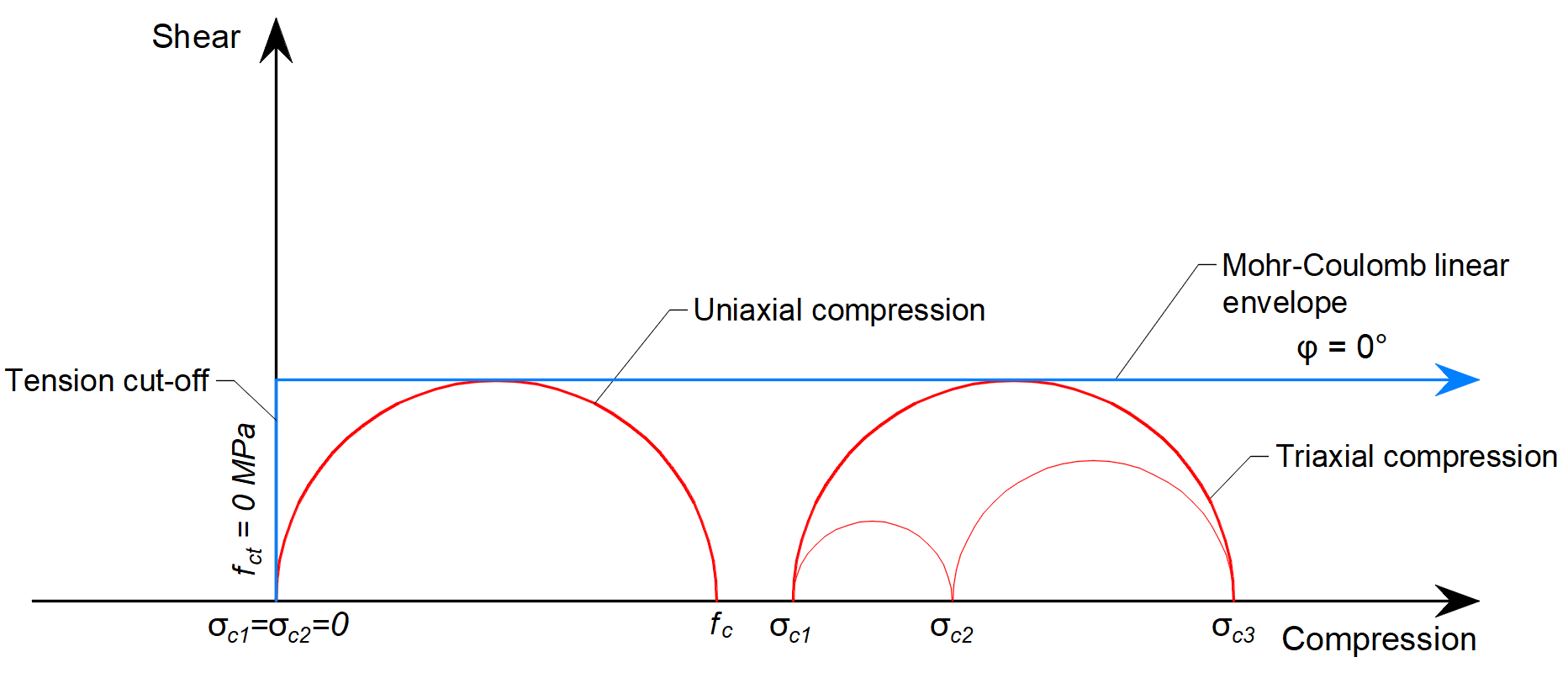
In 3D CSFM geïmplementeerd in IDEA StatiCa Detail, wordt de hoek van interne wrijving beschouwd als φ = 0°, zoals getoond in Figuur 6.
\[ \textsf{\textit{\footnotesize{Fig. 6\qquad Mohr's circles for concrete implemented in IDEA StatiCa Detail}}}\]
Het praktische gevolg van deze implementatie is dat het maximale verschil tussen σc3 en σc1 constant is als σc3 toeneemt.
Equivalente hoofdspanning drukt de equivalente uni-axiale spanning uit voor een algemene tri-axiale spanningstoestand.
\[\sigma_{c,eq} = \sigma_{c3} - \sigma_{c1}\]
De σc,eq waarde kan daarom direct vergeleken worden met uniaxiale sterktelimieten.
\[\frac{\sigma_{c,eq} }{ \sigma_{c,lim}} \le 1\]
Waarbij σc,lim de ontwerp (gefactoriseerde) uni-axiale sterkte van beton fc is.
Als we Figuur 5, waarin de werkelijke hoek van inwendige wrijving wordt gebruikt, vergelijken met Figuur 6, waarin de Mohr-Coulomb theorie wordt toegepast met een hoek van inwendige wrijving van nul, kunnen we zien dat de benadering die is gekozen voor de berekeningen in Detail zeer conservatief is voor de beoordeling van de triaxiale spanningstoestand.
Voor een beter begrip van de gebieden die beïnvloed worden door tri-axiale drukspanning, is de uitdrukking van de toename van de effectieve materiaalsterkte door tri-axiale druk toegevoegd aan de IDEA StatiCa Detail toepassing als een verhouding σc3/σc,lim. Je kunt deze verhouding vinden onder de Sterkte controle.
In de aanvullende resultaten kan de gebruiker ook de κ factor vinden, die de tri-axialiteit op een andere manier verklaart.
\[\kappa = \frac{ \sigma_{c3}}{ \sigma_{c,eq}}\]
De betonsterktecontrole kan dan worden herschreven als:
\[\frac{\sigma_{c,eq} }{ \sigma_{c,lim}} = \frac{\sigma_{c,3} }{ \kappa \cdot \sigma_{c,lim}} \le 1\]
Uit het voorgaande volgt dat als het element onder hydrostatische spanning staat - σc3=σc2=σc1, de equivalente hoofdspanning σc,eq de nulwaarde zal hebben en de kappa factor oneindig zal worden.
Meer hierover kan hier gevonden worden: Tri-axiale spanning - het Confinement effect
Algemene aannames voor 3D CSFM
Evenwichtsvergelijkingen
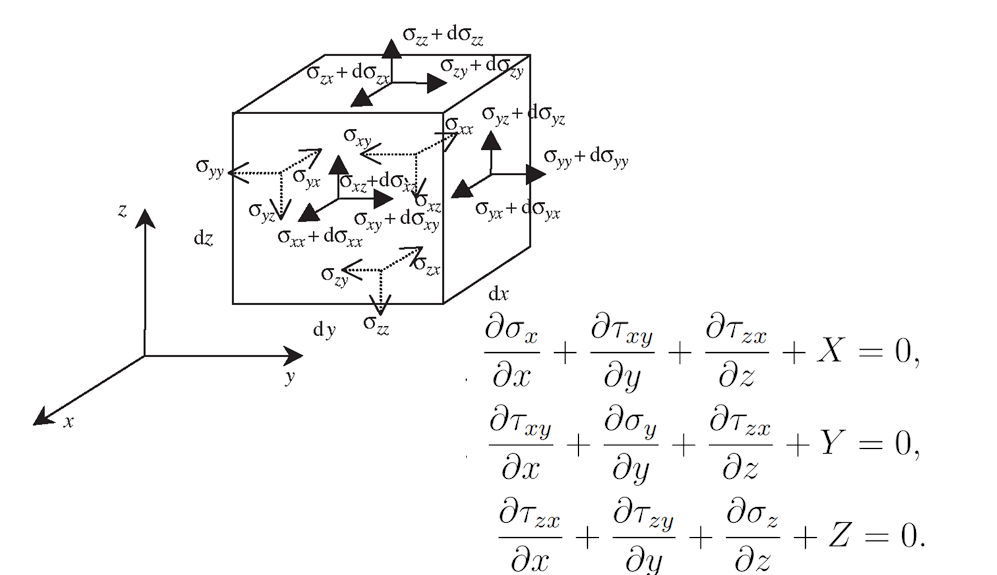
De theorie van kleine vervormingen maakt het mogelijk om de evenwichtsvergelijking op te stellen op basis van het onvervormde volume met behulp van een eerste-orde benadering.
\[ \textsf{\textit{\footnotesize{Fig. 7\qquad Equilibrium equations and graphical representation on infinitesimal element}}}\]
Compatibiliteitsvergelijkingen
Een vast lichaam bestaat uit infinitesimale volumes of materiaalpunten, die elk onderling verbonden zijn zonder openingen of overlappingen. Er moet aan wiskundige voorwaarden worden voldaan om het optreden van spleten of overlappingen te voorkomen wanneer een continuümlichaam vervorming ondergaat.
Spanningsvergelijkingen
De vergelijkingen die het gedrag van 3D-elementen bepalen, spelen een centrale rol in de analyse van materiaalgedrag in constructiemechanica. Deze vergelijkingen zijn geformuleerd om het niet-lineaire isotrope gedrag, dat geldig is voor massieve blokelementen in IDEA StatiCa Detail, te accommoderen.
Bij een 3D-wand is het essentieel om rekening te houden met orthotroop gedrag over de dikte, met speciale aandacht voor de spanning in het beton door de afwezigheid van dwarswapening. De orthotropie wordt veroorzaakt door het toestaan van de spanning in het beton in een uitwendige richting.
\[ \textsf{\textit{\footnotesize{Fig. 8\qquad Linearly elastic isotropic compliance matrix}}}\]
Analysemodel van IDEA StatiCa 3D Detail
Een inleiding tot eindige elementen implementatie
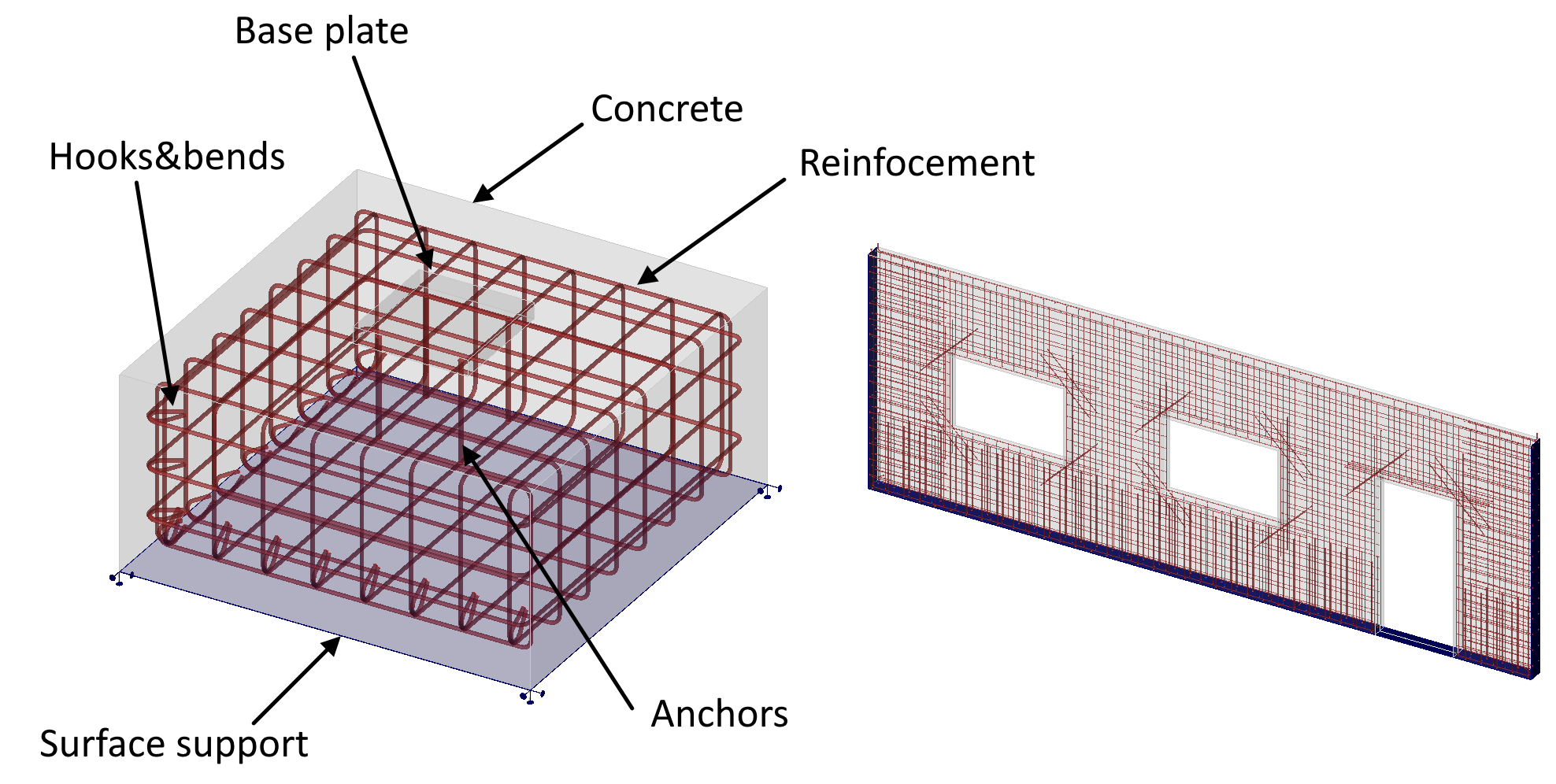
3D CSFM beschouwt continue spanningsvelden in het beton (3D eindige elementen), aangevuld met discrete "staaf" elementen die de wapening voorstellen (1D eindige elementen). Daarom is de wapening niet direct ingebed in de betonnen 3D-eindige elementen, maar expliciet gemodelleerd en ermee verbonden.
\[ \textsf{\textit{\footnotesize{Fig. 9\qquad Rendering of the calculation model for concrete block and out-of-plane wall}}}\]
Typen van Eindige Elementen
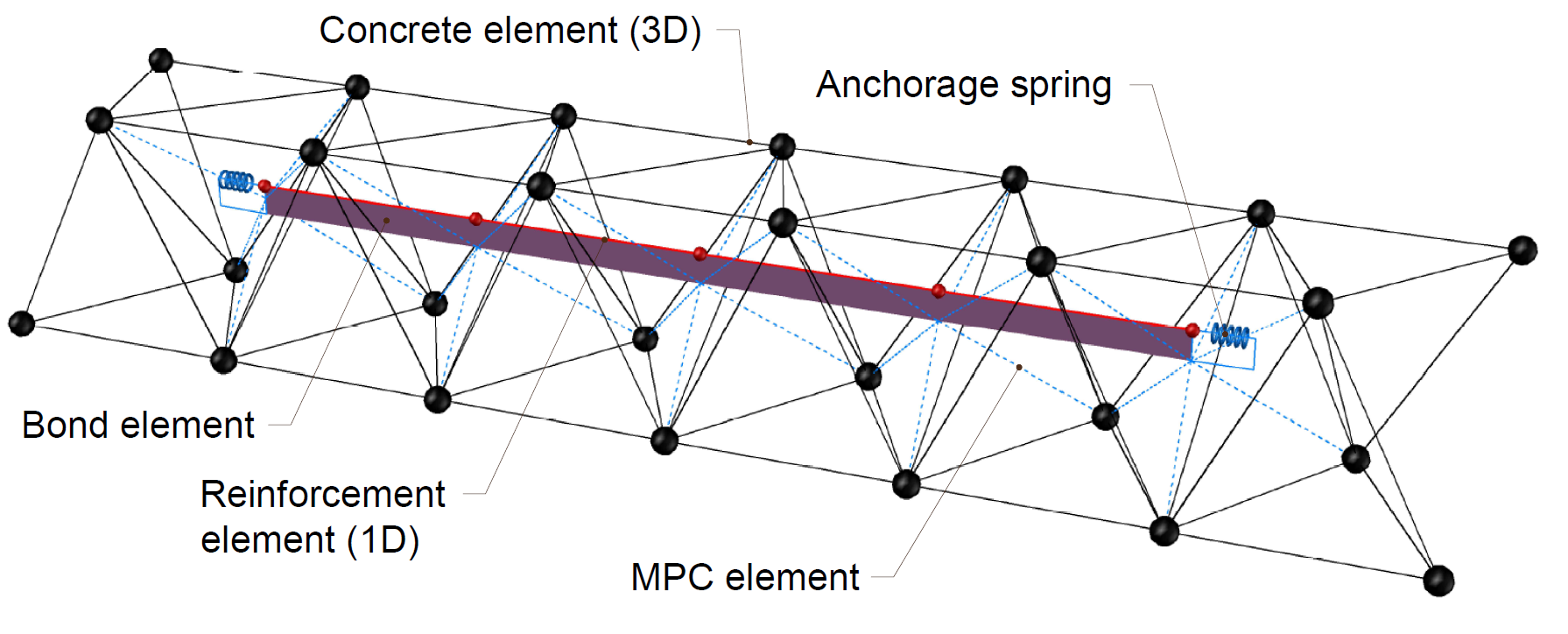
Het niet-lineaire (niet-elastische) eindige elementen berekeningsmodel wordt gecreëerd door verschillende typen eindige elementen die gebruikt worden om beton, wapening en de verbinding daartussen te modelleren. Beton- en wapeningselementen worden eerst onafhankelijk aangemaakt en dan onderling verbonden met behulp van multipoint constraints (MPC-elementen). Hierdoor kan de wapening elke positie innemen die niet beperkt is tot knooppunten van het tetrahedrale net. Om de lengte, aanhechting en verankering te controleren worden veerelementen ingevoegd tussen de wapening en de MPC-elementen.
\[ \textsf{\textit{\footnotesize{Fig. 10\qquad Finite element model: reinforcement elements mapped to concrete mesh using MPC and bond elements}}}\]
Beton
Beton wordt geanalyseerd met gemengde tetraëderelementen met knooppuntrotaties. De tetrahedrale elementen laten ons toe om complexe gebieden te meshen terwijl de geïmplementeerde formulering accurate vervormingsresultaten garandeert (zonder valse schuifspanning gekend als het shear lock effect) zelfs voor de grove mesh die niet geschikt zou zijn voor lineaire tetrahedrale elementen formulering.
Er wordt gebruik gemaakt van volledige integratie. Dit betekent dat elk element vier integratiepunten binnen het volume heeft. Een dergelijke integratie levert een nauwkeurig rek- en spanningsveld op, waardoor de resultaten over het hele volume voldoende geëvalueerd en gepresenteerd kunnen worden. Vervolgens worden de stopcriteria vastgesteld op basis van de waarde in het integratiepunt.
Wapening
Wapeningsstaven worden gemodelleerd door tweeknoops 1D "staaf" elementen (CROD), die alleen axiale stijfheid hebben. Deze elementen zijn verbonden met speciale "bond" elementen die ontwikkeld werden om het slipgedrag tussen een wapeningsstaaf en het omringende beton te modelleren. Deze bond-elementen worden vervolgens verbonden door MPC-elementen (multipoint constraint) met de mesh die het beton voorstelt. Deze aanpak maakt het mogelijk om wapening en beton onafhankelijk van elkaar te meshen.
Bond-elementen (aanhechting)
De verankeringslengte wordt geverifieerd door de schuifspanningen tussen betonelementen (3D) en wapeningsstaafelementen (1D) in het eindige elementenmodel te implementeren. Voor dit doel werd het “bond” eindige-elementtype ontwikkeld.
Het bindingselement wordt gedefinieerd als een eindig element van de schaal dat verbonden is met elementen die de wapening voorstellen door de eerste laag en door de tweede laag met betongaas via meerpuntsbeperkingen (MPC-elementen). Opgemerkt moet worden dat het bond-element in dit artikel altijd wordt weergegeven met een niet-nul hoogte, die echter in het model als oneindig klein wordt gedefinieerd.
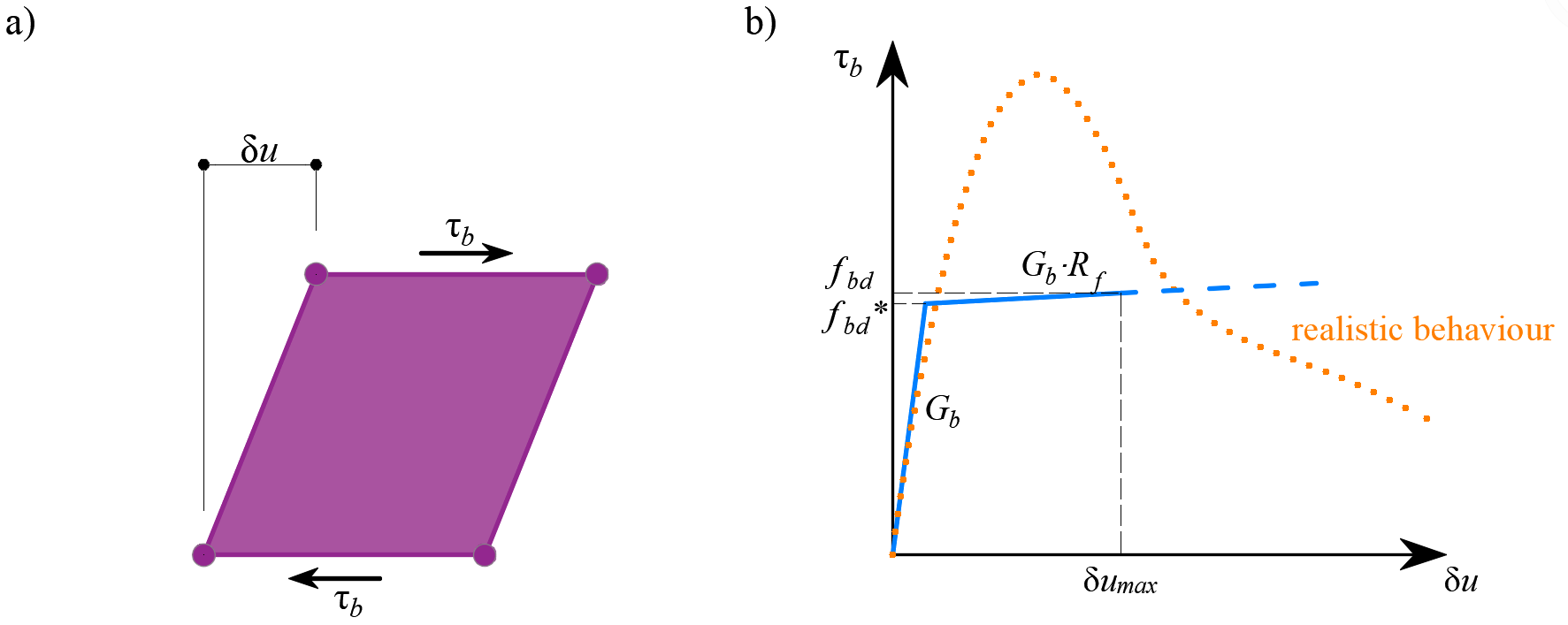
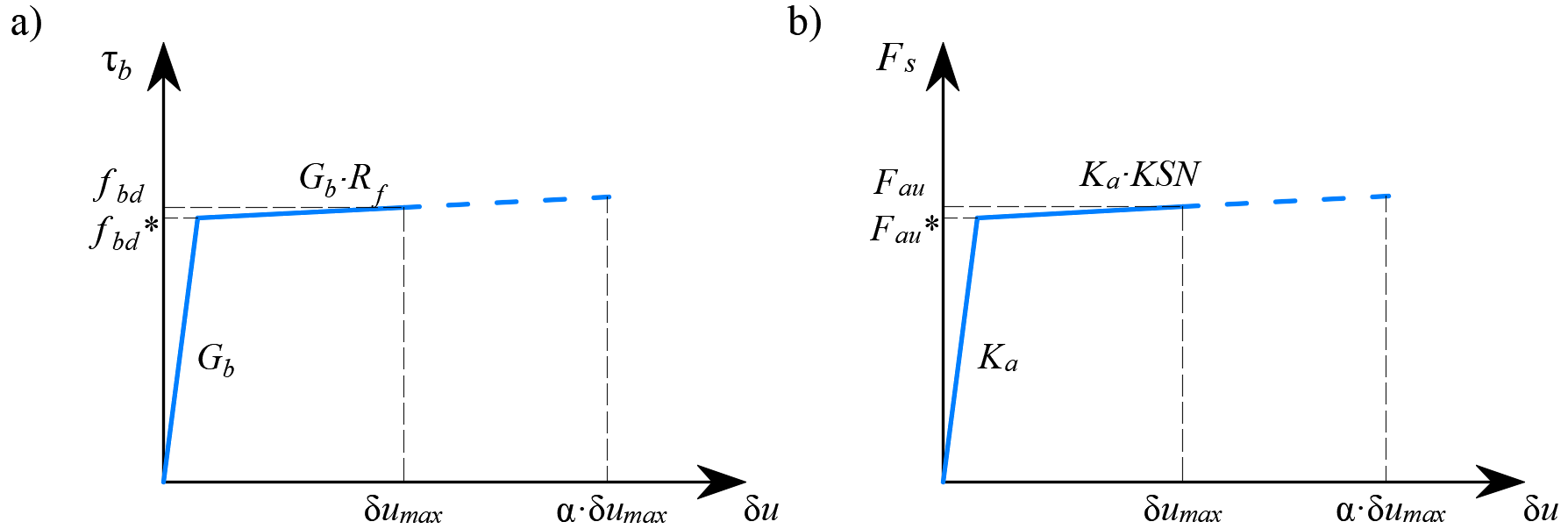
Het gedrag van dit element wordt beschreven door de binding spanning, τb, als een bilineaire functie van de slip tussen de bovenste en onderste knooppunten, δu, zie (Fig. 11).
\[ \textsf{\textit{\footnotesize{Fig. 11\qquad (a) Conceptual illustration of the deformation of a bond element; (b) shear-deformation function}}}\]
De elastische stijfheidsmodulus van de binding-sliprelatie, Gb, wordt als volgt gedefinieerd:
\[G_b = k_g \cdot \frac{E_c}{Ø}\]
kg coëfficiënt afhankelijk van het oppervlak van de wapeningsstaaf (standaard kg = 0,2)
Ec elasticiteitsmodulus van beton (genomen als Ecm in het geval van EN)
Ø de diameter van de betonstaal
De ontwerpwaarden (verdisconteerde waarden) van de uiterste afschuifspanning, fbd, in de respectievelijke geselecteerde ontwerpcodes EN 1992-1-1 of ACI 318-19 worden gebruikt om de verankeringslengte te verifiëren. De verharding van de plastische tak wordt standaard berekend als Gb/105.
Verankeringsveer
Het aanbrengen van verankeringsuiteinden aan de wapeningsstaven (d.w.z. bochten, haken, lussen...), die voldoen aan de voorschriften van de ontwerpcodes, maakt het mogelijk om de basisverankeringslengte van de staven(lb,netto) te verminderen met een bepaalde factor β (hieronder de 'verankeringscoëfficiënt' genoemd). De ontwerpwaarde van de verankeringslengte(lb) wordt dan als volgt berekend:
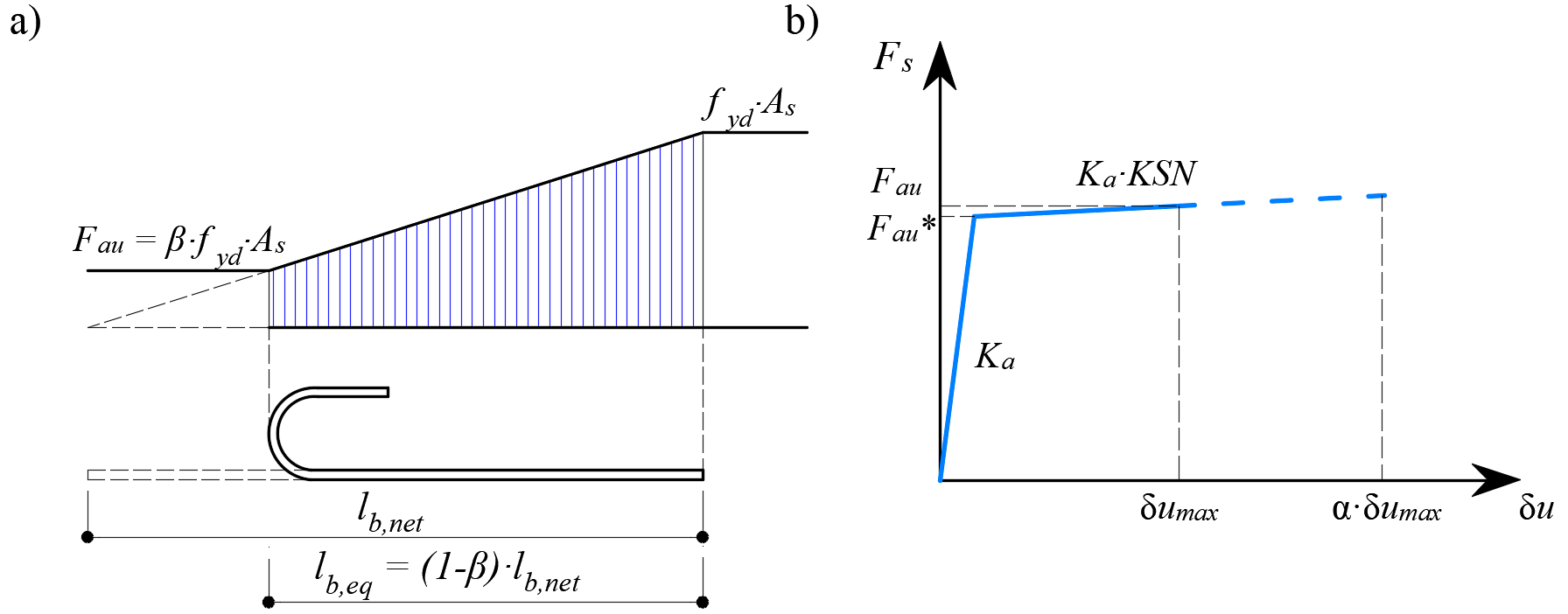
\[ \textsf{\textit{\footnotesize{Fig. 12\qquad Model for the reduction of the anchorage length: a) Anchorage force along the anchorage length of }}}\] \[ \textsf{\textit{\footnotesize{the reinforcement bar, b) slip-anchorage force constitutive law}}}\]
De reductie van de verankeringslengte is opgenomen in het eindige-elementenmodel door middel van een veerelement aan het uiteinde van de staaf (Fig. 12a), die wordt gedefinieerd door het constitutieve model in (Fig. 12b). De maximale kracht die door deze veer wordt overgebracht(Fau) is:
\[F_{au} = \beta \cdot A_s \cdot f_{yd}\]waarbij :
β de verankeringscoëfficiënt gebaseerd op verankeringstype
Als de doorsnede van de wapeningsstaaf
fyd de ontwerpwaarde van de vloeigrens van de wapening
Lastoverdracht componenten
Voetplaat
De voetplaat (staalplaat, oplegplaat, bodemplaat) wordt gemodelleerd als een lineair schaalelement. Het staalmateriaal dat voor platen wordt gebruikt, wordt gedefinieerd in het tabblad Materialen. De enige fysieke eigenschap is de elasticiteitsmodulus E.
\[ \textsf{\textit{\footnotesize{Fig. 13\qquad The base plate material definition}}}\]
De voetplaat kan belast worden door puntlasten (Fx, Fy, Fz, Mx, My, Mz) en krachtgroepen (Fx, Fy, Fz), voornamelijk gebruikt voor het belasten van modellen die geëxporteerd worden uit de IDEA StatiCa Connection. Merk op dat puntbelastingen en puntmomenten direct het corresponderende knooppunt van de staalplaat belasten. Dit betekent dat er geen herverdeling is, alleen door de stijfheid van de staalplaat.
Deze implementatie maakt het mogelijk om belastingseffecten uit de IDEA StatiCa Connection te importeren die worden toegepast op de oplegplaat op de locatie van de individuele eindige laselementen met de waarde en richting bepaald uit de algemene spanning van dat eindige laselement.
Er is alleen wrijvingsdrukcontact gedefinieerd tussen de staalplaat en het beton. Voor de afschuiving kan de gebruiker kiezen uit drie opties:
- Door ankers
- Door wrijving
- Door afschuif kluft
De software staat de combinatie van deze overdrachtsmechanismen niet toe.
De wrijvingscoëfficiënt moet worden ingevoerd als een ontwerp waarde. Als de resulterende dwarskracht Fxy groter is dan de drukkracht Fz maal de wrijvingscoëfficiënt μ stopt de berekening en zijn niet alle belastingen van toepassing op het model. De voorwaarde wordt als volgt geschreven:
\[\frac {F_{xy}}{ \mu \cdot F_{z}}\le 1\]
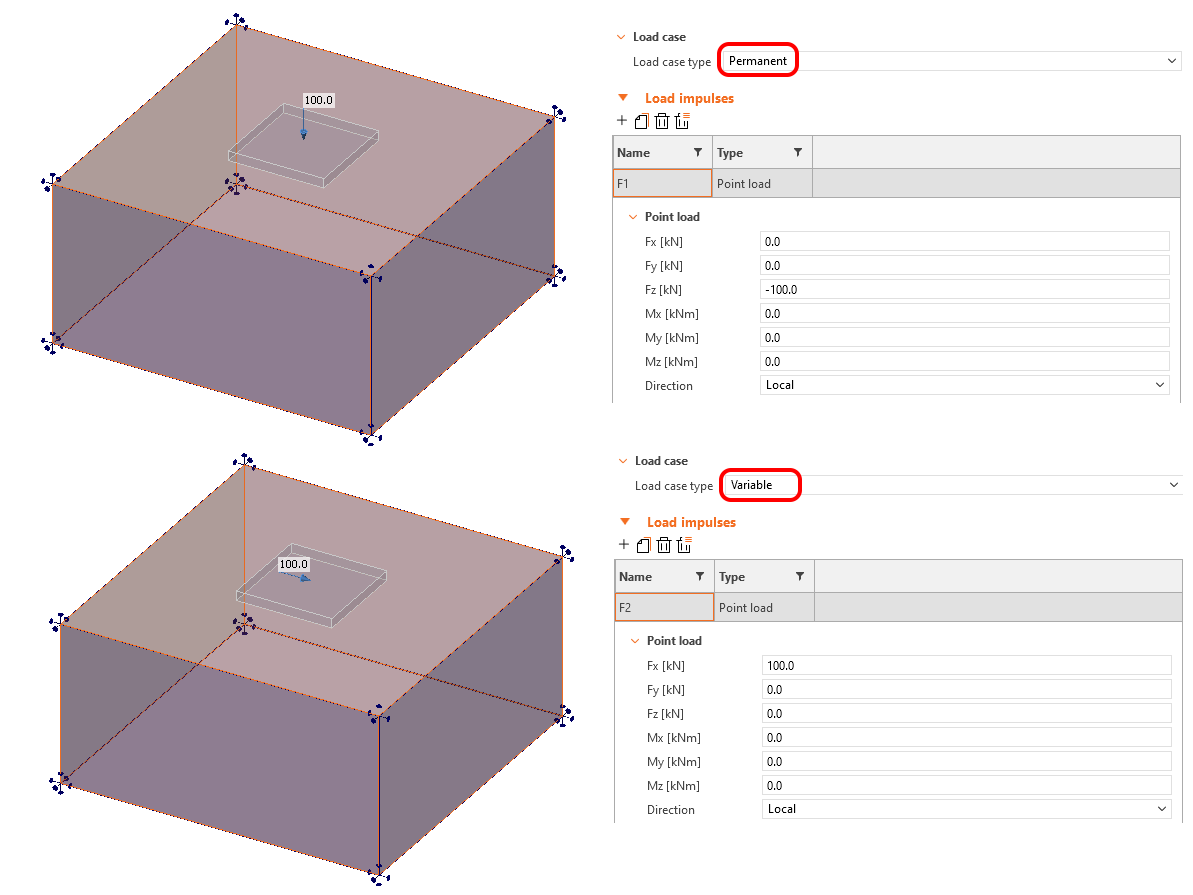
Dit is te zien in het volgende voorbeeld waarbij twee belastingsgevallen worden beschouwd.
- LC1 - Permanent type - Fz = 100 kN
- LC2 - Variabel type - Fx = 100 kN
\[ \textsf{\textit{\footnotesize{Fig. 14\qquad Load input for example explaining shear transfer by friction}}}\]
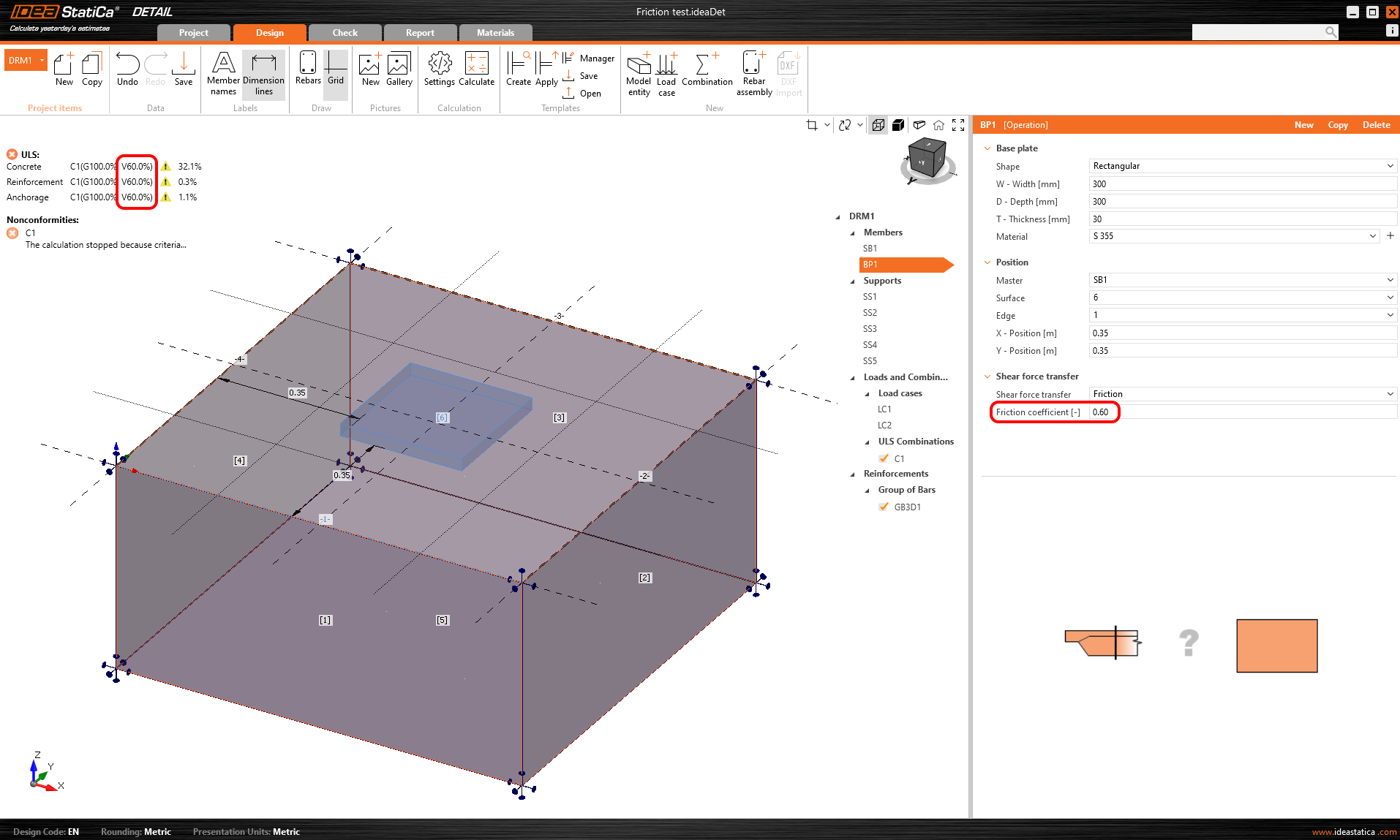
In de eerste berekeningsstap wordt alle permanente belasting aangebracht. Dan wordt de variabele belasting geleidelijk toegepast totdat deze de waarde van de drukbelasting maal wrijvingscoëfficiënt bereikt.
\[ \textsf{\textit{\footnotesize{Fig. 15\qquad Results from example explaining shear transfer by friction}}}\]
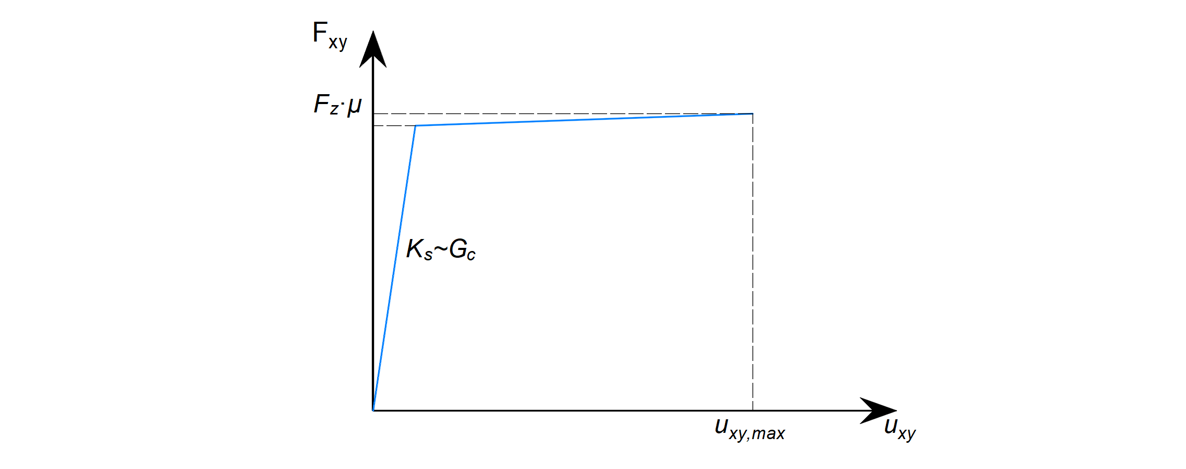
De grafiek in afbeelding 16 definieert het gedrag van het wrijvingscontact tussen de oplegplaat en het beton.
\[ \textsf{\textit{\footnotesize{Fig. 16\qquad Force-displacement graph describing the behavior of frictional contact}}}\]
De waarde van Fzμ verschilt voor elke stap van de berekening, terwijl de waarde van de maximale schuifvervorming uxy constant is.
Als de druknormale kracht Fz en de dwarskracht Fxy worden ingevoerd in één belastingsgevaltype (bijv. alleen permanent) en de voorwaarde Fxy / (Fzμ) ≤ 1 is niet vervuld, dan wordt er geen belasting op het model toegepast omdat de voorwaarde in geen enkele stap van de berekening is vervuld.
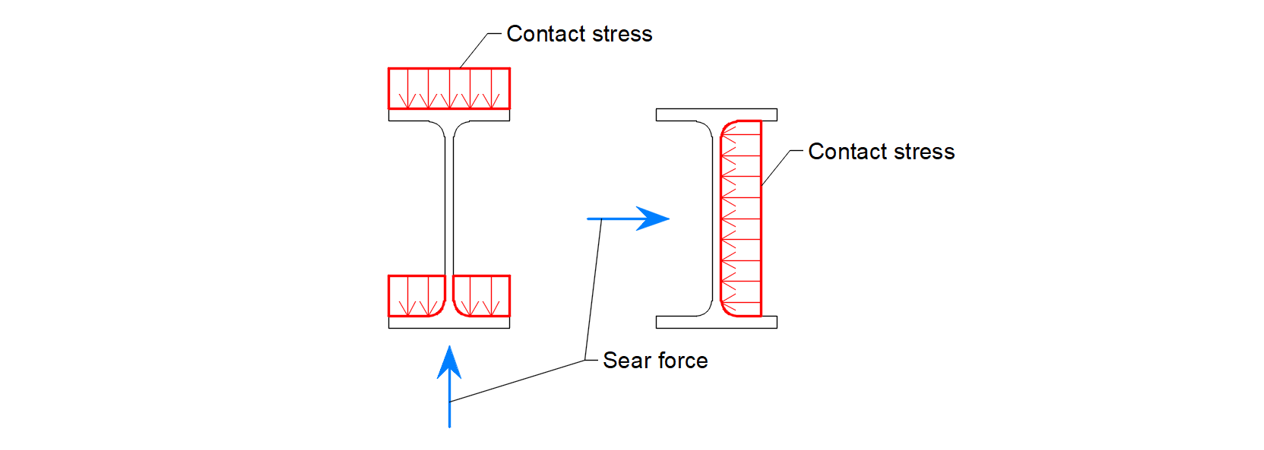
De afschuif kluft is verbonden met het beton door middel van beperkingen die alleen de overdracht van druk en normaal spanning toestaan.
\[ \textsf{\textit{\footnotesize{Fig. 17\qquad Shear lug transfer of shear mechanism}}}\]
De afschuiving wordt gemodelleerd met lineaire schaalelementen, waarbij de elasticiteitsmodulus E het materiaal bepaalt.
De resultaten worden niet geëvalueerd en weergegeven voor zowel de plaat als voor de afschuining.
Ankers
De eindige elementen die ankers voorstellen worden gemodelleerd om normaalkrachten en dwarskrachten te kunnen overbrengen naar het beton, waarbij ook rekening wordt gehouden met de buigstijfheid van de ankers. Om de slip tussen het anker en het omringende beton te modelleren, worden dezelfde hecht- en MPC-elementen gebruikt als voor de wapening. Met dit verschil dat het voor lijmankers mogelijk is om de ontwerp aanhechtsterkte te specificeren.
Ankers kunnen worden verbonden met voetplaten. Voor deze onderlinge verbinding wordt een volledig niet-lineaire constraint gebruikt om het uiteinde van het anker en een knooppunt van de voetplaat te verbinden. Met dit element kunnen we alle vrijheidsgraden controleren om er bijvoorbeeld voor te zorgen dat er geen druk wordt overgebracht door de ankers voor de voetplaat zonder stand-off, of dat er geen afschuiving wordt overgebracht door het anker bij het modelleren van een shear lug, enz.
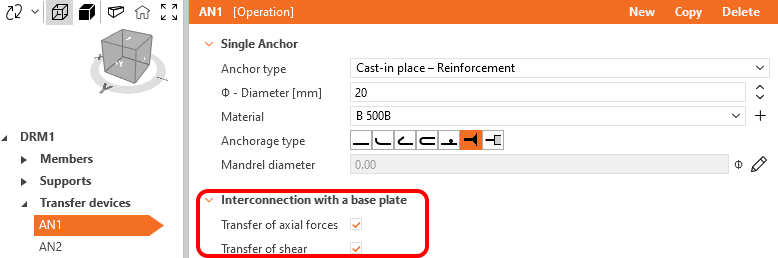
Interconnectie met oplegplaat voor ankers stelt de gebruiker in staat om te bepalen of het anker wordt verbonden met de plaat door de eerder genoemde beperking en hoe.
In de huidige versie wordt alleen het directe contact tussen de plaat en beton ondersteund.
De drukkracht wordt niet overgebracht van de plaat naar het anker in het geval van direct contact. De druk wordt alleen overgebracht door het contact tussen de plaat en het beton.
Het selectievakje Overdracht van axiale krachten kan worden gebruikt om te bepalen of het anker en de oplegplaat al dan niet verbonden zijn in termen van spanning. Dit wordt voornamelijk gebruikt voor de export van de functie Connection (zie het bijbehorende hoofdstuk). Voor handmatige modellering is het zinvol om dit selectievakje altijd aan te vinken.
Het selectievakje Transfer of shear (Overdracht van afschuiving) kan worden gebruikt om te bepalen of het anker en de voetplaat al dan niet verbonden zijn op het vlak van afschuiving. Merk op dat het niet wordt ondersteund om mechanismen voor dwarskrachtoverdracht te combineren, dus voor overdracht door wrijving is dit selectievakje niet relevant. Aan de andere kant, voor afschuiving door middel van ankers, geeft dit veld de optie om sommige ankers uit te sluiten van afschuiving.
Eindige elementen Net in 3D CSFM
De eindige elementen worden intern geïmplementeerd en het berekeningsmodel wordt automatisch gegenereerd zonder dat er gebruikersinteractie nodig is. Een belangrijk onderdeel van dit proces is meshing.
Beton
Alle betonnen elementen worden samengevoegd. De applicatie berekent automatisch een aanbevolen elementgrootte op basis van de grootte en vorm van de constructie en rekening houdend met de diameter van de grootste wapeningsstaaf. Bovendien garandeert de aanbevolen elementgrootte dat er minimaal vier elementen worden gegenereerd in dunne delen van de constructie, zoals slanke kolommen of dunne wanden, om betrouwbare resultaten in deze gebieden te garanderen. Ontwerpers kunnen altijd een door de gebruiker gedefinieerde betonnen elementgrootte kiezen door de vermenigvuldigingsfactor van de standaard meshgrootte aan te passen.
Wapening
De wapening wordt verdeeld in elementen met ongeveer dezelfde lengte als de betonnen elementgrootte. Eens de wapenings- en betonnetten gegenereerd zijn, worden ze onderling verbonden met verbindingselementen, zoals getoond in Fig. 9.
Mesh verfijning
De mesh wordt automatisch verfijnd onder de oplegplaat en rond ankers. De grootte van de verfijnde mesh is standaard twee keer kleiner dan de betonnen basis mesh. De straal van het verfijnde gebied is gedefinieerd als de elementgrootte vermenigvuldigd met twee.
De berekenmethode voor 3D CSFM
Een standaard volledig Newton-Raphson (NR) algoritme wordt gebruikt om de oplossing te vinden voor een niet-lineair FEM probleem.
Over het algemeen convergeert het NR-algoritme niet wanneer de volledige belasting in één stap wordt toegepast. Een gebruikelijke aanpak, die hier ook wordt gebruikt, is om de belasting opeenvolgend toe te passen in meerdere stappen en het resultaat van de vorige stap te gebruiken om de Newton-oplossing van de volgende stap te starten. Hiervoor is een belastingscontrolealgoritme (Load-control Algorithm) geïmplementeerd bovenop de Newton-Raphson. In het geval dat de NR iteraties niet convergeren, wordt de huidige belastingsstap teruggebracht tot de helft van zijn waarde en worden de NR iteraties opnieuw geprobeerd.
Een tweede doel van het Load-control Algorithm is het vinden van de kritische belasting, die overeenkomt met bepaalde "stopcriteria" - specifiek de maximale spanning in beton, de maximale slip in verbindingselementen, de maximale verplaatsing in verankeringselementen en de maximale spanning in wapeningsstaven. De kritische belasting wordt gevonden met de bisectiemethode. Als het stopcriterium ergens in het model wordt overschreden, worden de resultaten van de laatste belastingsstap genegeerd en wordt een nieuwe stap berekend die half zo groot is als de vorige. Dit proces wordt herhaald totdat de kritische belasting is gevonden met een bepaalde fouttolerantie.
Voor beton werd het stopcriterium ingesteld op een spanning van 5% in samendrukking (d.w.z. ongeveer een orde van grootte groter dan de werkelijke bezwijkspanning van beton) en 7% in trek op de integratiepunten van schaalelementen. In trek werd de waarde zo ingesteld dat de grensrek in wapening, die gewoonlijk rond de 5% ligt zonder rekening te houden met trekverstijving, het eerst werd bereikt. In druk werd uit verschillende alternatieven een waarde gekozen die groot genoeg is om de effecten van verbrijzeling (crushing) zichtbaar te maken in de resultaten, maar klein genoeg om niet te veel problemen met de numerieke stabiliteit te veroorzaken.
\[ \textsf{\textit{\footnotesize{Fig 13\qquad Constitutive law of bond and anchorage elements used for anchorage length verification: a) Bond shear stress}}}\] \[ \textsf{\textit{\footnotesize{slip response of bond element, b) force-displacement response of an anchorage element}}}\]
Voor wapening wordt het stopcriterium gedefinieerd in termen van spanningen. Aangezien spanningen bij de scheur worden gemodelleerd, komt het spanningscriterium overeen met de treksterkte van de wapening, rekening houdend met de veiligheidscoëfficiënt. Dezelfde waarde wordt gebruikt voor het criterium in druk.
Het stopcriterium in verbindingselementen en verankeringsveren is α-δumax, waarbij δumax de maximale slip is die gebruikt wordt in de normcontroles en α = 10.
Presentatie van 3D resultaten
De resultaten worden onafhankelijk gepresenteerd voor beton en voor wapeningselementen. De spannings- en rekwaarden in beton worden berekend op de integratiepunten van volume-elementen. Omdat het echter niet praktisch is om de gegevens op een dergelijke manier te presenteren, worden de resultaten standaard gepresenteerd in knooppunten, zoals de maximale waarde van de drukspanning van aangrenzende Gauss-integratiepunten in verbonden elementen. Opgemerkt moet worden dat deze weergave plaatselijk de resultaten aan samengedrukte randen van staven kan onderschatten in een geval waar de eindige-elementgrootte gelijk is aan de diepte van de drukzone.
De resultaten voor de eindige elementen voor wapening zijn ofwel constant voor elk element (één waarde - bijv. voor staalspanningen) of lineair (twee waarden - voor verbindingsresultaten). Voor hulpelementen, zoals elementen van oplegplaten, worden alleen vervormingen weergegeven.
Model geïmporteerd uit IDEA StatiCa Connection
Het IDEA Statica Detail model hoeft niet altijd vanaf nul of een template gemodelleerd te worden. Er is ook een optie om het model inclusief belastingseffecten te importeren uit IDEA StatiCa Connection. De geometrie van het betonblok, ankers, voetplaat, materialen en belastingseffecten worden overgebracht.
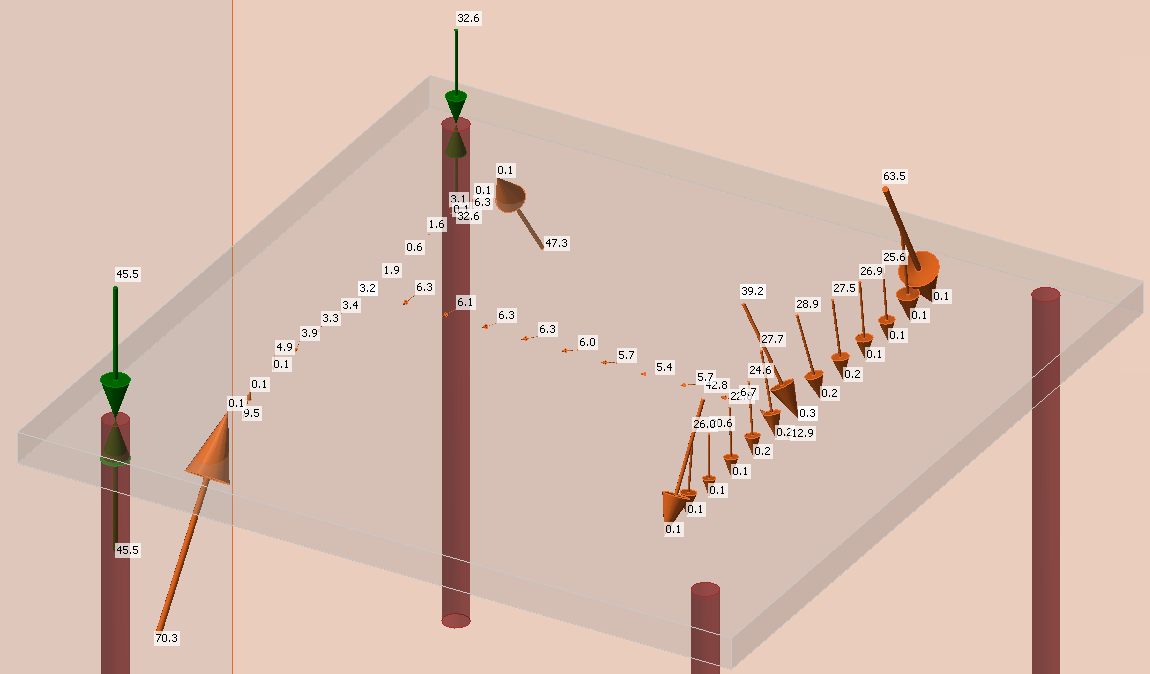
\[ \textsf{\textit{\footnotesize{Fig. 16\qquad Loads imported from IDEA StatiCa Connection}}}\]
De basisplaat wordt belast door een groep krachten die bepaald worden uit de algemene spanning van elk eindig element van de lasnaden die het stalen profiel en de voetplaat verbinden.
Omdat de definitie van de individuele componenten verschillend is in Connection en Detail (de voetplaat wordt bijvoorbeeld gemodelleerd door een lineair materiaal in Detail terwijl het in Connection gemodelleerd wordt door een plastisch materiaal), zou er een verschillende herverdeling van belastingen zijn tussen de voetplaat-beton contact en de ankers, of tussen de ankers zelf. Met andere woorden, er zouden verschillende normaal trekkrachten zijn in de ankers in Connection en Detail. Om deze reden worden de ankers ingevoerd losgekoppeld voor normaalkrachten (in de richting van het anker) van de voetplaat en worden de ankers direct belast met de toegepaste trekkrachten. Ook moeten de tegengestelde krachten die de voetplaat op de ankerlocatie belasten worden toegevoegd om het model in evenwicht te brengen. Deze twee tegengestelde krachten worden getoond in Figuur 16.
De dwarskrachten worden echter overgebracht door de onderlinge verbinding van de voetplaat en het anker (of kluft, of wrijving). Dit gedrag is mogelijk omdat er een beperking is die de voetplaat en het anker verbindt, waardoor we alle vrijheidsgraden van deze verbinding kunnen controleren.
Model verificatie
Grenstoestanden
Uiterste grenstoestand
De verschillende verificaties die vereist zijn door specifieke ontwerpcodes worden beoordeeld op basis van de directe resultaten van het model. UGT-verificaties worden uitgevoerd voor betonsterkte, wapeningssterkte en verankering (afschuifspanningen).
Om er zeker van te zijn dat een constructie-element een efficiënt ontwerp heeft, wordt het sterk aanbevolen om een voorlopige analyse uit te voeren die rekening houdt met de volgende stappen:
- Kies een selectie van de meest kritieke belastingscombinaties.
- Bereken alleen UGT-belastingscombinaties.
- Om de rekentijd te versnellen en eventuele problemen op te lossen, kunt u overwegen een grove mesh te gebruiken door de vermenigvuldigingsfactor van de standaard mesh-grootte in de Setup te verhogen (Fig. 14). Als het model goed presteert, zet de vermenigvuldigingsfactor dan terug op een factor 1.
\[ \textsf{\textit{\footnotesize{Fig 14\qquad Mesh multiplier}}}\]
Een dergelijk model berekent zeer snel, zodat ontwerpers de detaillering van het constructie-element efficiënt kunnen herzien en de berekening opnieuw kunnen uitvoeren totdat aan alle verificatie-eisen is voldaan voor de meest kritische belastingscombinaties. Zodra aan alle verificatievereisten van deze voorlopige analyse is voldaan, wordt voorgesteld om de volledige ultieme belastingscombinaties op te nemen en een fijne mesh te gebruiken (de meshgrootte die door het programma wordt aanbevolen). Gebruikers kunnen de meshgrootte wijzigen met de vermenigvuldigingsfactor, die waarden kan aangepast worden van 0,5 tot 5 (Fig. 14).
De basisresultaten en verificaties (spanning, rek en gebruik (d.w.z. de berekende waarde/limietwaarde van de code)), evenals de richting van de hoofdspanningen in het geval van betonelementen) worden weergegeven door middel van verschillende plots waarbij druk over het algemeen in rood wordt weergegeven en trek in blauw. Globale minimum- en maximumwaarden voor de hele constructie kunnen worden gemarkeerd, evenals minimum- en maximumwaarden voor elk door de gebruiker gedefinieerd onderdeel. In een apart tabblad van het programma kunnen geavanceerde resultaten zoals tensorwaarden, vervormingen van de constructie en wapeningsverhoudingen (effectief en geometrisch) die gebruikt worden voor het berekenen van de Tension Stiffening van wapeningsstaven getoond worden. Verder kunnen belastingen en reacties voor geselecteerde combinaties of belastingsgevallen worden weergegeven.
Constructieve controles volgens Eurocode
Materiaalmodellen in 3D CSFM (Eurocode)
Beton - UGT
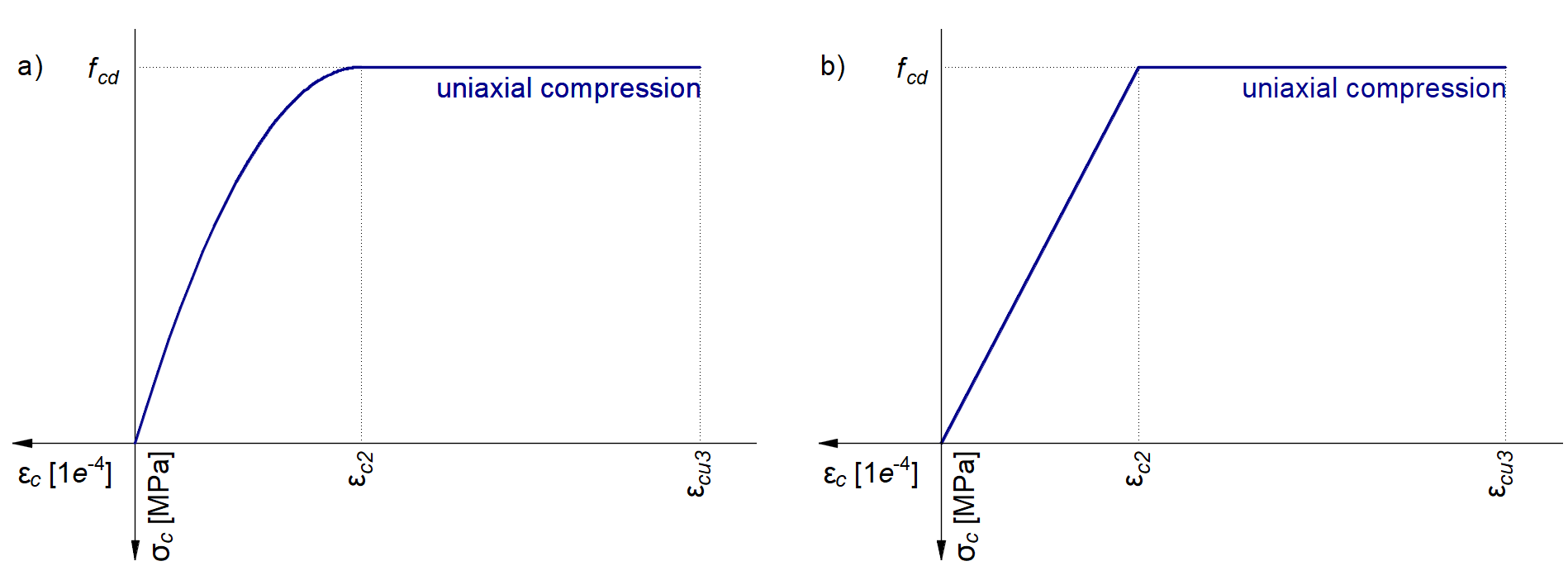
Het betonmodel dat is geïmplementeerd in 3D CSFM is gebaseerd op de constitutieve relaties voor eenassige druk zoals voorgeschreven door EN 1992-1-1 voor het ontwerp van doorsneden, die alleen afhankelijk zijn van de druksterkte. Het parabool-rechthoek diagram zoals gespecificeerd in EN 1992-1-1 Cl. 3.1.7 (1) (Fig. 15a) wordt standaard gebruikt in 3D CSFM, maar ontwerpers kunnen ook kiezen voor een meer vereenvoudigde elastisch-plastische relatie volgens EN 1992-1-1 Cl. 3.1.7 (2) (Fig. 15b). De treksterkte wordt verwaarloosd, zoals in het klassieke ontwerp van gewapend beton.
\[ \textsf{\textit{\footnotesize{Fig 15\qquad The stress-strain diagrams of concrete for ULS: a) parabola-rectangle diagram; b) bilinear diagram}}}\]
De implementatie van 3D CSFM in IDEA StatiCa Detail houdt geen rekening met een expliciet bezwijkcriterium in termen van rek voor beton in druk (d.w.z. na het bereiken van de piekspanning wordt een plastische tak beschouwd met εcu2 (εcu3) in een waarde van 5% terwijl EN 1992-1-1 uitgaat van een uiteindelijke rek van minder dan 0,35%). Met deze vereenvoudiging kan de vervormingscapaciteit van constructies die in druk bezwijken niet worden geverifieerd. Echter, hun uiteindelijke capaciteit fcd volgens EN 1992-1-1 3.1.3 wordt goed voorspeld wanneer de toename in brosheid van beton als de sterkte toeneemt wordt beschouwd door middel van de reductiefactor \(\eta_{fc}\) gedefinieerd in fib Model Code 2010 als volgt:
\[f_{cd}={\alpha_{cc}} \cdot \frac{f_{ck,red}}{γ_c} = {\alpha_{cc}} \cdot \frac{\eta _{fc} \cdot f_{ck}}{γ_c}\]
\[{\eta _{fc}} = {\left( {\frac{{30}}{{{f_{ck}}}}} \right)^{\frac{1}{3}}} \le 1\]
waarbij:
αcc de coëfficiënt is die rekening houdt met langetermijneffecten op de druksterkte en met ongunstige effecten die het gevolg zijn van de manier waarop de belasting wordt uitgeoefend. De coëfficiënt is volgens EN 1992-1-1 Cl. 3.1.6 (1). De standaardwaarde is 1,0.
fck is de cylindrische karakteristieke sterkte van beton (in MPa voor de definitie van \( \eta_{fc} \)).
Wapening
Standaard wordt het bilineaire spanning-rekdiagram voor wapeningsstaven beschouwd zoals gedefinieerd in EN 1992-1-1, paragraaf 3.2.7 (Fig. 16). De definitie van dit diagram vereist alleen dat de basiseigenschappen van de wapening bekend zijn tijdens de ontwerpfase (sterkte en ductiliteitsklasse). Indien bekend, kan de werkelijke spanning-rek relatie van de wapening beschouwd worden. Het spanning-rekdiagram van de wapening kan gedefinieerd worden door de gebruiker, maar in dit geval is het onmogelijk om het Tension Stiffening effect te veronderstellen (het is onmogelijk om de scheurwijdte te berekenen). Het gebruik van het spanning-rekdiagram met een horizontale bovenste tak maakt het niet mogelijk om de constructieve duurzaamheid te verifiëren. Daarom is handmatige verificatie van de standaard vervormbaarheidseisen noodzakelijk.
\[ \textsf{\textit{\footnotesize{Fig. 16 \qquad Stress-strain diagram of reinforcement: a) bilinear diagram with an inclined top branch; b) bilinear diagram}}}\] \[ \textsf{\textit{\footnotesize{with a horizontal top branch.}}}\]
Tension Stiffening (fig. 17) wordt automatisch in rekening gebracht door de spanning-rekrelatie van de wapeningsstaaf te wijzigen om de gemiddelde stijfheid van de staven in het beton (εm) weer te geven.
\[ \textsf{\textit{\footnotesize{Fig. 17 \qquad Scheme of tension stiffening.}}}\]
Partiële veiligheidsfactoren
De Compatible Stress Field Method (CSFM) voldoet aan moderne ontwerpnormen. Omdat de rekenmodellen alleen gebruik maken van standaard materiaaleigenschappen, kan het formaat van de veiligheidsfactoren die in de ontwerpnormen worden voorgeschreven, zonder enige aanpassing worden toegepast. Op deze manier worden de belastingen gefactoriseerd en de karakteristieke materiaaleigenschappen gereduceerd met behulp van de respectieve veiligheidscoëfficiënten die in de ontwerpnormen worden voorgeschreven, precies zoals bij conventionele betonberekeningen. Waarden van materiaalveiligheidsfactoren voorgeschreven in EN 1992-1-1 hfdst. 2.4.2.4 zijn standaard ingesteld, maar de gebruiker kan veiligheidsfactoren wijzigen in de Norm- en berekeningsinstellingen (Afb. 18).
\[ \textsf{\textit{\footnotesize{Fig. 18\qquad De instelling van materiaalveiligheidsfactoren in Idea StatiCa Detail.}}}\]
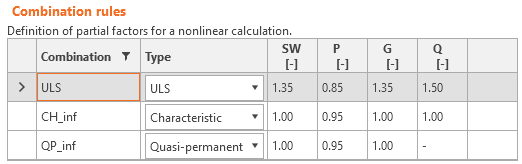
De belastingsveiligheidsfactoren moeten door de gebruiker worden gedefinieerd in Combinatieregels voor elke niet-lineaire combinatie van belastingsgevallen (afb. 19). Voor alle templates die in Idea StatiCa Detail zijn geïmplementeerd, zijn veiligheidsfactoren al voorgedefinieerd.
\[ \textsf{\textit{\footnotesize{Fig. 19\qquad De instelling van partiële belastingsfactoren in Idea StatiCa Detail.}}}\]
Door gebruik te maken van geschikte, door de gebruiker gedefinieerde combinaties van partiële veiligheidsfactoren, kunnen gebruikers met 3D CSFM ook rekenen met de globale weerstandsfactor methode (Navrátil, et al. 2017), maar deze aanpak wordt in de ontwerppraktijk nauwelijks gebruikt. Sommige richtlijnen bevelen het gebruik van de globale weerstandsfactor methode aan voor niet-lineaire analyses. Bij vereenvoudigde niet-lineaire analyses (zoals 3D CSFM), waarbij alleen die materiaaleigenschappen nodig zijn die in conventionele handberekeningen worden gebruikt, is het echter nog steeds wenselijker om het partiële veiligheidsformaat te gebruiken.
Uiterste Grenstoestand (UGT) controles
De verschillende door EN 1992-1-1 vereiste verificaties worden beoordeeld op basis van de directe resultaten van het model. UGT-verificaties worden uitgevoerd voor betonsterkte, wapeningssterkte en verankering (afschuifspanningen).
De betonsterkte in druk wordt geëvalueerd als de verhouding tussen de maximale equivalente hoofdspanning σc,eq verkregen uit de FE-analyse en de grenswaarde σc,lim = fcd.
De equivalente hoofdspanning drukt de equivalente uni-axiale spanning uit voor een algemene tri-axiale spanningstoestand.
\[\sigma_{c,eq} = \sigma_{c3} - \sigma_{c1}\]
De σc,eq waarde kan daarom direct worden vergeleken met de grenswaarden voor deuni-axiale sterkte volgens 1992-1-1 Cl. 3.1.7 (1).
Deze uitdrukking is afgeleid van de toepassing van de Mohr-Coulomb plasticiteitstheorie, waarbij conservatief is aangenomen dat de hoek van inwendige wrijving φ = 0°.
De sterkte van de wapening wordt zowel in trek als in druk geëvalueerd als de verhouding tussen de spanning in de wapening bij de scheuren σsr en de gespecificeerde grenswaarde σs,lim:
\(σ_{s,lim} = \frac{k \cdot f_{yk}}{γ_s}\qquad\qquad\textsf{\small{for bilinear diagram with inclined top branch}}\)
\(σ_{s,lim} = \frac{f_{yk}}{γ_s}\qquad\qquad\,\,\,\,\textsf{\small{for bilinear diagram with horizontal top branch}}\)
waarin:
fyk de vloeigrens van de wapening is volgens EN 1992-1-1 Cl. 3.2.3,
k de verhouding is tussen de treksterkte ftk en de vloeispanning, \(k = \frac{f_{tk}}{f_{yk}}\)
γs is de partiële veiligheidsfactor voor wapening.
De afschuifspanning van de aanhechting wordt onafhankelijk geëvalueerd als de verhouding tussen de bondstress τb berekend door FE-analyse en de uiteindelijke aanhechtsterkte fbd, volgens EN 1992-1-1 hoofdstuk. 8.4.2:
\[\frac{τ_{b}}{f_{bd}}\le 1\]
\[f_{bd} = 2.25 \cdot η_1\cdot η_2\cdot f_{ctd}\]
waarbij:
fctd de ontwerpwaarde is van de betontreksterkte volgens EN 1992-1-1 Cl. 3.1.6 (2). Vanwege de toenemende brosheid van beton met een hogere sterkte is fctk,0.05 beperkt tot de waarde voor C60/75 volgens EN 1992-1-1 Cl. 8.4.2 (2)
η1 is een coëfficiënt die verband houdt met de kwaliteit van de aanhechting en de positie van de staaf tijdens het betonstorten (Fig. 31).
η1 = 1,0 wanneer 'goede' omstandigheden worden verkregen en
η1 = 0,7 voor alle andere gevallen, tenzij kan worden aangetoond dat er 'goede' omstandigheden zijn.
η2 is gerelateerd aan de staafdiameter:
η2 = 1,0 voor Ø ≤ 32 mm
η2 = (132 - Ø)/100 voor Ø > 32 mm
\[ \textsf{\textit{\footnotesize{Fig. 20\qquad EN 1992-1-1 Figure 8.2 - Beschrijving van aanhechtingscondities.}}}\]
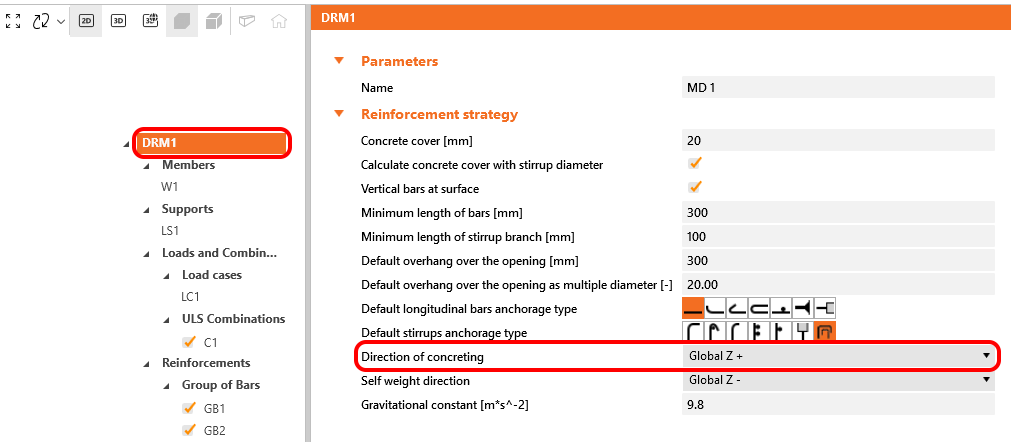
In IDEA StatiCa Detail wordt rekening gehouden met de omstandigheden volgens Fig. 20 c) en d). De betonstortrichting kan in de toepassing voor elk projectonderdeel als volgt worden ingesteld:
\[ \textsf{\textit{\footnotesize{Fig. 21\qquad Richting van betonstorten}}}\]
Deze controles worden uitgevoerd met betrekking tot de juiste grenswaarden voor de respectieve delen van de constructie (d.w.z. ondanks het feit dat er één klasse is voor zowel beton als wapeningsmateriaal, zullen de uiteindelijke spanning-rekdiagrammen verschillen in elk deel van de constructie vanwege verstijvings- en samendrukkingseffecten).
Totale kracht Ftot en limiet kracht Flim
De totale kracht Ftot is een resultaat van de eindige-elementenanalyse en kan op twee manieren worden gedefinieerd.
\[F_{tot}=A_{s}\cdot \sigma_{s}\]
waarbijAs de oppervlakte van de wapeningsstaaf is en σs de spanning in de staaf.
Of als een som van de verankeringskrachtFa en de aanhechtingskracht Fbond.
\[F_{tot}=F_{a}+F_{bond}\]
waarbijFa de werkelijke kracht in de verankeringsveer is en Fbond de aanhechtingskracht die kan worden verkregen door de aanhechtspanning τb te integreren langs de lengte van wapeningsstaaf l.
\[F_{bond}=C_{s} \cdot \int_{0}^{l}\tau_{b}\left( x \right)dx\]
Cs is de omtrek van de wapeningsstaaf.
De limiet kracht Flim is de maximale kracht in het element van de wapening, rekening houdend met de uiterste sterkte van de wapening en ook met de verankeringsomstandigheden (verbinding tussen beton en wapening en verankeringshaken, lussen, enz.)
\[F_{lim}=min\left( F_{lim,bond}+F_{au},F_{u} \right)\]
\[F_{u}=k\cdot f_{yd}\cdot A_{s}\]
\[F_{au}=\beta\cdot k\cdot f_{yd}\cdot A_{s}\]
\[F_{lim,bond}=C_{s}\cdot l \cdot f_{bd}\]
waarbij Cs de omtrek van de wapeningsstaaf is en l de lengte vanaf het begin van de wapening tot aan het punt dat van belang is.
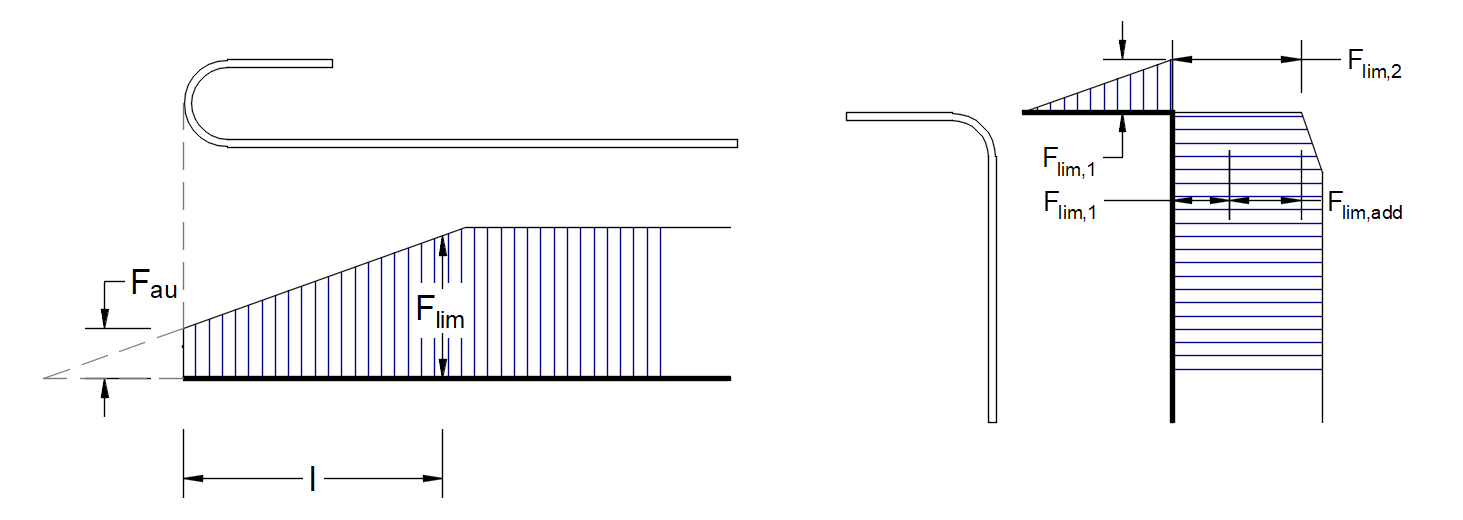
\[ \textsf{\textit{\footnotesize{Fig. 22\qquad Definitie van limiet kracht Flim}}}\]
\[F_{lim,2}=F_{lim,1}+F_{lim,add}\]
waarbijFlim,add de extra kracht is die berekend wordt uit de grootte van de hoek tussen naburige elementen.Flim,2 moet altijd lager zijn danFu.
De beschikbare verankeringstypes in 3D CSFM omvatten een rechte staaf (d.w.z. zonder reductie van het ankereinde), bocht, haak, lus, gelaste dwarsstaaf, perfecte verbinding en doorlopende staaf. Al deze types, samen met de respectievelijke verankeringscoëfficiënten β, worden getoond in Fig. 23 voor langswapening en in Fig. 24 voor beugels. De waarden van de aangenomen verankeringscoëfficiënten zijn in overeenstemming met EN 1992-1-1 paragraaf 8.4.4 Tab. 8.2. Er dient opgemerkt te worden dat ondanks de verschillende beschikbare opties, 3D CSFM drie types verankeringseinden onderscheidt: (i) geen reductie van de verankeringslengte, (ii) een reductie van 30% van de verankeringslengte in het geval van een genormaliseerde verankering en (iii) perfecte aanhechting.
\[ \textsf{\textit{\footnotesize{Fig. 23\qquad Beschikbare verankeringstypes in 3D CSFM:}}}\]
\[ \textsf{\textit{\footnotesize{(a) recht; (b) bocht; (c) haak; (d) lus; (e) gelast; (f) perfecte aanhechting; (g) doorgaande staaf.}}}\]
\[ \textsf{\textit{\footnotesize{Fig. 24\qquad Beschikbare verankeringstypes en respectievelijke verankeringscoëfficiënten voor beugels.}}}\]
\[ \textsf{\textit{\footnotesize{Gesloten beugels: (a) haak; (b) bocht; (c) overlap. Open beugels: (d) haak; (e) doorgaande staaf.}}}\]
Om te voldoen aan EN 1992-1-1, moet wapening altijd gemodelleerd worden met rechte uiteinden en moet de verankeringseigenschap gebruikt worden (een verankeringsveer moet toegepast worden). Het modelleren van de verankeringshaak door het direct wijzigen van de wapeningsgeometrie is niet in overeenstemming met EN 1992-1-1.
Maak vandaag nog een proefrit met de nieuwste IDEA StatiCa
Verificaties en validaties
Eenheidstest: Eenvoudige buigproef op trilbalken
Eenheidstest: Afschuifproeven in liggers met weinig beugels
Tri-axiale spanning - het actieve opsluitingseffect
Kolommen onderworpen aan hoge drukbelasting - Passief opsluitingseffect
Uittrekgedrag van gegoten ankers met verschillende inbeddiepten
Referenties
- Wu, D.; Wang, Y.; Qiu, Y.; Zhang, J.; Wan, Y.-K. Determination of Mohr-Coulomb Parameters from Nonlinear Strength Criteria for 3D Slopes. Math. Probl. Eng. 2019, 6927654.
- Lelovic, S.; Vasovic, D.; Stojic, D. Determination of the Mohr-Coulomb Material Parameters for Concrete under Indirect Tensile Test. Tech. Gaz. 2019, 26, 412-419.
- Galic, M.; Marovic, P.; Nikolic, Ž. Modified Mohr-Coulomb-Rankine material model for concrete. Eng. Comput. 2011, 28, 853-887.
- Fan, Q.; Gu, S.C.; Wang, B.N.; Huang, R.B. Two Parameter Parabolic Mohr Strength Criterion Applied to Analyze The Results of the Brazilian Test. Appl. Mech. Mater. 2014, 624, 630-634.