Vermoeiings analyse – Stompe las van gewalste doorsnede
Omschrijving
Two beams of section IPE 200 from steel grade S355 are welded together by transverse full penetration butt welds. The beams at the position of the investigated detail are loaded by bending moment and normal stress:
Twee liggers van doorsnede IPE 200; staalkwaliteit S355 zijn aan elkaar gelast door middel van stuiklassen met volledige doorlassing. De liggers ter plaatse van het onderzochte detail worden belast door buigmoment en normaalkracht:
| Normaalkracht N [kN] | Buig moment My [kNm] | |
| Minimum | 100 | 10 |
| Maximum | 300 | 30 |
Bepaling van nominale spanning
Veiligheids factor \(\gamma_{Mf}\) wordt geselecteerd uit table 3.1 (EN 1993-1-9). Voor dit voorbeeld, wordt aangemeomen \(\gamma_{Mf} = 1.15\).
| Beoordelingsmethode | Gevolg van falen | |
| Lage gevolgen | hoge gevolgen | |
| Schade tolerant | 1 | 1.15 |
| Levensreddend | 1.15 | 1.35 |
Analytische methode
De nominale spanning is bepaald door een simpele formule :
\[\sigma = \frac{N}{A} + \frac{M_y}{W_y} \]
Voor minimale normaal spanning :
\[\sigma_{min} = \frac{100 \cdot 10^3}{2850} + \frac{10 \cdot 10^6}{194000} = 86.6 \, \textrm{MPa}\]
Voor maximale normaal spanning :
\[\sigma_{max} = \frac{300 \cdot 10^3}{2850} + \frac{30 \cdot 10^6}{194000} = 259.9 \, \textrm{MPa}\]
Het spannings bereik is:
\[\sigma_{max} - \sigma_{min} = 259.9 - 86.6 = 173.3 \, \textrm{MPa} \]
Er is geen schuifspanning. De spanningsconcentratiefactor kf wordt geselecteerd voor het juiste detail. Voor stompe lassen met volledige doorlassing over de hele doorsnede belast door normaalkracht, is de spanningsconcentratiefactor kf = 1.0.
\[\Delta \sigma_R = \gamma_{Mf} \cdot k_f \cdot (\sigma_{max} - \sigma_{min}) = 1.15 \cdot 1.0 \cdot 173.3 = 199.3\,\textrm{MPa} \]
CBFEM berekening
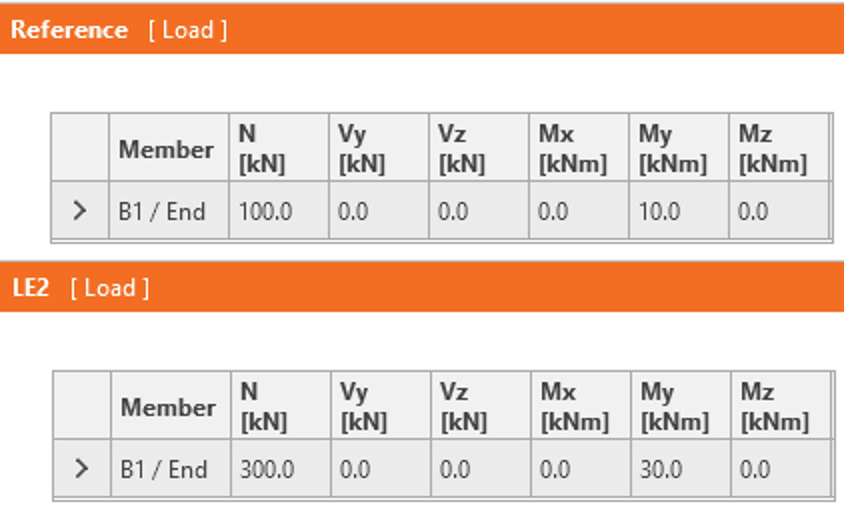
De lasteffecten zijn als volgt ingesteld:
Referentie lasteffect is de minimale last en LE2 is de maximale last.
De von Mises spanning op maximale last (LE2) laat geen component vloeit.
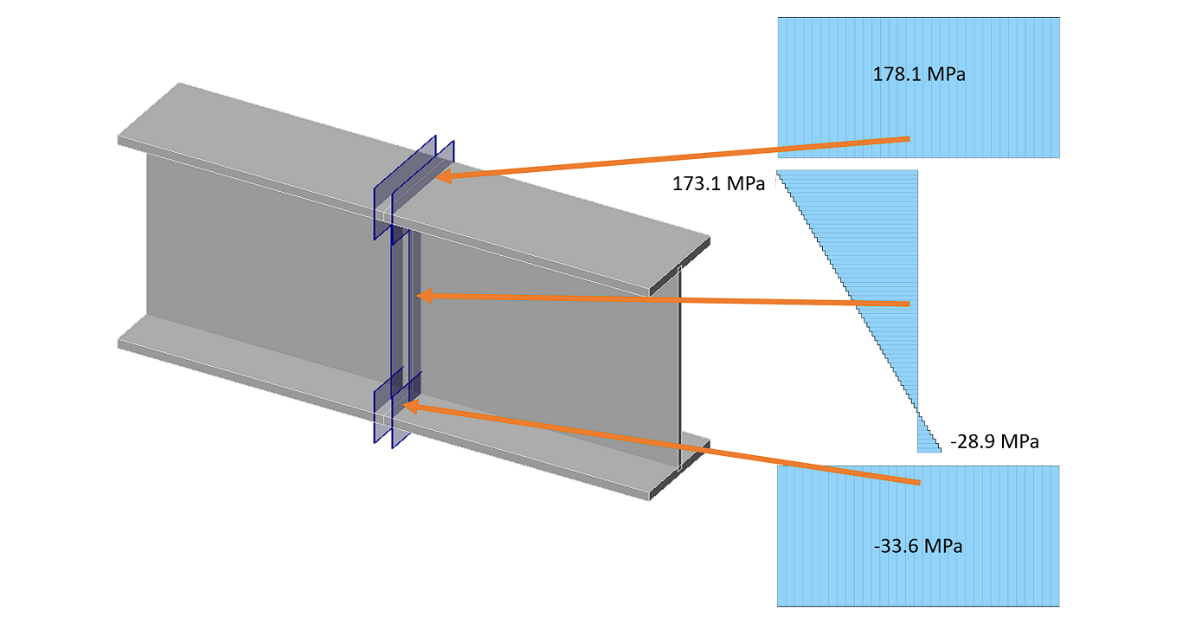
Vlakbij de stompe lasnaden worden automatisch vlakken gegenereerd en de spanningen worden weergegeven in de controletabel:
De spanningsconcentratiefactor kf is afkomstig van de eindige elementenmethode en hoeft niet opnieuw te worden toegepast. De veiligheidsfactor moet worden gebruikt.
\[\Delta \sigma_R = \gamma_{Mf} \cdot \sigma_{max} = 1.15 \cdot 178.1 = 204.8\,\textrm{MPa} \]
Vergelijking
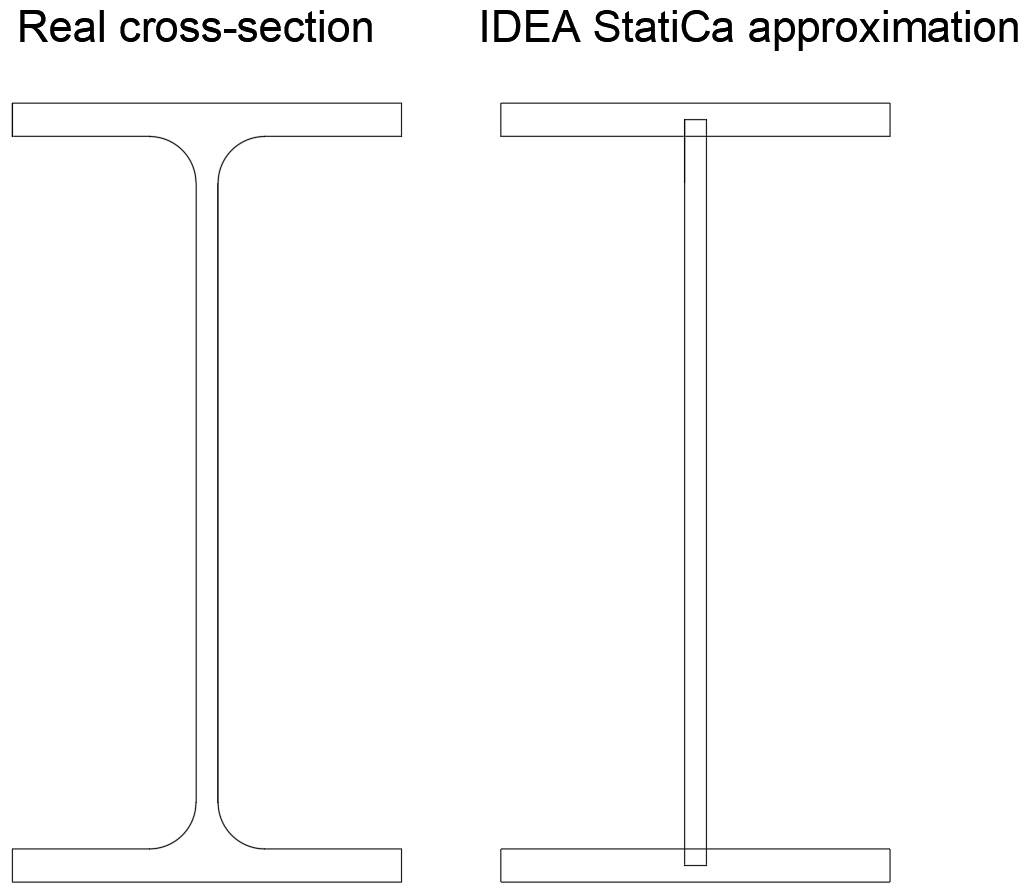
IDEA StatiCa vertoont een iets hogere normaalspanning (178,1 MPa) dan de analytische benadering (173,3 MPa). Het enige verschil wordt veroorzaakt door de veronderstelde doorsnede in IDEA StatiCa met iets andere doorsnedeparameters:
| Werkelijke doorsnede | Aangenomen doorsnede IDEA StatiCa | |
| A | 2850 mm2 | 2772 mm2 |
| Wy | 194 000 mm3 | 188 732 mm3 |
Met behulp van de dwarsdoorsnede-eigenschappen van een vereenvoudigde dwarsdoorsnede worden dezelfde resultaten als IDEA StatiCa verkregen: \(\sigma_{min} = 89.1\,\textrm{MPa}\), \(\sigma_{max} = 267.2\,\textrm{MPa}\), \(\sigma_{max} - \sigma_{min} = 178.1\,\textrm{MPa}\).
Vermoeiings analyse
Een voorbeeld van vermoeiingsanalyse met nominale spanning wordt getoond voor een ontwerp volgens EN 1993-1-9:2005.
De Detailcategorie 90 is geselecteerd uit Tabel 8.3.
Voor nominale spanningsbereiken met constante amplitude is het aantal cycli voor de vermoeiingslevensduur overgenomen uit hoofdstuk 7.1:
\[N_R = \frac{\Delta \sigma_c^m \cdot 2\cdot 10^6}{\Delta \sigma_R^m}\]
Hand berekening:
\[N_R = \frac{90^3 \cdot 2\cdot 10^6}{199.3^3} = 184\,177\, \textrm{cycles}\]
IDEA Connection:
\[N_R = \frac{90^3 \cdot 2\cdot 10^6}{204.8^3} = 169\,734 \, \textrm{cycles}\]
Het aantal cycli dat de staalverbinding kan weerstaan is iets lager in IDEA Connection door de vereenvoudiging van de doorsnede
Benchmark case
Inputs
Aangesloten staven: B1, B2 - IPE200
Staal kwaliteit : S 355
Last effecten:
- Referentie: N = 100 kN, My = 10 kNm
- LE2: N = 300 kN, My = 30 kNm
Bewerkingen: Snede (verstelsnede), Stompe lassen
Outputs
Maximale normaal spanningsbereik : 178.1 MPa bij bovenflens
Afschuifspanningsbereik : 0 MPa