Vermoeiings berekening volgens EN 1993-1-9
Dit artikel laat zien hoe u de nominale spanningen van IDEA Connection kunt gebruiken om volledige vermoeiingsanalyses uit te voeren volgens EN 1993-1-9.
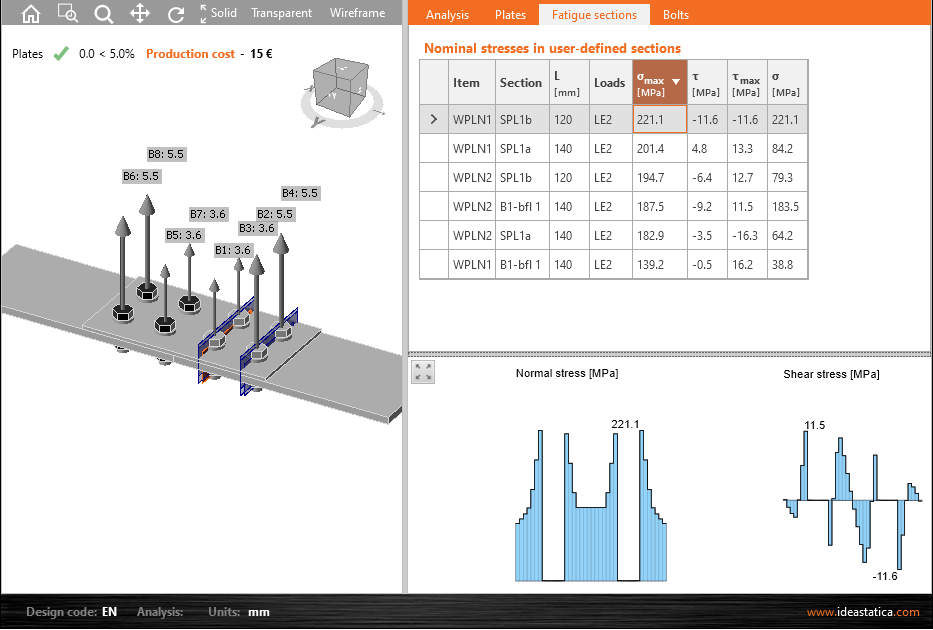
IDEA Connection geeft nominale spanningen in:
- gebruikers-gedefinieerde secties
- secties nabij lassen
- bouten en ankers
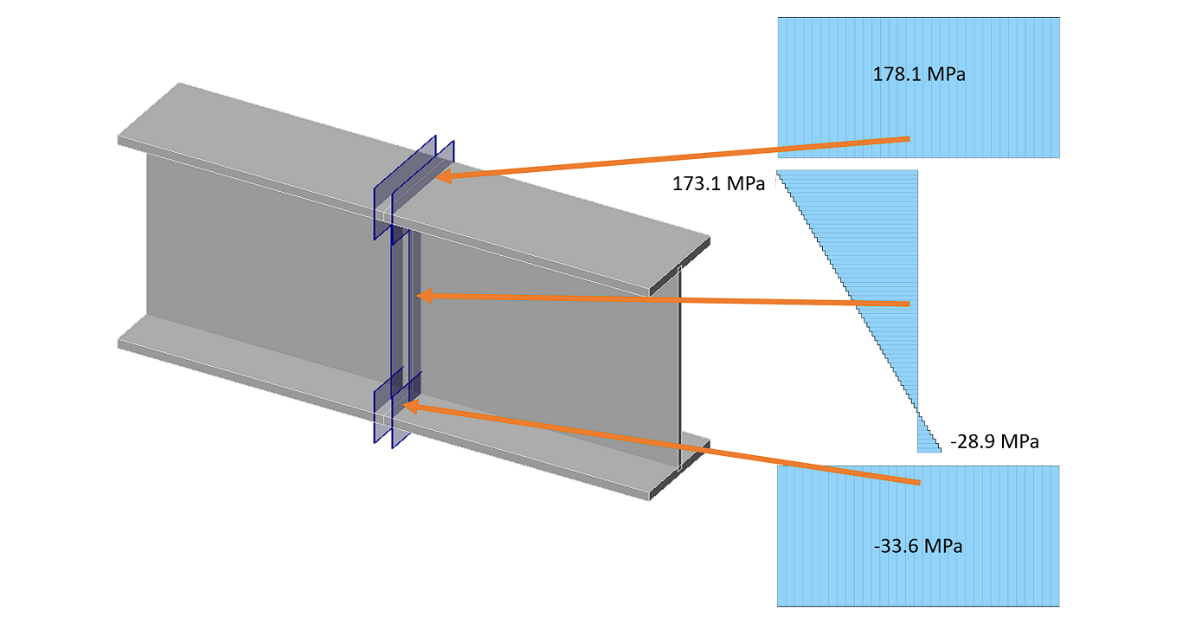
De opgegeven spanningen zijn het spanningsbereik tussen het lasteffect en het referentie-lasteffect. Het spanningsbereik wordt op geen enkele manier gewijzigd, b.v. in termen van de onderstaande afbeelding, die het mogelijk maakt het spanningsbereik te verkleinen als de spanning verandert van trek naar druk.
Deze spanningen omvatten enkele spanningsconcentratiefactoren, b.v. concentratie van spanningen in de buurt van boutgaten.
Andere factoren, b.v. partiële factor voor equivalente spanningsbereiken met constante amplitude \(\gamma_{Ff}\) volgens EN 1991 of k1 factoren voor holle profielverbindingen als gevolg van verwaarloosde buigmomenten in truss-model moeten nog worden opgenomen.
IDEA Connection geeft \(\sigma_{max}\) and \(\tau_{max}\) kan worden gebruikt om te achterhalen \sigma\) en \(\Delta \tau\).
\[ \Delta \sigma = \gamma_{Ff} \cdot k_x \cdot \sigma_{max}\]
\[ \Delta \tau = \gamma_{Ff} \cdot k_x \cdot \sigma_{max}\]
waar:
- \(\gamma_{Ff}\) – partiële factor voor equivalente constante amplitude spanningsbereik
- \(k_x\) – elke factor niet inbegrepen in de analyse, bijv. \(k_1\) from Tabel 4.1 of 4.2
- \(\sigma_{max}\) – IDEA Connection output van normaalspanning
- \(\tau_{max}\) – IDEA Connection output van schuifspanning
Volgens hoofdstuk 8, verg. (8.1), volgend de spannings limieten moet worden voldaan:
\[\Delta \sigma \le 1.5 f_y\]
\[\Delta \tau \le 1.5 f_y / \sqrt{3}\]
where \(f_y\) is staal vloeigrens.
Het detail moet worden gecategoriseerd volgens de tabellen 8.1–8.10 en er moet rekening worden gehouden met alle relevante factoren, b.v. de factor voor grootte-effecten. De detailcategorie (verkleind met bijv. grootte-effectfactor) geeft de vermoeiingssterkte bij 2 miljoen cycli, \(\Delta \sigma_c\) en \(\Delta \tau_c\). De waarden van \(\Delta \sigma_c\) en \(\Delta \tau_c\) moeten worden verminderd met een partiële factor voor vermoeiingssterkte, \(\gamma_{Mf}\).
Tabel 3.1 van EN 1993-1-9 met waardes van \(\gamma_{Mf}\):
| Assessment methode | Gevolg van falen | |
| Lage consequentie | Hoge consequentie | |
| Schade tolerant | 1 | 1.15 |
| Levensreddend | 1.15 | 1.35 |
De limieten van S-N (stress-life) curve worden bepaald volgens hoofdstuk 7.1:
\[\Delta \sigma_D = \left ( \frac{2}{5} \right )^{1/3} \Delta \sigma_c \]
\[\Delta \sigma_L = \left ( \frac{5}{100} \right )^{1/5} \Delta \sigma_D \]
\[\Delta \tau_L = \left ( \frac{2}{100} \right )^{1/5} \Delta \tau_c \]
Volgens hoofdstuk A.5, moeten cycli tot falen moeten worden bepaald. Aantal cycli, \(n_{Ei}\), geassocieerd met spanningsbereik \(\gamma_{Ff} \Delta \sigma_i\), is een invoer van de gebruiker. \(N_{Ri}\) wordt berekend volgens hoofdstuk 7.
Normaalspanningen voor \(\Delta \sigma \ge \Delta \sigma_D\):
\[N_R = \frac{\Delta \sigma_c^m \cdot 2\cdot 10^6}{\Delta \sigma^m}\]
waar:
- m = 3 – helling van de curve van de vermoeiingsssterkte
Normaalspanningen voor \(\Delta \sigma \ge \Delta \sigma_L\):
\[N_R = \frac{\Delta \sigma_D^m \cdot 5\cdot 10^6}{\Delta \sigma^m} \]
waar:
- m = 5 – helling van de curve van de vermoeiingsssterkte
De normaalspanningen onder de grenswaarde \(\Delta \sigma_L\) dragen niet bij aan vermoeiingsschade.
Schuifspanningen voor \(\Delta \tau_E \le \Delta \tau_L\):
\[N_R = \frac{\Delta \tau_c^m \cdot 2\cdot 10^6}{\Delta \tau^m} \]
waar:
- m = 5 – helling van de curve van de vermoeiingsssterkte
De schuifspanningen onder de grenswaarde \(\Delta \tau_L\) nemen niet deel aan vermoeiingsschade.
De schade wordt berekend volgens de Palmgren-Miner-regel (Figuur A.1) in vergelijkingen (A.1) en (A.2) afzonderlijk voor normaal en schuifspanning:.
\[D_d = \Sigma_i^n \frac{n_{Ei}}{N_{Ri}} \le 1.0\]
De normaalspanning en schuifspanning moeten worden gecombineerd door vergelijking (8.3), tenzij anders vermeld in tabellen 8.8 en 8.9.
\[D_{d \sigma}^3 + D_{d \tau}^5 \le 1.0 \]
Voorbeeld
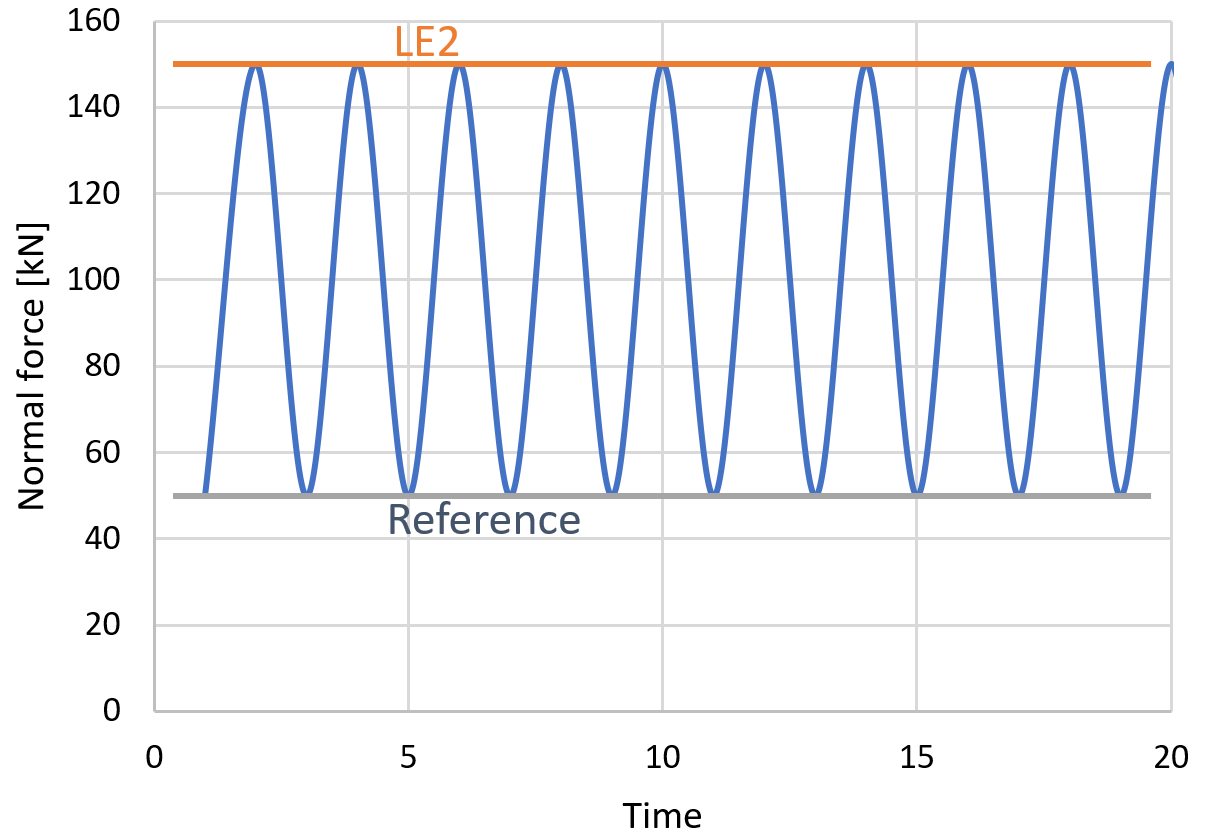
Invoer voor berekening: De gebruiker stelt een referentiebelastingseffect en drie vermoeiingslasteffecten in. De outputs van IDEA Connection zijn de maximale normaalspanning en de bijbehorende schuifspanning. De staalsoort is S355.
| Lasteffect | Aantal cycli | Maximale normaalspanningen | Corresponderende schuifspaninng |
| nE | Δσmax [MPa] | Δτ [MPa] | |
| LE2 | 1 500 000 | 60 | 60 |
| LE3 | 3 000 000 | 50 | 40 |
| LE4 | 10 000 000 | 20 | 10 |
Veiligheidsfactoren zijn bepaald uit EN 1991 en EN 1993-1-9:
\[ \gamma_{Ff} = 1.0 \]
\[ \gamma_{Mf} = 1.15 \]
Spanningbeperkingen worden gecontroleerd:
\[\Delta \sigma \le 1.5 f_y\]
\[ 60 \, \textrm{MPa} \le 1.5 \cdot 355 = 532 \, \textrm{MPa}\]
\[\Delta \tau \le 1.5 f_y / \sqrt{3} \]
\[60 \, \textrm{MPa} \le 1.5 \cdot 355 / \sqrt{3} = 307 \, \textrm{MPa} \]
Uit tabellen 8.1–8.10 worden waarden van \(\Delta \sigma_c = 90\,\textrm{MPa}\) en \(\Delta \tau_c = 70\,\textrm{MPa}\) bepaald. Deze waarden worden verminderd met een partiële factor voor vermoeiingssterkte, \(\gamma_{Mf} = 1.15\) tot \(\Delta \sigma_c = 78.3\,\textrm{MPa}\) en \(\Delta \tau_c = 60.9\,\textrm{MPa}\).
De limieten van de S-N-curve worden bepaald:
\[\Delta \sigma_D = \left ( \frac{2}{5} \right )^{1/3} \Delta \sigma_c = \left ( \frac{2}{5} \right )^{1/3} 78.3 = 57.7\,\textrm{MPa}\]
\[\Delta \sigma_L = \left ( \frac{5}{100} \right )^{1/5} \Delta \sigma_D = \left ( \frac{5}{100} \right )^{1/5} 57.7 = 31.7 \,\textrm{MPa}\]
\[\Delta \tau_L = \left ( \frac{2}{100} \right )^{1/5} \Delta \tau_c = \left ( \frac{2}{100} \right )^{1/5} 60.9 = 27.8\,\textrm{MPa} \]
\(\Delta \sigma\) wordt bepaald door \(\Delta \sigma_{max}\) te vermenigvuldigen met een factor voor equivalente spanningsbereiken met constante amplitude \(\gamma_{Ff} = 1,0\). In dit voorbeeld is geen andere factor kx nodig.
Aantal cycli tot falen, \(N_R\) wordt berekend voor elk belastingsgeval en de normaal- en schuifspanning volgens de bovengenoemde formules, b.v. voor normaalspanning in LE2:
\[N_R = \frac{\Delta \sigma_c^m \cdot 2\cdot 10^6}{\Delta \sigma^m} = \frac{78.3^3 \cdot 2\cdot 10^6}{60^3} = 4 \,438\, 234 \, \textrm{cycles}\]
| Lasteffect | Aantal cycli | Maximale normaal spanning | Corresponderende schuifspanning | Aantal cycli tot falen | Aantal cycli tot falen | ||
| nE | Δσmax [MPa] | Δτ [MPa] | Δσ [MPa] | NR | Δτ [MPa] | NR | |
| LE2 | 1 500 000 | 60 | 60 | 60 | 4 438 235 | 60 | 2 149 190 |
| LE3 | 3 000 000 | 50 | 40 | 50 | 10 200 230 | 40 | 16 320 409 |
| LE4 | 10 000 000 | 20 | 10 | 20 | infinity | 10 | infinity |
Met behulp van de Palmgren-Miner-regel wordt de geaccumuleerde schade berekend voor alle lasteffecten.
Voor normaalspanningen:
\[D_{d \sigma} = \Sigma_i^n \frac{n_{Ei}}{N_{Ri}} = \frac{1\, 500\, 000}{4\, 438\, 235} + \frac{3\,000\,000}{10\,200\,230} = 0.632 \le 1.0\]
Voor schuifspanningen:
\[D_{d \tau} = \Sigma_i^n \frac{n_{Ei}}{N_{Ri}} = \frac{1\, 500\, 000}{2\, 149\, 190} + \frac{3\,000\,000}{16\,320\,409} = 0.882 \le 1.0\]
Ten slotte wordt de interactie tussen normaal- en schuifspanning gecontroleerd:
\[ D_{d \sigma} ^3 + D_{d \tau} ^5 \le 1.0\]
\[ 0.632 ^3 + 0.882 ^5 = 0.786 \le 1.0\]
De weerstand tegen vermoeiing van het onderzochte detail is voldoende.
Verificaties
Voordat het gereedschap voor vermoeiingsanalyse werd vrijgegeven, zijn er verschillende experimentele verificaties uitgevoerd:
Fatigue life by nominal stress method
Vermoeiingsanalyse - Stuiklassen van I-profiel