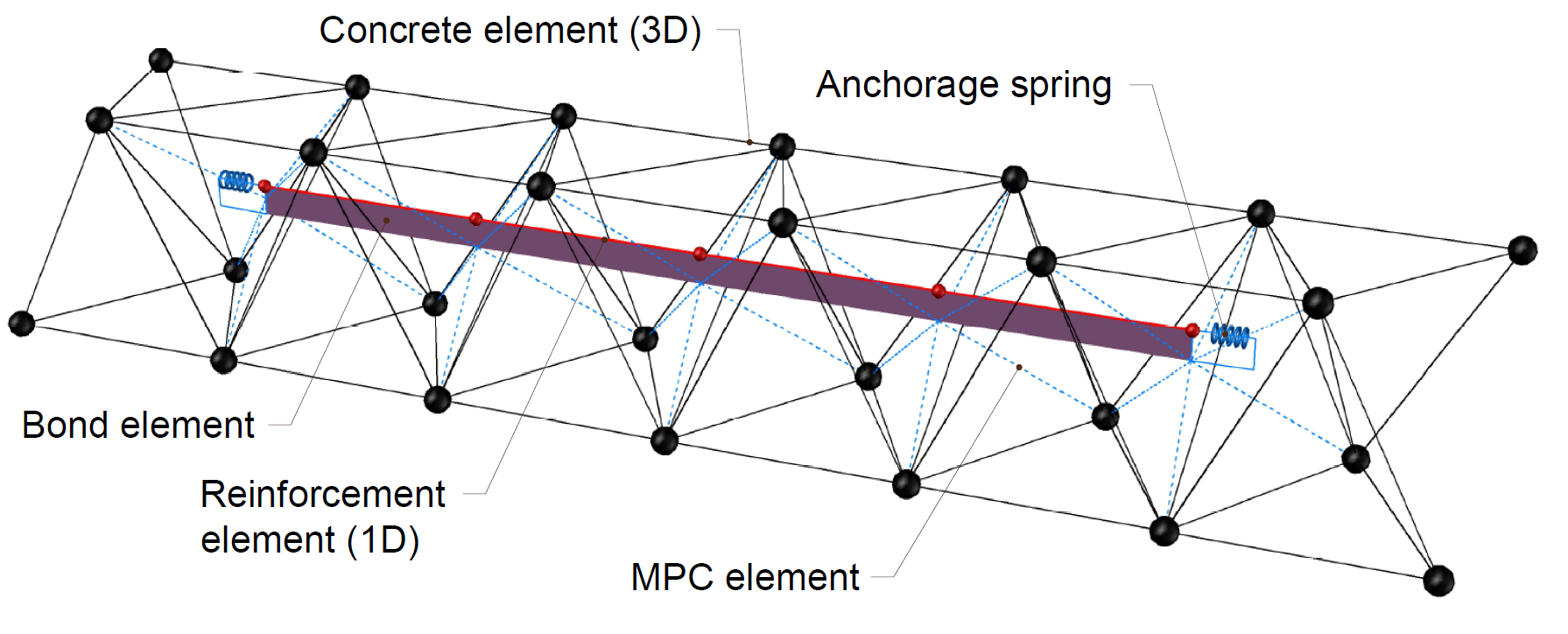
The non-linear (inelastic) finite element analysis model is created by several types of finite elements used to model concrete, reinforcement, and the bond between them. Concrete and reinforcement elements are first meshed independently and then interconnected using multi-point constraints (MPC elements). This allows the reinforcement to occupy any position not limited to nodes of tetrahedral mesh. To verify anchorage length, bond, and anchorage end spring elements are inserted between the reinforcement and the MPC elements.
\[ \textsf{\textit{\footnotesize{Fig. 10\qquad Finite element model: reinforcement elements mapped to concrete mesh using MPC and bond elements}}}\]
Concrete
Concrete is analyzed using mixed tetrahedral elements with nodal rotations. The tetrahedral elements allow us to mesh regions of any topology while the implemented formulation guarantees accurate deformation results (without spurious shear stress known as the shear lock effect) even for the coarse mesh which would not be suitable for linear tetrahedral elements formulation.
Full integration is utilized. It means that each element is equipped with four integration points situated within the volume. Such an integration yields a precise strain and stress field, allowing for sufficient evaluation and presentation of the results across the whole volume. Subsequently, the stop criteria are established based on the value in the integration point.
Reinforcement
Rebars are modeled by two-node 1D “rod” elements (CROD), which only have axial stiffness. These elements are connected to special “bond” elements that were developed in order to model the slip behavior between a reinforcing bar and the surrounding concrete. These bond elements are subsequently connected by MPC (multi-point constraint) elements to the mesh representing the concrete. This approach allows the independent meshing of reinforcement and concrete, while their interconnection is ensured later.
Bond elements
The anchorage length is verified by implementing the bond shear stresses between concrete elements (3D) and reinforcing bar elements (1D) in the finite element model. For this purpose, the “bond” finite element type was developed.
The bond element is defined as a shell finite element connected to elements representing reinforcement by the first layer and by the second layer to concrete mesh via multi-point constraints (MPC elements). It should be noted that the bond element is always displayed in this article with a non-zero height, which is, however, defined as infinitesimal in the model.
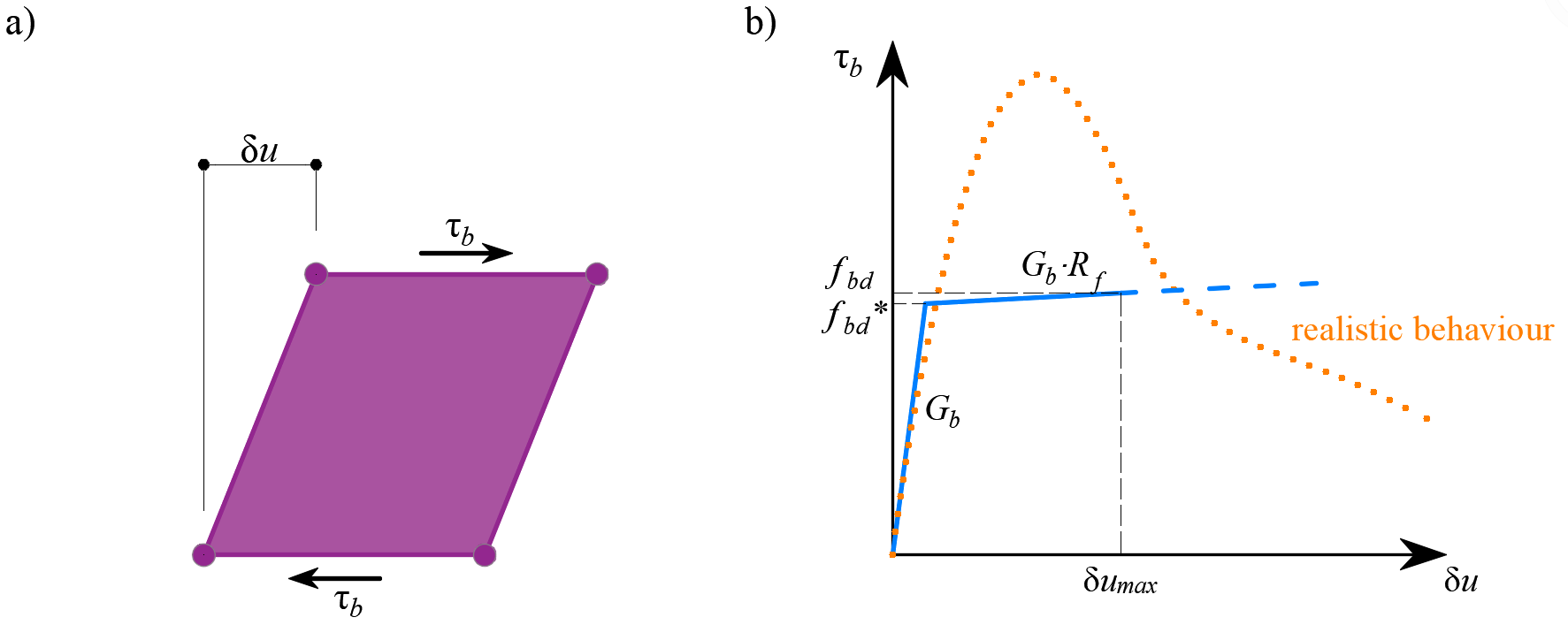
The behavior of this element is described by the bond stress, τb, as a bilinear function of the slip between the upper and lower nodes, δu, see (Fig. 11).
\[ \textsf{\textit{\footnotesize{Fig. 11\qquad (a) Conceptual illustration of the deformation of a bond element; (b) shear-deformation function}}}\]
The elastic stiffness modulus of the bond-slip relationship, Gb, is defined as follows:
\[G_b = k_g \cdot \frac{E_c}{Ø}\]
kg coefficient depending on the reinforcing bar surface (by default kg = 0.2)
Ec modulus of elasticity of concrete (taken as Ecm in case of EN)
Ø the diameter of the reinforcing bar
The design values (factored values) of ultimate bond shear stress, fbd, provided in the respective selected design codes EN 1992-1-1 or ACI 318-19 are used to verify the anchorage length. The hardening of the plastic branch is calculated by default as Gb/105.
Anchorage spring
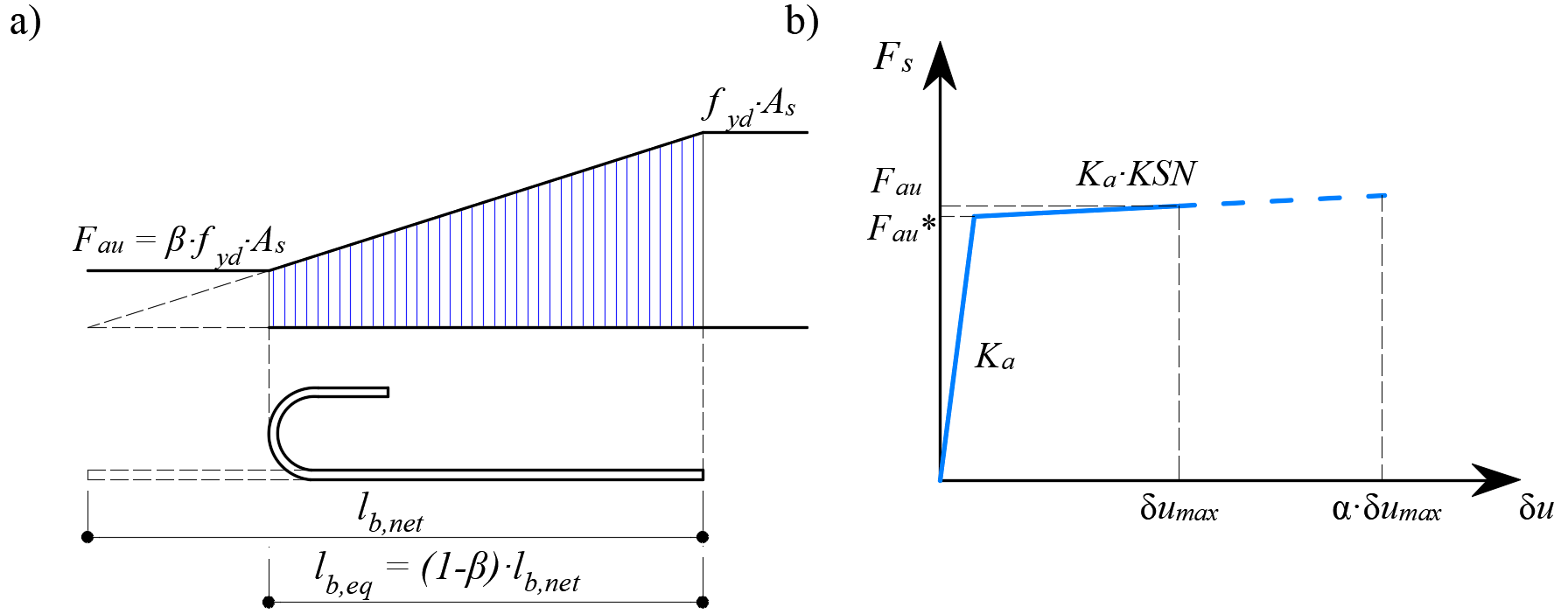
The provision of anchorage ends to the reinforcing bars (i.e., bends, hooks, loops…), which fulfills the prescriptions of design codes, allows the reduction of the basic anchorage length of the bars (lb,net) by a certain factor β (referred to as the ‘anchorage coefficient’ below). The design value of the anchorage length (lb) is then calculated as follows:
\[ \textsf{\textit{\footnotesize{Fig. 12\qquad Model for the reduction of the anchorage length: a) Anchorage force along the anchorage length of }}}\] \[ \textsf{\textit{\footnotesize{the reinforcement bar, b) slip-anchorage force constitutive law}}}\]
The reduction of the anchorage length is included in the finite element model by means of a spring element at the end of the bar (Fig. 12a), which is defined by the constitutive model shown in (Fig. 12b). The maximum force transmitted by this spring (Fau) is:
\[F_{au} = \beta \cdot A_s \cdot f_{yd}\]
where :
β the anchorage coefficient based on anchorage type
As the cross-section of the reinforcing bar
fyd the design value (factored value) of the yield strength of the reinforcement