Materiálově a geometricky nelineární analýza štíhlých mostních prvků v IDEA StatiCa Member

Úvod

Projektanti mostních konstrukcí v často navrhují štíhlé železobetonové pilíře. Důvody jsou tlak na úsporu stavebních materiálů, architektonické požadavky, ale také konstrukční nutnost. Navrhují se například integrované spodní stavby, kde jsou pilíře rámově spojeny s nosnou konstrukcí nebo jsou spojeny prostřednictvím vrubového kloubu. Vzhledem k podélným deformačním účinkům (dotvarování, smrštění, změny teploty, brzdné síly) je pak projektant nucen hledat kompromisní dimenze, kdy spodní stavba musí být dostatečně „měkká“, aby absorbovala vnucené deformace a současně dostatečně tuhá, aby zajistila podélnou stabilitu mostní konstrukce.

Z výše zmíněných důvodů vzniká pro projektanty mostů potřeba nástroje pro přesnější analýzu a posouzení štíhlých tlačených prvků, které jsou citlivé na ztrátu stability a účinky druhého řádu, místo zjednodušených normových metod. Použití této metody umožňuje realističtěji modelovat působení železobetonových prvků, jejichž tuhost se mění vznikem trhlin. Mimo jiné tak umožňuje vyhnout se konzervativním návrhům pomocí běžných metod.

Návrh štíhlých tlačených železobetonových prvků je obtížná problematika, kde je nutné zohlednit následující:

• Geometricky nelineární chování prvku (II. řád)
• Počáteční geometrickou imperfekci
• Materiálovou nelinearitu:

                Nelineární pracovní diagram betonu v tlaku

                Tahové trhliny v betonu

                Dotvarování betonu v čase

Obr. 1 Štíhlý tlačený prut

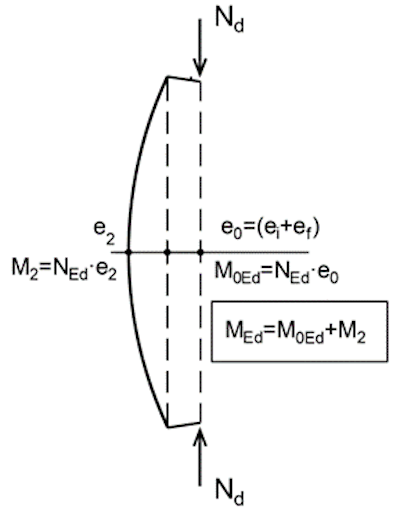
Podstata řešeného problému, v pojetí Eurokódu EN 1992-1-1 Navrhování betonových konstrukcí, je znázorněna na obrázku výše. Na štíhlý, kloubově uložený prut působí síla N_d s počáteční výstředností 

e_o = e_i + e_f

kde  

e_i  je výstřednost vyjadřující počáteční imperfekci

e_f  je výstřednost síly N_d, neboli výstřednost od průběhu ohybových momentů prvního řádu na prvku

Ohybový moment M_oEd uprostřed délky se nazývá moment prvního řádu s účinky imperfekcí a platí

M_oEd = N_d (e_i + e_f)

Příčná deformace prutu e₂ vyvolá moment druhého řádu M₂. Celkový ohybový moment v polovině rozpětí je potom 

M_Ed = M_0Ed + M₂ = N_d (e_i + e_f + e₂)

Ve stanovení excentricity druhého řádu e₂ s respektováním výše popsaných efektů potom leží podstata analýzy a návrhu štíhlých tlačených prutů.

Přehled normových metod

Nejprve uveďme stručný přehled a popis metod pro posouzení štíhlých železobetonových konstrukcí s vlivem druhého řádu, které jsou uvedeny v normě EN 19912-1-1.

Metoda nominální tuhosti – kapitola 5.8.7

Úloha se převádí na náhradní prut a podstatou metody je definování redukované jmenovité tuhosti prutu, která má zohledňovat účinek trhlin, materiálové nelinearity a dotvarování. Celkový moment se potom stanoví pomocí vztahů z teorie pro lineárně pružný tlačený prutu s vlivem II. řádu.

Metoda jmenovité křivosti – kapitola 5.8.8

Odezva tlačeného prvku se řeší pomocí náhradního štíhlého prutu – svislý prut vetknutý v patě a na horním konci volný. Deformace ve vrcholu prutu (tudíž účinek II. řádu v patě) se stanovuje na základě přibližného předpokladu, že přetvoření ve vrcholu prutu (účinek druhého řádu) je funkcí křivosti ve vetknutí náhradního prutu. Na zjednodušujících předpokladů o rovině přetvoření (křivosti) tohoto průřezu se potom odvozuje účinek II. řádu v mezním stavu. Metoda je vhodná pro izolované prvky.

Je zřejmé, že zjednodušené metody jsou (a musí být) festival kompromisů. Výhody zjednodušených metod jsou:

• Jednoduchost. Metody jsou vhodné pro ruční výpočet.
• Konzervativnost a tím zajištěná bezpečnost. Cílem je bezpečný návrh i za cenu vzdálení se od reálného působení prvku.

Hlavní nevýhody zjednodušených metod jsou potom:

• Konzervativnost, která může vést k nehospodárnému návrhu, nebo nemožnosti napasovat metodu na konkrétní statický systém.
• Pracuje se s ekvivalentním ohybovým momentem, nikoliv se skutečným průběhem namáhání po délce, který určuje „potrhání“ průřezu prvku a tím rozložení tuhosti po délce.
• Nerespektují změnu vyztužení po délce prvku.
• Neumožňují analyzovat prvky s proměnným průřezem. 

Obecná nelineární metoda – kapitola 5.8.6

Obecná metoda je založena na analýze zahrnující materiálovou i geometrickou nelinearitu. Norma nedefinuje přesně způsob analýzy, ale definuje principy a předpoklady, které musí být zohledněny. V tomto článku prezentovaná metoda a programový nástroj pro geometricky a materiálově nelineární analýzu s imperfekcí (GMNIA) pak spadá mezi tyto obecné metody a je v souladu s požadavky normy.

Geometricky a materiálově nelineární analýza s počáteční imperfekcí - GMNIA

GMNIA je implementována v programu IDEA StatiCa Member. Jedná se o nástroj pro analýzu prutových ŽB prvků a konstrukcí pomocí metody konečných prvků. Podstata a inovativnost metody je založena na formulaci prutového konečného prvku.

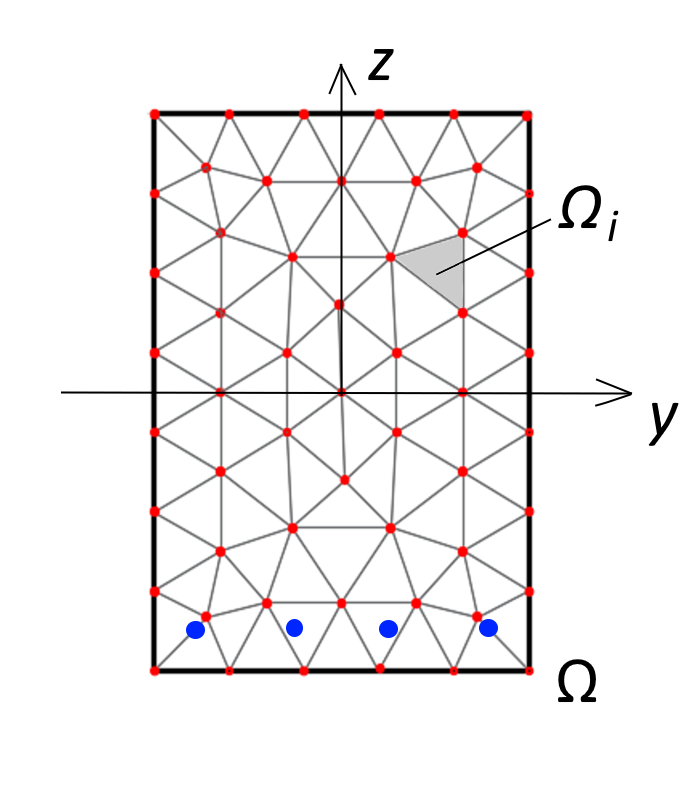
Obr. 2: Příčný řez prutového konečného prvku

Příčný řez prvku je schematicky znázorněn na obr. 2. Průřez, reprezentovaný oblastí Ω, se rozdělí na síť 2D plošných prvků, každý prvek s dílčí oblastí Ω_i. Tvar průřezu může být zcela libovolný a podstata modelu spočívá v tom, že každá podoblast a výztuž (Obr. 2 vyznačeno šedě) může obecně reprezentovat libovolný materiál s vlastním nelineárním pracovním diagramem. V našem případě má beton nelineární pracovní diagram v talku a vyloučeno působení v tahu. Výztuž má pružno-plastický diagram v talku i tahu. Princip metody je pak založen na přímé integraci vnitřních sil po průřezu (oblasti Ω). V rámci iterace nelineárního MKP výpočtu jsou nejprve stanovena uzlová přemístění, na základě kterých je vypočten průběh poměrných přetvoření po průřezu. Normálová napětí v jednotlivých podoblastech Ω_i jsou pak vypočtena z těchto poměrných přetvoření na základě nelineárních pracovních diagramů jednotlivých materiálů přiřazených podoblastem. Přímou integrací po průřezu se následně určí přenesené vnitřní síly a ty se porovnají s aplikovanými silami. Pokud jsou splněna kritéria konvergence, následuje výpočet dalšího kroku nelineárního výpočtu s dalším přírůstkem zatížení. Přičemž během jednotlivých kroků výpočtu se aktualizuje matice tuhosti konstrukce dle aktuálního stavu napjatosti a tím „potrhání“ průřezu. Pro nelineární výpočet je použita Newton-Raphsonova iterační metoda. Použitý konečný prvek je podrobněji popsán v práci [4], verifikace metody je popsána v příspěvku [3]. 

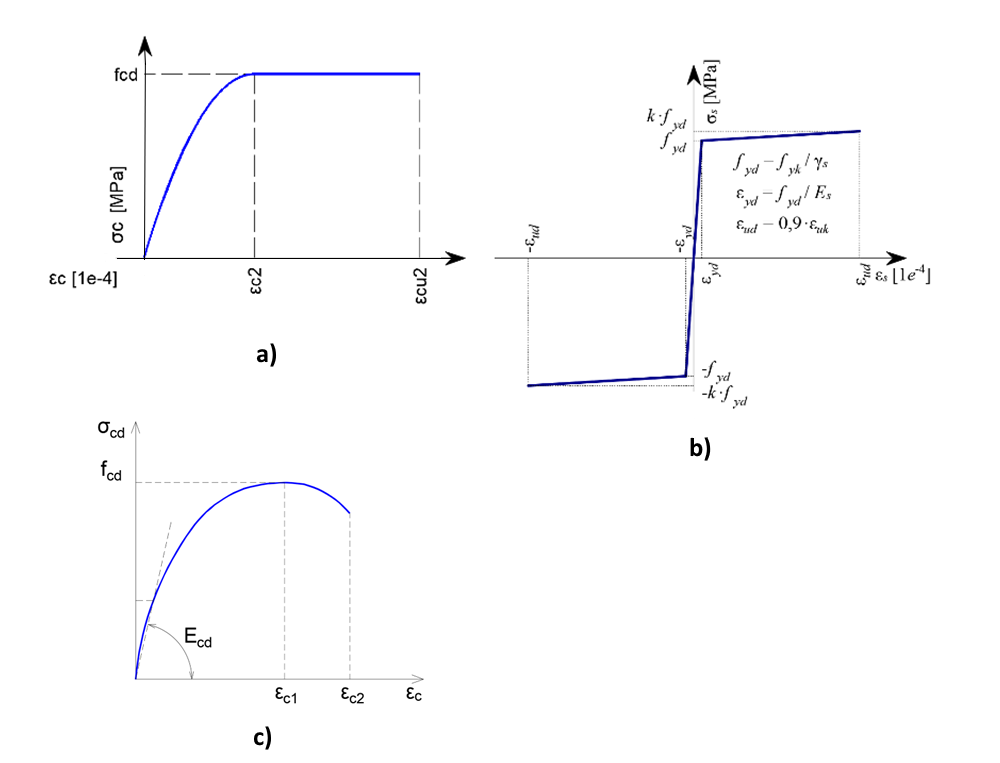
Obr. 3: Pracovní diagramy materiálů a) tlačený beton, b) výztuž, c) pracovní diagram pro nelineární analýzu dle EN 1992-1-1

Výpočet mezní únosnosti se provádí s návrhovými hodnotami vlastností materiálů a s návrhovými hodnotami zatížení. Formát spolehlivosti je tak v souladu s předpoklady eurokódu EN 1992-1-1. V programu je pro beton v tlaku implementován standartní parabolicko-rektangulární pracovní diagram pro posouzení průřezů z normy. Norma definuje také obecnější návrhový pracovní diagram pro nelineární analýzu konstrukcí (obr. 3c). Použití pracovního diagramu pro průřezy je konzervativní, s implementací obecného pracovního diagramu se počítá v dalším vývoji programu. Uvažovaný bilineární pracovní diagram výztuže opět vychází z normy a je uveden na obr. 3b. 

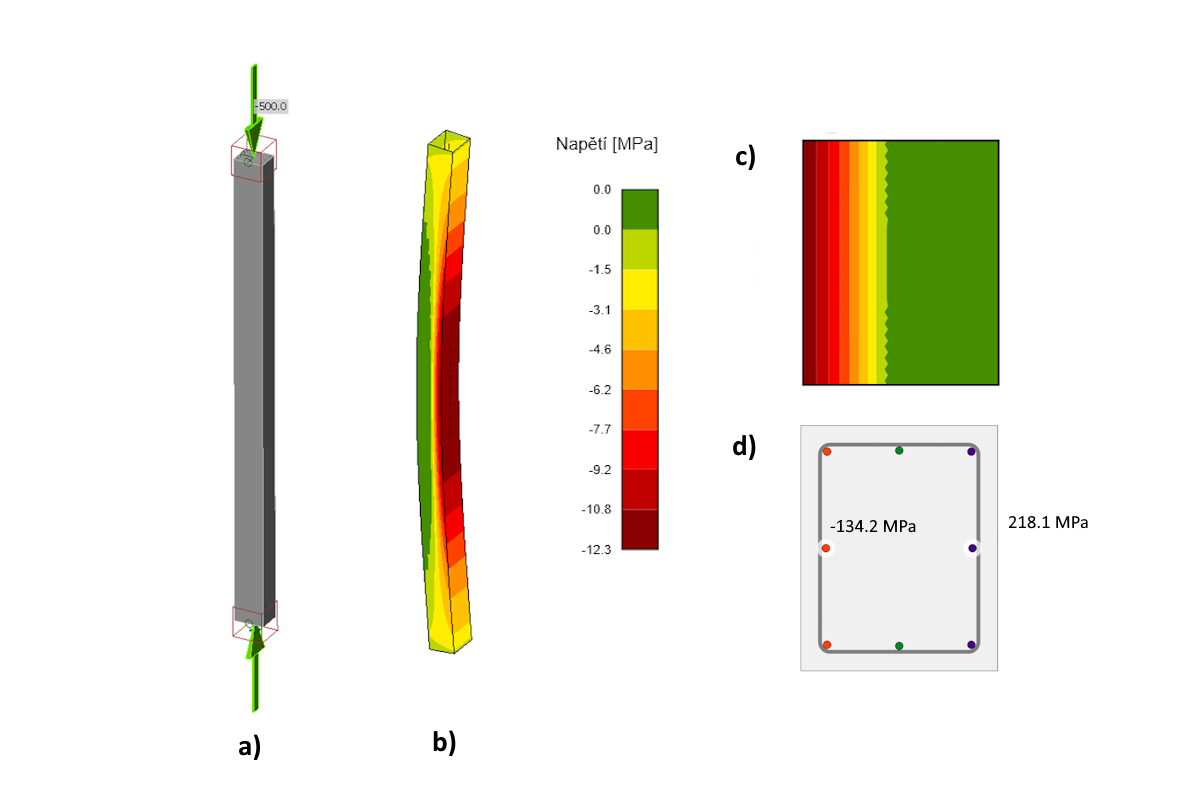
Doplněním výše popsané materiálově nelineární analýzy na prutovém modelu o geometrickou nelinearitu a možnost definovat počáteční geometrickou imperfekci dostáváme obecnou metodu pro geometricky nelineární analýzu s počáteční imperfekcí – GMNIA. Výstupem výpočtu je pole tlakových napětí v betonu (obr. 4b, c) a napjatost ve výztuži (obr. 4d). Pokud během výpočtu dojde od aplikovaných návrhových zatížení k překročení mezních přetvoření betonu, výztuže nebo ztrátě stability prvku (viz. dále), program automaticky iteračně vypočte maximální hladinu zatížení. 

 Obr. 4: Posouzení obdélníkového sloupu a) geometrie, b) napětí na prutu po délce, zelená oblast – vyloučený beton v tahu, c) napětí v betonu v kritickém řezu, d) napětí ve výztuži v kritickém řezu

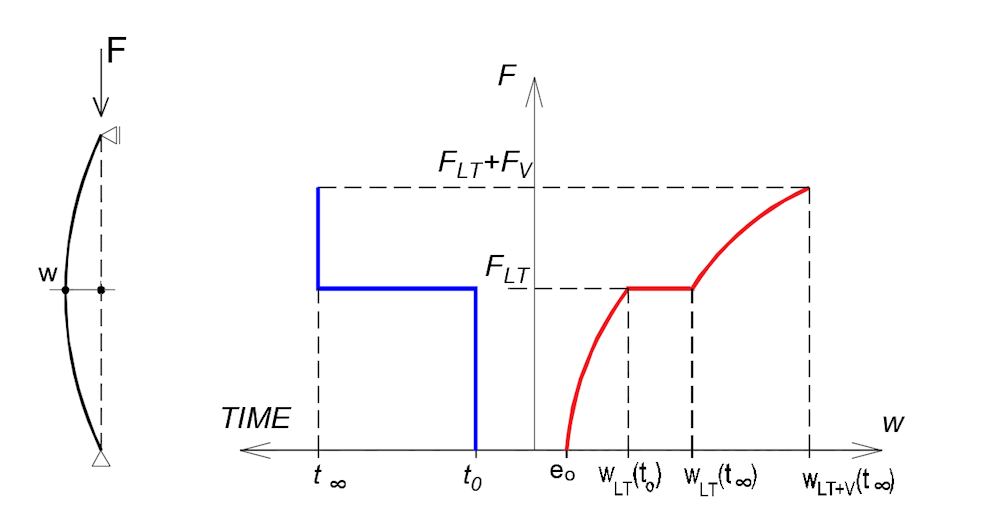
Jak již bylo zmíněno na začátku kapitoly 1, zásadní pro odezvu štíhlých tlačených ŽB prvků je také zohlednění vlivu dotvarování tlačeného betonu. Princip vlivu dotvarování na chování tlačeného prvku je znázorněn na obr. 5. Předpokládejme, že celková působící síla F se stává z dlouhodobé složky F_LT a krátkodobé složky F_V. Síla F_LT vyvodí v čase t₀ příčnou deformaci w_LT(t₀). Tato deformace (resp. excentricita síly) se skládá z počáteční imperfekce a deformace od vlivu II. řádu. V čase dojde vlivem dotvarování betonu k nárůstu deformace w_LT(t₀) na hodnotu w_LT(t_∞). Přičemž nárůst příčné deformace vlivem dotvarování způsobí v čase samozřejmě i nárůst deformace II. řádu. Je zjevné, že se jedná o komplexní chování a pro jeho přesný popis by byl nutný výpočet pomocí časově závislé analýzy (TDA). To program Member v současnosti neumožňuje. Je nutné efekt dotvarování zahrnout do výpočtu manuálně tak, že k počáteční geometrické imperfekci se přičte hodnota příčné deformace, která je vyvolána dotvarováním. Tu je nutné stanovit manuálně pomocí součinitele dotvarování. Postup je popsán detailněji v tomto článku.

Obr. 5 Vývoj příčné deformace tlačeného železobetonového prvku v čase

Postup posouzení tlačeného prvku v programu Member je potom následující:

1. Zadání konstrukce, okrajových podmínek, vyztužení a zatížení
2. Materiálově nelineární výpočet MNA
3. Výpočet tvarů boulení pomocí LBA (linear buckling analysis). Tvar boulení se použije pro zadání průběhu geometrické imperfekce po délce prutu. 
4. Definování počáteční geometrické imperfekce a to včetně nárůstu příčné deformace v čase vlivem dotvarování.
5. Finální posouzení pomocí GMNIA 

Příklad použití programu Member – štíhlá kyvná stojka

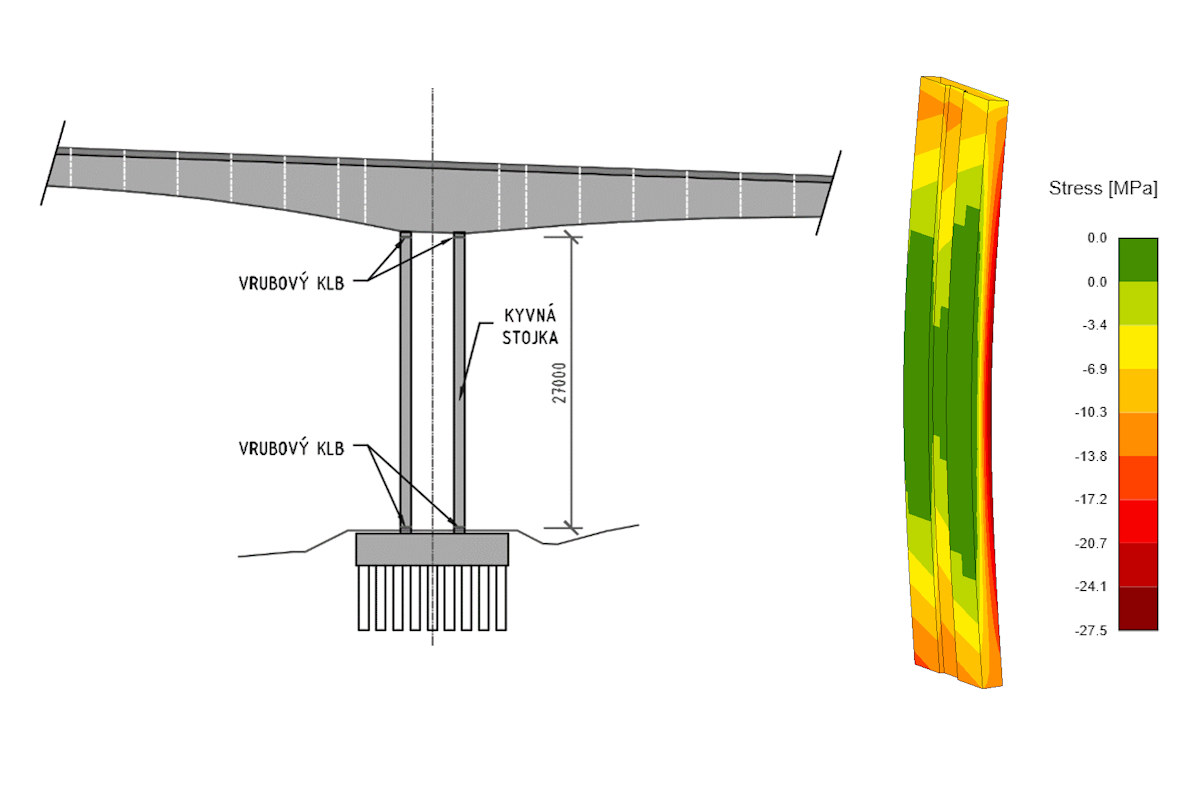
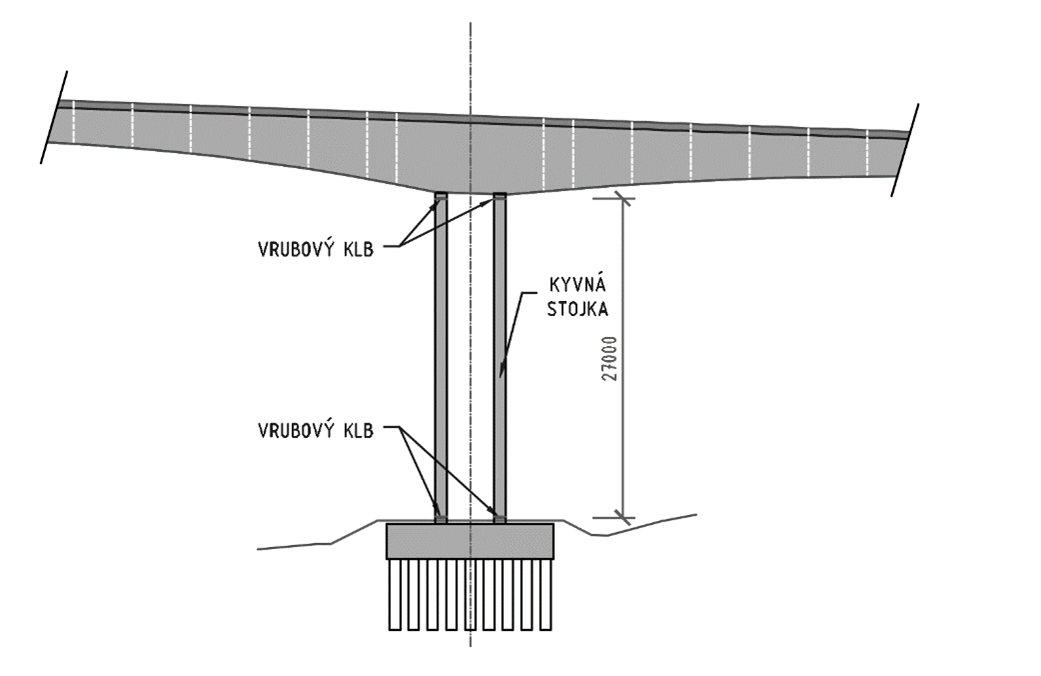
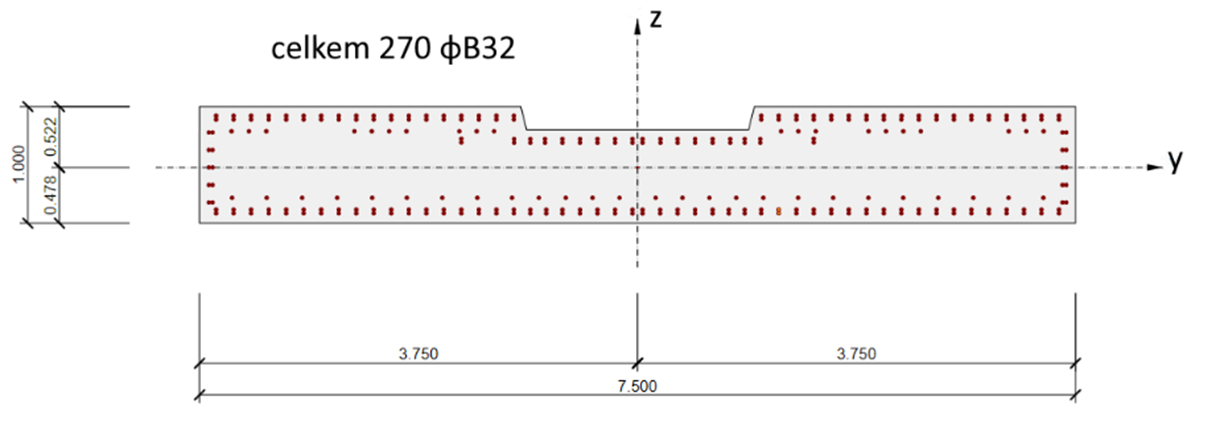
Rozdíl mezi jednotlivými návrhovými přístupy bude ukázán na příkladu posouzení štíhlého silně vyztuženého prvku z reálné konstrukce. Na obr. 6 je schematický podélný řez vahadla letmo betonovaného mostu. Spodní stavbu tvoří dvojice velmi štíhlých stojek, které mají nad základem a pod nosnou konstrukcí vrubové klouby. Průřez těchto kyvných stojek tvoří obdélník rozměru 7,50 x 1,0 m s vybráním. Vzdálenost vrubových kloubů je 27,0 m. Štíhlost stojky je λ = 97. Příčný řez stojek je silně vyztužen, celkem 270 vložek φB32 (obr. 7), beton stojky je třídy C50/60.

Obr. 6 Podélný řez

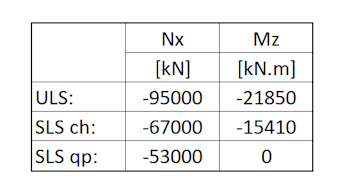
Síly a momenty působící v úrovni horního vrubového kloubu je uvedeny v tabulce 1. Vedle těchto sil bylo v kombinaci pro posouzení dále uvažováno zatížení podélným větrem.

Tab. 1 – Zatížení v hlavě stojky

Obr. 7 Příčný řez kyvnou stojkou

Počáteční geometrická imperfekce stojky byla uvažována e_o(t_o) = 45mm. Celková počáteční imperfekce zahrnující vliv nárůstu příčného průhybu vlivem dotvarování byla stanovena iteračním výpočtem pomocí GMNIA a součinitele dotvarování na e_o(t_∞) = 105 mm. Součinitel dotvarování byl uvažován φ(t_∞,t_o) = 2.0.

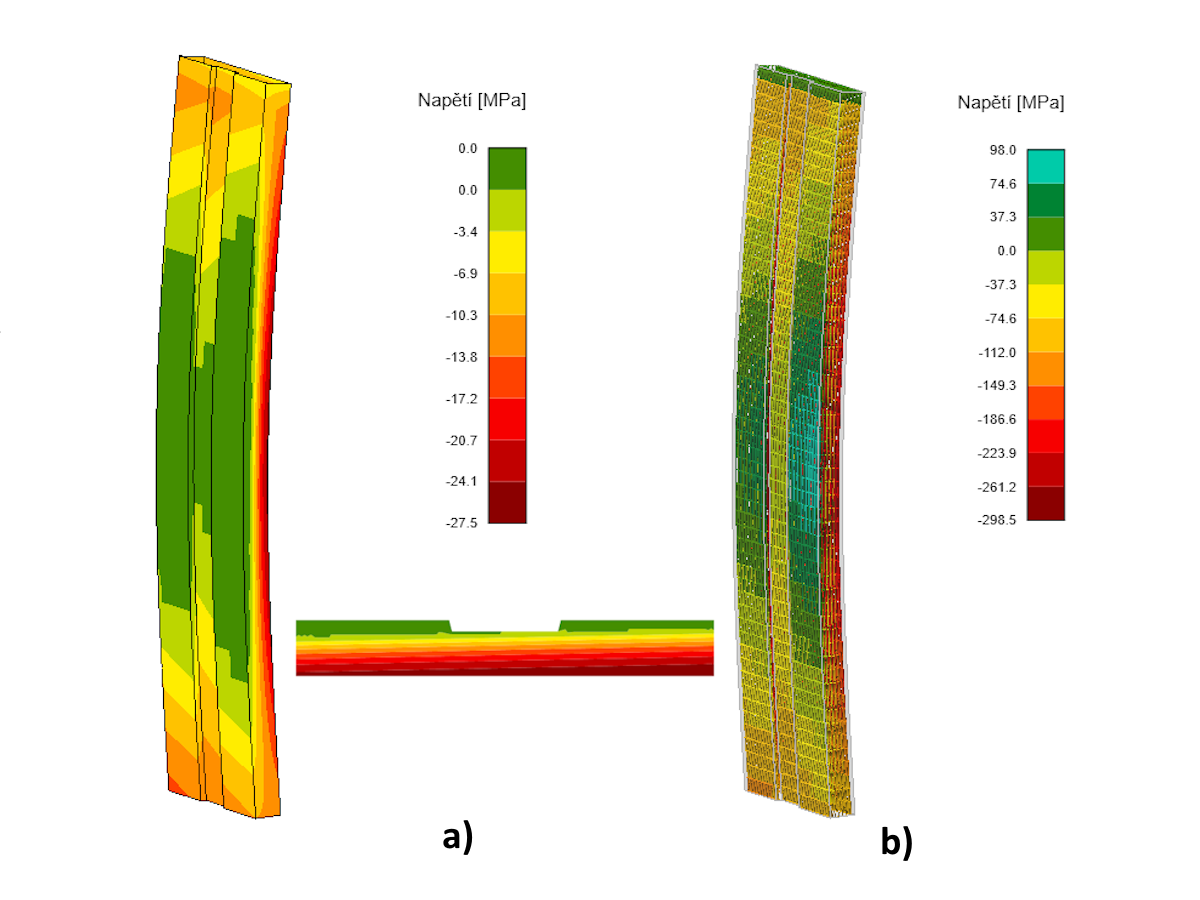
Obr. 8 Napětí na stojce pro N_Ed = -112 300 kN a) napětí v betonu, zelená oblast – vyloučený beton v tahu b) napětí v podélné výztuži

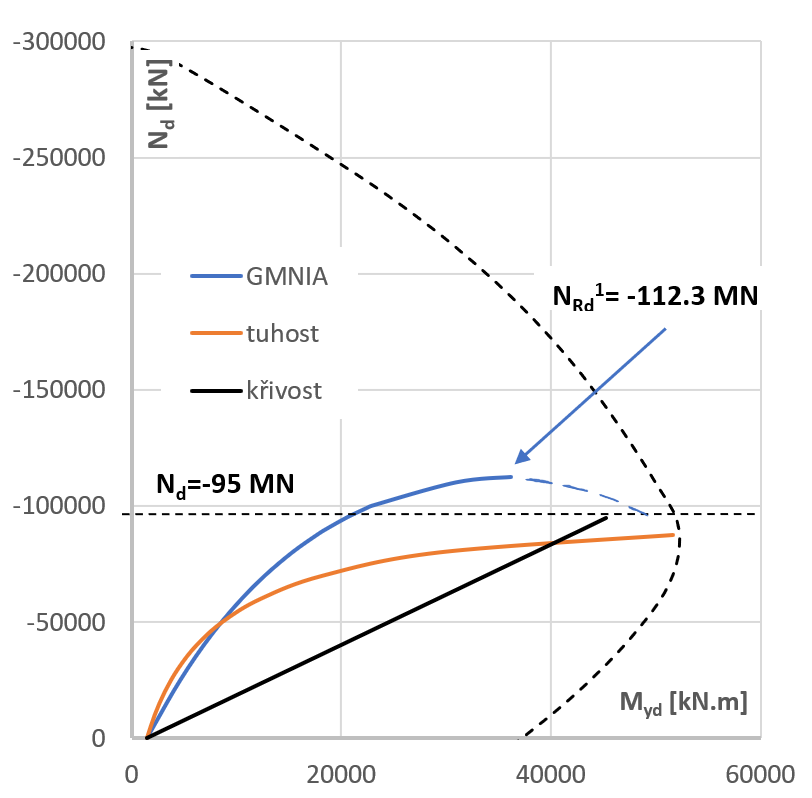
Výsledky posouzení stojky v ULS a porovnání s ostatními přístupy jsou uvedeny na obrázcích 8 a 9. Pro názornost jsou výsledky analýzy dokumentovány pomocí interakčního diagramu N-M_y pro průřez uprostřed stojky. Mezní únosnost byla hledána postupným zvyšováním normálové síly při zachování ostatních zatížení a počáteční geometrické imperfekce. V grafu je pak zobrazen postupný nárůst celkového ohybového momentu M_y,Ed pomocí jednotlivých metod. 

Mezní únosnost stojky byla pomocí GMNIA stanovena na N_Rd1= -112 300 kN. Křivka nárůstu M_y,Ed má nelineární průběh, jak se postupně zvyšují účinky druhého řádu. Mezní únosnosti je dosaženo ztrátou stability stojky (viz následující odstavec). Únosnost je vyšší než N_Ed = -95 000 kN, stojka tedy vyhověla. Napětí v betonu pro návrhovou sílu N_Ed jsou ukázána na obr. 8. Z obrázku je zřejmá část objemu stojky (zelená barva), kde je vyloučeno působení betonu v tahu. 

Chování stojky odpovídá ztrátě stability. I když nebylo dosaženo mezního stavu průřezu, tlačený prvek již není schopen při zachování rovnováhy sil na přetvořené konstrukci přenášet větší normálovou sílu. Kdyby byla použita metoda pro nelineární výpočet sestupné větve po dosažení mezní síly (např. Arc length method), křivka by pokračovala sestupnou větví a tam, kde by protnula interakční diagram a došlo by k porušení průřezu. Pro výše popsaný způsob porušení ztrátou stability, který je typický pro velmi štíhlé prvky, je nutné doplnit následují komentář. Hladina spolehlivosti konstrukce je při návrhu podle Eurokódu zajištěna na straně zatížení součinitelem zatížení, na straně materiálu dílčími součiniteli spolehlivosti materiálu, které redukují pevnost betonu a výztuže. Při výše popsaném způsobu porušení (ztráta stability) se však součinitele materiálu nedostanou „ke slovu“ a hlavním materiálovým parametrem, který definuje mezní nosnost je pak modul pružnosti betonu. Při posuzování velmi štíhlých prvků tak musí inženýr pečlivě vážit jaké materiálové parametry vstupují do výpočtu a hlavně zajistit, že předpokládaný modul pružnosti bude dosažen i na reálné konstrukci.

Obr. 9 Interakční diagram N, My

Na obr. 9 je dále dokumentováno posouzení pomocí metody jmenovité tuhosti. Křivka reprezentující nárůst ohybového momentu M_y,Ed při zvětšování normálové síly protne interakční diagram a je dosaženo mezní únosnosti průřezu. Průsečíku odpovídá mezní normálová síla N_Rd2 = -87 500 kN. Stojka tedy nevyhověla. Lze konstatovat, že tvar křivky u této metody odpovídá chování štíhlého železobetonového tlačeného prvku.

Metodou jmenovité křivosti stanovený celkový ohybový moment M_y,Ed pro návrhovou sílu N_Ed je uvnitř plochy interakčního diagramu a stojka při použití této metody tedy vyhověla. Z průběhu nárůstu ohybového momentu MEd je vidět, že v tomto případě je průběh téměř lineární. Je vidět, že metoda vychází ze zjednodušeného předpokladu o stavu rozhodujícího průřezu v mezním stavu a nevystihuje tak vůbec postupný nárůst účinků druhého řádu při zvyšování tlakové normálové síly.

Závěr

Z uvedeného příkladu je zřejmé, že zjednodušené normové metody se ve výsledcích poměrně zásadně liší. Obě jsou konzervativní a mohou vést k nehospodárnému návrhu. Použití GMNIA umožňuje věrněji vystihnout skutečné působení prvku. 

Možnosti programu IDEA StatiCa Member byly prezentovány na příkladu velmi štíhlé kyvné stojky. Vývoj programu bude dále pokračovat tak, aby umožnil řešit širokou množinu konstrukčních uspořádání spodních staveb mostních konstrukcí. Cílem je vyvinout nástroj pro inženýrskou praxi v souladu s návrhovou normou, nikoliv vědecký nástroj pro nelineární analýzu skutečné odezvy konstrukce na působící zatížení.

Popsaná metoda je samozřejmě vhodná nejen pro návrh štíhlých tlačených prvků, ale i pro analýzu železobetonových nosníků nebo rámů, kdy ve výpočtovém modelu dochází automaticky k redistribuci vnitřních sil vlivem potrhání průřezů.

Literatura

[1] FILLO L., BENKO V., DOBRÝ J.: Reliability of Slender Reinforced Concrete Columns in Second Generation of Eurocodes. Solid State Phenomena Vol:309. p. 228-233., 2020.

[2] EN 1992-1-1 (2004) Design of concrete structures. Part: 1-1 General rules and rules for buildings. (2004)

[3] BOBEK, L.; JUŘÍČEK, L.; KOMÁRKOVÁ, P.; KABELÁČ, J.: Verifikace materiálově a geometricky nelineární metody pro návrh a posouzení štíhlých betonových sloupů. 28. Betonářské dny (2022), sborník ke konferenci. Praha: Česká betonářská společnost ČSSI, 2022. ISBN: 978-80-907611-6-2.

[4] KABELÁČ, J., Materiálově nelineární řešení prutových konstrukcí. Brno, 2016. 97 s. Disertační práce. Vysoké učení technické v Brně, Fakulta stavební, Ústav stavební mechaniky. Vedoucí práce doc. Ing. Ivan Němec