Member - okrajové podmínky

_Úvod

IDEA StatiCa Member pracuje s částí konstrukce, která je "odříznuta" od globálního 3D FEM modelu. Program proto nechává definici okrajových podmínek na projektantovi.

V aplikaci IDEA StatiCa Member můžete definovat okrajové podmínky na koncích přípojných prutů. Aplikace nabízí zadání:

a) Podpory - definice podpor by měla odpovídat vašemu 3D FEA modelu

b) Koncové síly na přípojných prutech - odpovídají vnitřním silám vypočteným ve standardním 3D FEM programu

Bez použití podpor nelze zadat pouze koncové síly na přípojných prutech. Používá se zde přesnější model (např. lokální excentricity prutů a zohledňují se skutečné délky prutů). Takto zavedené imperfekce pro analýzu GMNIA způsobují, že rovnováha není zachována, a proto může být definován i mechanismus.

Doporučuje se zadat opodstatněné podpory na základě úsudku stavebního inženýra.

c) Podpory + Koncové síly na přípojných prutech - minimální opodstatněné podpory na základě úsudku statika + přidání vnitřních síl z programu 3D FEM.

Vnitřní síly z globálního modelu

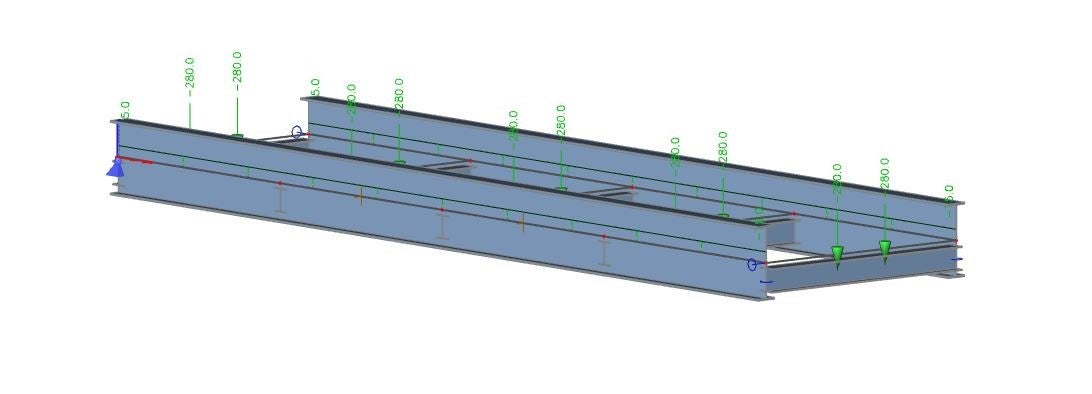
Z globálního modelu je vyříznut segment konstrukce. Výběr řezu je zcela libovolný a závisí na úsudku uživatele. Model by měl být symetrický, což se v tomto případě i projeví.

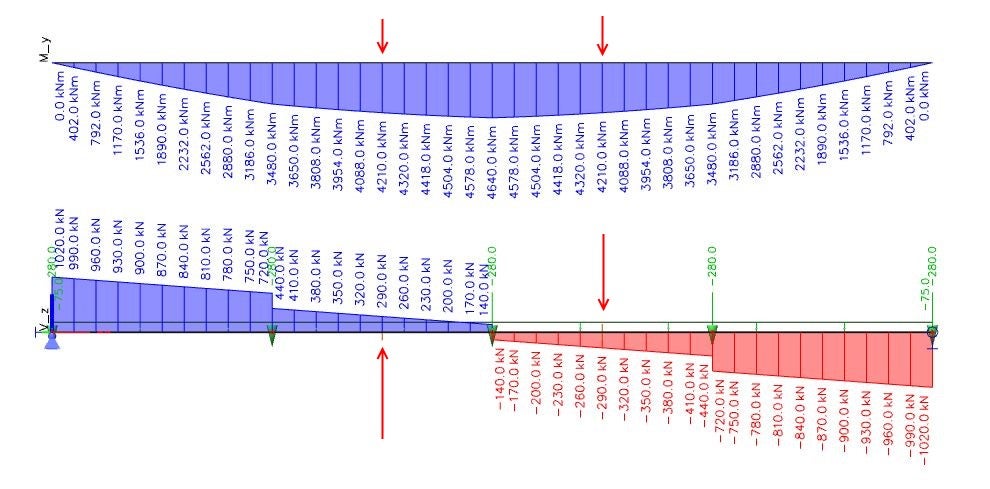
Obr. 01 Ohybové momenty a smykové síly na hlavním nosníku

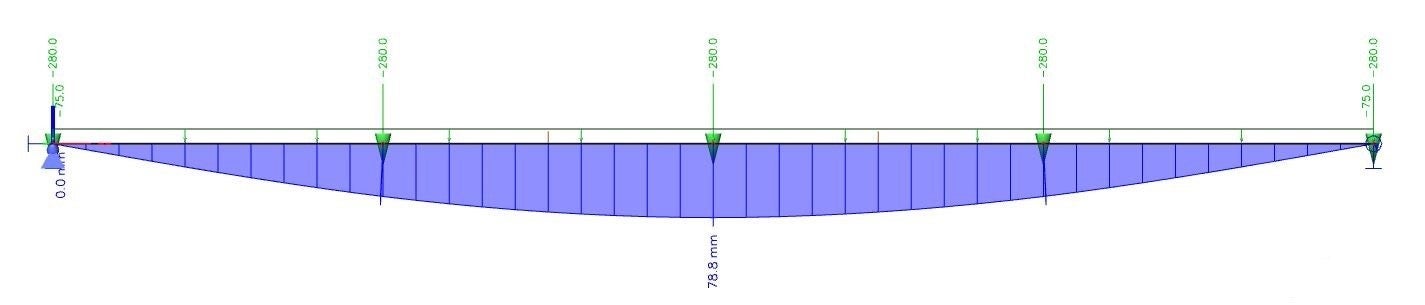
Obr. 02 Globální deformace hlavního nosníku

Obr. 03 Normálové napětí na hlavním nosníku

Vliv okrajových podmínek v IDEA StatiCa Member

Okrajové podmínky mají velký vliv na chování konstrukce. Uživatel by měl při modelování segmentu konstrukce v IDEA StatiCa Member respektovat globální chování konstrukce.

Okrajové podmínky by měly být zvoleny podle chování globálního modelu. Ani posun, ani rotace by neměly být omezeny žádným dalším napětím, které by mohlo vzniknout. Neznalost těchto pravidel má velký vliv na výsledky všech tří dostupných typů analýz: materiálově nelineární analýzy (MNA), lineární analýzy vzpěru (LBA) a geometricky a materiálově nelineární analýzy s imperfekcemi (GMNIA).

Důležitá pravidla jsou uvedena v následujících bodech:

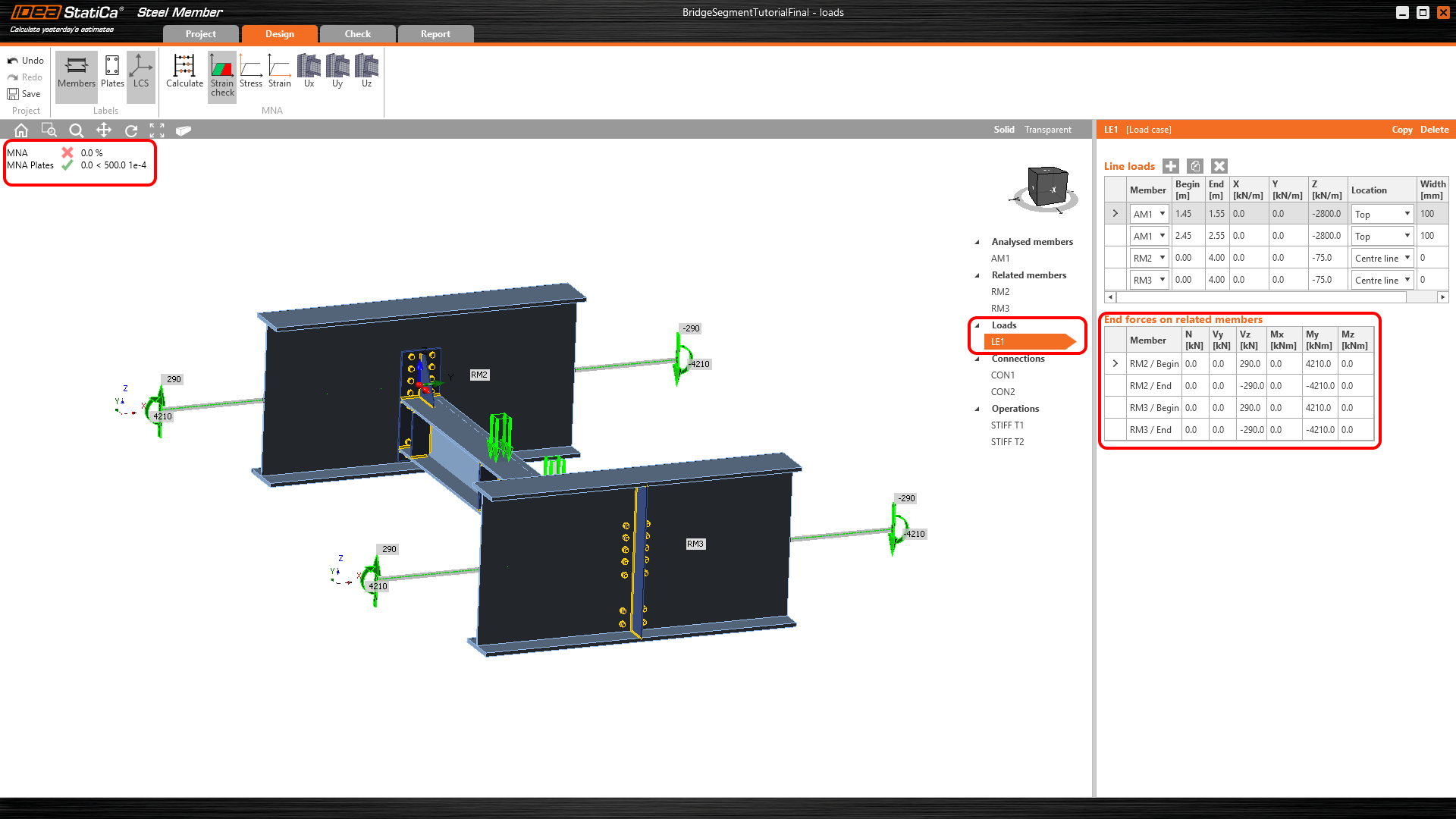
• Model je po exportu v rovnováze, pokud jsou vnitřní síly (N, V, M) zadány na koncích přípojných prutů.
• Okrajové podmínky slouží k omezení dodatečných reakcí, které byly vytvořeny po analýzách MNA, LBA a GMNIA.
• Bez okrajových podmínek nelze model vypočítat.

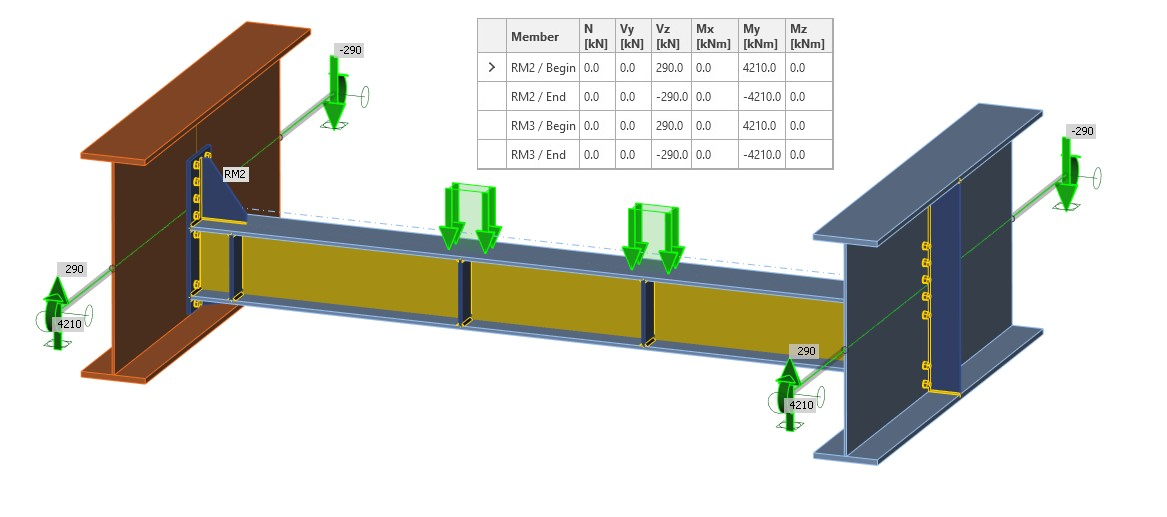
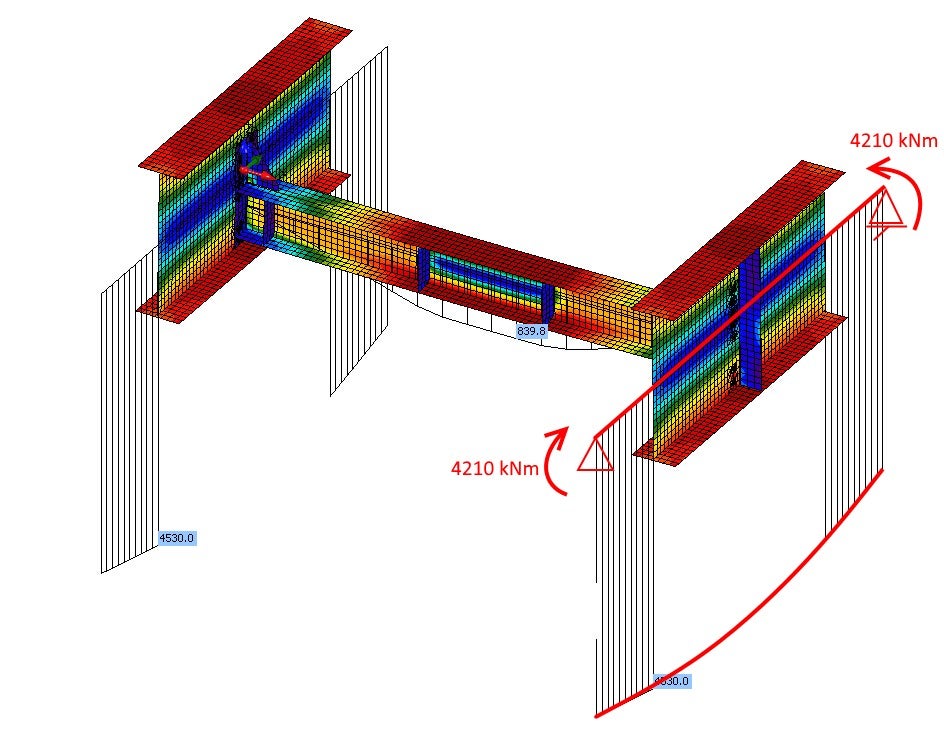
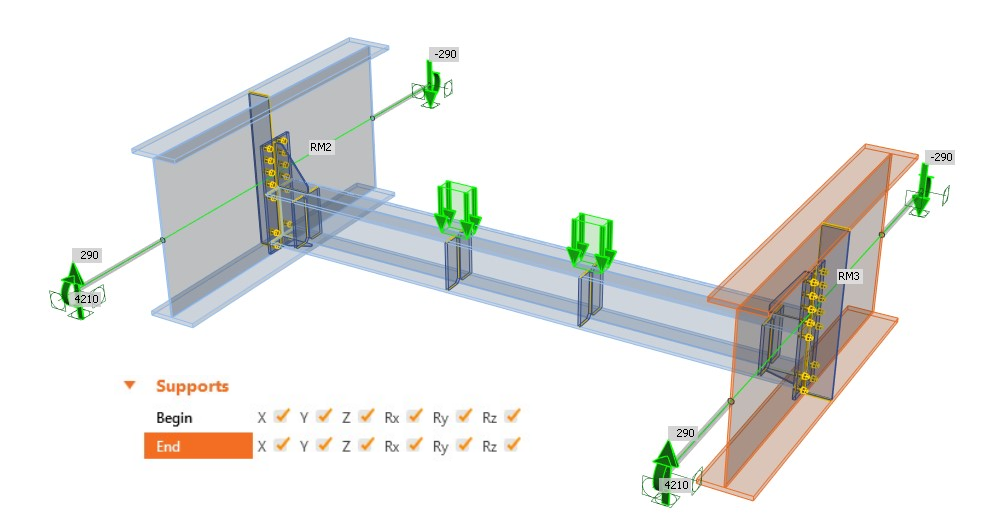
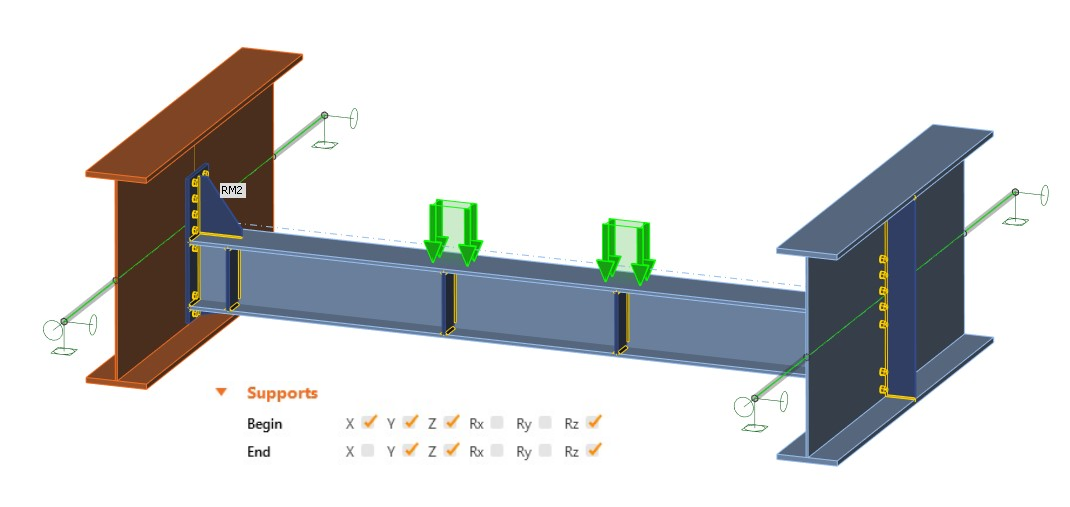
Obr. 04 Vnitřní síly na konci přípojných prutů

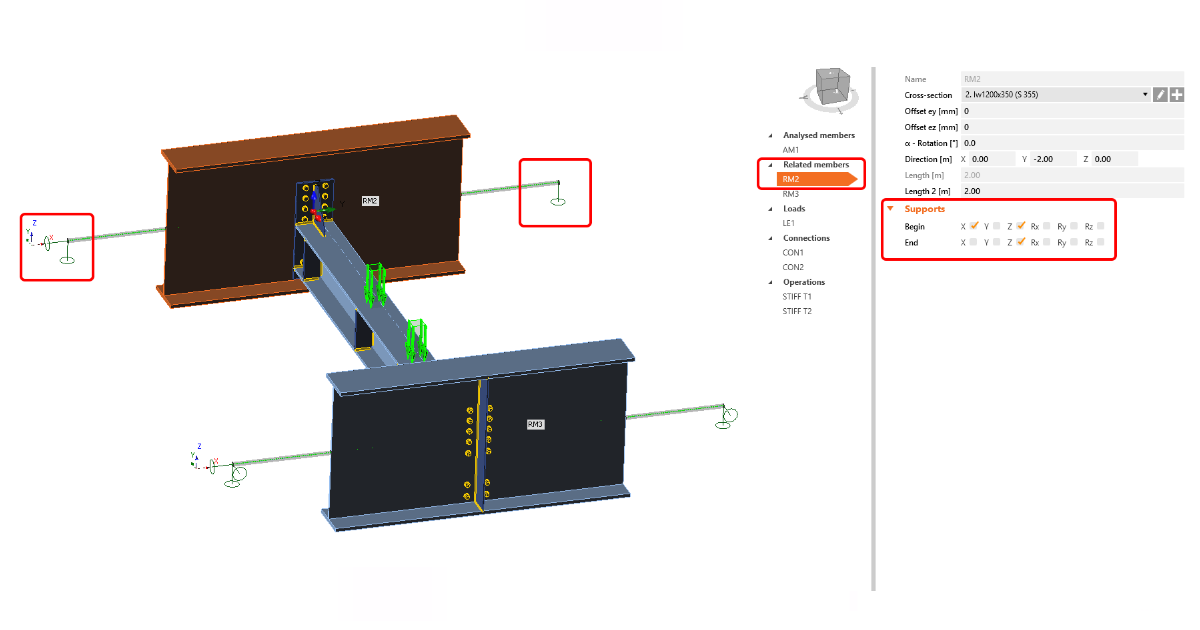
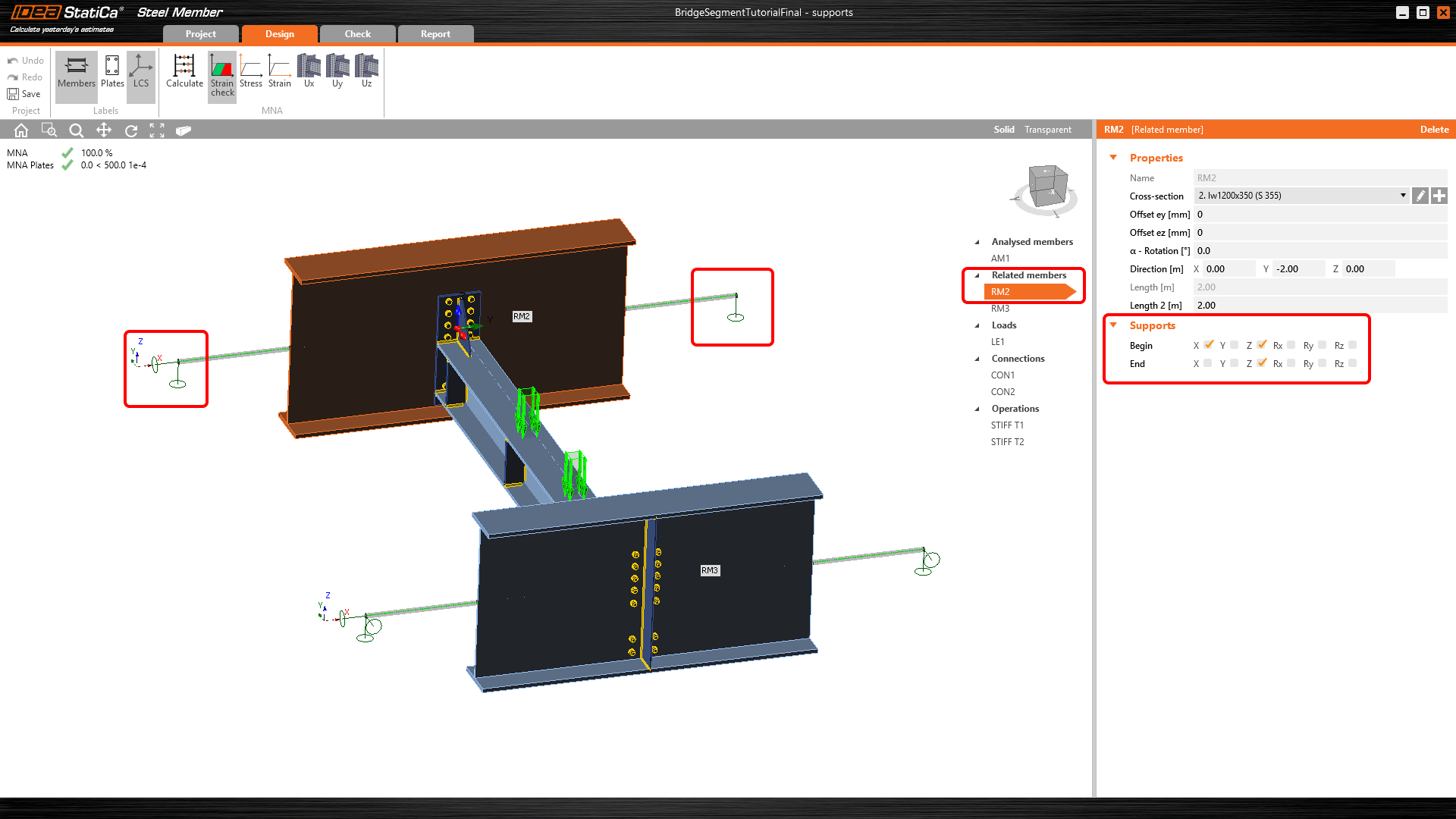
Příklad 1: Správné okrajové podmínky a vnitřní síly na koncích přípojných prutů

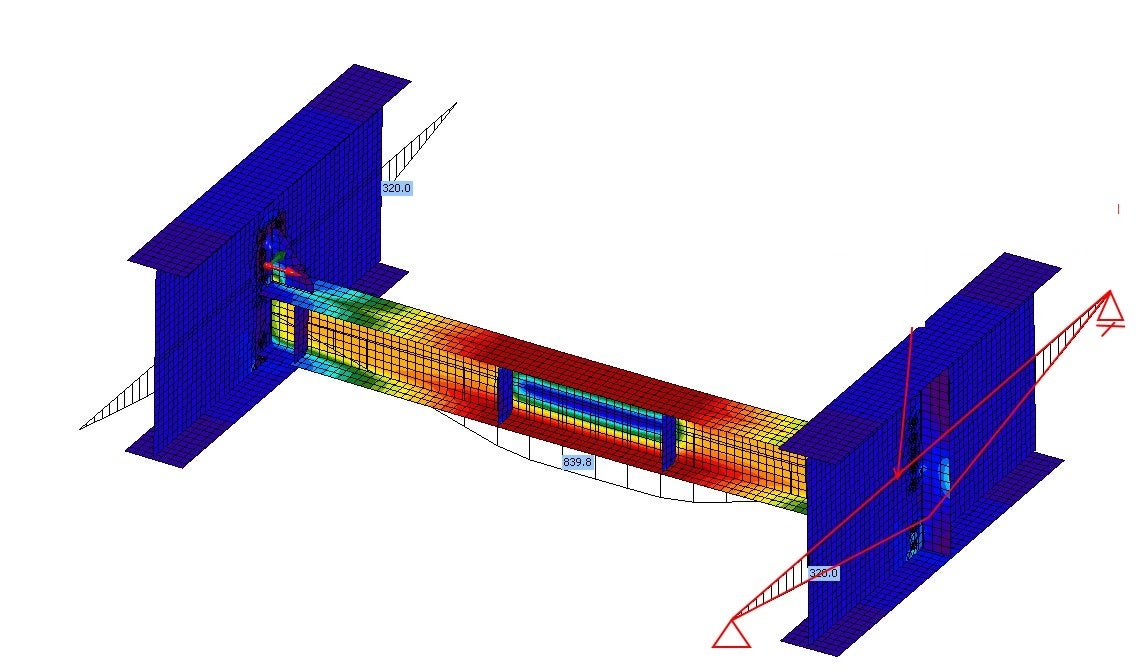
Tento model obsahuje okrajové podmínky odpovídající globálnímu modelu, tj. klouby (obr. 05). Díky vnitřním silám na konci přípojných prutů získáte odpovídající diagram vnitřních sil jako v globálním modelu (obr. 06).

Obr. 05 Klouby a vnitřní síly na konci přípojných prutů

Obr. 06 Ohybové momenty v aplikaci Member

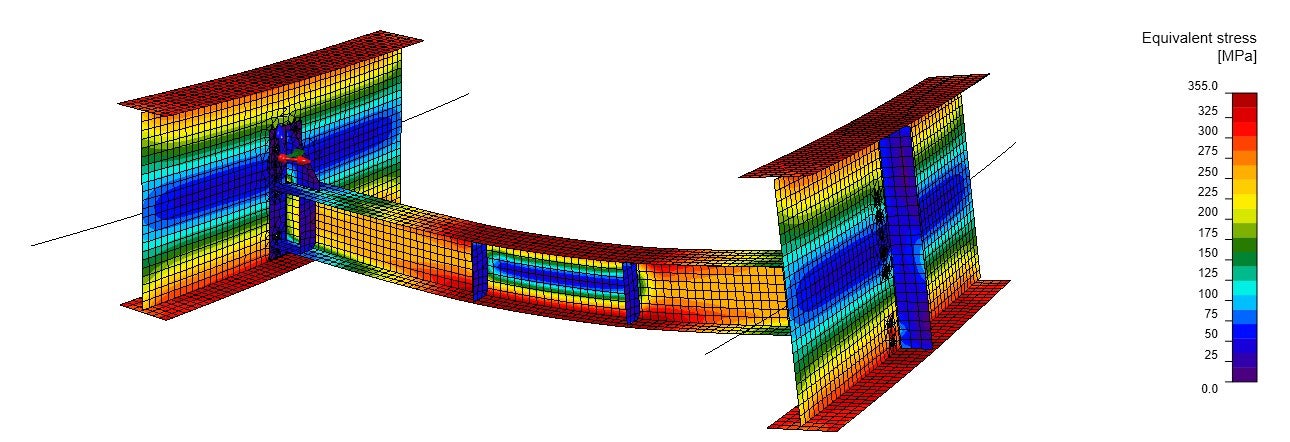
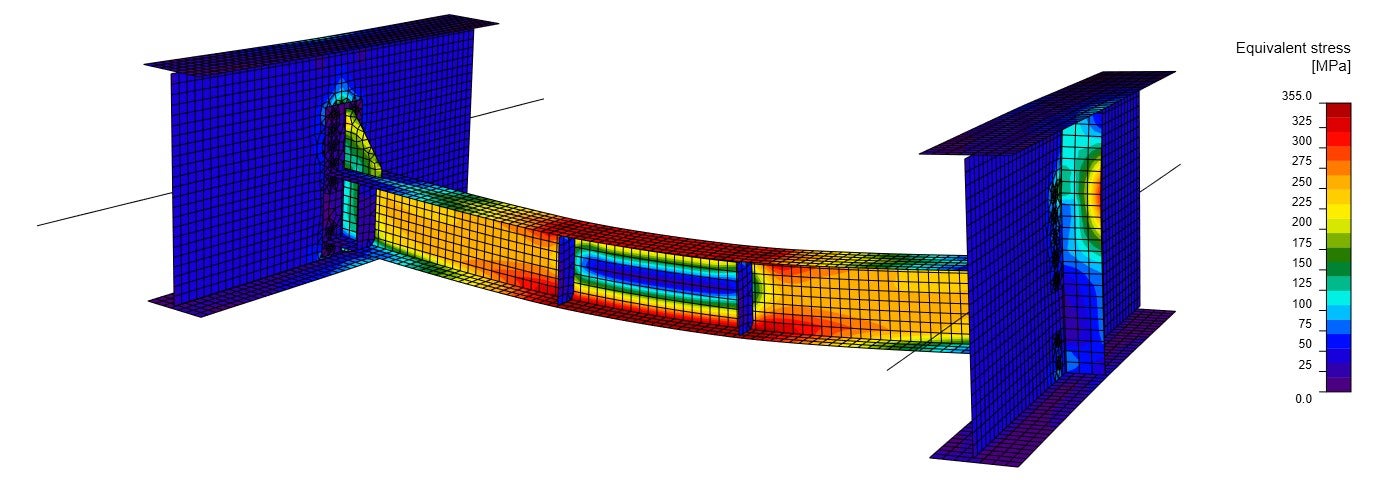
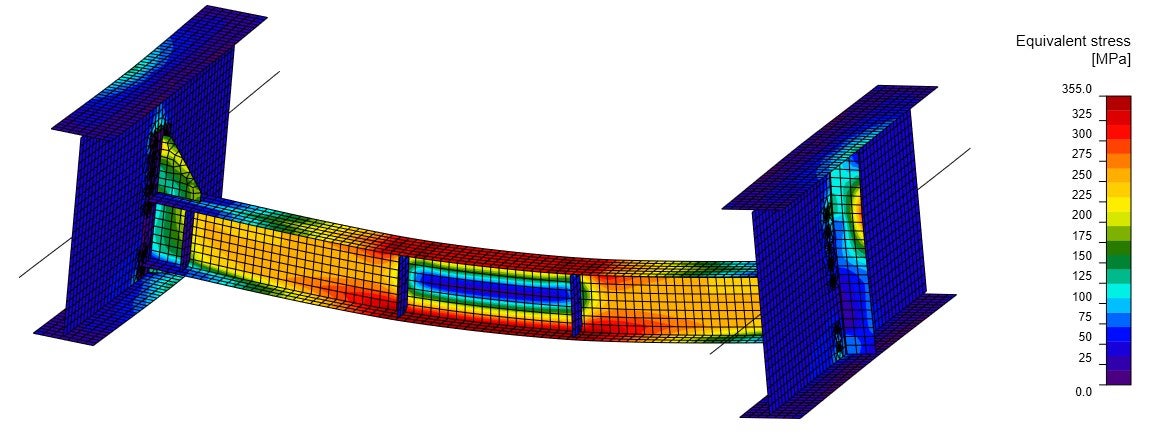
Ekvivalentní napětí a deformace dokazují, že okrajové podmínky a diagram vnitřních sil (obr. 06) odpovídají globálnímu modelu konstrukce (obr. 03). Výsledky ekvivalentního napětí jsou o něco vyšší než v lineární analýze v globálním MKP modelu (obr. 03), a to díky deskovému modelu a zohlednění skutečné tuhosti spojů mezi membránou a hlavními nosníky.

br. 07 Ekvivalentní napětí z materiálově nelineární analýzy

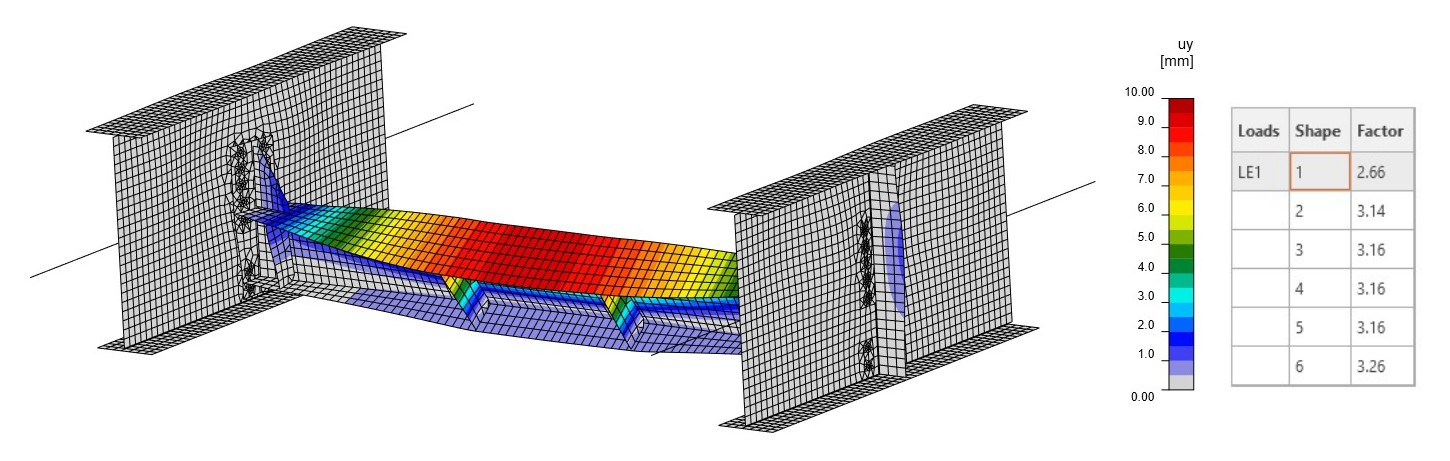
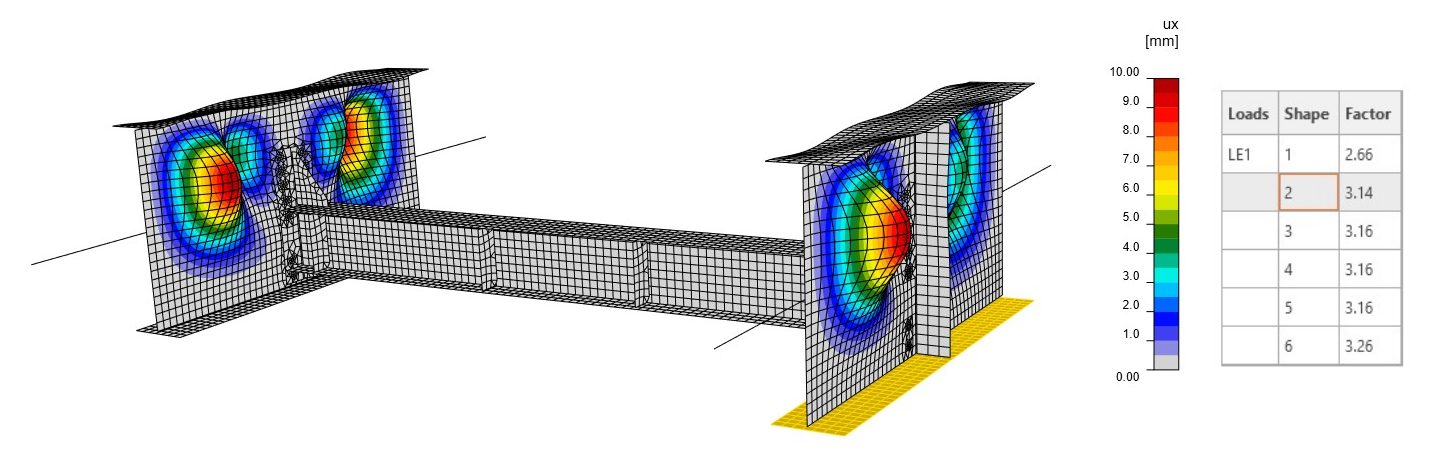
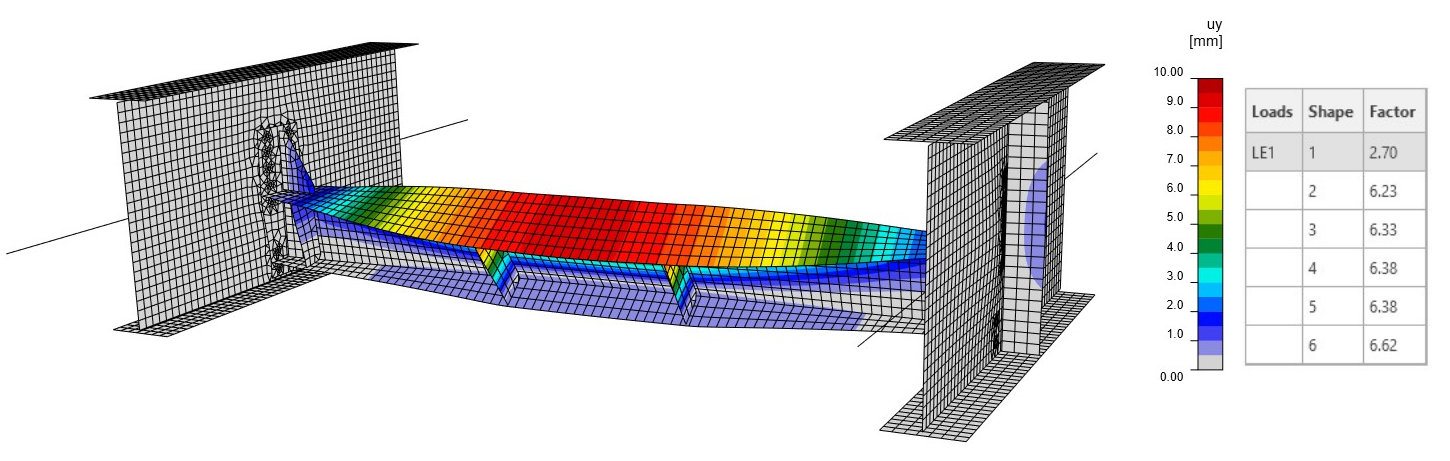
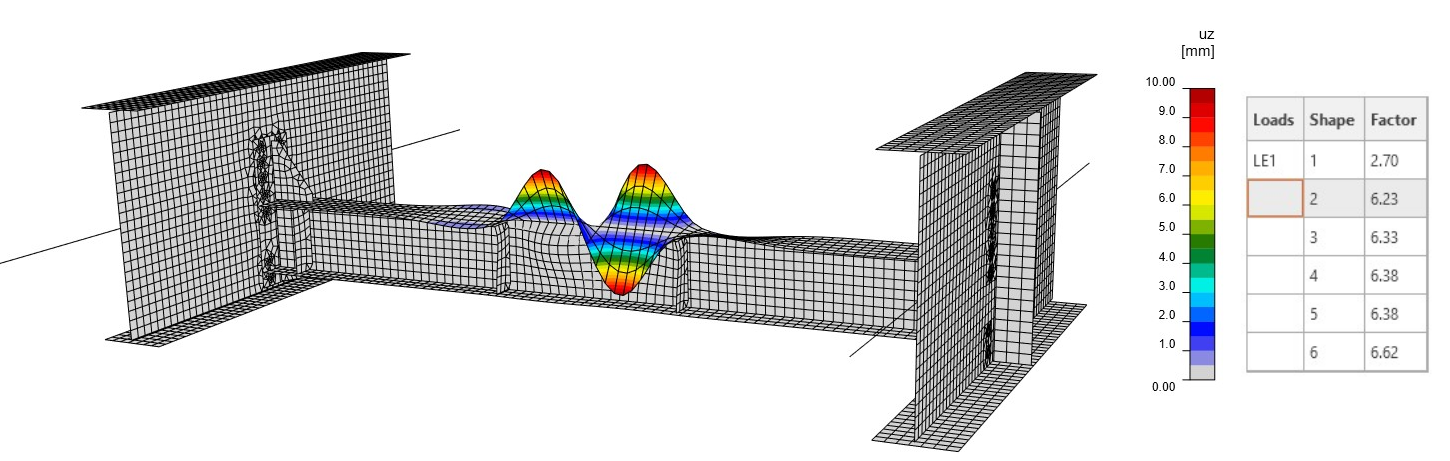
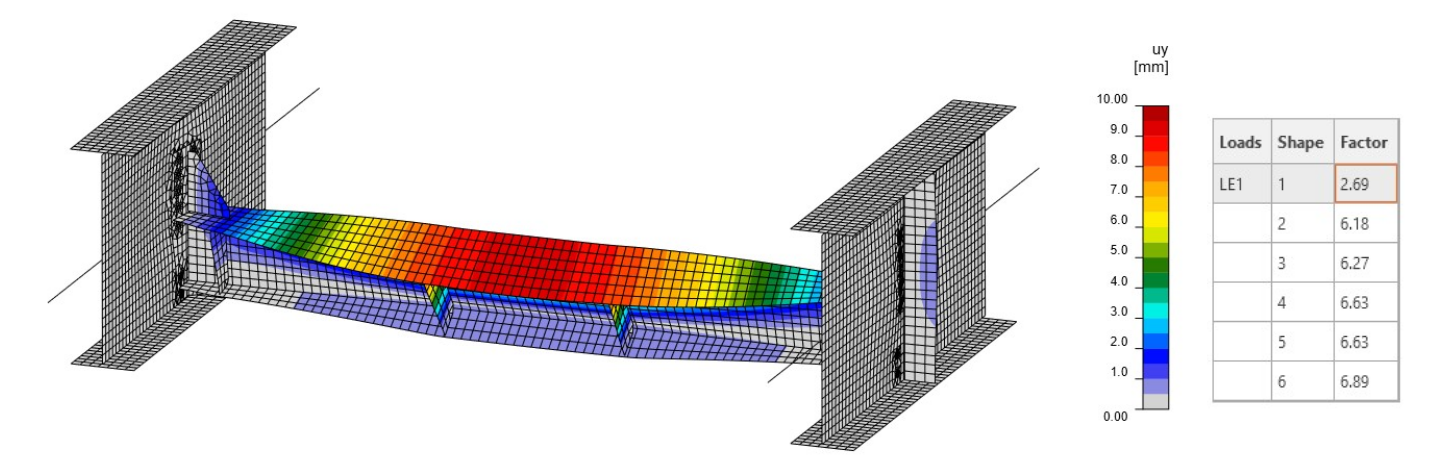
Z lineární analýzy vzpěru (LBA) vyplývá, že první kritický faktor dosahuje hodnoty 2,66. Tvar prvního módu způsobuje boulení membrány (obr. 08). Druhý součinitel je blízký prvnímu a dosahuje hodnoty 3,14 (obr. 09). Tento tvar režimu způsobuje lokální vybočení pásnice hlavního nosníku. Tvar boulení a kritický součinitel jsou ovlivněny tuhostí přípojů, tuhostí hlavních nosníků a také okrajovými podmínkami.

Obr. 08 Tvar prvního módu

Obr. 09 Tvar druhého módu

Příklad 2: Nesprávné okrajové podmínky a vnitřní síly na konci přípojných prutů

Pokud nedodržíme správnost okrajových podmínek (obr. 10) na konci přípojných prutů, dostaneme zcela jiné vnitřní síly (obr. 11). To nám již napovídá, že okrajové podmínky jsou zvoleny nesprávně a vyčleněná část konstrukce se chová jinak než globální model (obr. 01).

Obr. 10 Tuhé okrajové podmínky a vnitřní síly na konci přípojných prutů

Tyto vnitřní síly a napětí jsou zcela odlišné od globálního modelu. Okrajové podmínky mírně ovlivnily i vnitřní síly membrány. (Obr. 11 vs. Obr. 06). V důsledku omezení posunu a rotace (Rx) se přerozdělení vnitřních sil liší od obr. 06.

Obr. 11 Ohybové momenty v aplikaci Member

Obr. 12 Ekvivalentní napětí z materiálově nelineární analýzy

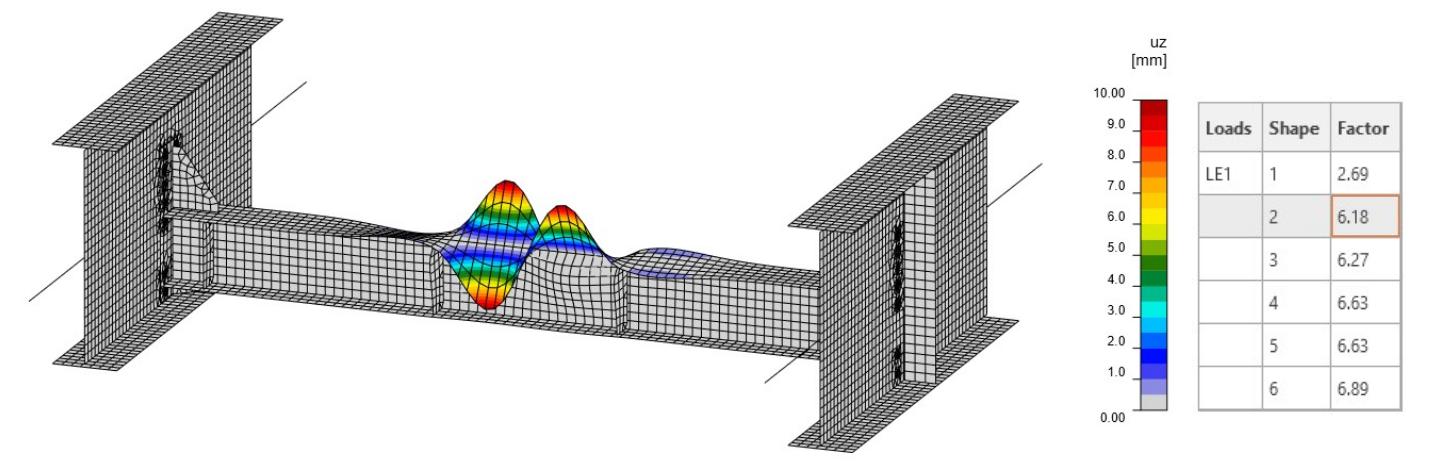
Tvar prvního módu dává ve srovnání s prvním příkladem (obr. 08) o něco vyšší kritický součinitel 2,70 (obr. 13). Tento efekt je způsoben odlišnými okrajovými podmínkami použitými v modelu. Tento tvar režimu představuje boulení membrány, a jak vidíme, napětí a vnitřní síly jsou přibližně stejné jako na obr. 06. To je důvod, proč první tvar vypadá podobně a má téměř stejný součinitel. Okrajové podmínky mají malý vliv na části v daném modelu, které jsou nepřímo spojeny se přípojnými pruty. Naopak druhý tvar (obr. 14) je v porovnání s tvarem na obr. 09 zcela odlišný a jeho kritický součinitel je 6,23. Zde dochází k boulení na horním pásu membrány.

Pokud se podíváme pouze na výsledky LBA, zdá se, že model je správný. Nicméně chování globální konstrukce je zcela odlišné, a proto přístup s takovými okrajovými podmínkami nelze použít.

Obr. 13 Tvar prvního módu

Obr. 14 Tvar druhého módu

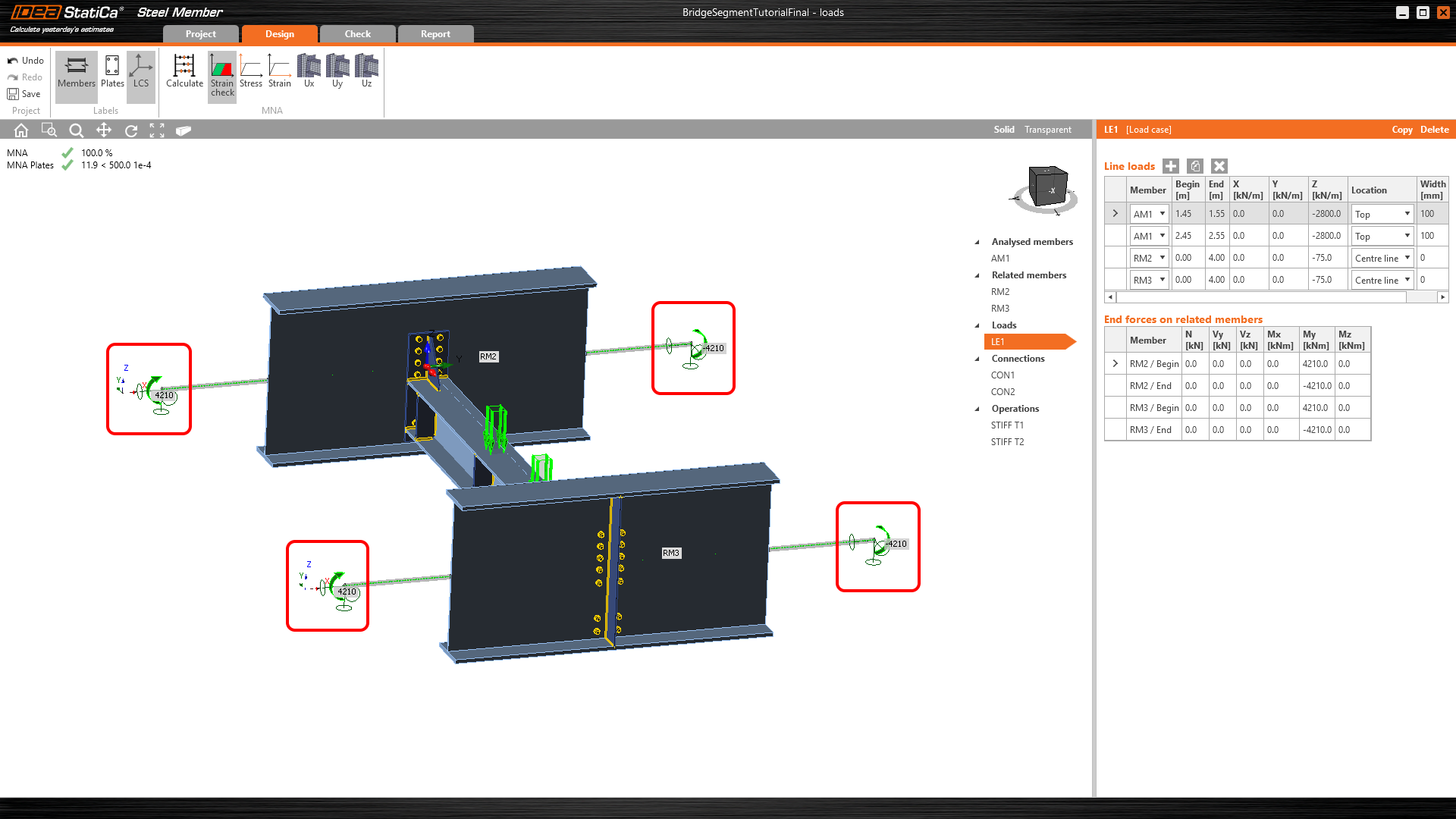
Příklad 3: Správné okrajové podmínky a případné vnitřní síly na konci přípojných prutů

Obr. 15 Klouby a případné vnitřní síly na konci přípojných prutů

Správné okrajové podmínky (odpovídající globálnímu modelu), ale bez zadání vnitřních sil na konci přípojných prutů (obr. 15), způsobují trojúhelníkový tvar ohybových momentů (obr. 16). Z vnitřních sil je patrné, že toto chování není v souladu s chováním globálního modelu. U vnitřních sil u membrány na obr. 16 lze pozorovat jeden zajímavý jev - vnitřní síly jsou stejné jako v modelu v prvním příkladu (obr. 06). Můžeme tedy konstatovat, že pokud jsou správně definovány okrajové podmínky a jsou zadány případné vnitřní síly na konci přípojných prutů, MNA se na nepřímo připojených prutech provede správně.

Obr. 16 Ohybové momenty v aplikaci Member

Obr. 17 Ekvivalentní napětí z materiálově nelineární analýzy

Tvar prvního módu odpovídá prvnímu modelu (obr. 08); můžeme tedy říci, že GMNIA bude provedena správně. Druhý módový tvar je podobný druhému modelu (obr. 14) z důvodu chybějících vnitřních sil na konci přípojných prutů.

Obr. 18 Tvar prvního módu

Obr. 19 Tvar druhého módu

Závěr

• Globální model, deformace segmentu konstrukce a jeho vnitřní síly a napětí jsou vodítkem pro stanovení správných okrajových podmínek.
• Okrajové podmínky ovlivňují chování přípojných prutů.
• I když na konci přípojných prutů nepůsobí vnitřní síly, analýzy MNA, LBA a GMNIA se provedou správně za předpokladu, že byly definovány vhodné okrajové podmínky.