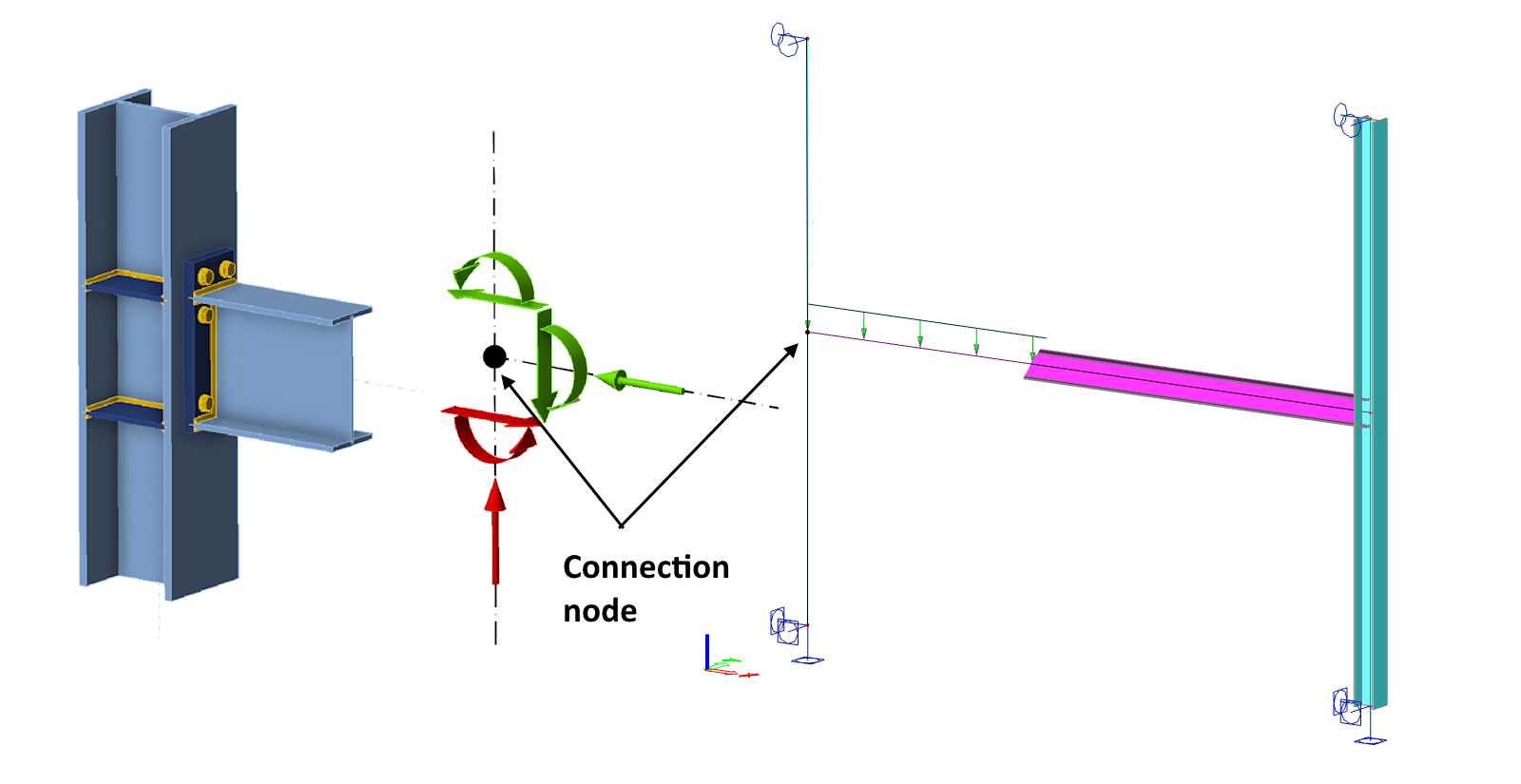
Principy zatěžování styčníku v Connection, MKP model v pozadí
1 Výpočtový model
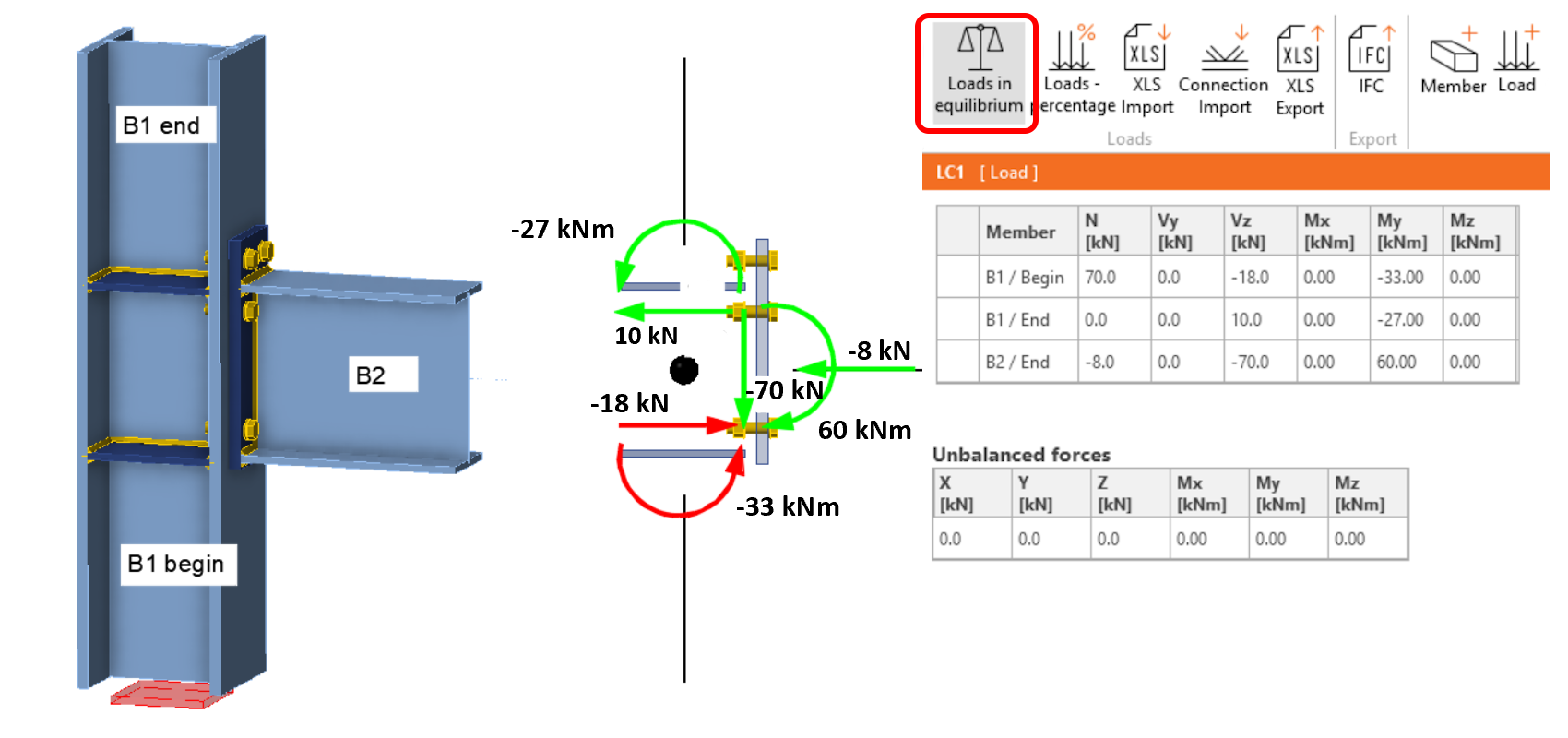
Výpočtový model v Connection, stejně jako každý jiný FEM model, má okrajové podmínky a je nějakým způsobem zatěžován. Strukturu výpočtového modelu si popíšeme na konkrétním příkladu přípoje. Mějme následující jednoduchý rovinný rám s přípojem průvlaku IPE240 na sloup z profilu HEB200. Průvlak je zatížen spojitým rovnoměrným zatížením a momentový přípoj průvlaku na sloup je tuhý, pomocí čelní desky. Vizualizace styčníku je na následujícím obrázku.
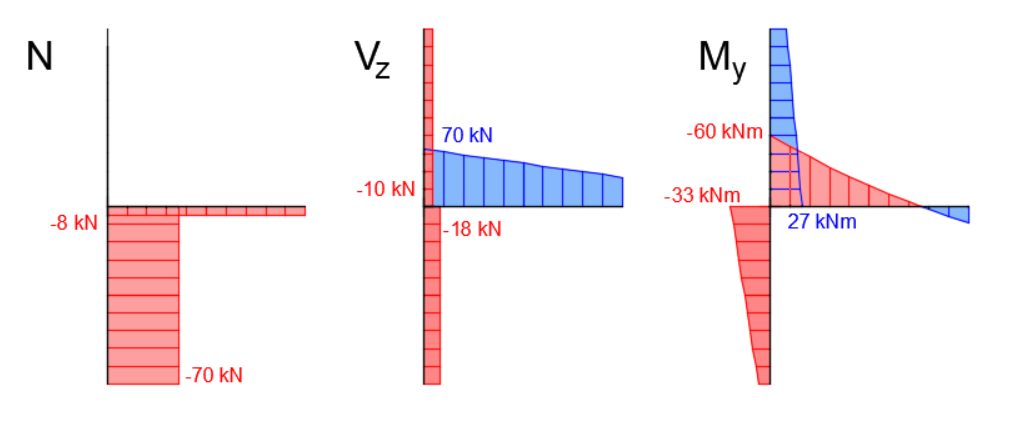
3D výpočtový model styčníku se v aplikaci Connection zatěžuje vnitřními silami působícími v jednotlivých prutech bezprostředně u uzlu přípoje (pozn. při objemovém zobrazení se zatížení modelu silami a momenty vykresluje na koncích vizualizovaných zárodků připojených prvků, což může být při prvním použití aplikace zavádějící). Střed styčníku, reprezentovaný v osovém zobrazení přípoje v aplikaci černým bodem, je tak shodný s uzlem globálního MKP prutového modelu. Vnitřní síly výseku konstrukce v okolí styčníku, stanovené pomocí globálního prutového MKP modelu, jsou na následujícím obrázku. Hodnoty vnitřních sil v uzlu jsou na obrázku uvedeny číselně.
Pro posouzení přípoje lze v aplikaci zvolit dva odlišné přístupy k modelování přípoje:
- Zatížení styčníku je v rovnováze
- Zatížení styčníku není v rovnováze
Varianty se liší okrajovými podmínkami a způsobem zatěžování výpočtového modelu. Způsob analýzy styčníku se přepínají pomocí tlačítka Zatížení v rovnováze v části Load v horním pásu karet.
Nejprve v článku podrobně rozebereme podepření a zatížení výpočtového modelu, odpovídající volbě Zatížení v rovnováze. Pomocí této varianty modelu lze posuzovat celý uzel přípoje jako jeden celek, zatěžujeme všechny připojené prvky. Jedná se o výchozí nastavení programu po založení nového projektu.
Variantu podepření modelu a způsob jeho zatížení s vypnutou funkcí Zatížení v rovnováze si podrobně rozebereme později v kapitole 3. Tato varianta je vhodná např. pro izolované posouzení přípojů jednotlivých samostatných prvků.
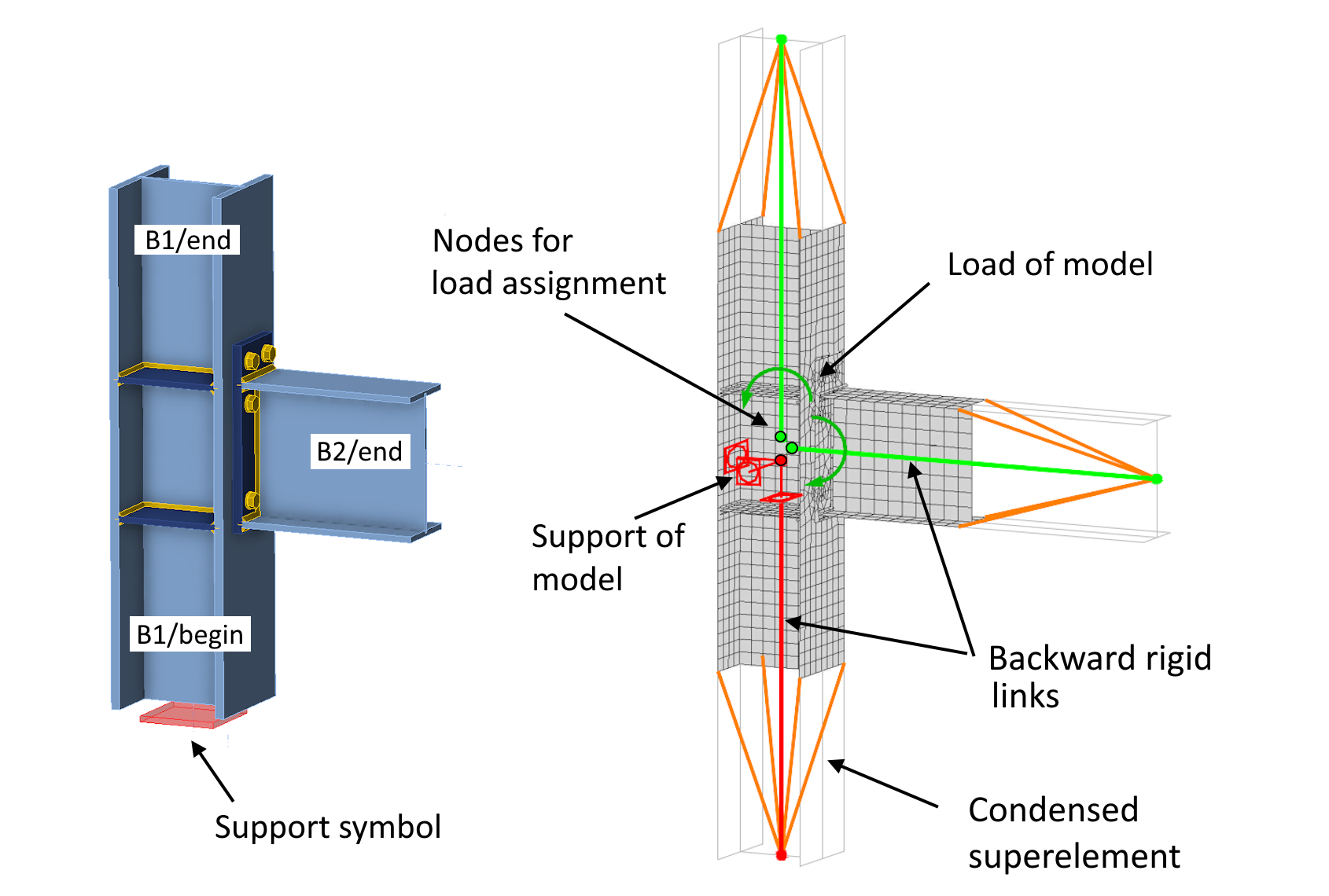
V aplikaci Connection je model našeho přípoje tvořen jedním průběžným prvkem (sloup B1) a jedním ukončeným prvkem (průvlak B2). Jako nosný prvek je nastaven sloup. Výpočtový model (varianta zatížení v rovnováze!) je schématicky zobrazen na následujícím obrázku.
MKP výpočtový model přípoje se skládá z:
- Připojené prvky – je modelován vždy zárodek připojeného prvku (nosník, sloup, diagonála atd.) přiléhající ke styčníku. Průřez prvku je modelován pomocí deskostěnových plastických prvků.
- Části přípoje – čelní desky, styčníkové plechy, výztuhy, žebra atd. Opět modelováno pomocí deskostěnových plastických prvků.
- CBFEM komponenty – svary, šrouby, kontakty, MPC vazby atd. Tyto části modelu nejsou hlavním předmětem tohoto článku a jsou popsány v teoretických základech.
- Kondenzované superelementy – zajišťují hladký roznos bodového zatížení do prostorového deskostěnového modelu připojeného prvku. Tyto prvky nejsou uživateli ve scéně viditelné. Detailněji jsou popsány v tomto článku.
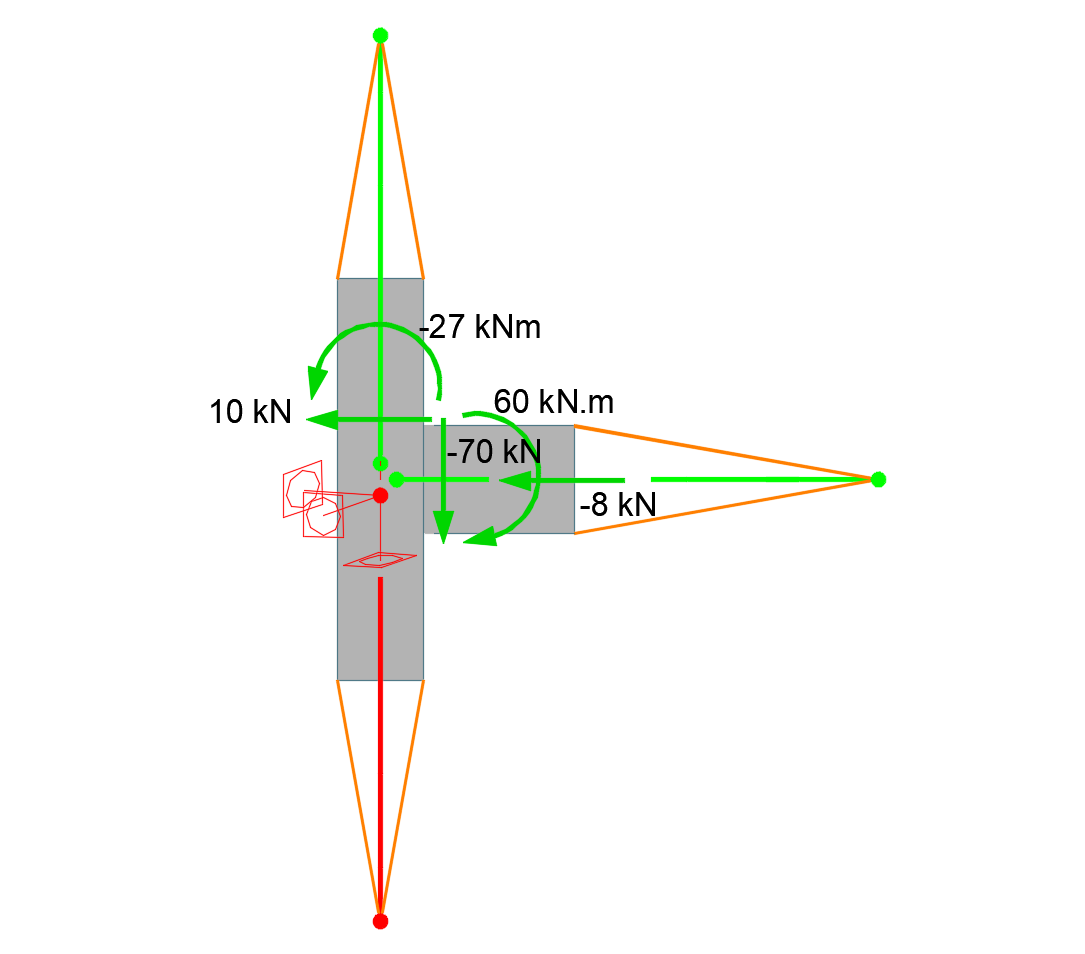
- Zpětná tuhá ramena – Každý konec připojeného prvku (přesněji řečeno konec kondenzovaného superelementu, který prvek prodlužuje), je propojen s pomocným uzlem ve středu styčníku pomocí „zpětného“ tuhého ramene. Každé tuhé rameno má ve středu styčníku vlastní uzel. Na tyto uzly se aplikují okrajové podmínky výpočtového modelu a zadává se do nich zatížení přípoje ve formě bodových sil a momentů.
- Podpory – okrajové podmínky CBFEM modelu aplikovány na počáteční uzel jednoho zpětného tuhého ramena.
1.1 Podpory
Každý MKP výpočtový model potřebuje podpory, aby nebyl singulární. CBFEM model je v principu obecný 3D MKP model a to znamená, že potřebuje tři podpory proti posunu a tři proti rotaci. Jak je zakresleno na obrázku modelu, v našem příkladě je bodová podpora (tři posuny a tři rotace) zadána do uzlu zpětného tuhého ramene, které spojuje spodní konec sloupu s pomocným uzlem ve středu styčníku. Přičemž podpora je zadána do uzlu ve středu styčníku.
Rozhodnutí, na který z prvků (přesněji jeho zpětné tuhé rameno) bude podpora aplikována, se řídí tím, který připojený prvek je v aplikaci nastaven jako tzv. nosný. V aplikaci je pak podepřený konec nosného prvku vizualizován pomocí symbolu červeného čtverce.
1.2 Zatížení
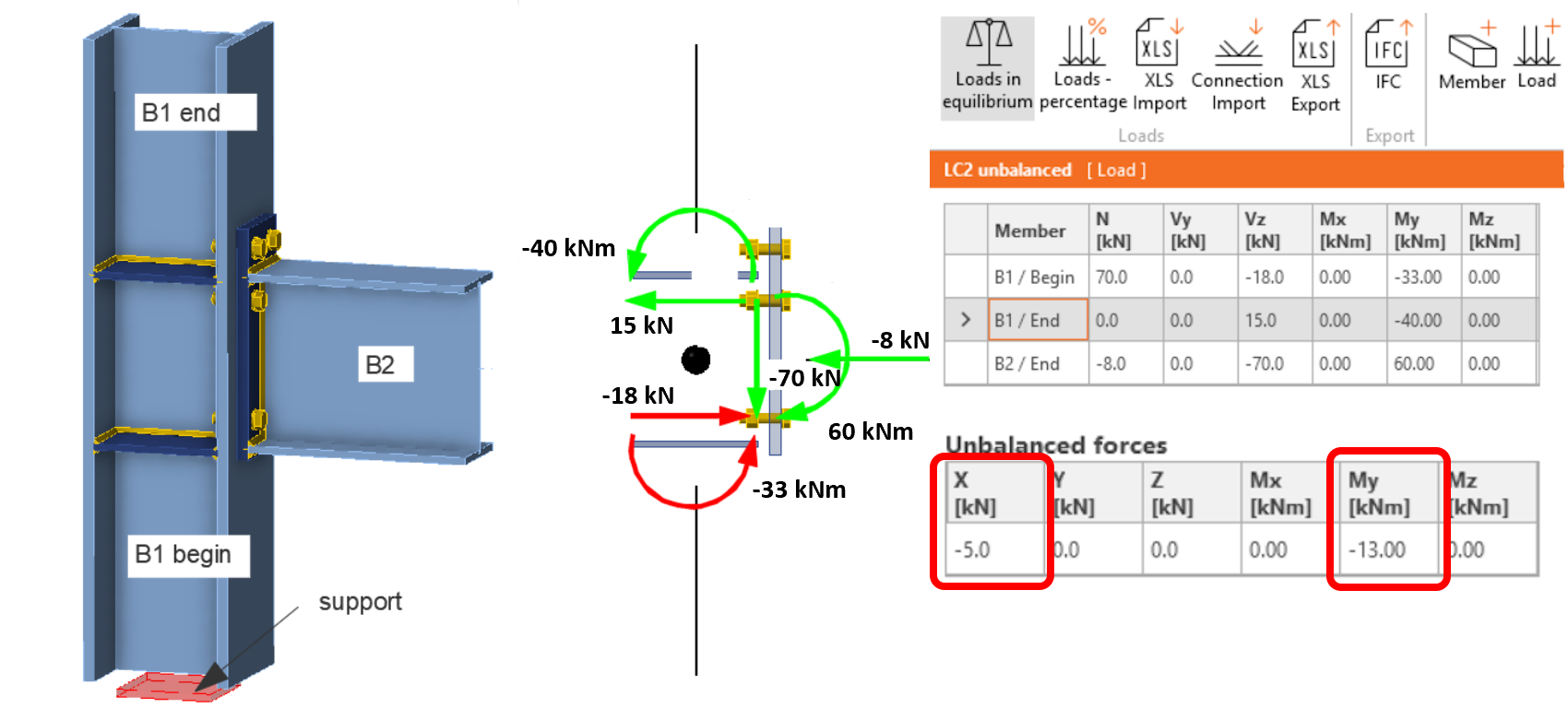
Při použití funkce Zatížení v rovnováze se vnitřní síly zadávají na všechny prvky přípoje. Správně zadané zatížení přípoje pak musí splňovat základní statický princip: síly ve styčníku musí být v rovnováze. Dodržení tohoto pravidla je velmi důležité pro správné posouzení přípoje. Splnění rovnováhy program kontroluje a pod tabulkou, kde se zadává zatížení, rovněž vypisuje tabulku vypočtených tzv. Nevyvážených sil. Pokud je přípoj zadán správně, jsou nevyvážené síly nulové (nebo téměř nulové). Zatížení řešeného styčníku je zobrazeno na následujícím obrázku, nevyvážené síly jsou nulové, zatížení je tedy zadáno správně. Efekt nesprávně zadaného zatížení, kdy v modelu vzniknou Nevyvážené síly a proč mohou způsobit zcela nekorektní posouzení styčníku, rozebereme později na dvou příkladech.
Zatížení modelu se aplikuje (stejně jako podpory modelu) na začátky zpětných tuhých ramen spojujících střed styčníku a konec kondenzovaného superelementu. Jinými slovy do výpočtového modelu se zadávají přímo uzlové vnitřní síly ve středu styčníku, které byly vyplněny v tabulce zatížení. Zpětná tuhá ramena následně zajišťují, že ohybový moment ze středu styčníku je transformován na ohybový moment v místě konce kondenzovaného superelementu.
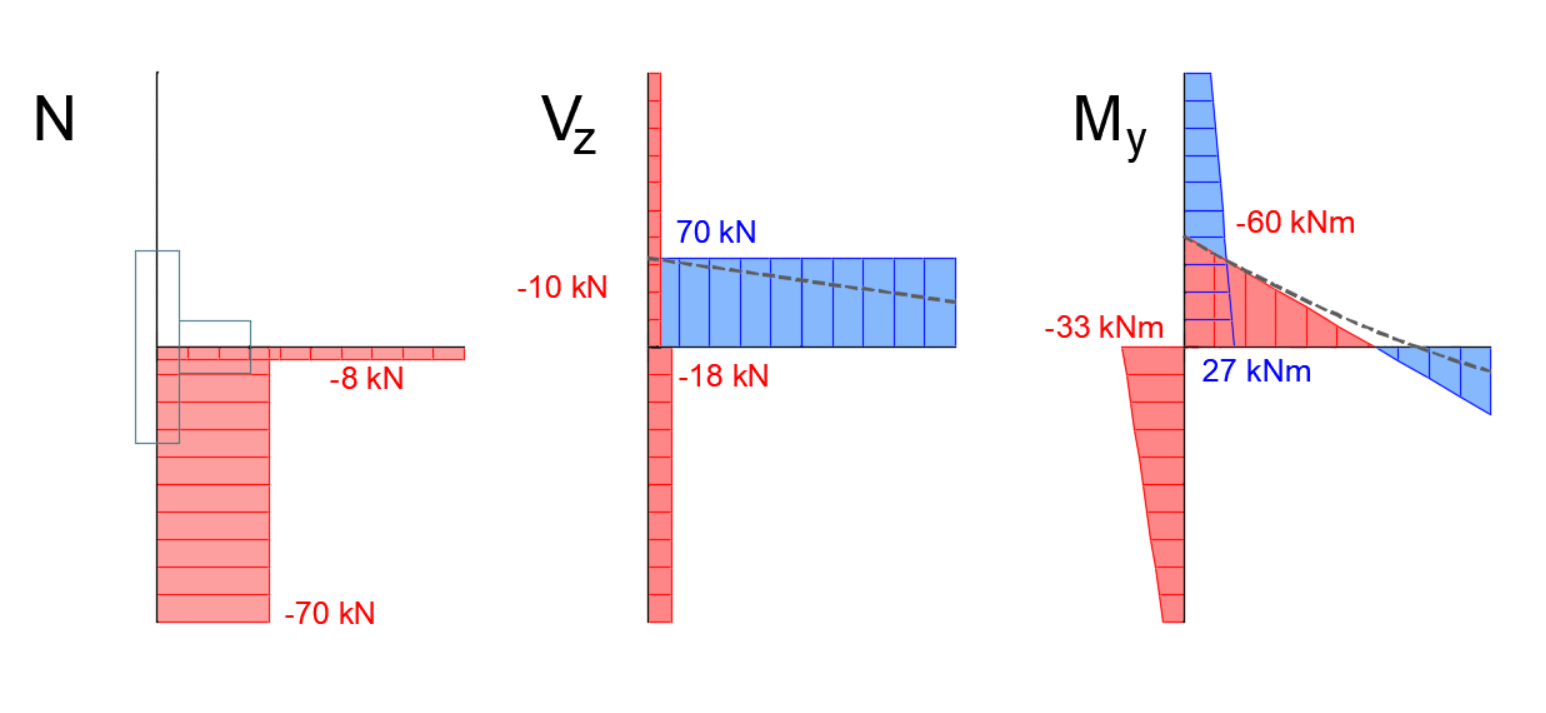
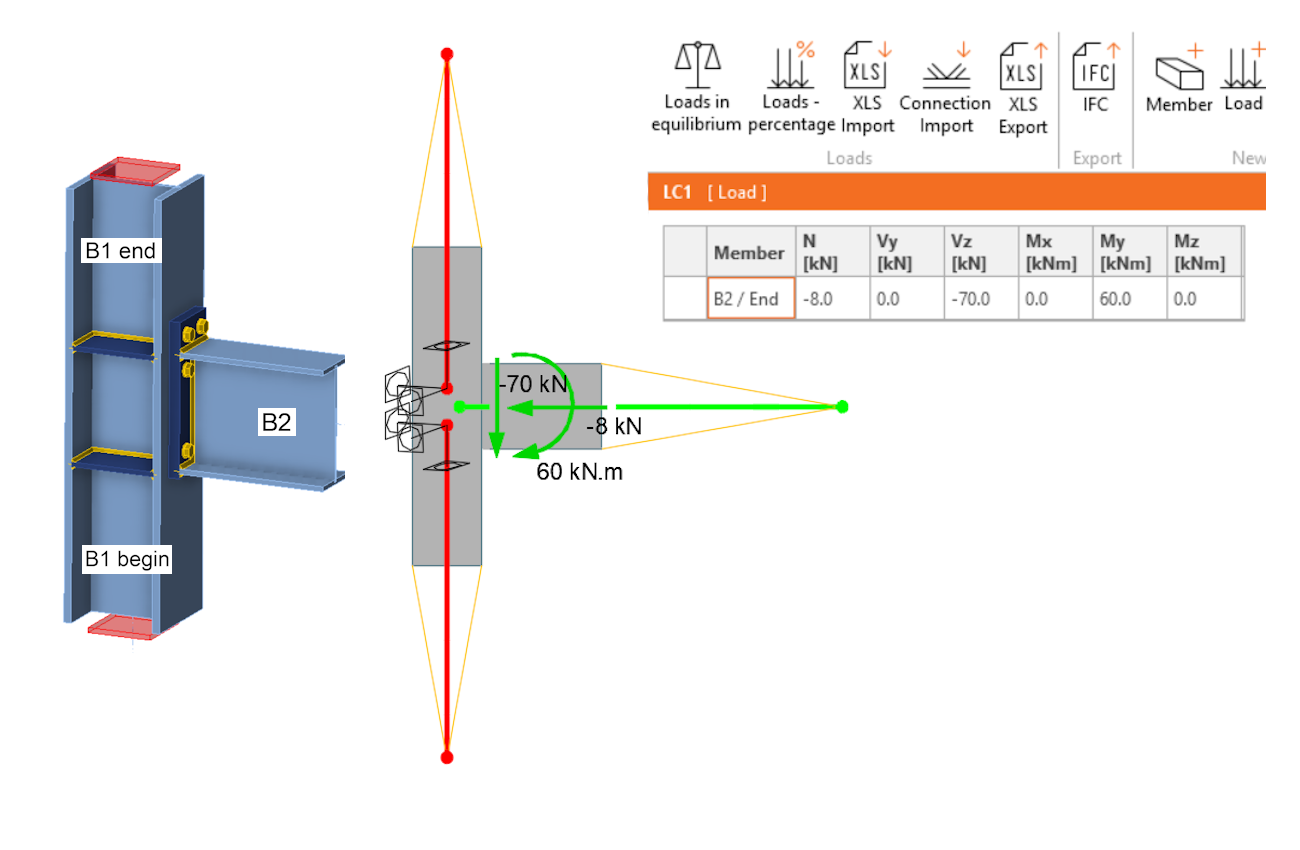
Ukažme si funkci zpětného tuhého ramene názorněji na jednoduchém prutovém modelu, kde bude vodorovný prvek B2 místo deskostěnového 3D modelu reprezentován náhradním prutem. Vnitřní síly na prvku ve středu styčníku jsou převzaty z příkladu. Tedy Vz = -70 kN, My = 60 kN.m. Tyto síly jsou zadány na začátek tuhého ramene. Odtud jsou přeneseny na konec kondenzovaného superelementu a odtud do vlastního modelu připojeného prvku B2. Jak je vidět, vnitřní síly na prvku B2 na jeho začátku (střed styčníku) jsou shodné se zadáním.
Zpět k řešenému styčníku. Je zřejmé, že výsledný 3D výpočtový model je podepřen staticky určitě (odebráno je právě jen šest stupňů volnosti) a může se volně deformovat bez vzniku staticky neurčitých reakcí, která by změnily zadaný tok sil. Také je zřejmé, že zadávat zatížení na začátek zpětného tuhého ramene B1/begin, kde jsou zadány podpory modelu, by bylo zbytečné, protože síly a momenty by byly přímo zachyceny podporami. Výpočtový model je tedy zatížen silami v B1/end a B2/end, to znamená jen ve dvou ze tří prvků, třetí je podepřen. Pokud je ale zatížení styčníku korektní, zadané síly jsou v rovnováze, reakce vypočtené v podporách B1/begin budou totožné se zatížením definovaným v tabulce. Zatížení modelu styčníku je pak následující:
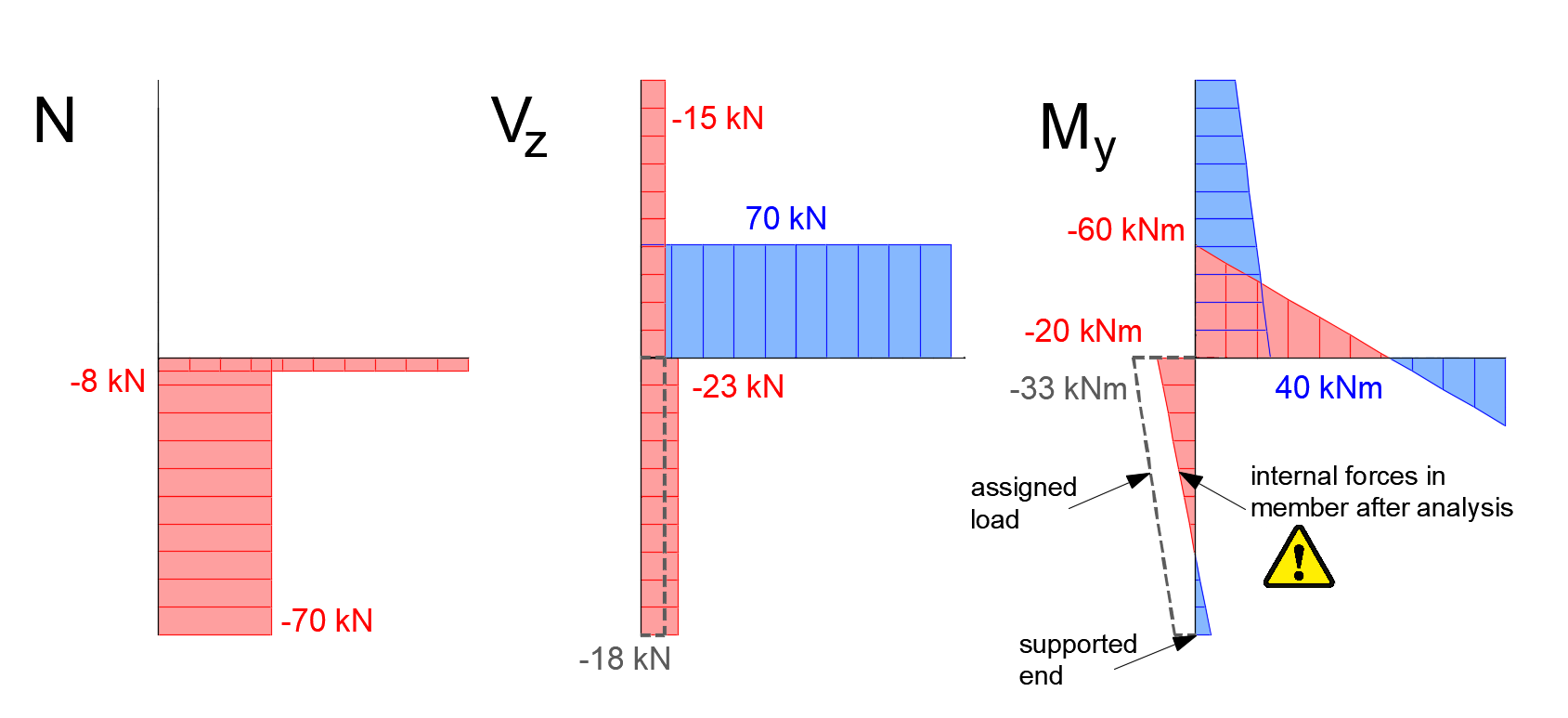
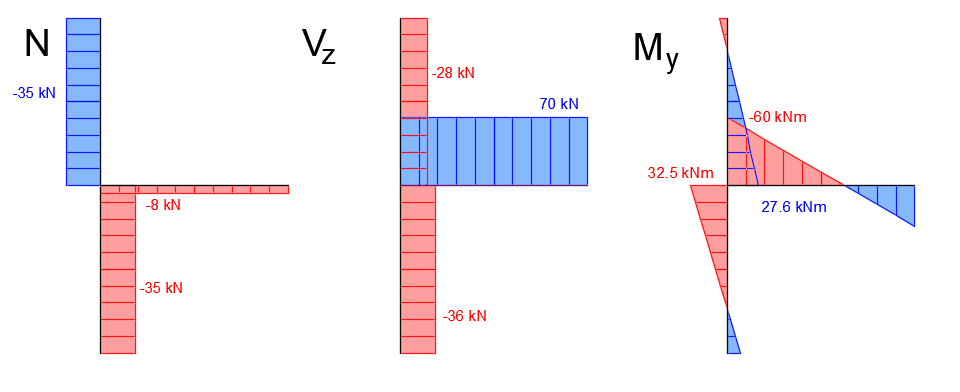
Průběh vnitřních sil na stejně zatíženém a podepřeném náhradním prutovém modelu je uveden na následujícím obrázku. Vizualizovány jsou jen síly na řešených prvcích, zpětná tuhá ramena jsou vynechána. Čárkovaně jsou zakresleny také průběhy vnitřních sil z globálního MKP modelu, které byly uvedeny na začátku článku. Jak je vidět, vzhledem k absenci liniového zatížení průvlaku v Connection je např. průběh momentů lineární oproti původnímu parabolickému. V místě přípoje však dostatečně odpovídá průběhu z globálního MKP modelu. Obdobně posouvající síla na modelu v Connection je konstantní oproti lineárnímu průběhu z globálního modelu.
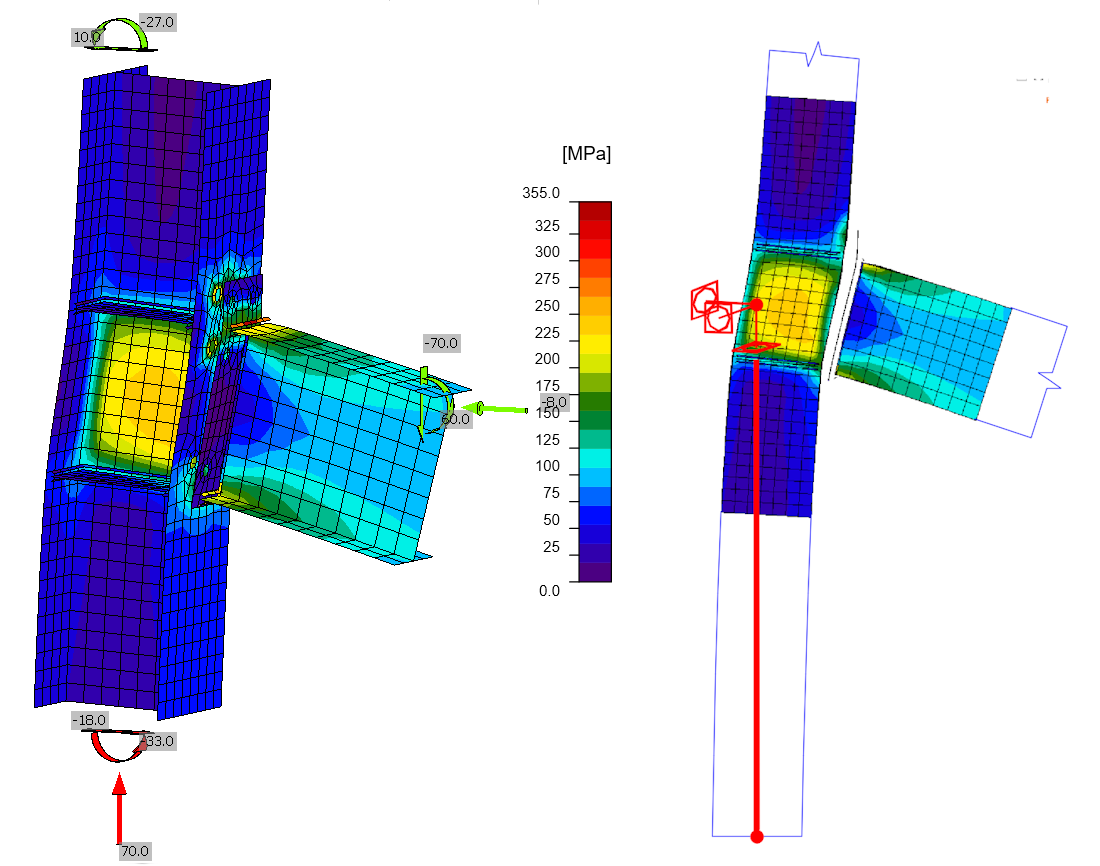
Pro ilustraci je na obrázku níže uveden deformovaný model po výpočtu spolu s obrysem nedeformovaného modelu. Z průběhu deformace je zřejmé, že podpora modelu je na spodním konci sloupu. Prostřednictvím tuhého ramene, ve skutečnosti je podpora v modelu ve středu styčníku samozřejmě.
2 Pozor na nevyvážené síly ve styčníku
Ukázali jsme si, jak v principu vypadá MKP výpočtový model styčníku, jak je podepřen a jak je zatížen. Ve výše uvedeném příkladu platilo, že zadané zatížení bylo v rovnováze. Nyní si ukážeme, jaký efekt na zatížení modelu a napjatost přípoje má, pokud zadané zatížení není v rovnováze.
2.1 Nevyvážené síly v rámovém styčníku
Použijeme stejný příklad tuhého rámového přípoje pomocí čelní desky. Zadané, záměrně nekorektní, zatížení přípoje je uvedeno na obrázku níže. V tabulce Nevyvážené vnitřní síly program vypsal následující síly Fx= -5 kN a My = 13kN.m.
Průběh vnitřních sil takto zatíženého modelu po výpočtu si opět ukážeme na zjednodušené prutové reprezentaci modelu přípoje.
Na spodní části sloupu B1/begin (podepřený konec nosného prvku) je pro porovnání rovněž čárkovaně uveden průběh ohybových momentů a posouvajících sil odvozený ze sil zadaných do B1/begin v tabulce v aplikaci. Je vidět, že hodnoty skutečně působících momentů na sloupu se zásadně liší od toho, co uživatel zadal na B1/begin. A liší se právě o hodnoty nevyvážených sil momentu My a Vz. Proč tomu tak je? Jak jsme si již vysvětlili, vnitřní síly zadané na podepřený konec nosného prvku (B1/begin) se do modelu ve skutečnosti neaplikují, ale jsou výsledkem řešení MKP modelu jako reakce v podporách nosného prvku, resp. v podporách výpočtového modelu. Efekt nevyvážek v tomto příkladě je tedy takový, že podepřený nosný prvek je posouzen na zcela jiné (nižší!) vnitřní síly, než uživatel zadal do tabulky zatížení. Z tohoto důvodu je nutné se vždy snažit mít nulové nebo minimální nevyvážení síly ve styčníku.
Pro úplnost dodejme, že konkrétně v tomto případě je vlastní přípoj průvlaku (šrouby, čelní deska, svary) posouzen v podstatě korektně, protože na nepodepřený prvek B2 je v modelu aplikováno přesně to zatížení, které bylo zadáno v tabulce.
2.2 Nevyvážené síly ve styčníku příhradoviny
Na tomto příkladu si ukážeme, kdy efekt nesprávně zadaného zatížení s nevyváženými silami ve styčníku vede na zcela chybné posouzení přípoje prvku. Použijeme následující uzel příhradové konstrukce, který je tvořen spodním taženým pásem, jednou taženou a jednou tlačenou diagonálou. Spodní tažený pás je přerušen montážním šroubovaným stykem. Pro názornost budeme pracovat jen s normálovými silami ve styčníku.
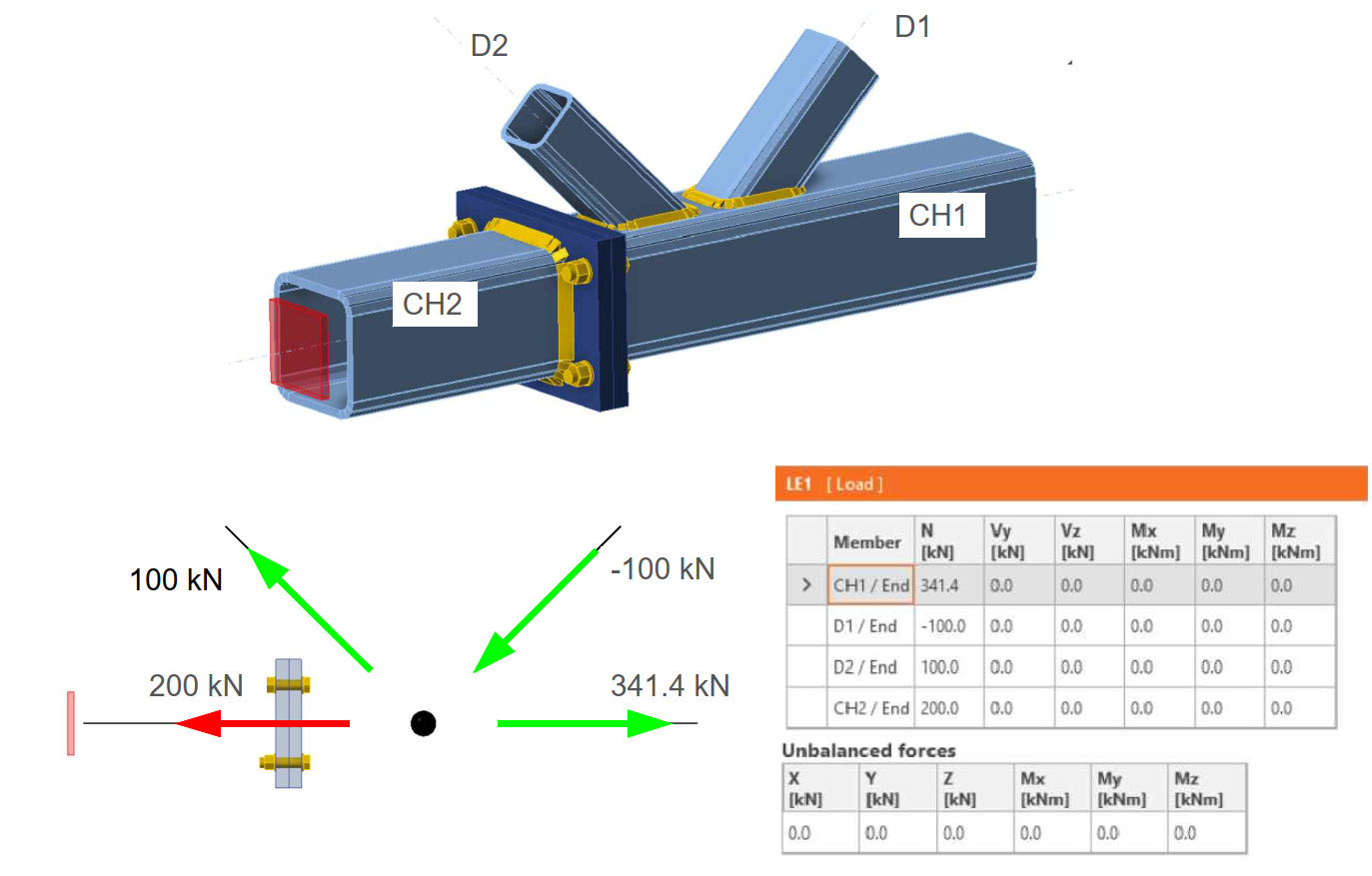
Na obrázku výše je uvedeno korektní zadání vnitřních sil, které jsou v rovnováze. Výsledné normálové síly po výpočtu modelu v prvcích příhradoviny (opět zjednodušeně na prutové reprezentaci modelu) a tahové síly ve šroubech montážního styku budou následující. Tahová síla ve šroubu, včetně páčení, je 73 kN.
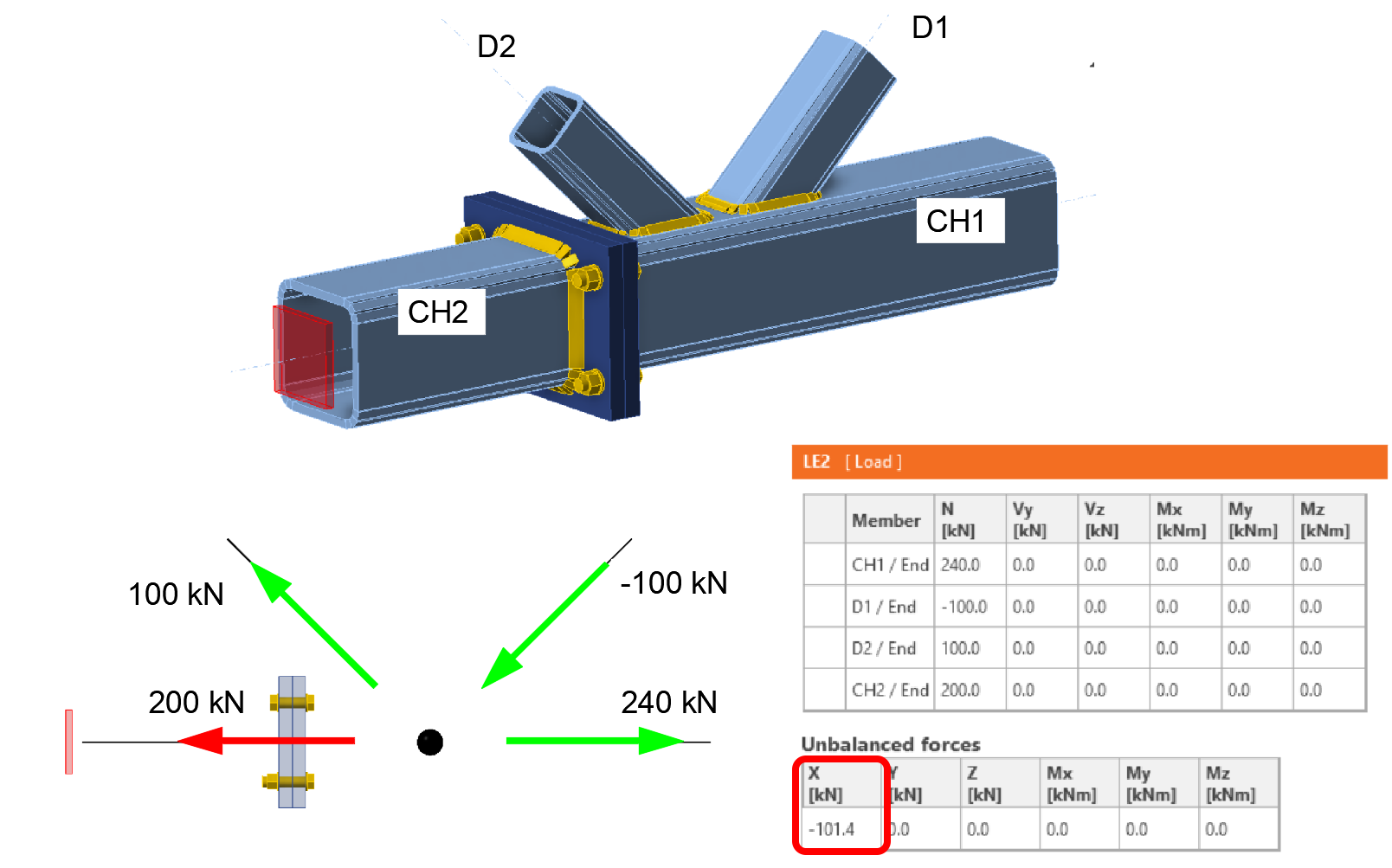
Nyní provedeme rozbor stejného styčníku se zatížením, které není v rovnováze ve vodorovném směru X. Zatížení styčníku je totožné s předchozím příkladem, pouze na spodní tažený pás CH1 je chybně zadána normálová síla 240 kN, která způsobuje nevyváženou sílu ve směru X rovnou 101.4 kN.
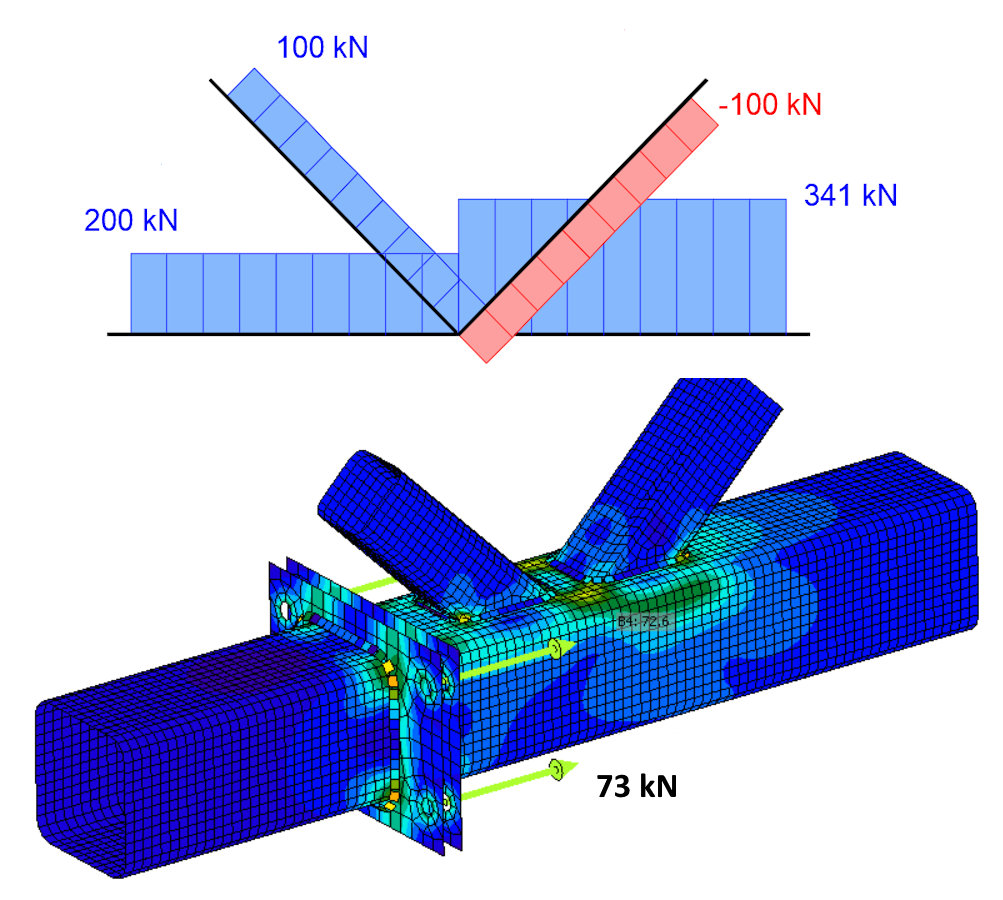
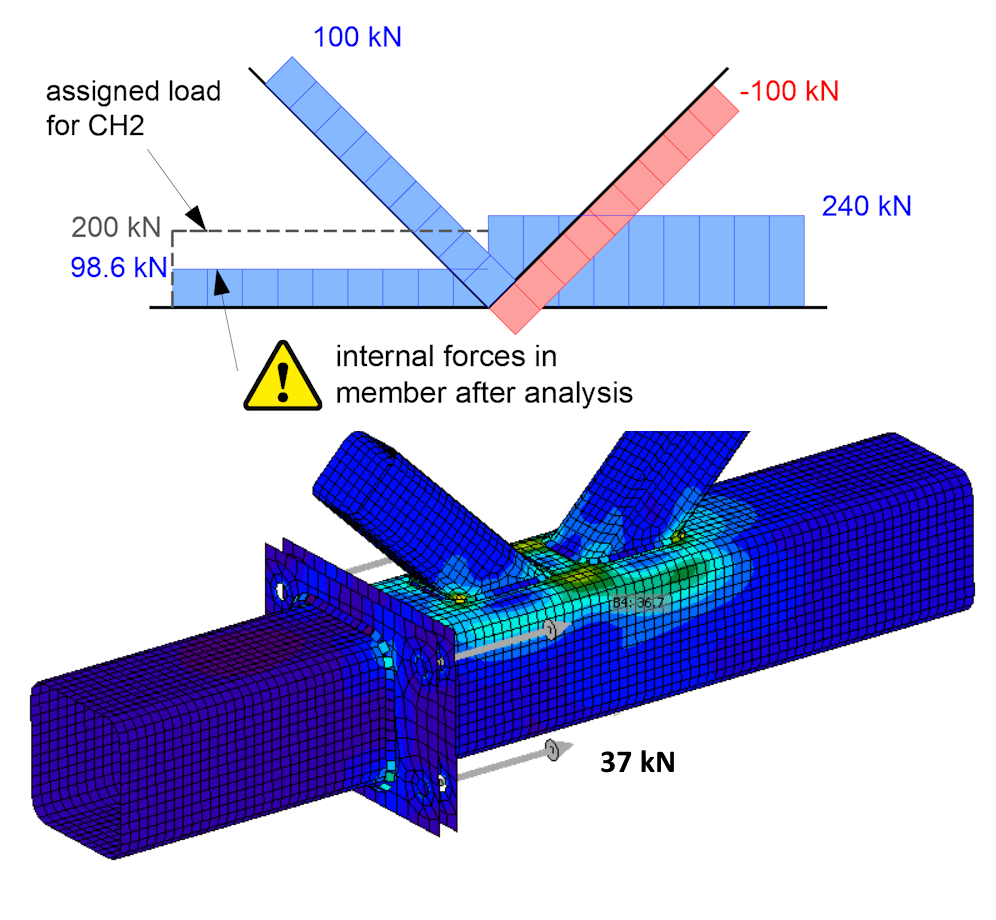
Výsledné normálové síly v prvcích příhradoviny po výpočtu modelu a tahové síly ve šroubech montážního styku budou následující.
Efekt nevyvážených sil v přípoji v tomto příkladě je tedy takový, že podepřený nosný prvek CH2 je posouzen na zcela jiné (nižší!) vnitřní síly, než uživatel zadal do tabulky zatížení. A co je ještě důležitější, rovněž šroubový přípoj je posouzen na podstatně nižší tahovou sílu 98.6 kN, než byla prvku zadána v tabulce zatížení. Tahová síla ve šroubu, včetně páčení, je 37 kN.
3 Výpočtový model s vypnutou funkcí Zatížení v rovnováze
Doteď jsme pracovali v aplikaci Connection se zapnutou funkcí zatížení v rovnováze. Nyní si rozebereme zatížení a podepření výpočtového modelu, pokud je funkce Zatížení v rovnováze vypnuta.
Opět použijeme dříve řešený přípoj vodorovného průvlaku na sloup pomocí šroubované čelní desky. Vypnutí funkce Zatížení v rovnováze znamená, že průběžný prvek (sloup B1) je podepřen na obou koncích a rovnováha zatížení na příčníku není kontrolována. Na podepřené konce průběžného prvku (sloup B1) není možné zadat v tabulce zatížení. Jediný zatížený prvek je zde průvlak B2. Výpočtový model a zatížení přípoje pak vypadá takto.
Průběh vnitřních sil takto zatíženého a podepřeného modelu po výpočtu si opět ukážeme na zjednodušené prutové reprezentaci modelu přípoje. Posouvající síla Vz na průvlaku se ve sloupu rozdělila na tahovou sílu v horní části sloupu a tlakovou ve spodní části sloupu. Je např. zřejmé, že dosáhnout logického průběhu normálových sil na sloupu, kdy posouvající síla z průvlaku bude ve formě tlakové síly směřovat do základu rámu pomocí tohoto modelu nelze. Obdobně rozdělení ohybových momentů na sloupu odpovídá podepření výpočtového modelu a nemusí odpovídat skutečnému toku vnitřních sil v konstrukci.
Důležité ale je, že průběhy vnitřních sil na zatíženém prvku B2 nejsou staticky neurčitým podepřením modelu ovlivněny a platí, že posouzení vlastního prvku B2 a jeho přípoje (čelní desky, šroubů svarů) je korektní. Ale stav napjatosti sloupu již neodpovídá skutečnému působení v konstrukci, koneckonců ani na něj nebylo zadáno žádné zatížení. Z toho je zřejmé, že s vypnutím funkce zatížení v rovnováze lze posuzovat odděleně přípoje jednotlivých prvků, zatímco se zapnutou funkcí zatížení v rovnováze lze posoudit celý uzel přípoje, a to s uvážením interakce globálních účinků (např. napjatost ve sloupu od působící N+M v konstrukci) a lokálních účinků (např. příčný ohyb pásnice HEA nosníku od momentově namáhaného šroubového přípoje).