Štíhlý železobetonový sloup prefabrikované haly (EN)

1 Zadání

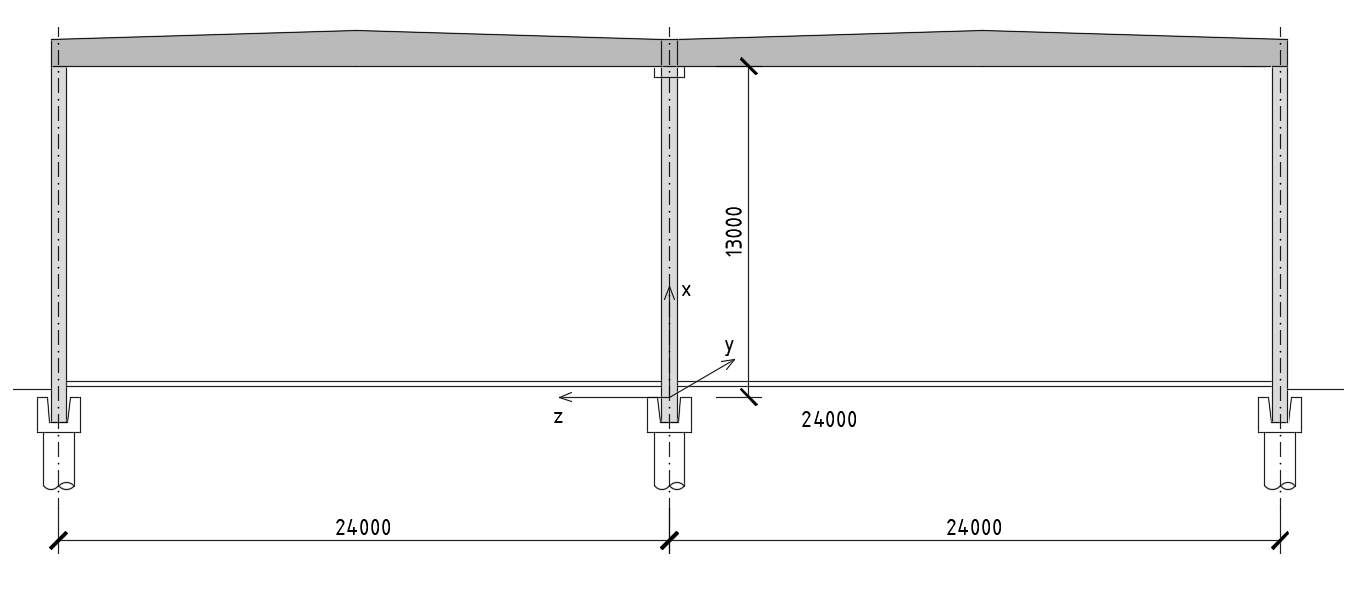
Schéma posuzované konstrukce je na obrázku níže. Jedná se o dvoulodní prefabrikovanou halu s osovou vzdáleností sloupů 24.0 m. Posuzován bude vnitřní sloup délky 13.0 m. Sloup je dole vetknutý do kalichu, uloženého na hlavě velkoprůměrové piloty. Hala je bez ztužení, staticky tak jednotlivé sloupy působí jako dole vetknuté konzoly, není uvažováno vzájemné spolupůsobení jednotlivých sloupů v mezním stavu únosnosti.

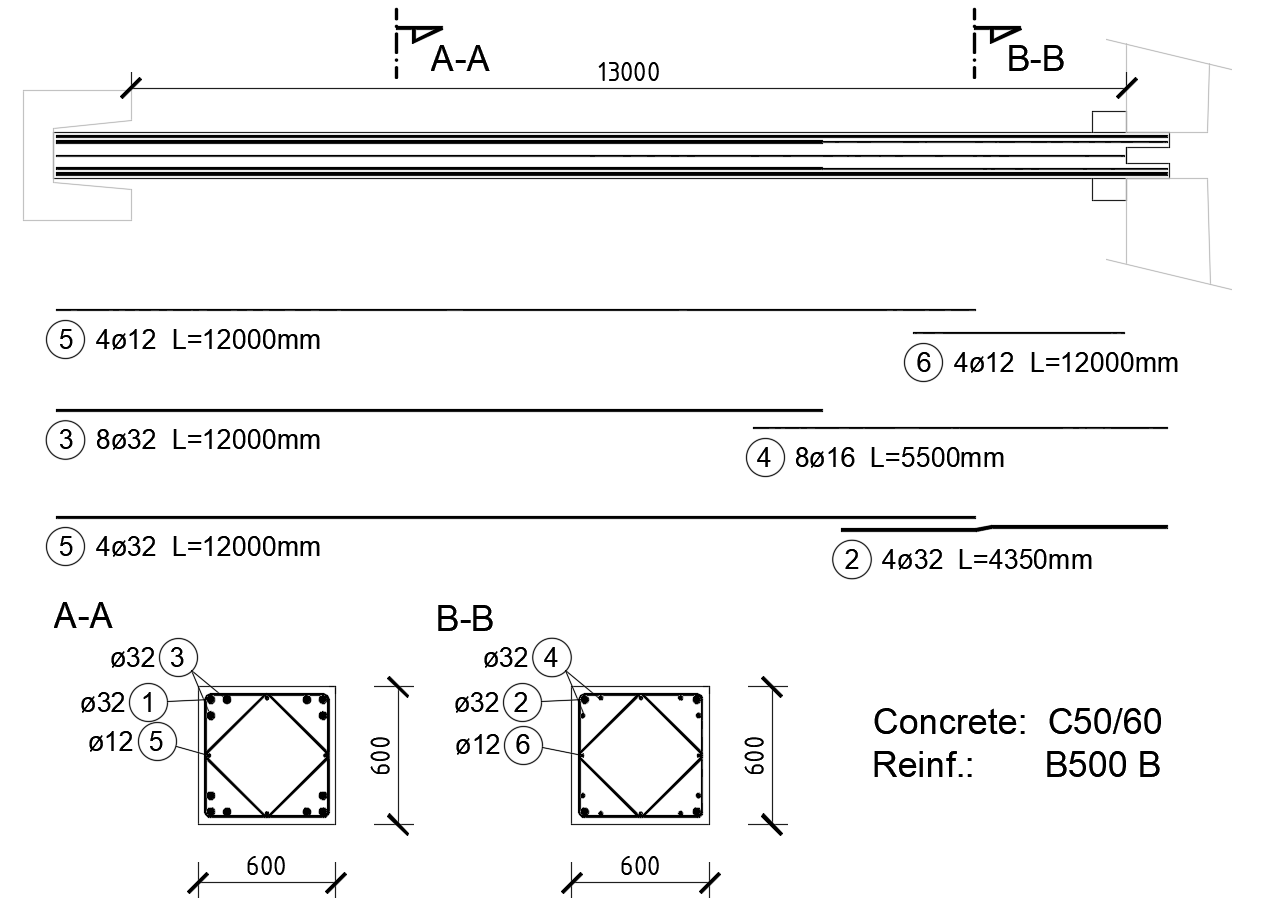
Vyztužení prefabrikovaného sloupu je následující.

Modul pružnosti betonu E_cm je zjištěn zkouškami a má velikost 34 GPa. Součinitel dotvarování pro čas mezi aplikací stálého zatížení a návrhovou životností je φ(t_∞,t₀) = 1.5.

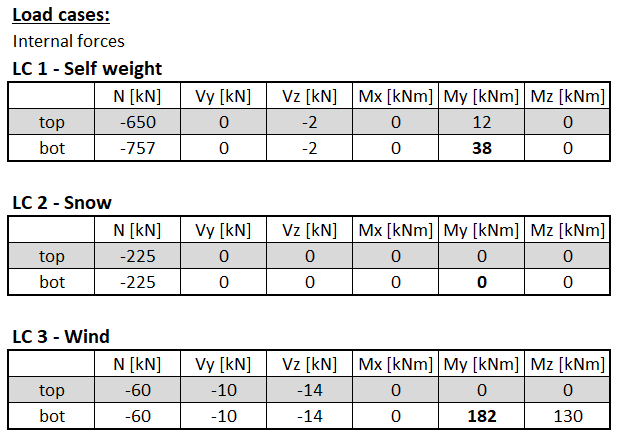
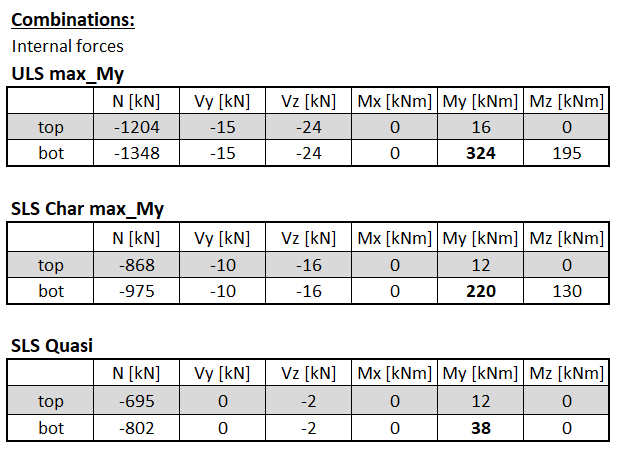
Střední sloup je od vlastní tíhy zatížen téměř centricky, relativně malý příčný ohybový moment je způsoben uvážením rozdílné vlastní tíhy konstrukce levé a pravé lodi haly. Rozhodující pro posouzení konzoly sloupu je pak ohyb od zatížení větrem. Vnitřní síly ve vrcholu a patě sloupu jsou uvedeny v následujících tabulkách.

Geometrická imperfekce je uvažována dle článku 5.2, ČSN EN 1992-1-1.  Její hodnota byla stanovena na 43 mm. Pro posouzení v tomto návodu je uvažována ve směru většího ohybového momentu, to znamená ve směru Z lokálního souřadného systému sloupu.

2 Metoda posouzení

2.1 Princip

Materiálově a geometricky nelineární metoda výpočtu v IDEA StatiCa Member je založená na použití speciálního prutového konečného prvku, kde je průřez rozdělen na jednotlivá „vlákna“ (beton a výztuž), přičemž vlákna reprezentující tažený beton se během nelineárního výpočtu „vypínají“ a zohledňuje se tak pokles tuhosti potrhaného železobetonového průřezu. Metoda odpovídá obecné nelineární metodě pro posouzení štíhlých tlačených prvků dle ČSN EN 1992-1-1, kapitola 5.8.6.

Postup posouzení v programu Member se děje ve třech krocích:

1. MNA - Materiálově nelineární výpočet (s vlivem potrhání betonu, plastického působení betonu v tlaku a pružnoplastického působení výztuže).
2. LBA - Výpočet tvarů vybočení pomocí linear buckling analysis. Geometrická imperfekce se zadává ve tvaru vypočteného tvaru vybočení. Přičemž hodnota imperfekce se zvětšuje o vliv dotvarování, viz. dále.
3. GMNIA – Finální posouzení, gemetricky a materiálově nelineární výpočet s imperfekcí.

Podrobněji o metodě výpočtu v aplikaci Member pojednává například článek Materiálově a geometricky nelineární analýza štíhlých mostních prvků v IDEA StatiCa Member.

2.2 Vliv dotvarování

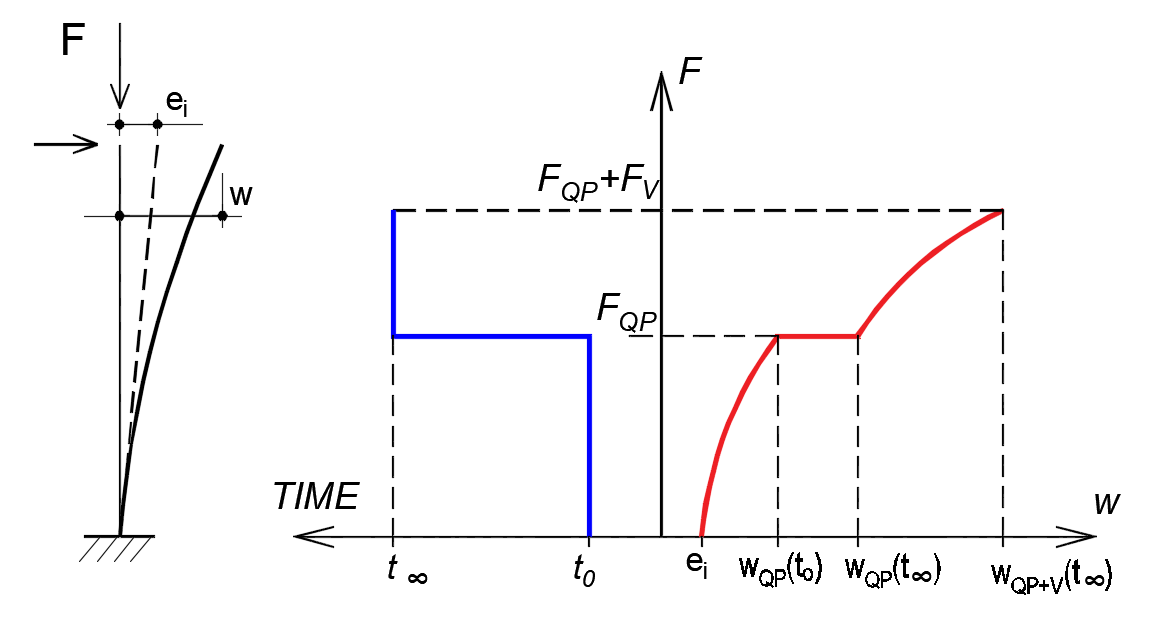
Program Member aktuálně neumí automaticky zohlednit vliv dotvarování betonu na únosnost tlačeného prvku. Podstata chování štíhlého tlačeného prvku v čase je schématicky zobrazena na následujícím obrázku, kde je znázorněn nárůst deformace od dlouhodobých složek zatížení (QP) a celková deformace při aplikaci proměnného  zatížení (V) v čase na konci životnosti. Z obrázku je zřejmé, že nárůst příčné deformace tlačeného prvku vlivem dotvarování zvyšuje účinky II. řádu při posouzení prvku.

Tento vliv je nutno zadat do výpočtu ručně pomocí zjednodušené metody, kdy se vliv dotvarování zadává pomocí navýšení počáteční geometrické imperfekce. Podrobněji o problematice pojednává článek Jak zohlednit dotvarování u štíhlého betonového sloupu v aplikaci Member. V odkazovaném článku je uvedena iterační metoda pro výpočet vlivu dotvarování. V tomto návodu bude použita jednodužší metoda, kdy nárůst příčné deformace v čase je vypočten jako rozdíl deformace od kvazistálé kombinace v časech t₀ a t_∞

w_QP (t₀)  -  průhyby (vodorovné deformace) od dlouhodobých zatížení v čase t₀. Stanoví se pomocí GMNIA výpočtu kvazistálé kombinace s E_cm

w_QP (t_∞)  -  průhyby (vodorovné deformace) od dlouhodobých zatížení v čase t_∞. Stanoví se pomocí GMNIA výpočtu kvazistálé kombinace s efektivním modulem pružnosti E_c,eff

E_c,eff = E_cm/[1+φ(t_∞,t₀)]

kde φ(t_∞,t₀) je součinitel dotvarování mezi časy aplikace dlouhodobých stálých zatížení a návrhovou životností konstrukce

Rozdíl krátkodobé a dlouhodobé deformace je pak 

Δ e_i = w_QP (t_∞) - w_QP (t₀) 

O tuto hodnotu se pak pro finální GMNIA výpočet navýší počáteční imperfekce e_i definovaná normou.

3 Posouzení sloupu

3.1 Nový projekt

Otevřete program IDEA StatiCa a spusťte aplikaci Member. 

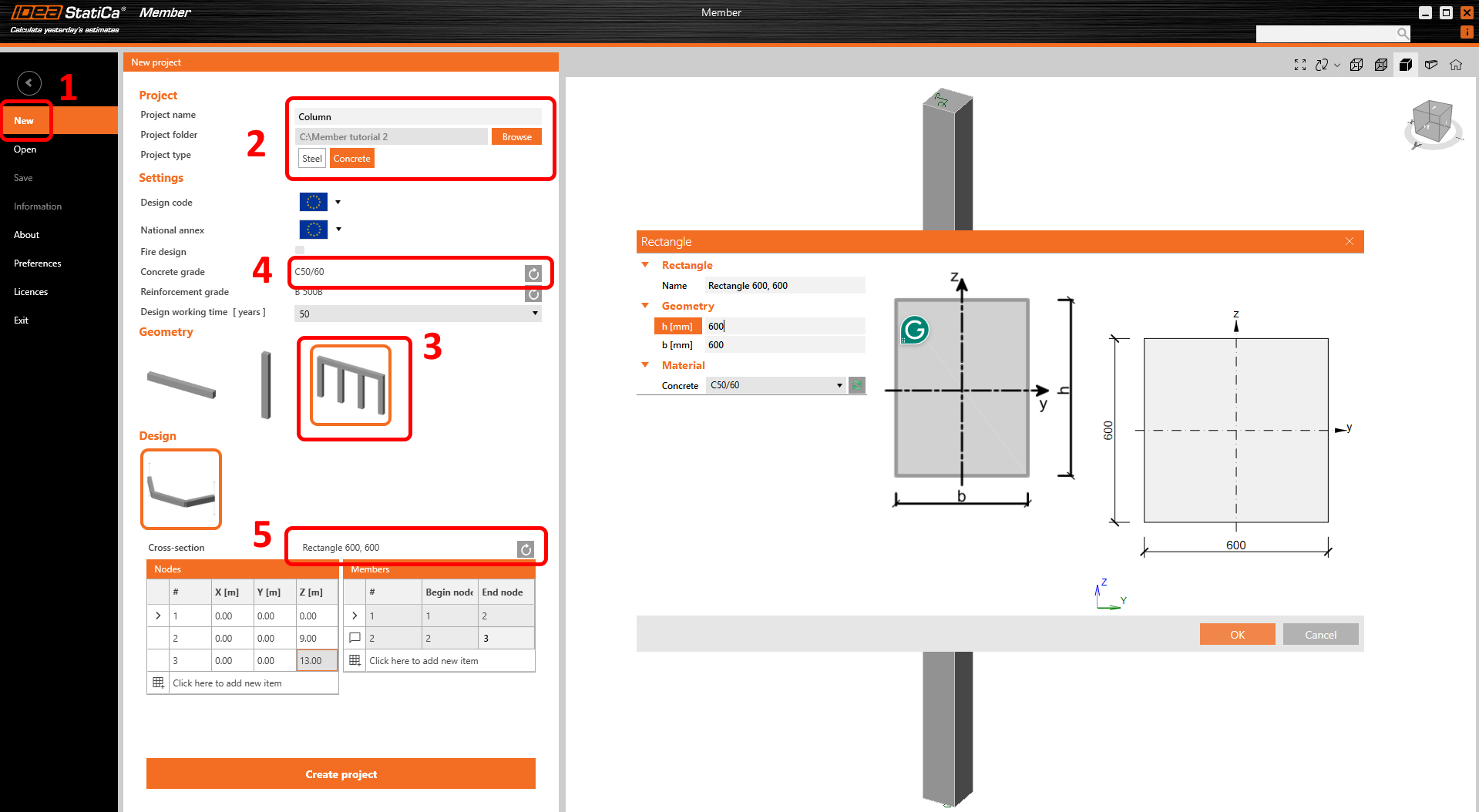
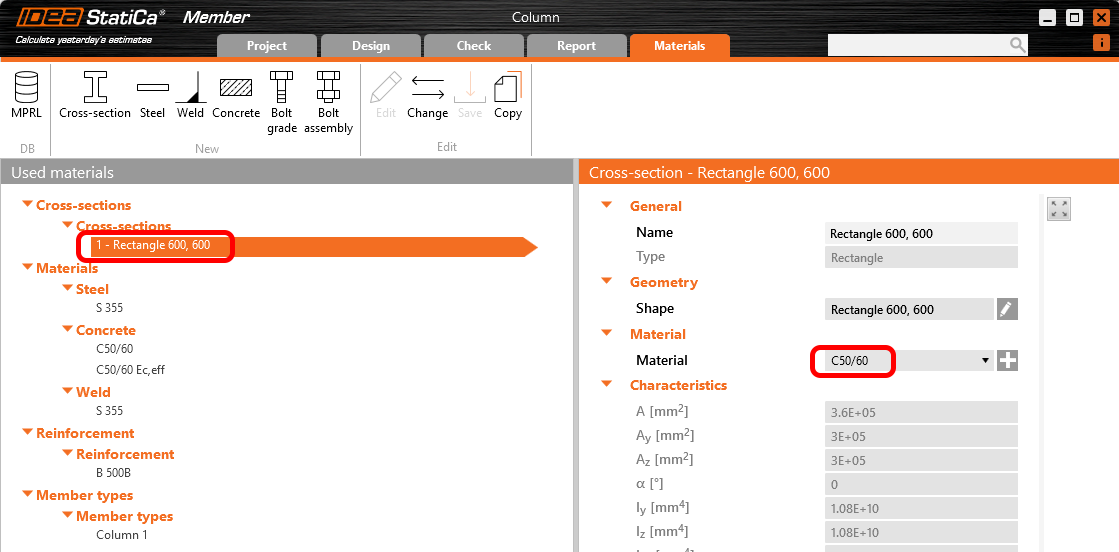
Vytvořte nový projekt (1), vyplňte jeho jméno a vyberte složku, kde bude projekt uložen (2). Poté nastavte typ projektu jako Beton (2) a zadejte typ geometrie obecný (3). Dále nastavte třídu betonu (4) na C50/60 a průřez sloupu (5) změňte po kliknutí na šipku na Obdélník 600, 600.

Sloup má odstupňovanou výztuž po délce a je proto potřeba ho modelovat dvojicí analyzovaných prutových prvků. Použijeme proto geometrii typu General, kde se geometrie modelu zadává pomocí tabulky. Nejprve zadejte souřadnice tří uzlů v levé tabulce. Poté přiřaďte uzly dvěma analyzovaným prvkům v pravé tabulce.

Nakonec klikněte na Vytvořit projekt.

3.2 Návrh

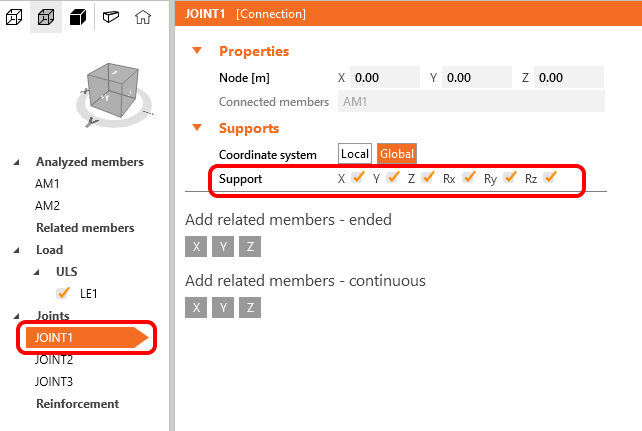
Pomocí šablony byl vygenerován model sloupu, který je potřeba zeditovat. Vyberte UZEL1 a zadejte podpory pro všech šest vnitřních sil - vetknutí sloupu. Následně vyberte UZEL3 (hlavu soupu) a všechny podpory vypněte.

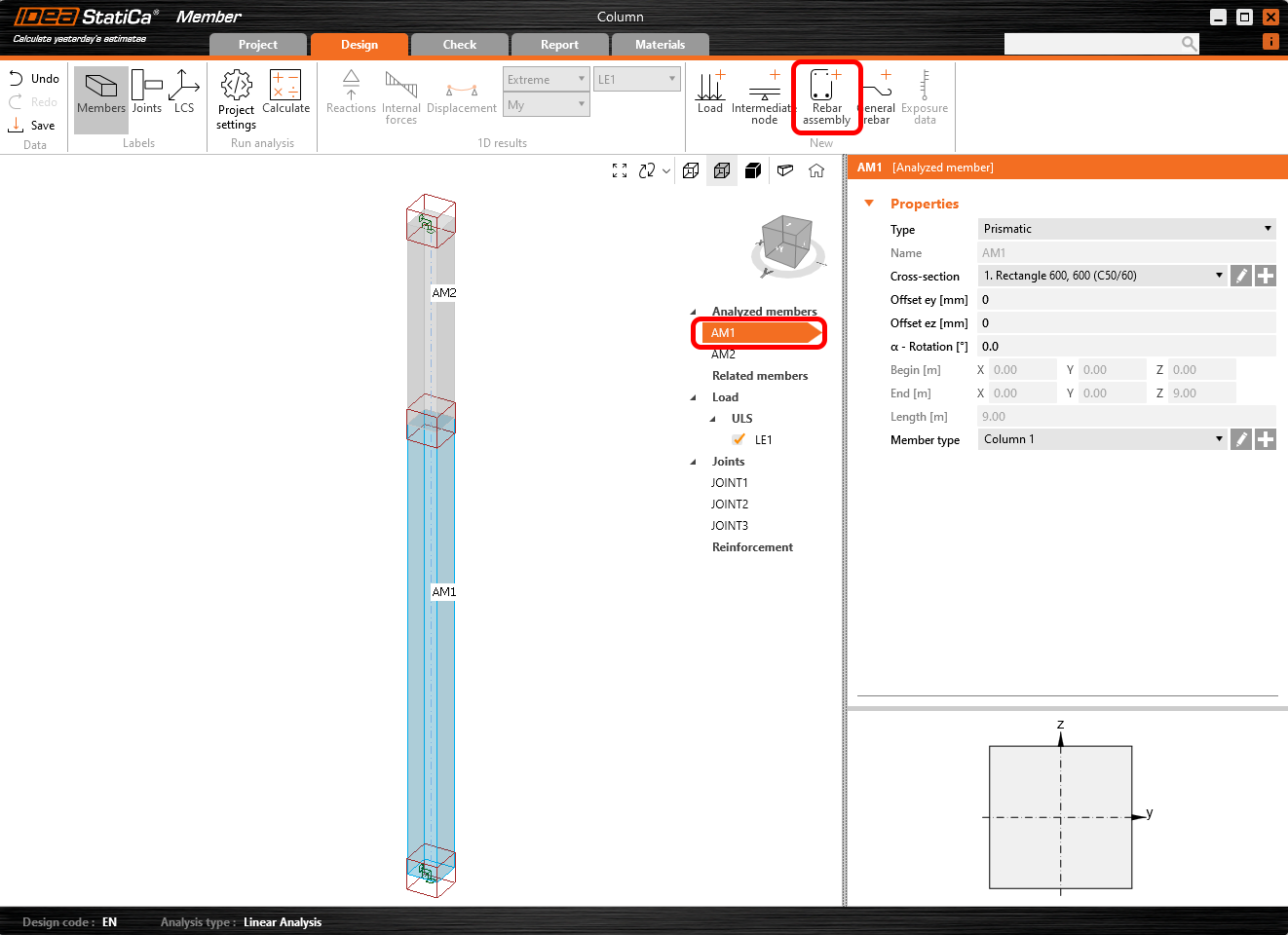
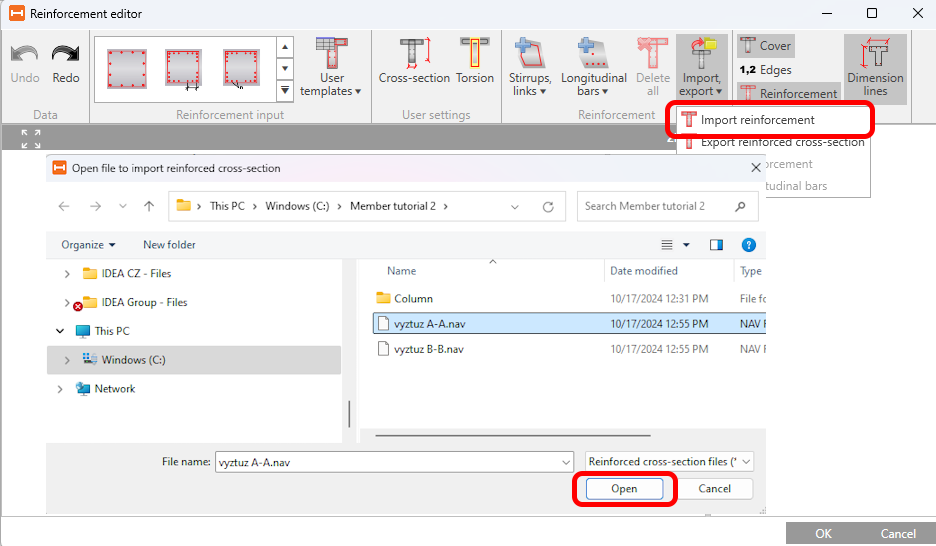
Dalším krokem bude definování výztuže. Vyberte Analyzovaný prvek AP1 a klikněte na tlačítko Sestava výztuže . Pro zadání výztuže použijte předpřipravenou šablonu reinf A-A.nav, která je ke stažení na konci návodu.

Obdobně pro analyzovaný prvek AP2 zadejte výztuž pomocí šablony reinf B-B.nav. Výsledkem je kompletní výpočtový model s vyztužením.

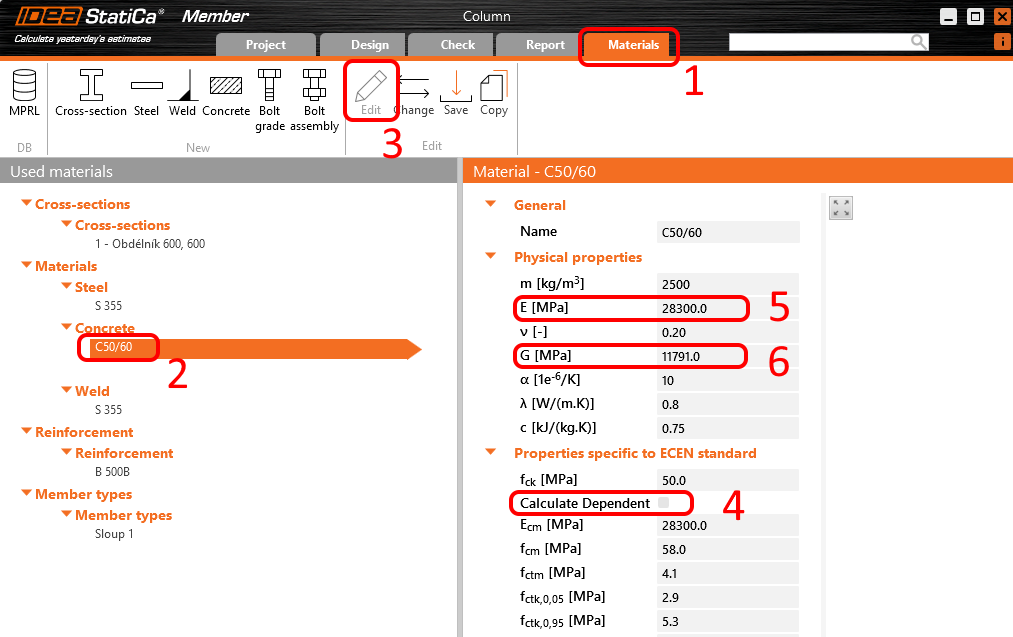
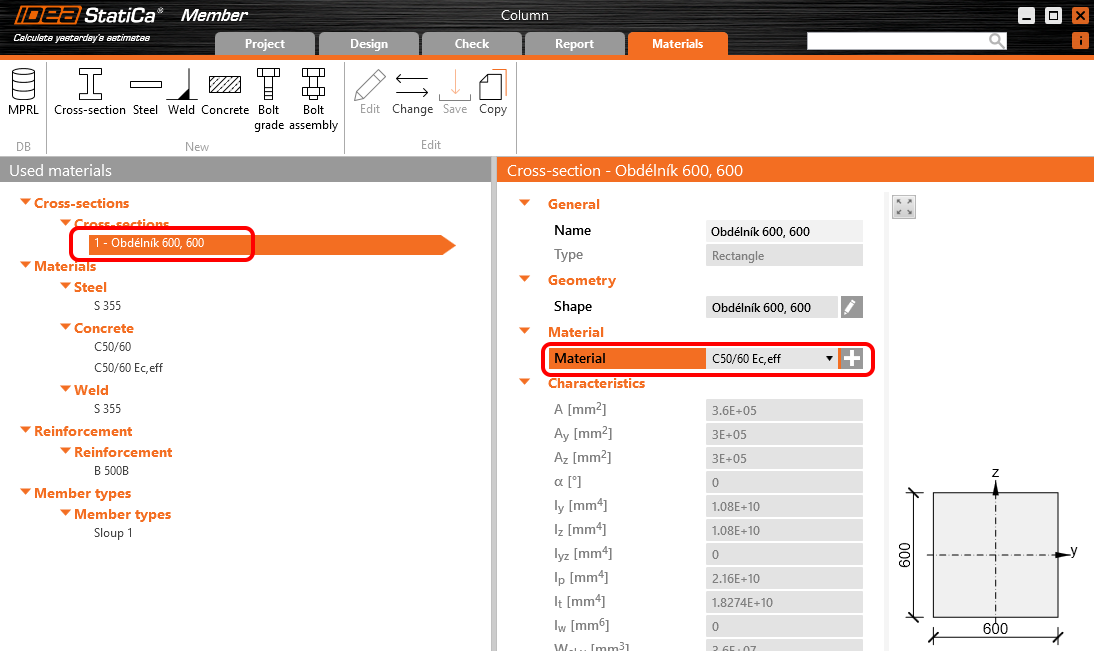
Charakteristická hodnota modulu pružnosti betonu je zadána hodnotou E_cm = 34 GPa. Je zřejmé, že na modulu pružnosti závisí velikost příčných deformací (a následně účinky II. řádu), které budeme vyčíslovat pro kvazistálou kombinaci  zatížení a vliv dotvarování betonu. Ve smyslu článku 5.8.6 (3), ČSN EN 1992-1-1 provedeme proto konzervativně redukci modulu pružnosti součinitelem γ_CE = 1.2 na hodnotu 28.3 GPa. Přepněte se do karty Materiály, vyberte beton C50/60 a klikněte na Upravit. Zrušte zaškrtnutí checkboxu Vypočítat závislé veličiny a přepište hodnotu modulu přužnosti E na 28300 MPa. Přepište také modul pružnosti ve smyku G na hodnotu vypočtenou ze vztahu G = E/2(1+ν) = 11791 MPa.

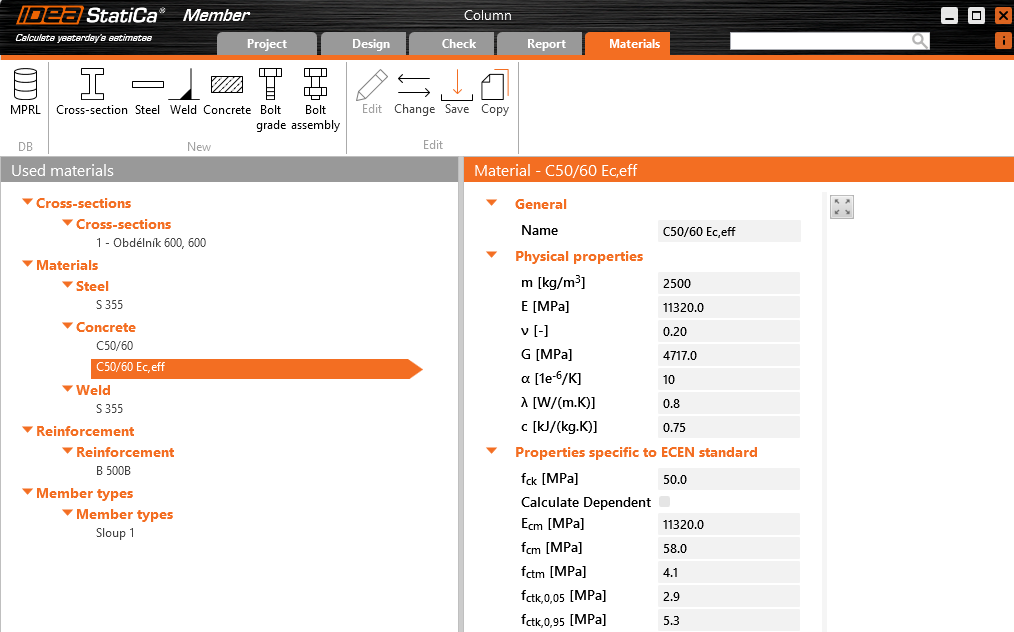
Dále si připravíme druhý materiál typu beton pro výpočet dlouhodobé deformace od kvazistálé kombinace. Beton C50/60 E_c,eff bude mít upravenou hodnotu modulu pružnosti na efektivní E_c,eff = E_c/(1+φ) = 28.3/(1+1.5) = 11.32 GPa. Původní materiál C50/60 zkopírujte pomocí tlačítka Kopírovat, nový materiál přejmenujte v kolonce Název na C50/60 E_c,eff a upravte hodnoty modulů pružnosti na  E = 11320 MPa a G = 4717 MPa dle postupu popsaného výše.

Dalším krokem je zadání zatížení. Program nepracuje se zatěžovacími stavy, ale zadávají se přímo kombinace zatížení. Zadáme jednu kombinaci zatížení ULS, jednu charakteristickou SLS_char a jednu kvazistálou  SLS_quasi. Zadávat budeme zatížení v hlavě sloupu a liniové zatížení reprezentující vlastní tíhu sloupu. Ohybové momenty se zadávají pomocí excentricity normálové síly. Nejprve zeditujeme kombinaci LE1. Nastavte typ zatížení, zadejte koncové síly a liniové zatížení dle obrázku níže.

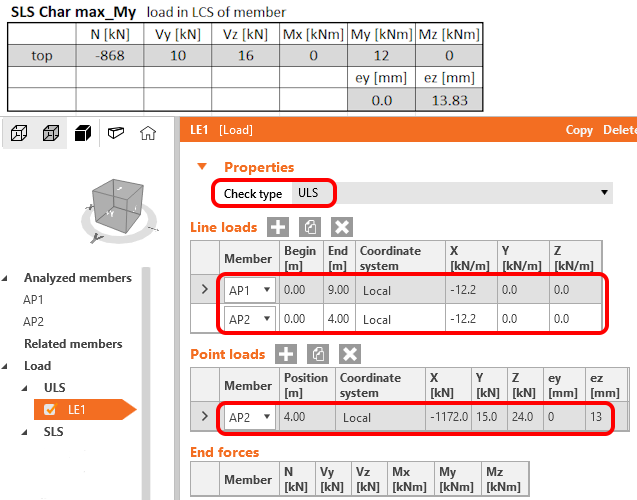
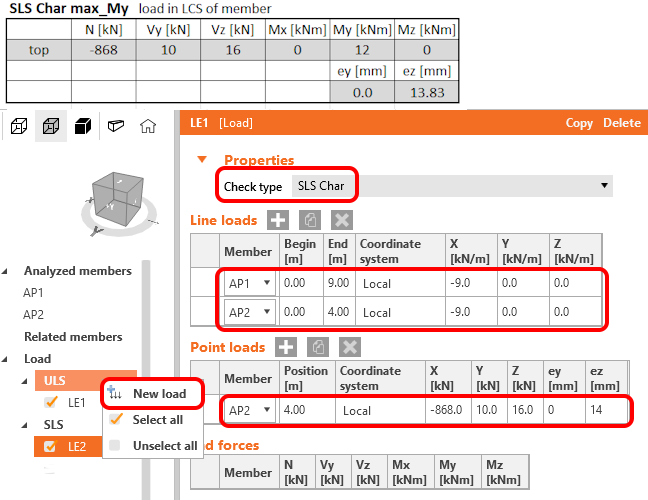
Pokračujte zadáním další kombinace LE2 - SLS char max_My. Klikněte pravým tlačítkem myši na nadpis ULS a zvolte Nové zatížení. Nastavte typ na SLS Char a vyplňte zatížení dle obrázku níže.

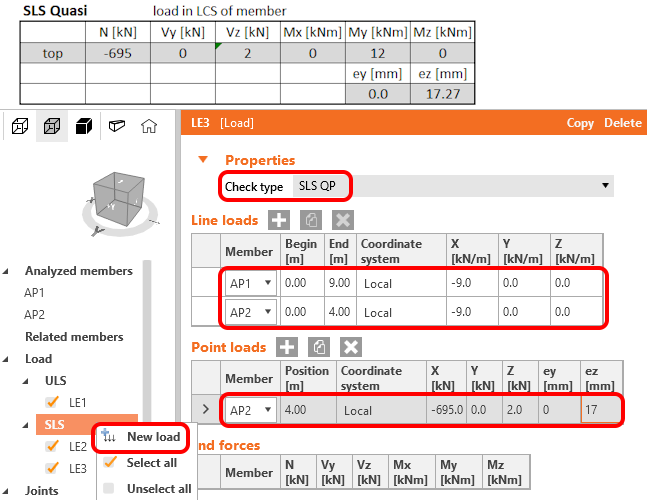
Jako poslední zadejte stejným způsobem kombinaci LE3  - SLS quasi.

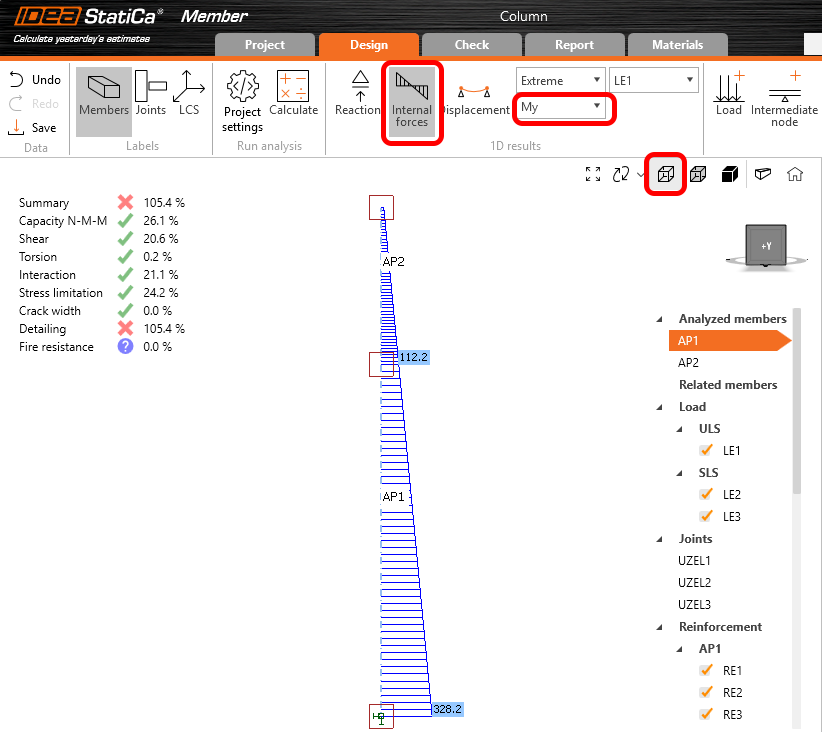
Model je nyní hotový, můžete na kartě Návrh kliknout na Vypočítat a provést lineární výpočet vnitřních sil. Vnitřní síly lze zobrazit kliknutím na ikonu Vnitřní síly a zkontrolovat soulad průběhu vypočtených vnitřních sil se zadanými vnitřními silami z globálního modelu. V kartě návrh se vyhodnocuje pouze lineární výpočet. Pro přehlednější vyhodnocení průběhů vnitřních sil je vhodné zapnot pouze osové schéma modelu pomoci ikony v horní liště hlavní scény.

Na obrázku níže je zobrazeno vyhodnocení vnitřních sil na kartě Posudek. Pro vyhodnocení lineární analýzy zde musí být navíc nastaven typ výpočtu na LA. 

3.3 Výpočet vlivu dotvarování na geometrickou imperfekci

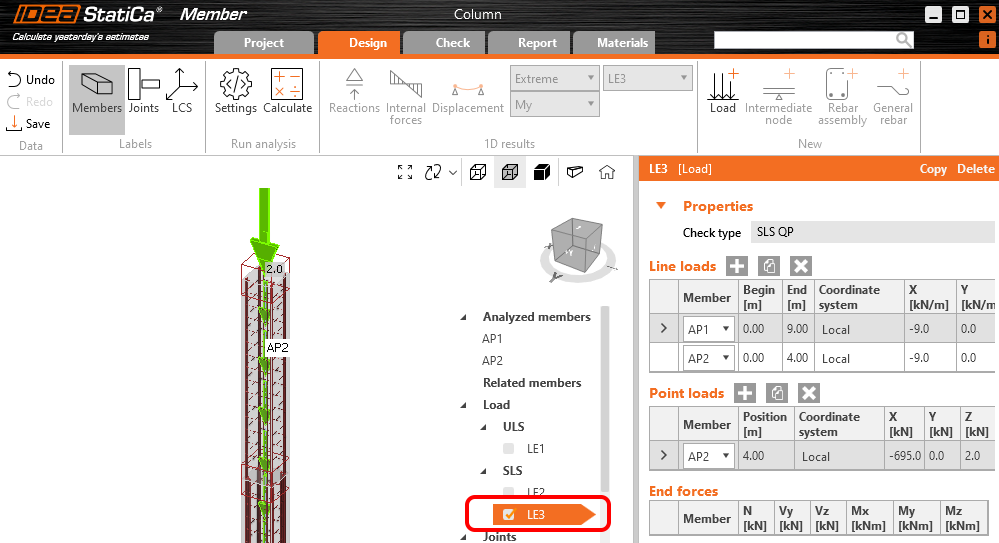
Nyní provedeme výpočet příčné deformace hlavy sloupu pro kvazistálou kombinaci LE3 v čase uvedení do provozu t₀ a na konci životnosti t_∞. Analyzovat budeme nyní jen kvazistálou kombinaci LE3, v seznamu kombinací nechte proto zaškrtnutou jen tuto kombinaci.

V kartě Materiál nejprve zkontrolujte, zda průžez sloupu má správně přiřazen materiál C50/60, který má nastaven modul pružnosti na E_cm = 28.3 GPa.

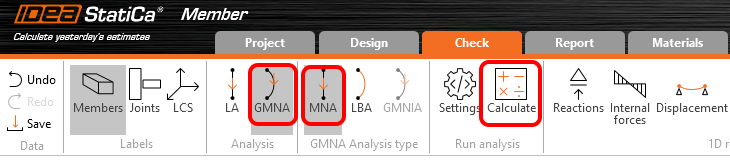
V kartě Posudek nastavte typ analýzy na GMNA. Po přepnutí na GMNA se automaticky nastaví první krok analýzy, to znamená MNA, materiálově nelineární analýza. Proveďte Výpočet.

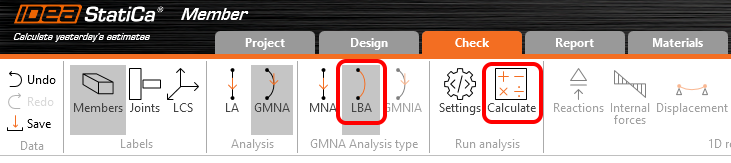
Přepněte se na druhý krok LBA (výpočet vlastních tvarů boulení) a spusťte Výpočet.

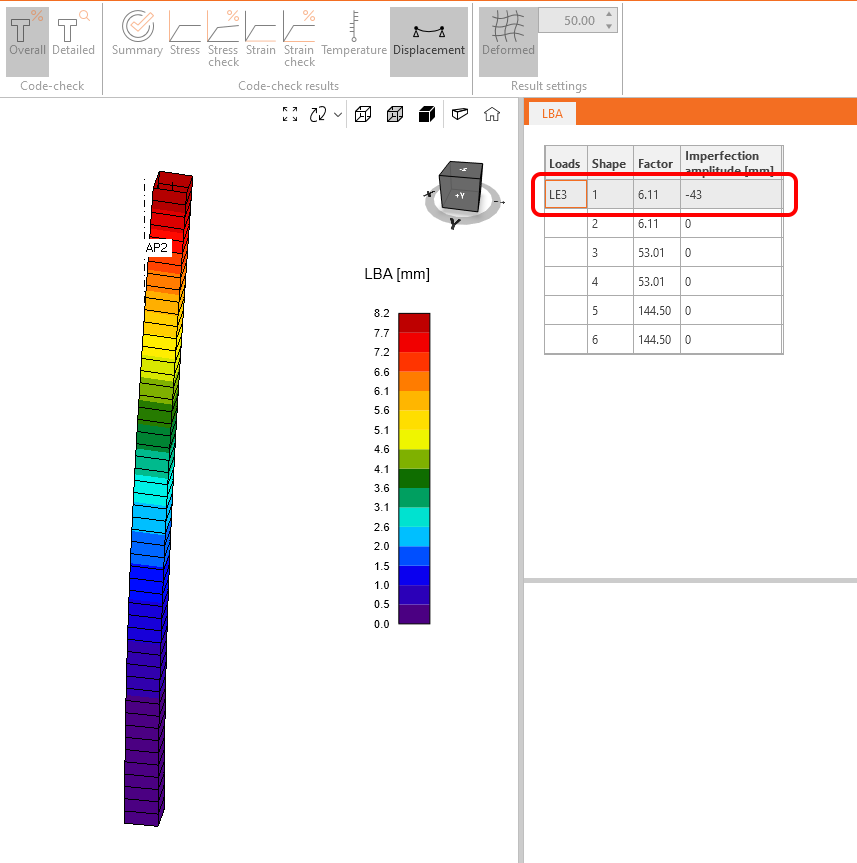
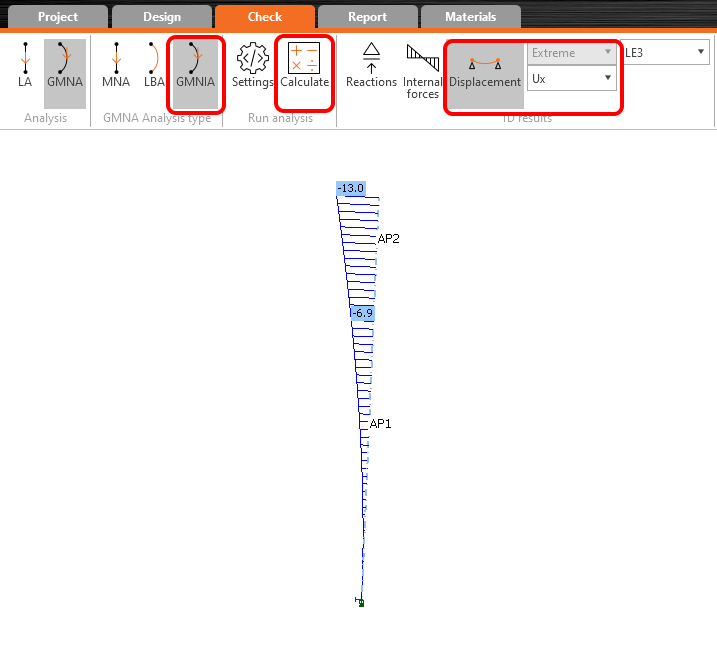
Pro zadání geometrické imperfekce využijeme první vlastní tvar boulení, kdy se hlava sloupu deformuje ve směru Z lokálního souřadného systému sloupu. Deformace hlavy sloupu u prvního tvaru vybočení je vykreslena v opačném směru než je deformace sloupu od kombinace LE3. Amplitudu imperfekce proto zadáváme se záporným znaménkem. To znamená -43 mm (viz kap. 1 Zadání).

Přepněte se na třetí krok - GMNIA, geometricky a materiálově nelineární analýzu s imperfekcí. Spusťte Výpočet. Nyní vyhodnotíme příčnou deformaci Ux v globálním souřadném systému modelu (ve směru Z v lokálním systému sloupu). Deformace od kvazistálého zatížení v čase t₀ je Ux = w_QP (t₀) = -13mm.

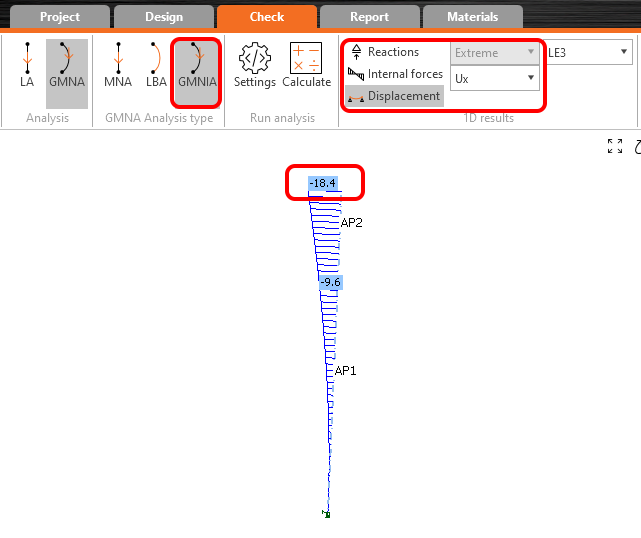
Nyní provedeme výpočet příčné deformace od LE3 v čase t_∞, na konci životnosti. Výpočet provedeme stejným způsobem, pouze změníme modul pružnosti sloupu na E_c,eff. Přepněte se do karty Materiály, vyberte průřez sloupu a změňte materiál na předpřipravený C50/60 Ec,eff.

Přepněte se zpět do karty Návrh a proveďte postupně všechny tři kroky analýzy. To znamená MNA, LBA (imperfekci ponecháme stejnou) a GMNIA. Vyhodnotíme příčnou deformaci Ux v globálním souřadném systému modelu (ve směru Z v lokálním systému sloupu). Deformace od kvazistálého zatížení v čase t_∞ je Ux = w_QP (t_∞) = -18.4 mm.

Přírstek geometrické imperfekce zohledňující vliv dotvarování od kvazistálých zatížení je potom

Δ e_i = w_QP (t_∞) - w_QP (t₀) = 18.4 - 13 = 5.4 mm

Celková geometrická imperfekce, kterou použijeme pro finální posouzení kombinace LE1 (mezního stavu únosnosti) je potom 43 + 5.4 = 48.4 mm. 

Výpočet deformace pomocí E_c,eff je pouze pomocný, přepněte materiál průřezu sloupu zpět na beton C50/60.

3.4 Posouzení ULS

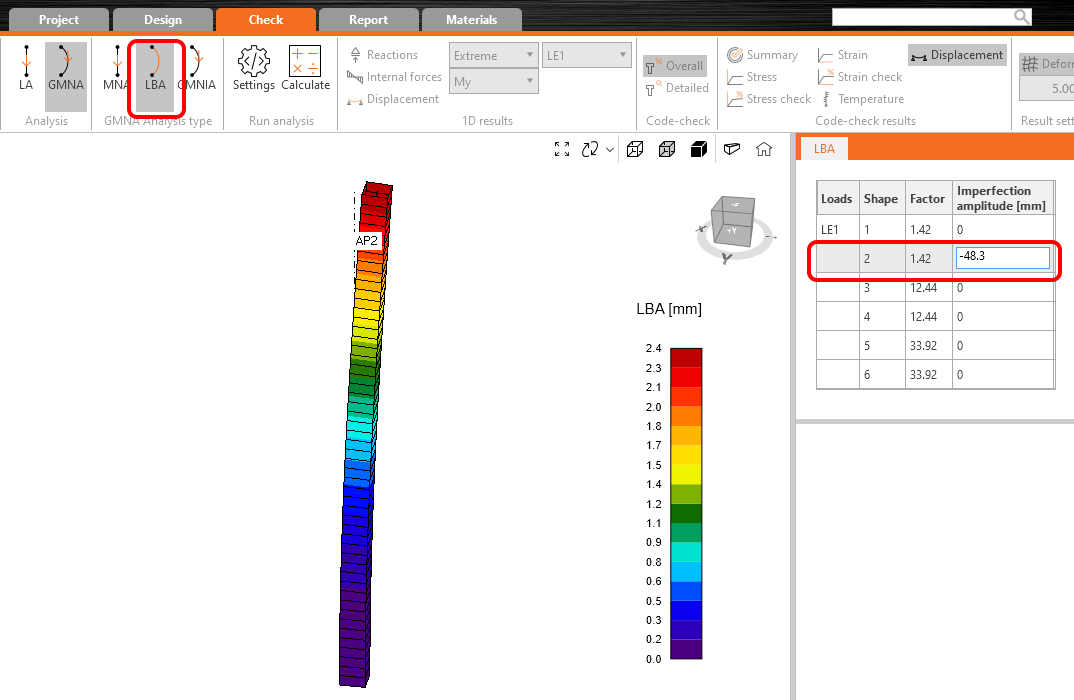
Zaškrtněte ve stromovém menu kombinaci ULS - LE1 pro finální posouzení únosnosti sloupu. Proveďte MNA výpočet a následně LBA výpočet. Pro zadání imperfekce tentokrát musíme použít druhý tvar vybočení. Hlava sloupu se deformuje ve směru Z lokálního souřadného systému sloupu. Celkovou imperfekci zadáme hodnotou -48.4 mm.

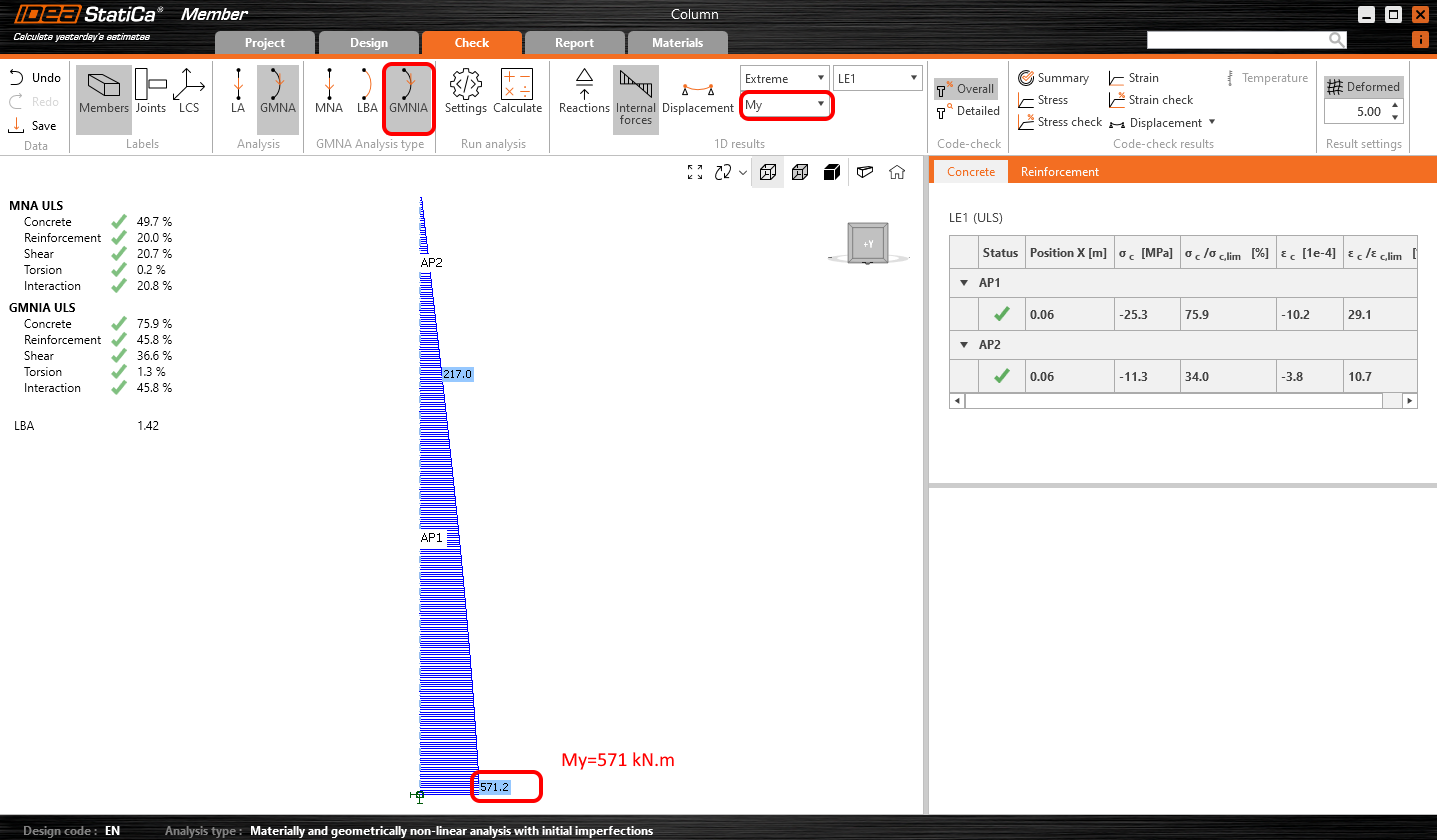
Proveďte poslední krok analýzy - výpočet GMNIA. Jako první provedeme vyhodnocení ohybu sloupu.  Rozhodující pro namáhání průřezu je moment My ve vetknutí sloupu, který při MNA analýze (bez vlivu II. řádu) vyšel 328 kNm. Moment vypočtený pomocí GMNIA je 571 kNm. Je vidět, že vliv II. řádu je u řešeného sloupu zásadní.

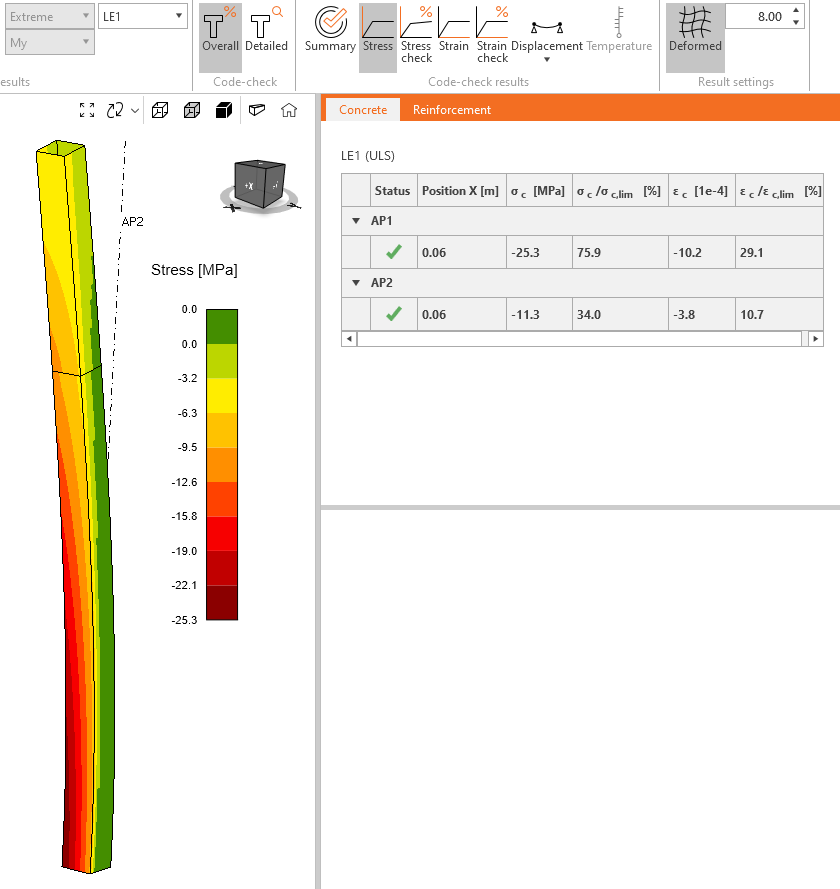
Dalé vyhodnotíme napětí v betonu a výztuži. Nejprve na celém modelu a následně v rozhodujícím průřezu. Vyberte Souhrnný posudek v horním pásu a Napětí pro zobrazení napětí v betonu sloupu. Zelená oblast sloupu ve scéně představuje část betonového průřezu, který byl namáhán tahem a byl při analýze vyloučen z průřezu. V tabulce výsledků vpravo jsou potom uvedena maximální napětí a poměrná přetvoření, která jsou porovnána s limitními hodnotami poměrných přetvoření definovaných návrhovou normou (dle metody mezních přetvoření).

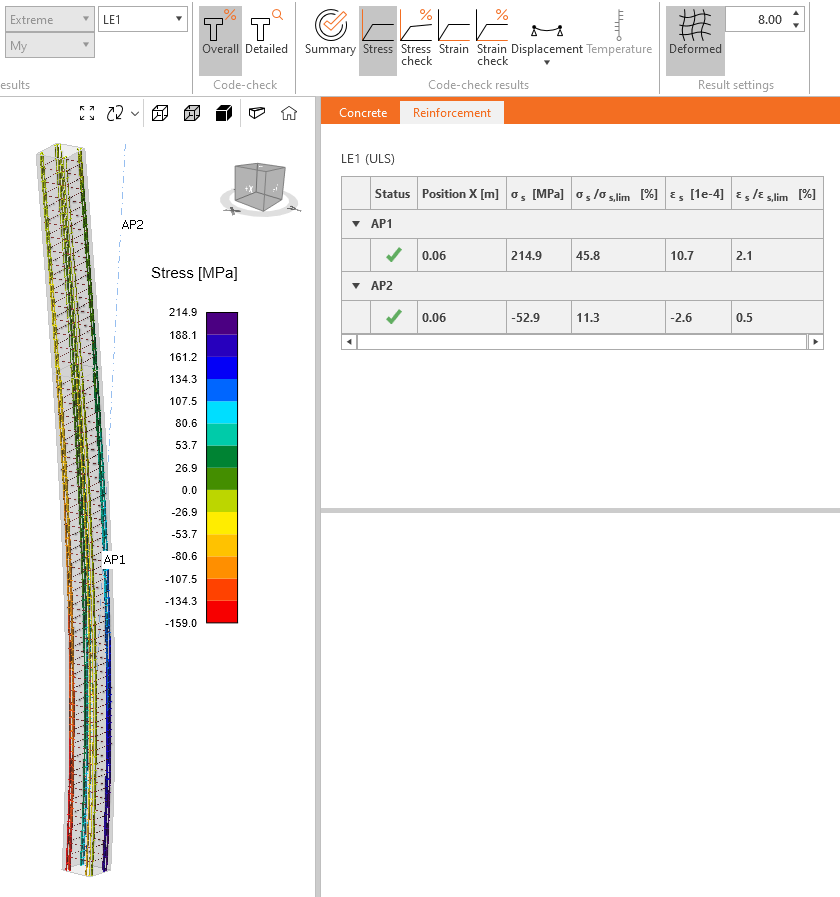
Kliknutím na Výztuž v záhlaví tabulky výsledků pak zobrazíte normálová napětí ve výztuži. Opět jsou v tabulce vpravo uvedena maximální napětí a přetvoření.

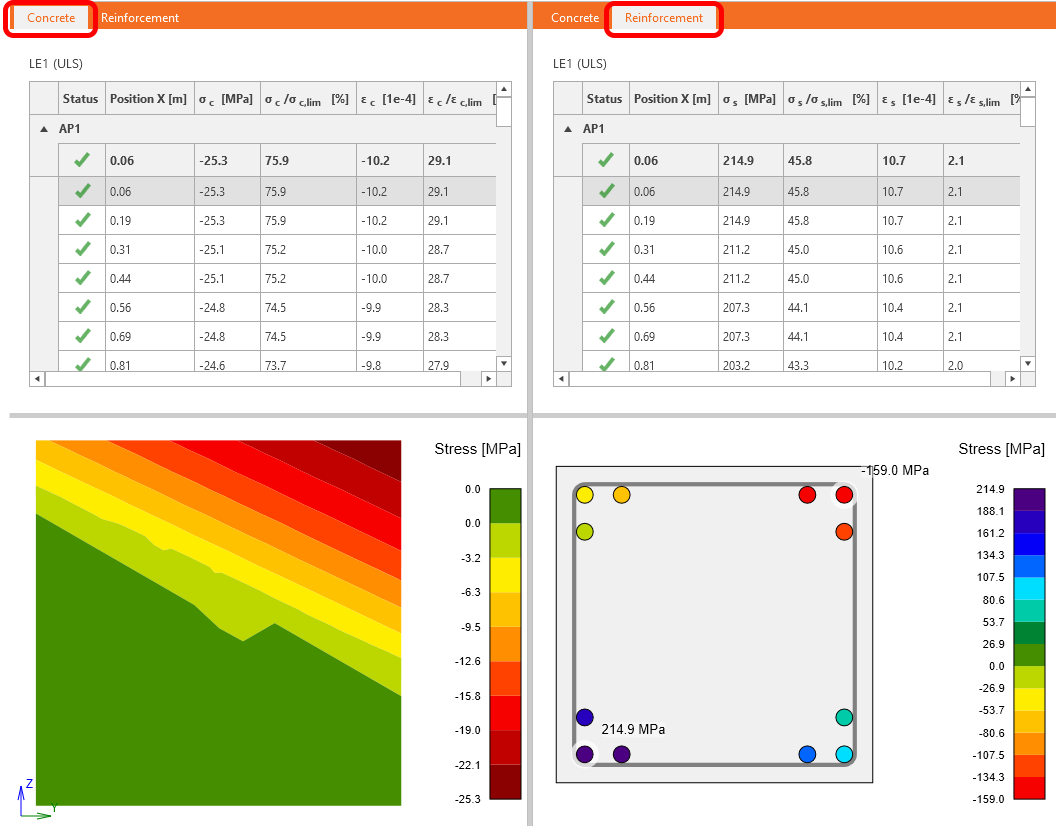
Výsledy analýzy lze rovněž zobrazit detailně pro kritický (nebo libovolně vybraný) průřez sloupu. V horním pásu karet vyberte Detailní posouzení a ve scéně vyberte příčný řez, který chcete vyhodnotit. V našem případě je rozhodující spodní průřez u vetknutí sloupu. Stejně jako u souhrnného posouzení se výsledky přepínají v betonu a ve výztuži.

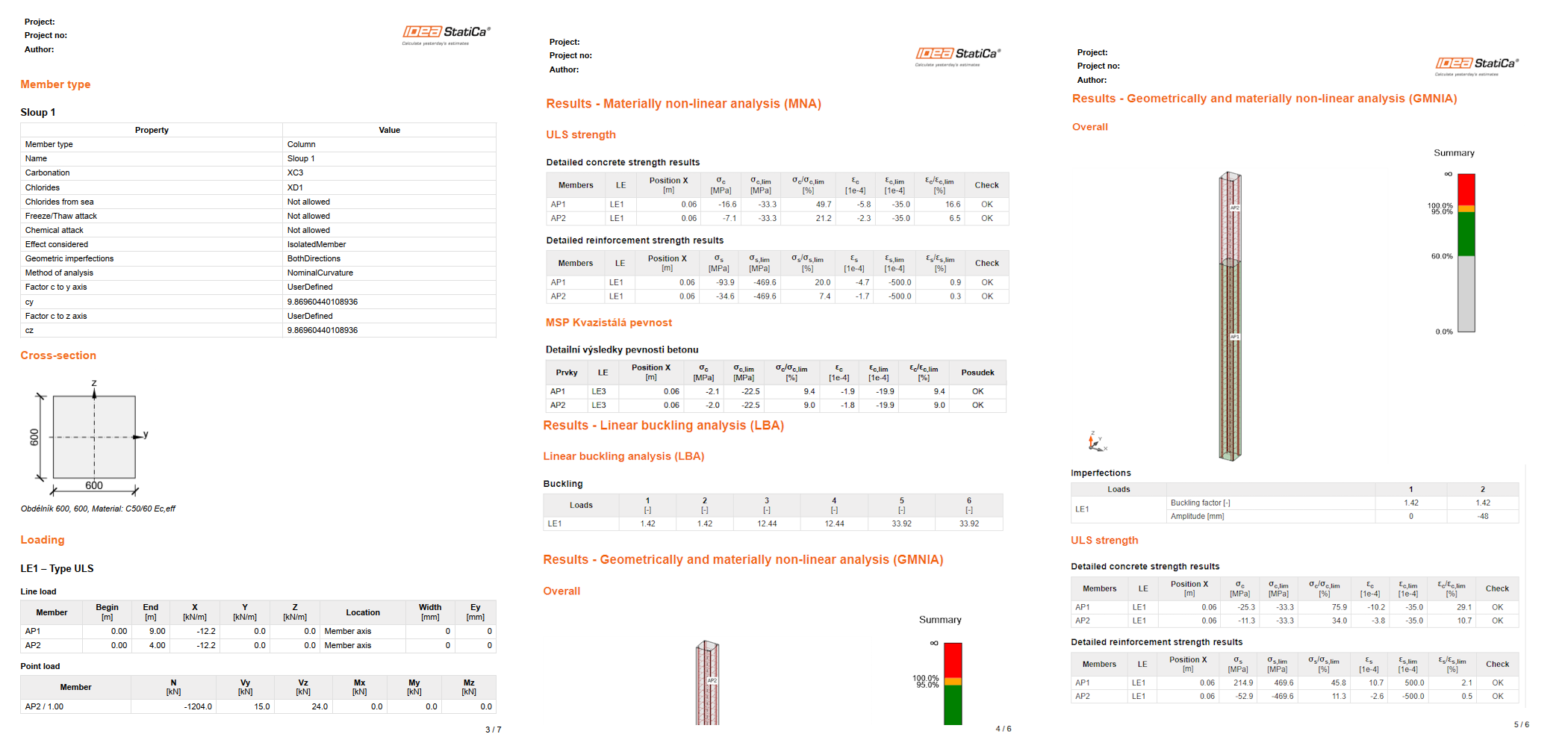
3.5 Protokol

Pro vygenerování protokolu o výpočtu se přepněte do karty Report v horním pásu karet a poté klikněte na ikonu Generovat.