In der Praxis werden für die Bemessung von Diskontinuitätsbereichen in Stahl- und Spannbetontragwerken üblicherweise das Fachwerkmodell (Strut and Tie Method, S&T) und die Spannungsfeldmethode verwendet. Die Compatible Stress Field Method (CSFM) wurde durch die Erweiterung dieser klassischen Theorien entwickelt und ermöglicht einen hohen Automatisierungsgrad und steht im Einklang mit den Bemessungsnormen. Trotz ihrer Einfachheit liefert die Methode eine sehr realistische Beschreibung des Tragverhaltens sowohl im Grenzzustand der Tragfähigkeit (GZT) als auch im Grenzzustand der Gebrauchstauglichkeit (GZG). Das CSFM ist in IDEA StatiCa Detail implementiert.
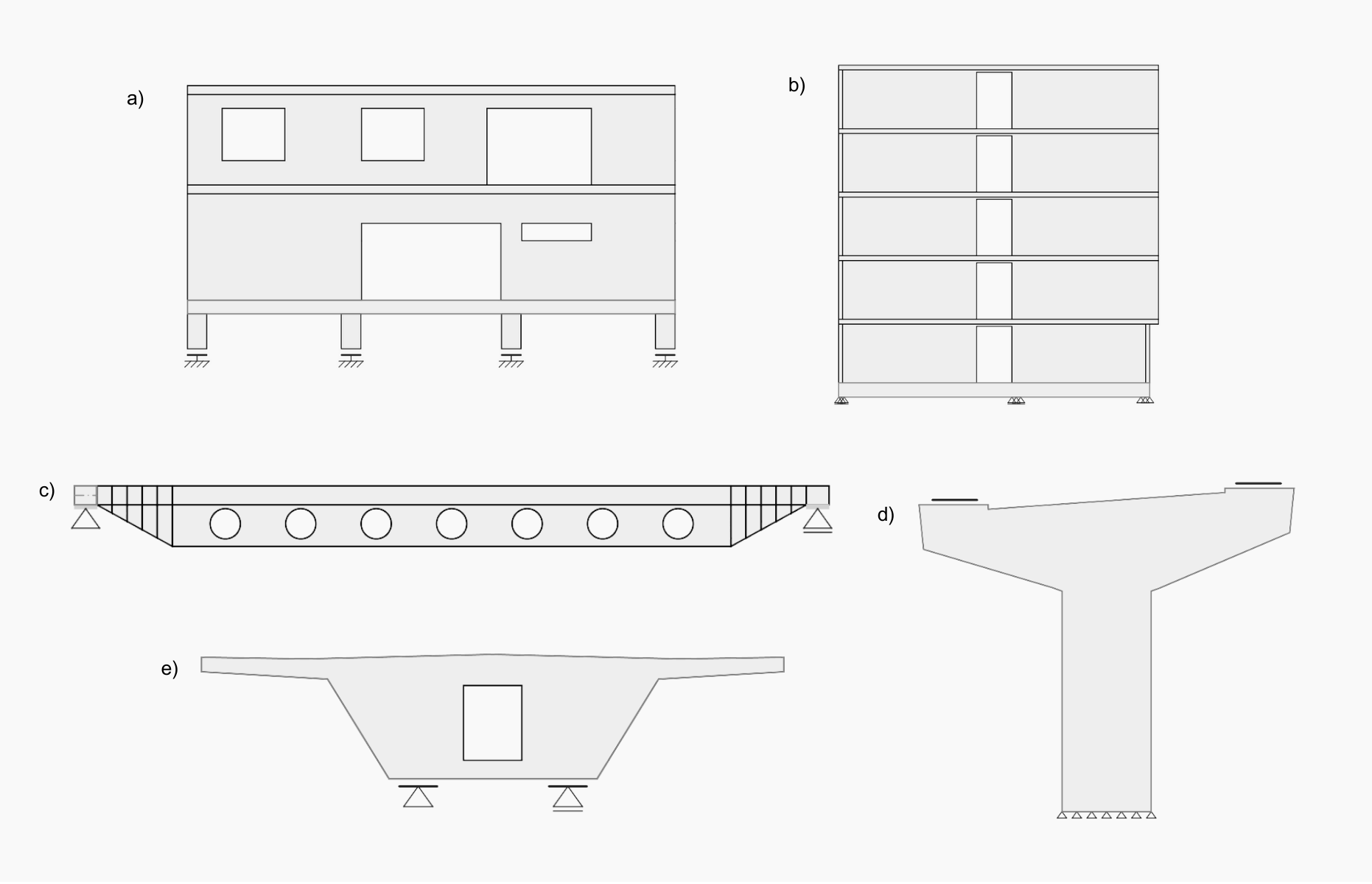
Abb. 1 a) Wand mit Öffnungen b) Schubwand c) Träger mit gestuften Enden und Öffnungen d) Brückenpfeiler e) Brückenmembran
Die Standardverfahren für die Bemessung von Betonquerschnitten sind in den Bereichen anwendbar, in denen die Bernoulli-Navier-Hypothese der ebenen Spannungsverteilung gilt (Bereich B). Die Stellen, an denen diese Hypothese nicht zutrifft, werden als Diskontinuitätsbereiche (D-Bereiche) bezeichnet. Dazu gehören Teile von Bauwerken, in denen konzentrierte Lasten auftreten oder in denen eine plötzliche Querschnittsveränderung auftritt, wie z. B. gestufte Enden (Abb. 1c), tiefe Balken, Wände mit Öffnungen (Abb. 1a, 1b) oder Pfahlköpfe. Im Brückenbau sind dies z. B. Widerlagerwände mit Öffnungen, Pfahlkopfplatten usw.
1. Fachwerkmodell
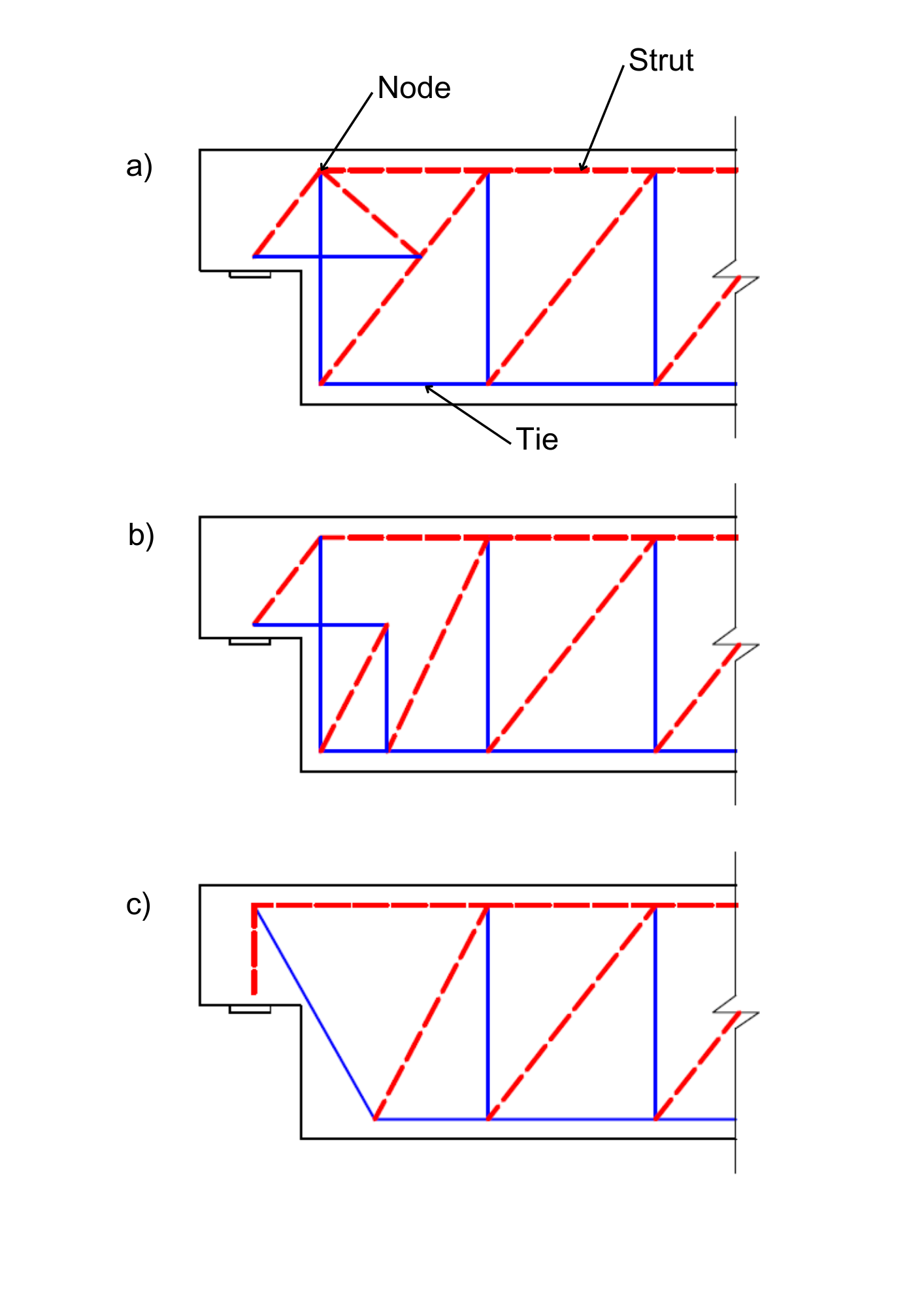
Die Grundannahme bei der Definition eines S&T-Modells ist, dass die Zugfestigkeit des Betons vernachlässigt wird. Ein einfaches Fachwerkmodell besteht aus Elementen, die auf Druck und Zug wirken und das GZT-Verhalten darstellen. Im Allgemeinen ist dies kein komplexes Problem, und die Definition eines grundlegenden S&T-Modells (Abb. 2a) sollte für einen erfahrenen Ingenieur kein Problem darstellen. Doch selbst bei dieser grundlegenden Aufgabe kann die korrekte Bewertung des Modells in Übereinstimmung mit der Entwurfsnorm ein langwieriger, manueller und iterativer Prozess sein.
Abb. 2 a) S&T-Modell Option 1 b) S&T-Modell Option 2 c) S&T-Modell Option 3
Verankerungen, Knotenbereiche und Querdehnungen in den Streben müssen bewertet werden. Wenn das Modell die Prüfung nicht besteht, muss eine S&T Geometrie angepasst oder ein anderes S&T Modell gewählt werden (Abb. 2b, 2c). Dies führt häufig dazu, dass der Tragwerksplaner die S&T Modellgeometrie nur einmal auswählt und nur den Bewehrungsstab bewertet. Dies kann zu einem erheblichen Fehler führen. Die Wahl des Modells ist immer eine Frage der Erfahrung. Bei komplexeren Strukturdetails ist die Wahl eines S&T-Modells, das dem tatsächlichen Verhalten der Struktur ausreichend entspricht, nicht immer so einfach wie im obigen Fall. Außerdem ist die S&T nur eine Methode für den Entwurf von Grenzzuständen der Tragfähigkeit. Sie ermöglicht nicht die Bemessung von Grenzzuständen der Gebrauchstauglichkeit (Verformung, Rissbildung), die insbesondere bei Bauwerken von erheblicher Bedeutung kritische Nachweise sind, da sie sich direkt auf die Lebensdauer des Bauwerks auswirken.
2. Kompatible Spannungsfeldmethode - CSFM
CSFM ist eine moderne nichtlineare Methode für die Analyse von D-Regionen und Elementen, deren Verhalten auf eine ebene Spannung vereinfacht werden kann, d. h. ein 2D-Modell. Sie basiert jedoch immer noch auf einer grundlegenden und sicheren Annahme der Normen: Beton wirkt nicht auf Zug, und alle Spannungen müssen durch Bewehrung übertragen werden. Die kompatible Spannungsfeldmethode (CSFM) ist eine Weiterentwicklung der S&T- und der Spannungsfeldmethode und beseitigt deren oben genannte Hauptnachteile: Unsicherheiten bei der Modellauswahl, Schwierigkeiten bei der Automatisierung und die Unmöglichkeit, Grenzzustände der Gebrauchstauglichkeit zu bewerten.
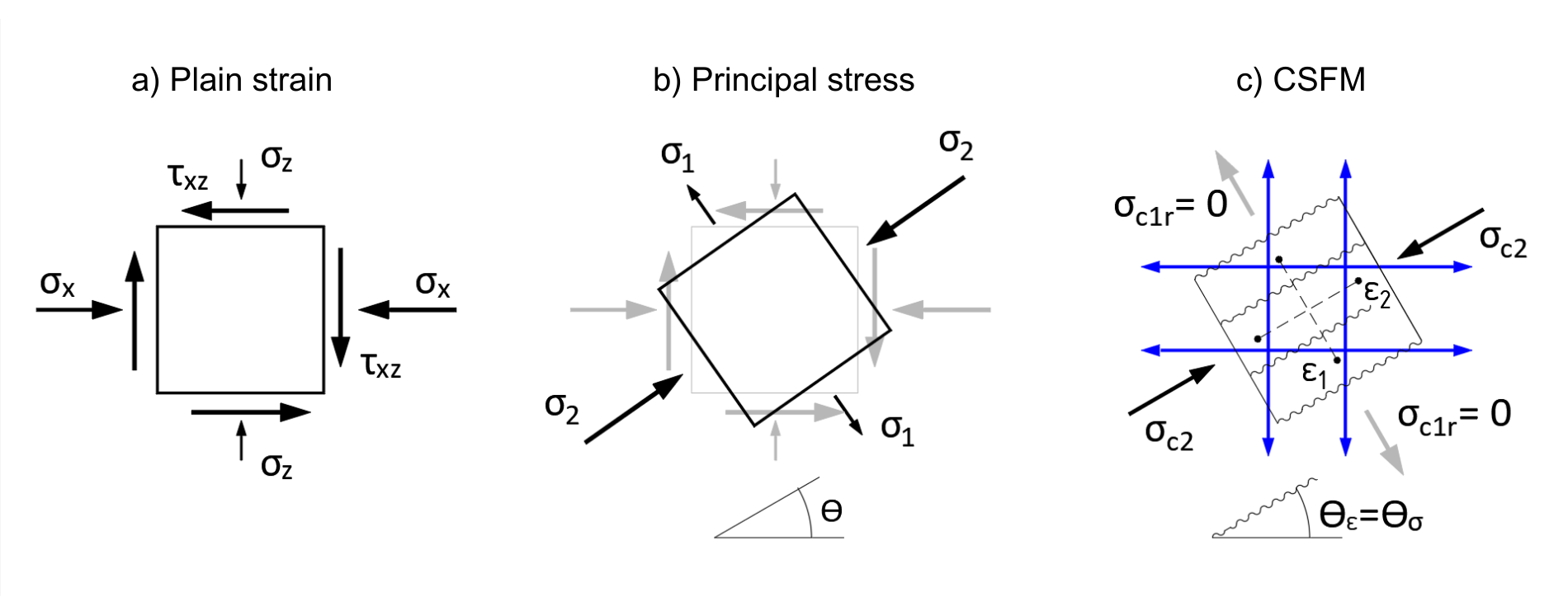
Abb. 3 a) Normale Dehnung b) Hauptspannung c) CSFM
Das Prinzip der CSFM kann anhand der ebenen Spannung des Grundelements einer Stahlbetonstruktur erklärt werden. Abb. 3a zeigt das 2D-Basiselement in ebener Spannung, wie wir es aus allen Lehrbüchern kennen. Dabei handelt es sich um die Spannung an einem Punkt der Struktur, die beispielsweise durch eine linear-elastische Analyse mit Hilfe der Finite-Elemente-Methode (FEM) ermittelt wird. Das Element ist einer horizontalen Normalspannung σx, einer vertikalen Normalspannung σz und einer Schubspannung τxz ausgesetzt. Aus diesen Spannungen lassen sich die sogenannten Hauptspannungen und ihre durch den Winkel θ definierte Richtung bestimmen (Abb. 3b). Das Element wird dann mit der Hauptzugspannung σ1 und der Hauptdruckspannung σ2 belastet.
Wie sieht die Dehnung desselben mit CSFM analysierten Elements aus? Die Dehnung ist in Abbildung 3c dargestellt. Der gestauchte Beton erscheint in der Richtung der Hauptdruckspannung σ2. Und es wird ein Spannungsfeld mit der Spannung σc2 erzeugt. Wie bereits erwähnt, ist die Grundannahme, dass der Beton nicht auf Zug beansprucht wird. Daher wird die transversale Hauptzugspannung σ1 vom Beton nicht übertragen, und es bildet sich ein Riss senkrecht zu dieser Richtung. Die Spannung σc1r muss daher gleich Null sein. Um das Versagen unseres 2D-Elements zu vermeiden, müssen alle Zugspannungen durch die Bewehrung übertragen werden (in Abb. 3c blau dargestellt), die Teil des Berechnungsmodells sein muss.
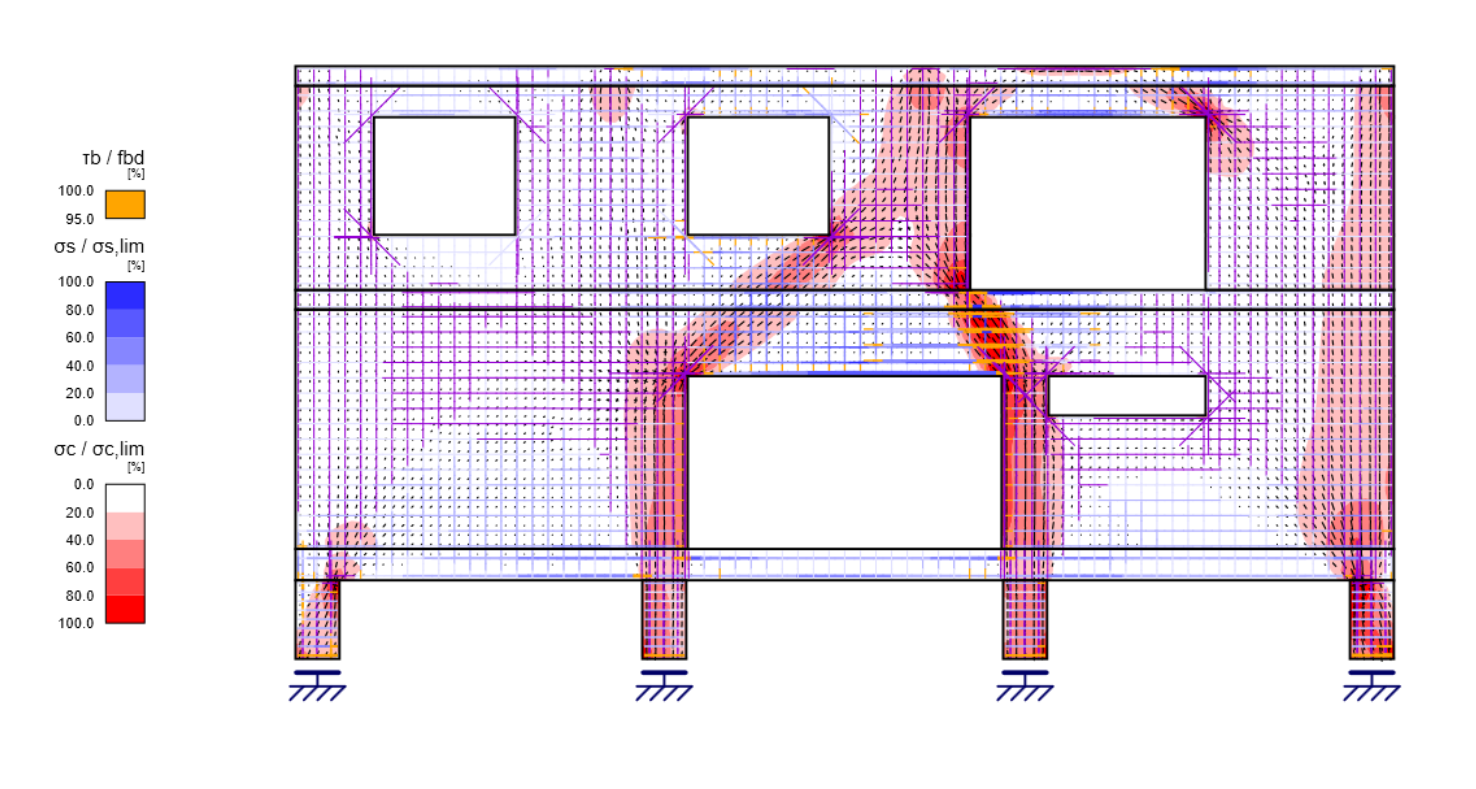
Wenn diese Spannungsanalyse mit CSFM kontinuierlich über den gesamten zu lösenden 2D-Bereich durchgeführt wird, ergibt sich ein kontinuierliches Druckfeld im Beton plus Zug- und Druckspannungen in der Bewehrung. Eine vereinfachte grafische Darstellung des CSFM-Spannungsfeldes ist in Abbildung 4 zu sehen. Zusätzlich zu den Ausnutzungsgraden von Beton und Bewehrung zeigt die Abbildung auch die unterschiedlichen Richtungen der berechneten Spannungen σc2 entlang der Regionen.
Abb. 4 Gesamtergebnisse aus IDEA StatiCa Detail
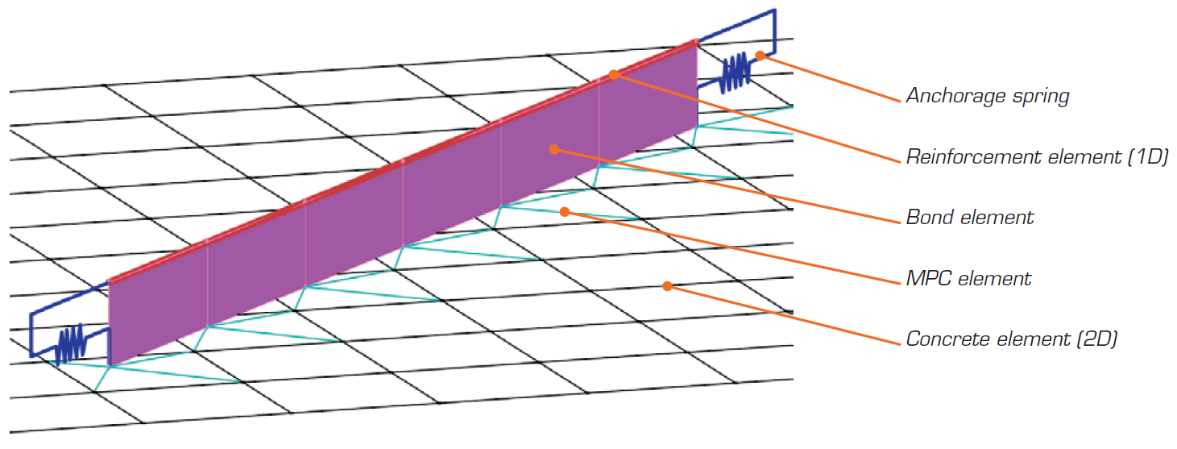
Die Analyse eines Details oder einer Struktur mit CSFM basiert auf der Methode der finiten Elemente. Der Beton wird mit 2D-Wandelementen modelliert, die Bewehrung mit 1D-Stabelementen (Abb. 7). Die Analyse wird nicht in einem Schritt durchgeführt, da es sich um ein nichtlineares Problem handelt. Die Lasten werden während der Berechnung schrittweise aufgebracht, und die Lösung des nichtlinearen Gleichungssystems wird mit der Newton-Raphson-Methode gefunden.
Die fiktiven verschmierten Risse (ε1 ist der Mittelwert) werden senkrecht zur Richtung der Hauptspannungen "gebildet", die sich während der nichtlinearen Berechnung ändern können, da das Element bei jedem Belastungsinkrement "progressiv reißt". Zusammenfassend wird ein fiktiver spannungsfreier rotierender Riss betrachtet.
Das Ergebnis der FEM-Lösung mit CSFM ist ein kompatibles Spannungsfeld (d.h. der Beton zerfällt im Modell nicht in einzelne, unabhängig voneinander wirkende Streben) und der Dehnungszustand, die über den gesamten zu lösenden 2D-Bereich kontinuierlich sind. Dies ist ein großer Vorteil gegenüber klassischen S&T-Ansätzen und ermöglicht die Automatisierung und Verfeinerung des Berechnungsmodells, wie in den folgenden Abschnitten beschrieben.
Abb. 5 Prinzip der Betonerweichung
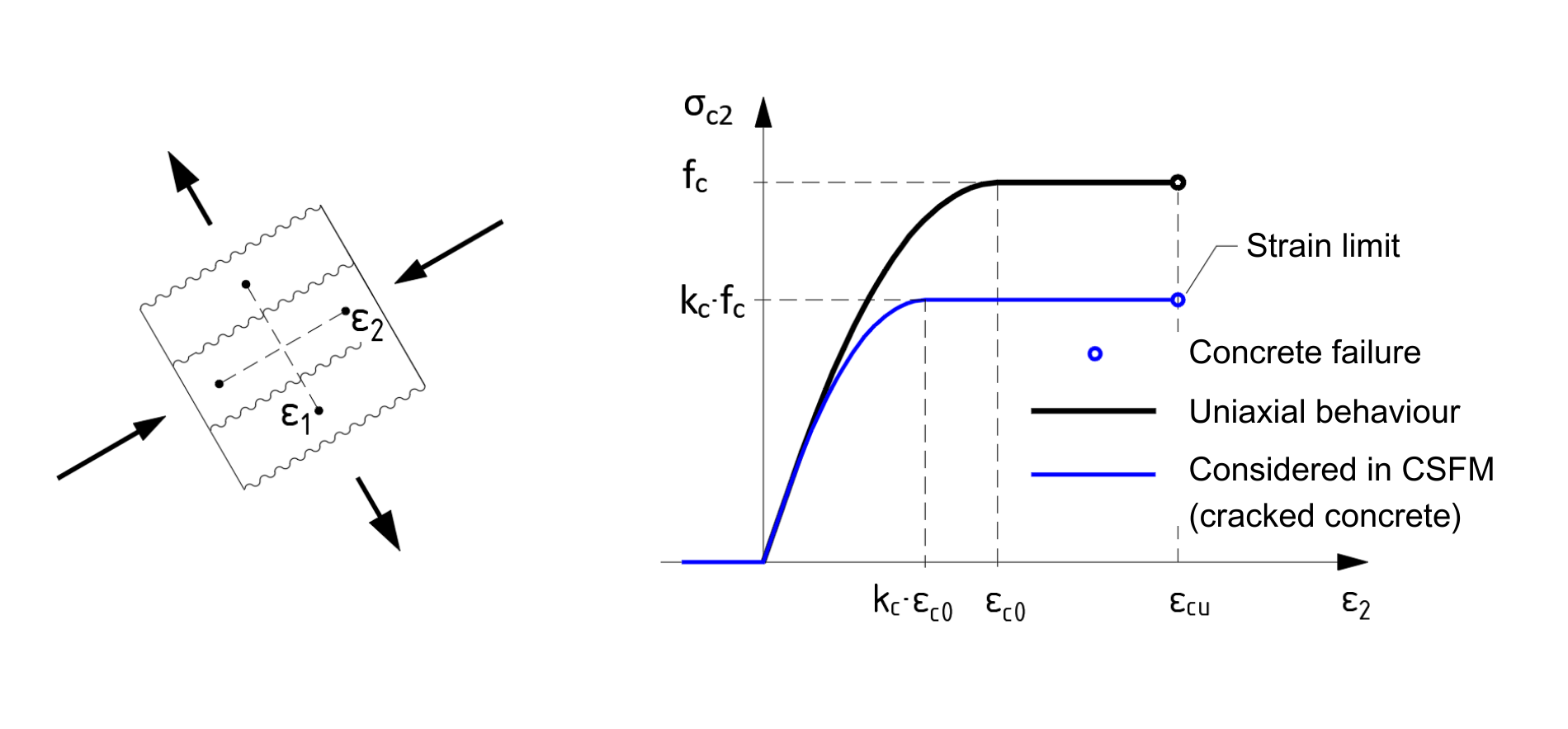
Die einfache Formulierung des CSFM ermöglicht die Verwendung des standardmäßigen einachsigen parabolisch-rechteckigen Spannungs-Dehnungs-Diagramms für Beton unter Druck entsprechend der Bemessungsnorm. Bekanntlich nimmt die Druckfestigkeit von Beton ab, wenn der Beton durch Querrisse geschädigt wird (Abb. 5). Dieser so genannte Druckentlastungseffekt wird in dem Verfahren durch die automatische Berücksichtigung der effektiven Druckfestigkeit des Betons berücksichtigt.
Ausgehend von der Höhe der Querzugspannungen ε1 wird der Abminderungsfaktor kc bestimmt und das Spannungs-Dehnungs-Diagramm des Betons angepasst (Abb. 5). Da das Feld der Dehnungen im gesamten Bauwerk bekannt ist, kann die effektive Druckfestigkeit des Betons in einzelnen Abschnitten in Abhängigkeit vom lokalen Niveau der Querzugdehnungen ε1 automatisch berechnet werden.
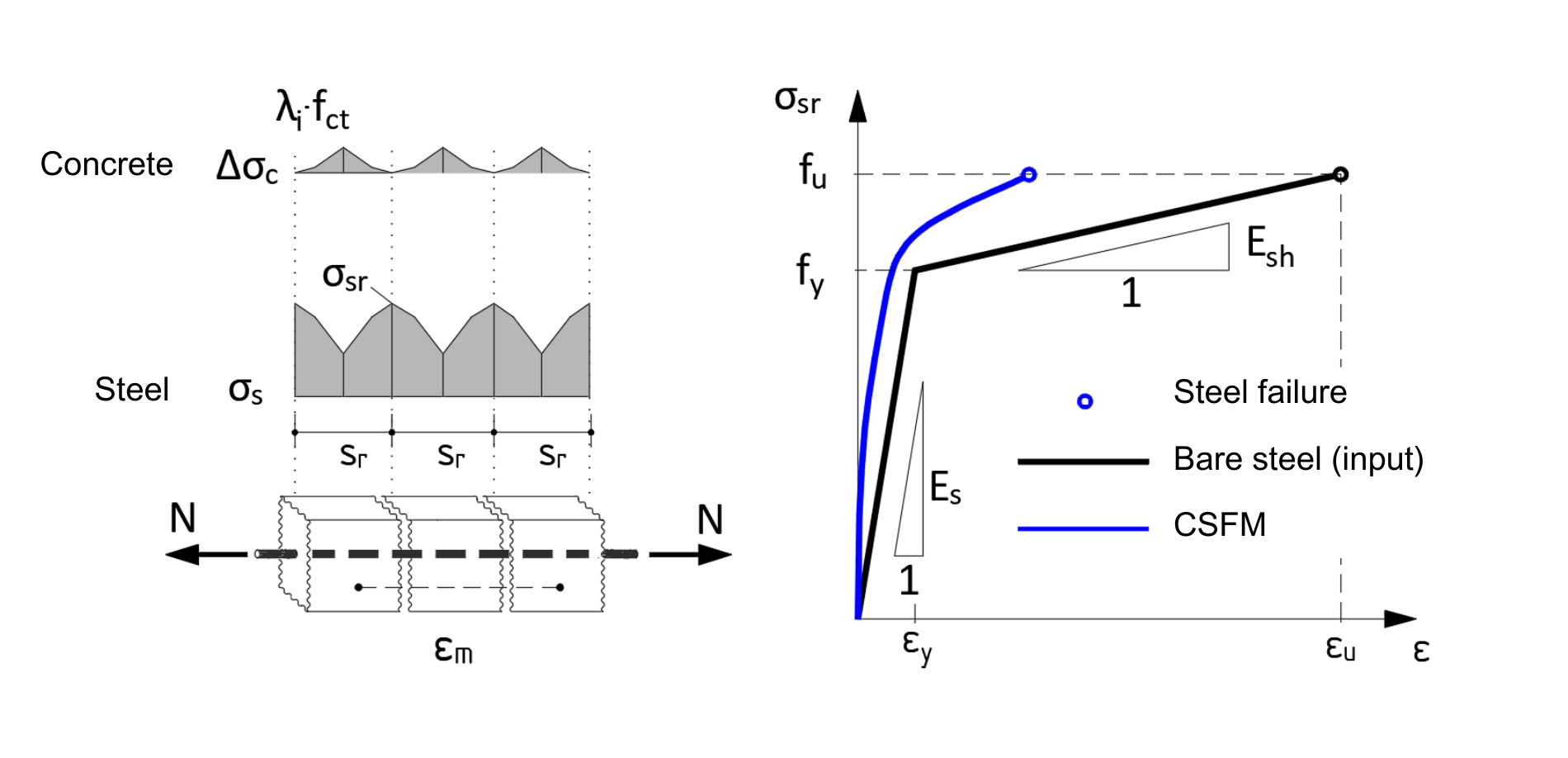
Abb. 6 Prinzip der Zugaussteifung
Weiterhin berücksichtigt das CSFM die Mitwirkung des Betons zwischen den Rissen (Tension Stiffening) auf die Bewehrung. Im Berechnungsmodell wird der mittlere Bewehrungsgrad εm verwendet. Dann wird das Spannungs-Dehnungs-Diagramm der Bewehrung modifiziert (Abb. 6). Dies ermöglicht eine realistische Darstellung der Steifigkeit einer durch Risse geschädigten Stahlbetonkonstruktion. Es gilt jedoch weiterhin, dass die Zugfestigkeit des Betons nicht zur Tragfähigkeit beiträgt. Die maximale Spannung in der Bewehrung σsr in den Rissen ist für die Bemessung entscheidend (Abb. 6).
CSFM verwendet gängige einachsige Materialmodelle (Spannungs-Dehnungs-Diagramme), die in Bemessungsnormen definiert sind. Der Standardansatz, die Methode der Teilsicherheitsbeiwerte, wird dann zur Bewertung des GZT verwendet. Die Einfachheit der Methode macht sie für die technische Praxis geeignet und steht im Einklang mit den Bemessungsnormen.
Obwohl es sich um eine nichtlineare FEA-Analyse handelt, muss der Tragwerksplaner keine zusätzlichen Materialeigenschaften und Betoneigenschaften in die Berechnung eingeben, die möglicherweise in der Entwurfsphase noch gar nicht zur Verfügung stehen und die notwendig sind, z. B. FEA-Analysen, die nichtlinear sind und auf Bruchmechanik basieren. Wie bereits angedeutet, besteht ein großer Vorteil der CSFM-Analyse neben den Grenzzuständen der Tragfähigkeit in der Möglichkeit, die Grenzzustände der Gebrauchstauglichkeit zu bewerten: Durchbiegungen, Spannungsbegrenzungen und insbesondere die Rissbreite.
Abb. 7 Beispiel für die Darstellung eines Finite-Elemente-Modells in IDEA StatiCa Detail
(Abb. 7) Das FEM-Modell in CSFM setzt sich aus mehreren Arten von finiten Elementen zusammen:
- 1-D Element mit axialer Steifigkeit für die Bewehrung
- 2-D isoparametrisches Element für den Beton
- Endfedern für das Verankerungsmodell der Bewehrung mit Endbehandlung
- Spezielles 2-D-Element zur Modellierung der Kohäsion zwischen Bewehrung und Beton
- Starre und interpolierende Kopplungselemente (Multi-Point Constraints, MPC) zwischen Betonstahl und Beton
Es hat sich gezeigt, dass die CSFM trotz der Einfachheit der Formulierung sehr gute Vorhersagen über das Verhalten und die Tragfähigkeit des Bauteils liefert. Mit anderen Worten, die Methode eignet sich beispielsweise nicht für die Bemessung von Trägern ohne Querkraftbewehrung, die ein potenziell sprödes Verhalten aufweisen. Überprüfungen der Methode, einschließlich Experimenten, finden sich in [1]. Eine detailliertere Beschreibung der Methode ist auch im Abschnitt Theoretischer Hintergrund zu finden.
Es ist klar, dass die Prinzipien der CSFM-Methode allgemein sind und ihre Anwendung daher nicht auf D-Regionen beschränkt ist, sondern für die Modellierung ganzer Bauteile, z. B. Fertigteilträger, verwendet werden kann, und wo das Element zu einem ebenen 2D-Modell vereinfacht werden kann. Die Methode und ihre Umsetzung in Software (IDEA StatiCa Detail) wurden auch um die Möglichkeit erweitert, vorgespannte und nachgespannte Bewehrung zu spezifizieren.
3. Beispiel für den Entwurf einer Pfeilerkappe
Die praktische Anwendung von CSFM wird anhand des Entwurfs des Brückenpfeilers in Abbildung 8 gezeigt. Es handelt sich um den zweiten Pfeiler einer durchgehenden Brücke mit drei Spannweiten von 30,0 m, 42,0 m und 30,0 m. Die Betongüte in C40/50 und die Dicke (in Brückenlängsrichtung) beträgt 2,0 m.
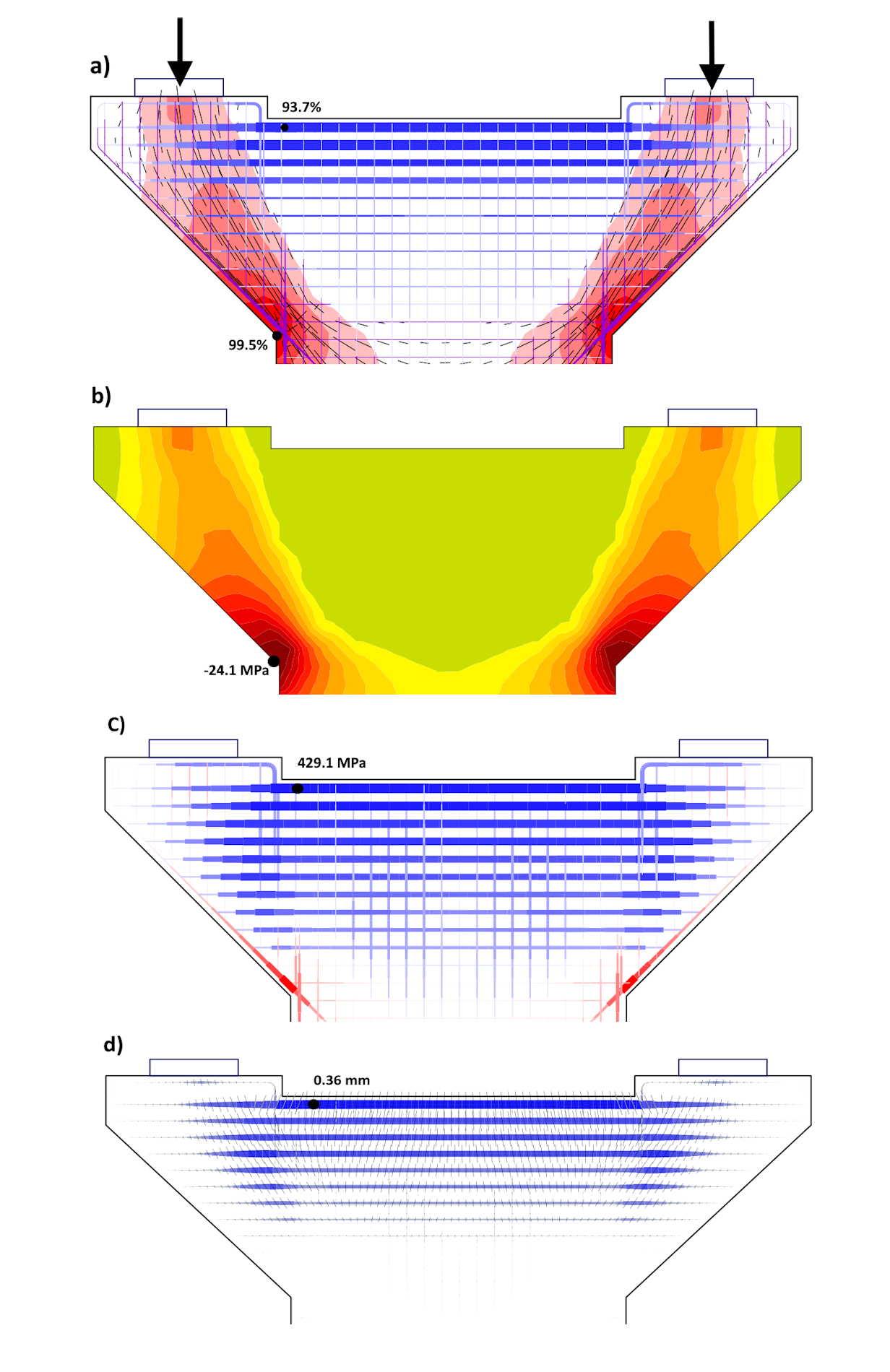
Abb. 8 Pfeilerkopf: a) Zusammenfassender Entwurf; b) Druckspannung im Beton in GZT; c) Zugspannung in der Bewehrung in GZT; d) Rissbreite in GZG
Am oberen Ende des Pfeilers wurde zunächst ein Querträger aus B500-Bewehrung 20xϕ28+20xϕ25 - die oberen vier Lagen - bemessen. Bild 8a zeigt eine zusammenfassende Bemessung im Grenzzustand der Tragfähigkeit, in der die Druckspannungen im Beton, die Richtungen der Druckspannungen und die Spannungen in der Bewehrung angegeben sind. Die detailliertere Spannungsverteilung im Beton und in der Bewehrung ist dann in den Bildern 8b und 8c dokumentiert. Die Querbewehrung liegt knapp unterhalb der Streckgrenze, auch die Spannungen im Beton (und die relativen Dehnungen) sind bei GZT zufriedenstellend. Das Ergebnis der Rissbreitenberechnung (Abb. 8d) zeigt jedoch, dass die Bemessung in GZG nicht erfüllt ist: wmax = 0,36 mm > wlim = 0,3 mm. Um die Grenzrissbreite einzuhalten, ist es notwendig, die Bewehrung des Querträgers auf 20xϕ32+20xϕ28 zu erhöhen. Im Fall von wlim = 0,2 mm müsste die Bewehrung des Querträgers sogar auf 24xϕ32+24xϕ28 erhöht werden.
Schlussfolgerung
CSFM eignet sich für die Ingenieurpraxis, weil es einfache Materialmodelle verwendet, die in einer Bemessungsnorm definiert sind. Neben den Grenzzuständen der Tragfähigkeit ermöglicht es auch die Bemessung von Grenzzuständen der Gebrauchstauglichkeit. Für diese war die Bewertung mit Hilfe von Fachwerkmodellen bisher nur schwer vorstellbar. Durch die Implementierung der Methode in IDAStatiCa Detail ist es dann möglich, das Tragwerksverhalten realistisch zu erfassen und Diskontinuitätsbereiche effizient und sicher zu bemessen.
Entwickelt wurde das CSFM vor allem durch die Arbeit von Professor Walter Kaufmann, Leiter der Professur für Tragwerksplanung an der Eidgenössischen Technischen Hochschule (ETH) Zürich. Er und sein Team haben die Methode und ihre Softwareimplementierung auch verifiziert.
Literatur
[1] KAUFMANN, Walter, et al: Verträgliche Spannungsfeldbemessung von Konstruktionsbeton, ETH Zürich, 2020, ISBN 978-3-906916-95-8,
[2] KAUFMANN, W., MARTI, P.: Structural Concrete: Cracked Membrane Model. Zeitschrift für Hochbau 124 (12): 1467-75, 1998 https://doi.org/10.1061/(ASCE)0733-9445(1998)124:12(1467)
[3] KRAUS, M., M. WEBER, W. KAUFMANN, W, BOBEK, L.: Numerische Analyse von experimentell geprüften Rahmenecken mit Öffnungsmomenten mittels der Compatible Stress Field Method (CSFM). In: Computational Modelling of Concrete and Concrete Structures, S. 694-03. CRC Press, 2022 https://doi.org/10.1201/9781003316404
Autor
Ing. Pavel Kaláb, Ph.D.
IDEA StatiCa s.r.o.