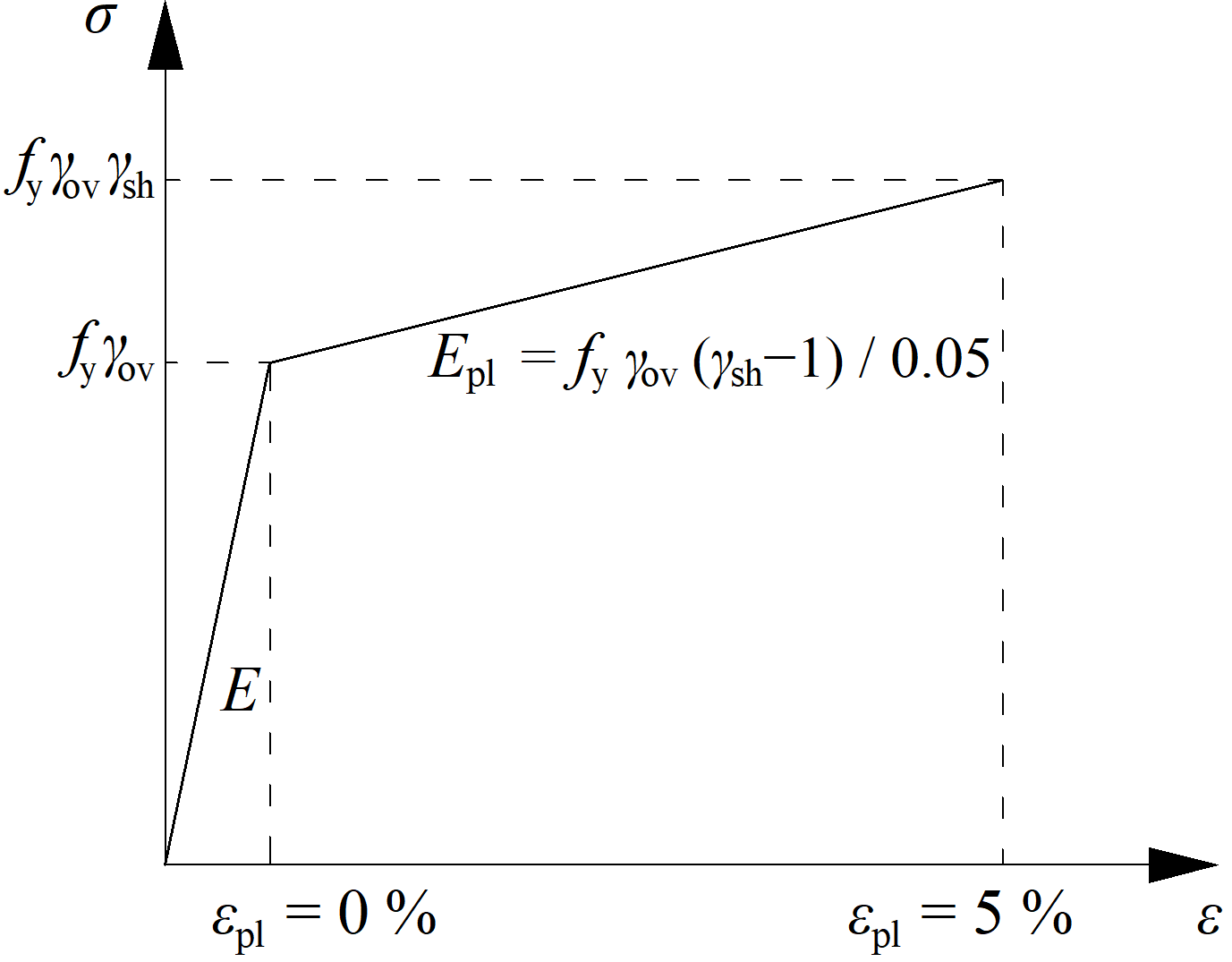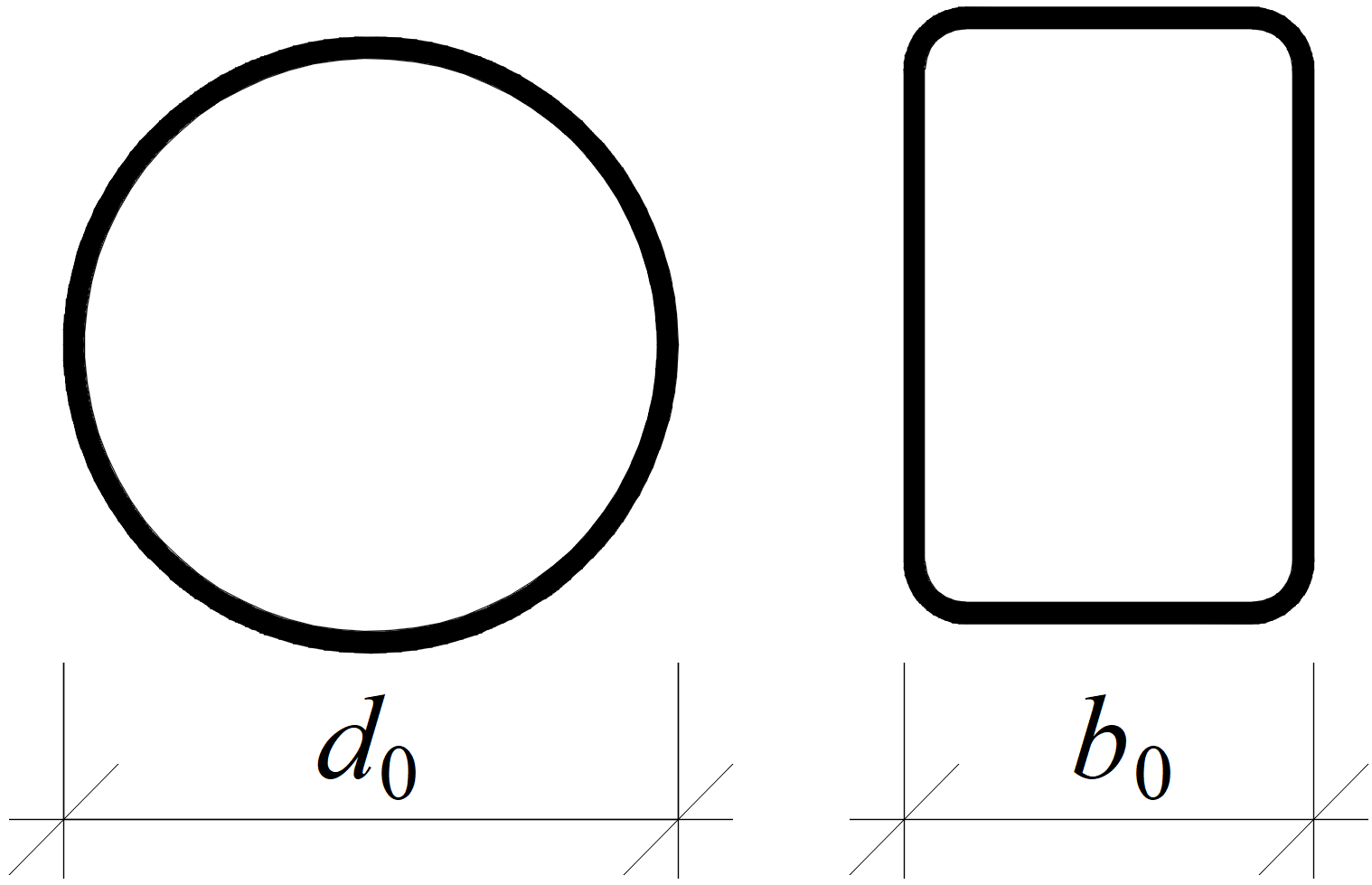Staafelementen hebben de voorkeur van ingenieurs bij het ontwerpen van staalconstructies. Er zijn echter veel locaties op de constructie waar de elemententheorie niet geldig is, bijvoorbeeld lasverbindingen, boutverbindingen, funderingen, gaten in muren, de taps toelopende hoogte van de doorsnede en puntbelastingen. De constructieberekeningen op zulke plaatsen zijn moeilijk en vereisen speciale aandacht. Het gedrag is niet-lineair en de niet-lineariteiten moeten worden gerespecteerd, bijv. het vloeien van het materiaal van platen, contact tussen kopplaten of voetplaat en betonpoer, eenzijdige acties van bouten en ankers, lassen. Ontwerpnormen, bijv. EN1993-1-8, en ook technische literatuur bieden technische oplossingsmethoden. Hun algemene kenmerk is afleiding voor typische constructievormen en eenvoudige belastingen. De componentenmethode wordt heel vaak gebruikt.

Componentenmethode

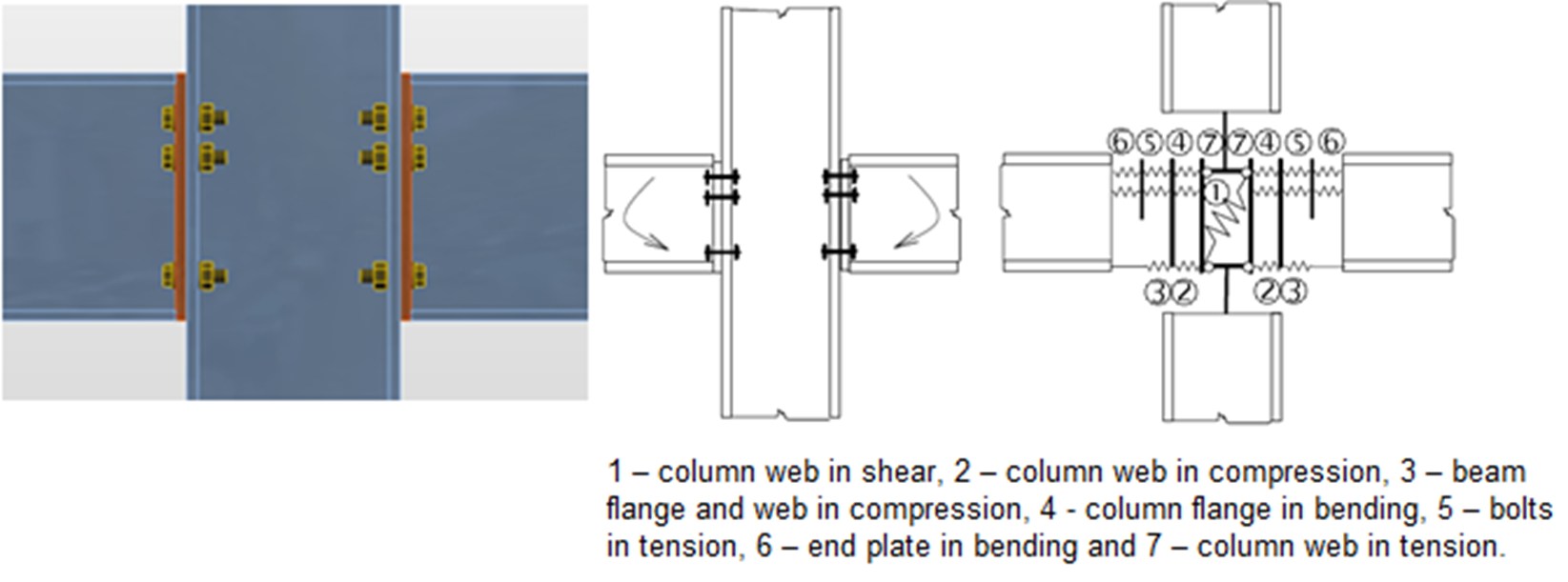
De componentenmethode (CM) lost de verbinding op als een systeem van onderling verbonden onderdelen - componenten. Per verbindingstype wordt het bijbehorende model gebouwd om krachten en spanningen in elke component te kunnen bepalen - zie de volgende afbeelding.

De componenten van een verbinding met geboute kopplaten gemodelleerd door veren

Elke component wordt afzonderlijk gecontroleerd met behulp van overeenkomstige formules. Omdat er voor elk verbindingstype het juiste model moet worden gemaakt, heeft het gebruik van de methode beperkingen bij het oplossen van verbindingen met algemene vormen en algemene belastingen.

IDEA StatiCa heeft samen met een projectteam van de afdeling Staal- en Houtconstructies van de Faculteit Civiele Techniek in Praag en het Instituut voor Metaal- en Houtconstructies van de Faculteit Civiele Techniek van de Technische Universiteit van Brno een methode ontwikkeld voor geavanceerd ontwerp van staalverbindingen.

Component Based Finite Element Model (CBFEM) methode is:

Algemeen genoeg om bruikbaar te zijn voor de meeste verbindingen, funderingen en details in de ingenieurspraktijk.
Eenvoudig en snel genoeg in de dagelijkse praktijk om resultaten te leveren in een tijd die vergelijkbaar is met de huidige methoden en hulpmiddelen.
Uitgebreid genoeg om constructeurs duidelijke informatie te geven over het gedrag van verbindingen, spanning, rek en reserves van individuele componenten en over de algemene veiligheid en betrouwbaarheid.

De CBFEM-methode is gebaseerd op het idee dat de meeste geverifieerde en zeer bruikbare onderdelen van CM behouden moeten blijven. Het zwakke punt van CM - de algemeenheid bij het analyseren van spanningen van individuele componenten - werd vervangen door modellering en analyse met behulp van de Finite Element Method (FEM).

FEM is een algemene methode die vaak wordt gebruikt voor constructieberekeningen. Het gebruik van FEM voor het modelleren van verbindingen van elke vorm lijkt ideaal (Virdi, 1999). De elastisch-plastische analyse is vereist omdat het staal gewoonlijk meegeeft in de constructie. In feite zijn de resultaten van de lineaire berekening nutteloos voor het ontwerp van de verbinding.

FEM-modellen worden gebruikt voor onderzoek naar het gedrag van verbindingen waarbij meestal ruimtelijke elementen en gemeten waarden van materiaaleigenschappen worden toegepast.

FEM-model van een verbinding voor onderzoek. Het gebruikt ruimtelijke 3D-elementen voor zowel platen als bouten.

Zowel de lijven als de flenzen van verbonden elementen worden gemodelleerd met behulp van schaalelementen in het CBFEM-model waarvoor de bekende en geverifieerde oplossing beschikbaar is.

De bevestigingsmiddelen - bouten en lassen - zijn het moeilijkst vanuit het oogpunt van het rekenmodel. Het modelleren van dergelijke elementen in algemene FEM-programma's is moeilijk omdat de programma's niet de vereiste eigenschappen bieden. Er moesten dus speciale FEM-componenten worden ontwikkeld om het gedrag van lassen en bouten in een verbinding te modelleren.

CBFEM geboute verbinding in IDEA StatiCa

CBFEM-model van boutverbinding met kopplaten

Knopen van elementen worden gemodelleerd als massaloze punten bij het analyseren van een stalen frame of liggerconstructie. Evenwichtsvergelijkingen worden samengesteld in verbindingen en snedekrachten op de uiteinden van liggers worden bepaald na het oplossen van de hele constructie. In feite wordt de knoop belast door deze krachten. De resultante van krachten van alle elementen in de knoop is nul - de hele verbinding is in evenwicht.

De echte vorm van een verbinding is niet bekend in het constructiemodel. De ingenieur bepaalt alleen of de verbinding verondersteld wordt stijf of scharnierend te zijn.

Het is noodzakelijk om een betrouwbaar model van de verbinding te maken dat de werkelijke toestand respecteert, om de verbinding goed te kunnen ontwerpen. De uiteinden van elementen met een lengte van een 2-3 veelvoud van de maximale doorsnedehoogte worden gebruikt in de CBFEM-methode. Deze segmenten worden gemodelleerd met behulp van schaalelementen.

Een theoretische (massaloze) knoop en de echte vorm van de verbinding zonder gewijzigde uiteinden van het element

Voor een betere nauwkeurigheid van het CBFEM-model worden de eindkrachten op 1D-elementen toegepast als belastingen op de uiteinden van segmenten. Zesling van krachten van de theoretische verbinding worden overgebracht naar het einde van het segment - de waarden van de krachten blijven behouden, maar de momenten worden gewijzigd door de acties van krachten op overeenkomstige armen.

De uiteinden van segmenten bij de knoop zijn niet verbonden. De verbinding moet gemodelleerd worden. In de CBFEM-methode worden zogenaamde fabricagebewerkingen gebruikt om de verbinding te modelleren. Fabricagebewerkingen zijn met name: sneden, offsets, gaten, verstijvers, ribben, kop- en koppelplaten, hoekstalen, schetsplaten en andere. Bevestigingselementen (lassen en bouten) worden ook toegevoegd.

IDEA StatiCa Connection kan twee soorten berekeningen uitvoeren:

Geometrisch lineaire berekening met materiaal- en contactnonlineariteiten voor spanning-rek analyse,
Eigenwaardeanalyse om de mogelijkheid van knik te bepalen.

Bij verbindingen is de geometrisch niet-lineaire berekening niet nodig, tenzij de platen erg slank zijn. Plaatslankheid kan worden bepaald door knikberekening. Zie hoofdstuk 3.9 voor de limietslankheid waarbij een geometrisch lineaire berekening nog steeds voldoende is. De geometrisch niet-lineaire berekening is niet geïmplementeerd in de software.

Wil je je vaardigheden verbeteren? Bezoek onze campus

Leer hoe je IDEA StatiCa effectief gebruikt met onze e-learningcursussen die je zelf kunt volgen

Begin met leren

Materiaal model

De meest voorkomende materiaaldiagrammen die worden gebruikt bij het modelleren van eindige elementen van constructiestaal zijn het ideale plastisch of elastisch model met een bijbehorend spanning-rek diagram. Het werkelijke spanning-rek diagram wordt berekend uit de materiaaleigenschappen van staal bij een omgevingstemperatuur verkregen in trektests. De werkelijke spanning en rek kunnen als volgt worden verkregen:

\[ \sigma_{true}=\sigma (1 + \epsilon) \]

\[ \epsilon_{true}=\ln (1 + \epsilon) \]

waar σ_true is true stress, ε_true true strain, σ engineering spanning, and ε engineering rek.

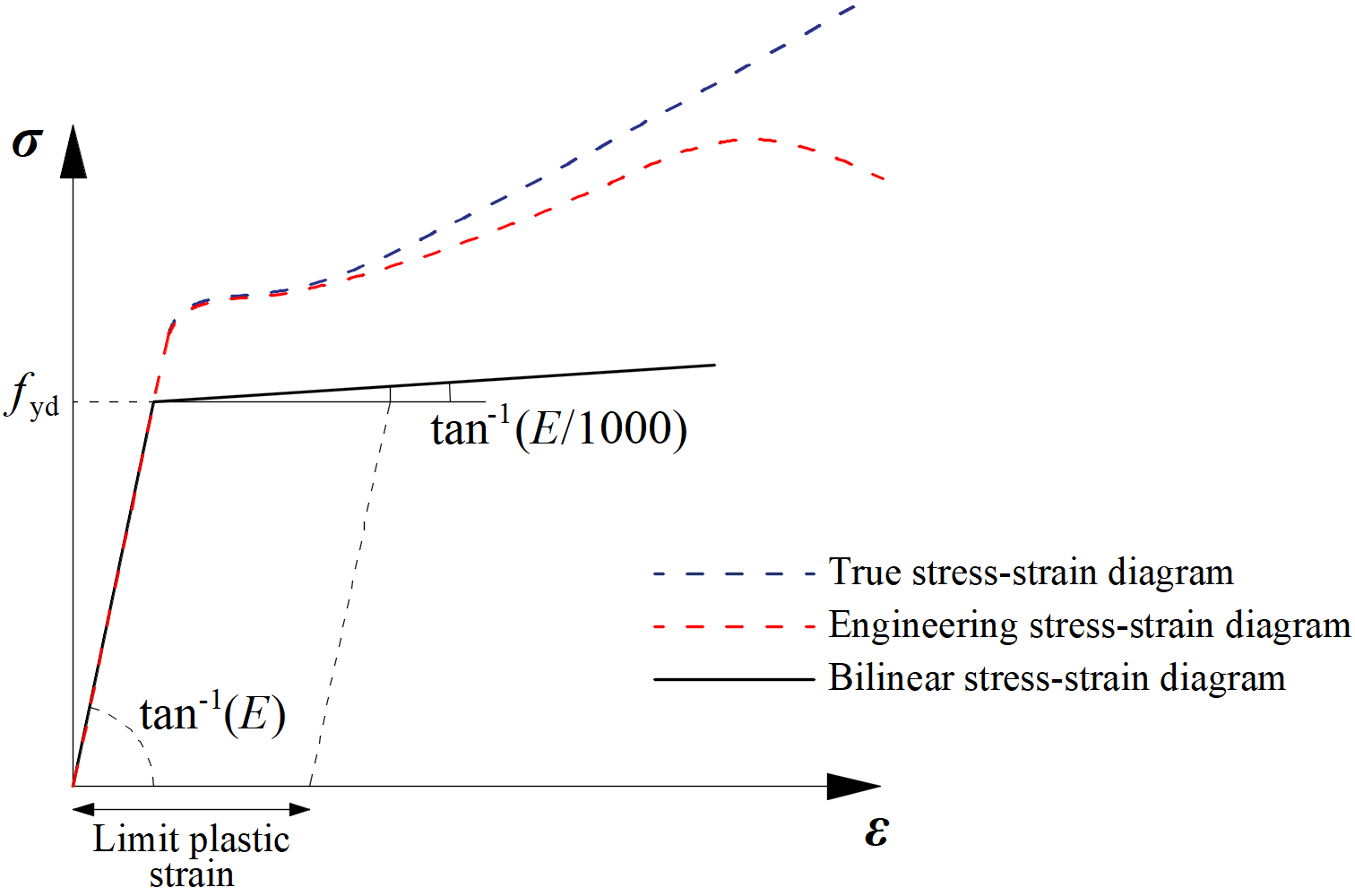
De platen in IDEA StatiCa Connection zijn gemodelleerd met elastisch-plastisch materiaal volgens

EN1993-1-5, Par. C.6, (2), tan^-1 (E/1000). Het materiaalgedrag is gebaseerd op het von Mises vloeicriterium. Aangenomen wordt dat het elastisch is voordat de ontwerpvloeigrens wordt bereikt, f_yd.

Het uiterste grenstoestand criterium voor gebieden die niet vatbaar zijn voor knik, is het bereiken van de grenswaarde van de rek. De waarde van 5% wordt aanbevolen ( EN1993-1-5, App. C, Par. C.8, Note 1).

spannings-rek diagram van materiaal model in CBFEM IDEA CONNECTION

Materiaal diagram of steel in numerical models

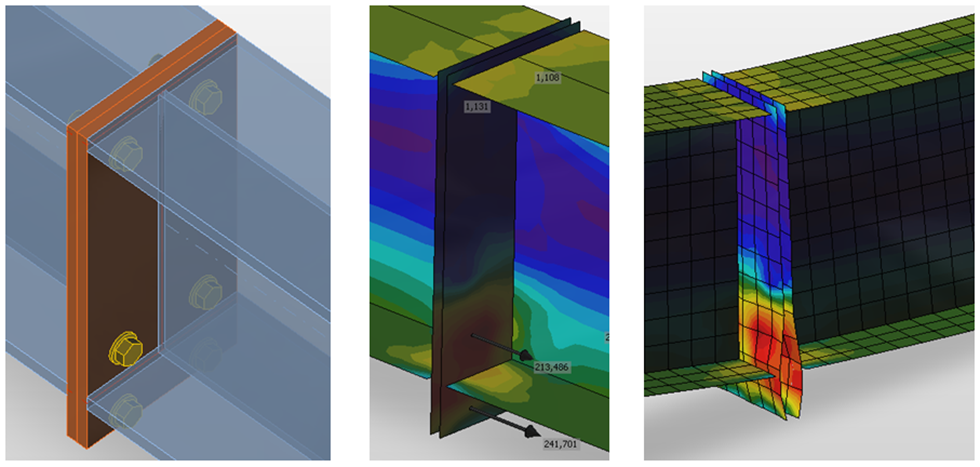
De grenswaarde van plastische rek wordt vaak besproken. In feite heeft de uiteindelijke belasting een lage gevoeligheid voor de grenswaarde van plastische rek wanneer het ideale plastisch model wordt gebruikt. Het wordt gedemonstreerd in het volgende voorbeeld van een ligger-kolomverbinding. Een IPE 180 is verbonden met HEB 300 en belast door een buigend moment. De invloed van de grenswaarde van plastische rek op de weerstand van de balk wordt weergegeven in de volgende afbeelding. De limiet plastische rek verandert van 2% naar 8%, maar de verandering in momentweerstand is minder dan 4%.

knoopbelasting, spanningsweergave in platen en rekweergave in IDEA CONNECTION

Een voorbeeld van voorspelling de UGT van een ligger-kolom verbinding in staal

Plastiche rek weerstand van de verbinding in IDEA CONNECTION

De invloed van de limiet waarde van plastische rek op het momentweerstand

Plaatmodel en netconvergentie

Een toename van het aantal elementen levert nauwkeurigere resultaten op, maar dat gaat ten koste van de rekenkracht.

Plaatmodel

Shell-elementen worden aanbevolen voor het modelleren van platen in de FEA van structurele verbindingen. Er worden vierhoekige shell-elementen met 4 knopen en knopen op de hoeken toegepast. Zes vrijheidsgraden worden beschouwd in elk knoop: 3 verplaatsingen (u_x, u_y, u_z) en 3 rotaties (φ_x, φ_y, φ_z). Vervormingen van het element worden verdeeld in de membraan- en de buigcomponenten.

De formulering van het membraangedrag is gebaseerd op het werk van Ibrahimbegovic (1990). Rotaties loodrecht op het vlak van het element worden in rekening gebracht. Er wordt een volledige 3D-formulering van het element gegeven. In de formulering van het buiggedrag van een element op basis van de Mindlin-hypothese wordt rekening gehouden met afschuivingsvervormingen uit-het-vlak. Onze eigen gestabiliseerde variant van Mindlin vierplaatelement met constant afschuifvervorming langs de rand wordt toegepast. De elementen zijn geïnspireerd door MITC4-elementen; zie Dvorkin (1984). De shell wordt verdeeld in vijf integratielagen door de dikte van de plaat in elk integratiepunt en het plastisch gedrag wordt in elk punt geanalyseerd. Dit wordt Gauss-Lobatto integratie genoemd. De niet-lineaire elastisch-plastische fase van het materiaal wordt in elke laag geanalyseerd op basis van de bekende spanningen. Er worden alleen de maximale spanningen en vervormingen van alle lagen getoond.

Netconvergentie

Er bestaan enkele criteria voor het genereren van de mesh in het verbindingsmodel. De verbindingscontrole moet onafhankelijk zijn van de elementgrootte. Netgeneratie op een afzonderlijke plaat is probleemloos. Er moet aandacht besteed worden aan complexe geometrieën zoals verstijfde panelen, T-stuiken en voetplaten. Voor gecompliceerde geometrieën moet de gevoeligheidsanalyse met betrekking tot net-discretisatie worden uitgevoerd.

Alle platen van een liggerdoorsnede hebben een gemeenschappelijke opdeling in elementen. De grootte van de gegenereerde eindige elementen is beperkt. De minimale elementgrootte is ingesteld op 10 mm en de maximale elementgrootte op 50 mm (kan worden ingesteld in Norminstelling). Netten op flenzen en lijven zijn onafhankelijk van elkaar. Het standaard aantal eindige elementen is ingesteld op 8 elementen per doorsnedehoogte zoals weergegeven in de volgende figuur. De gebruiker kan de standaardwaarden wijzigen in Norminstelling.

De mesh op een ligger met beperkingen tussen het lijf en de flensplaat

De mesh van de kopplaten is afzonderlijk en onafhankelijk van andere verbindingsdelen. De standaard eindige-elementengrootte is ingesteld op 16 elementen per doorsnedehoogte zoals weergegeven in de figuur.

De mesh op een kopplaat met 7 elementen langs de breedte

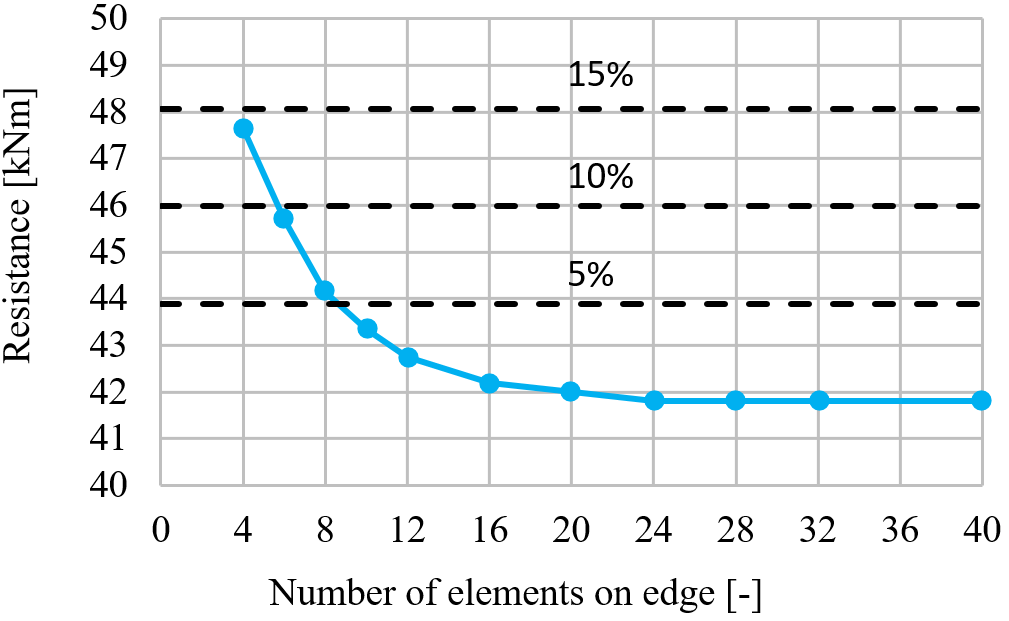
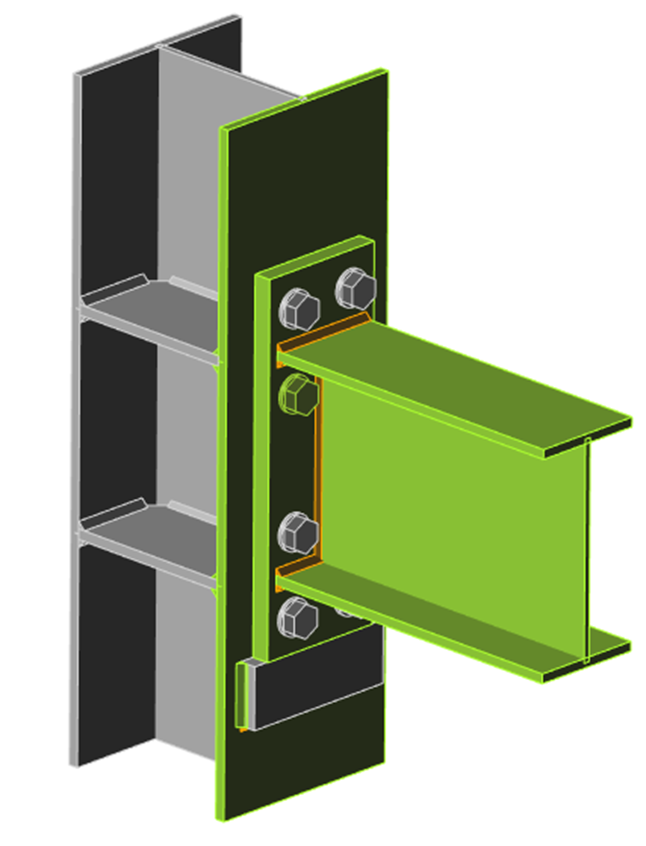
Het volgende voorbeeld van een verbinding tussen ligger en kolom toont de invloed van de netwijdte op de momentweerstand. Een open doorsnede ligger IPE 220 is verbonden met een open doorsnede kolom HEA 200 en belast met een buigmoment zoals weergegeven in de volgende figuur. De kritische component is het kolompaneel in afschuiving. Het aantal eindige elementen langs de doorsnedehoogte varieert van 4 tot 40 en de resultaten worden vergeleken. Stippellijnen geven de 5%, 10% en 15% verschillen weer. Het wordt aanbevolen om de doorsnedehoogte onder te verdelen in 8 elementen.

Een balk-kolom verbindingsmodel en plastische vervormingen bij uiterste grenstoestand

De invloed van het aantal elementen op de momentweerstand

Er wordt een gevoeligheidsstudie van de mesh van een slanke samengedrukte verstijver van een kolom lijfpaneel gepresenteerd. Het aantal elementen langs de breedte van de verstijver varieert van 4 tot 20. De eerste knikmodus en de invloed van een aantal elementen op de knikweerstand en de kritische belasting worden weergegeven in de volgende figuur. Er wordt het verschil van 5% en 10% weergegeven. Het wordt aanbevolen om 8 elementen langs de verstijversbreedte te gebruiken.

De eerste knikmodus en de invloed van het aantal elementen langs de verstijver op de momentweerstand

Er wordt een meshgevoeligheidsstudie van een T-stuik op trek voorgesteld. De helft van de flensbreedte is onderverdeeld in 8 tot 40 elementen en de minimale elementgrootte is ingesteld op 1 mm. De invloed van het aantal elementen op de weerstand van de T-stuik wordt getoond in de volgende figuur. De stippellijnen geven het verschil van 5%, 10% en 15% weer. Het wordt aanbevolen om 16 elementen te gebruiken op de helft van de flensbreedte.

De invloed van het aantal elementen op de T-stuikweerstand

Contacten tussen stalen verbindingsplaten

De standaard penaltymethode wordt aanbevolen voor het modelleren van contact tussen platen. Wanneer er een doordringing van een knoop in een tegenoverliggend contactoppervlak wordt gedetecteerd, wordt er penaltystijfheid toegevoegd tussen de knoop en de tegenoverliggende plaat. De penaltystijfheid wordt gecontroleerd door een heuristisch algoritme tijdens de niet-lineaire iteratie om een betere convergentie te krijgen. De oplosser detecteert automatisch het doordringingspunt en lost de contactkrachtverdeling op tussen de doorgedrongen knoop en knopen op de tegenoverliggende plaat. Dat maakt het mogelijk om contact te maken tussen verschillende netten. Het voordeel van de penaltymethode is de automatische opbouw van het model. Het contact tussen de platen heeft een grote invloed op de herverdeling van krachten in de verbinding.

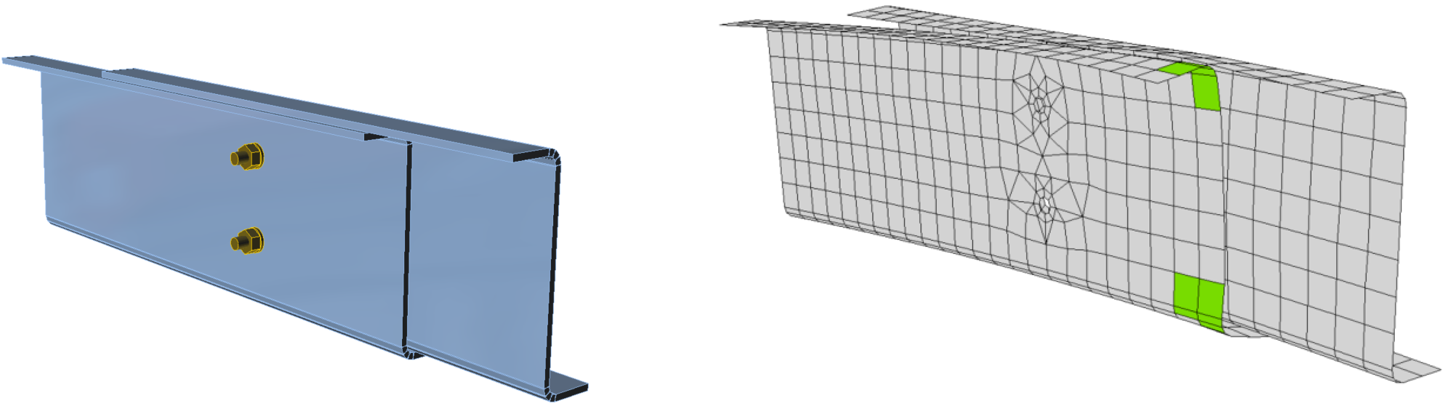
Een voorbeeld van het scheiden van platen in contact tussen het lijf en de flenzen van twee overlappende gordingen met Z-profielen

Het is mogelijk om contact toe te voegen tussen

twee oppervlakken,
twee randen,
rand en oppervlak.

Een voorbeeld van rand-op-rand contact tussen de zitting en de kopplaat

Een voorbeeld van contact van rand-op-oppervlak tussen de onderste flens van de ligger en de kolomflens

De spanningen in contacten kunnen gevisualiseerd worden en de waarden worden weergegeven in de controletabel van platen. De contactspanningen zijn echter alleen informatief en worden in geen enkele controle gebruikt. Ook wordt er geen rekening gehouden met de spanning door de dikte van schaalelementen.

Lassen

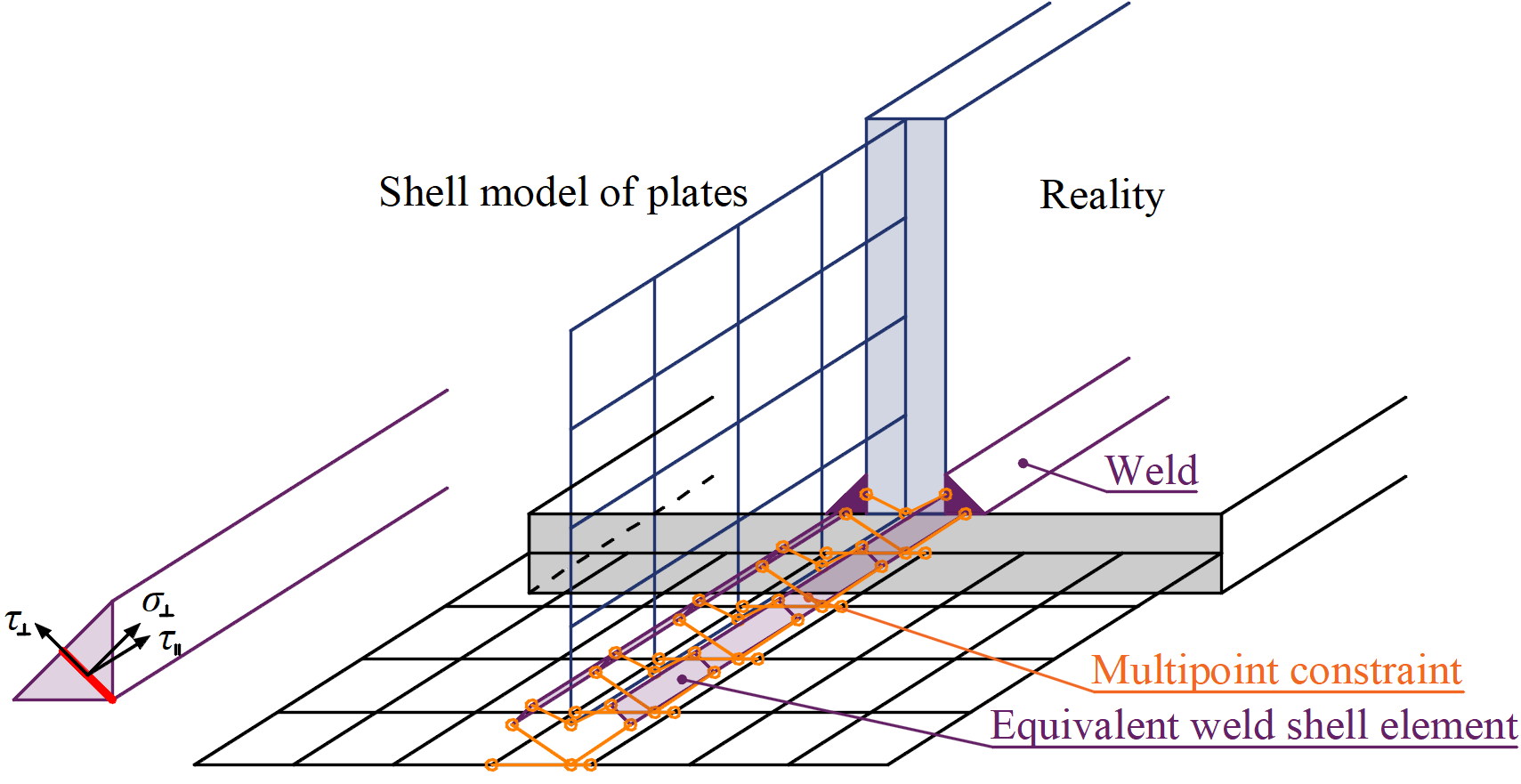
Er bestaan verschillende opties om lassen te benaderen in numerieke modellen. De grote vervormingen maken de mechanische analyse complexer en het is mogelijk om verschillende mesh-beschrijvingen, verschillende kinetische en kinematische variabelen en constitutieve modellen te gebruiken. Over het algemeen worden de verschillende soorten geometrische 2D- en 3D-modellen en daarmee eindige elementen met hun toepasbaarheid voor verschillende nauwkeurigheidsniveaus gebruikt. Het meest gebruikte materiaalmodel is het gebruikelijke plasticiteitsmodel op basis van het von Mises-vloeicriterium. Er worden twee benaderingen beschreven die voor lassen worden gebruikt. Restspanning en vervorming veroorzaakt door lassen worden niet verondersteld in het ontwerpmodel.

De belasting wordt overgedragen via kracht-vervormingsbeperkingen op basis van de Lagrangiaanse formulering op de tegenoverliggende plaat. De verbinding wordt multi-point constraint (MPC) genoemd en relateert de eindige-elementknooppunten van de ene plaatrand aan de andere. De eindige elementen knooppunten zijn niet direct verbonden. Het voordeel van deze aanpak is de mogelijkheid om EE_netten met verschillende dichtheden te verbinden. De constraint maakt het mogelijk om het middenlijnoppervlak van de verbonden platen te modelleren met de offset, waarbij de werkelijke lasconfiguratie en lasdikte worden gerespecteerd. De belastingsverdeling in de las wordt afgeleid van de MPC, dus de spanningen worden berekend in het keelgedeelte. Dit is belangrijk voor de spanningsverdeling in de plaat onder de las en voor het modelleren van T-stubs.

Plastische herverdeling van spanningen in lassen

Het model met alleen multi-point constraints houdt geen rekening met de stijfheid van de las en de spanningsverdeling is conservatief. Spanningspieken die verschijnen aan het einde van plaatranden, in hoeken en afrondingen, bepalen de weerstand over de gehele lengte van de las. Om dit effect te elimineren, wordt tussen de platen een speciaal elastoplastisch element toegevoegd. Het element respecteert de dikte, positie en oriëntatie van de lasnaad. Het equivalente laslichaam wordt ingevoegd met de bijbehorende lasafmetingen. De niet-lineaire materiaalanalyse wordt toegepast en het elastoplastische gedrag in een gelijkwaardige lasmassa wordt bepaald. De plasticiteitstoestand wordt geregeld door spanningen in de lasdoorsnede. De spanningspieken worden herverdeeld over het langere deel van de laslengte.

Het elastoplastische model van lassen geeft echte spanningswaarden en het is niet nodig om de spanning te middelen of te interpoleren. Berekende waarden bij het meest belaste laselement worden direct gebruikt voor controles van de las. Op deze manier is het niet nodig om de weerstand van multi-oriented lassen, lassen aan niet-verstijfde flenzen of lange lassen te verminderen.

Lasmodel van Lasdefinitie in van elastoplastich materiaal in IDEA CONNECTION

Constraint tussen laselement en netknooppunten

Algemene lassen kunnen, terwijl ze plastische herverdeling gebruiken, worden ingesteld als continu, gedeeltelijk en onderbroken. Doorlopende lassen zijn over de gehele lengte van de rand, gedeeltelijk stelt de gebruiker in staat om offsets van beide kanten van de rand in te stellen, en onderbroken lassen kunnen bovendien worden ingesteld met een ingestelde lengte en een opening.

Bolts and preloaded bolts connections

Bolts

In the Component-Based Finite Element Method (CBFEM), the bolt with its behavior in tension, shear, and bearing is the component described by the dependent nonlinear springs. Bolt assembly consists of bolt, washer, and nut and is simulated by a nonlinear spring, rigid body elements and gap elements.

Bolt in tension

The bolt in tension is described by spring with its initial axial stiffness, design resistance, initialization of yielding, and deformation capacity. The initial axial stiffness is derived analytically in the guideline VDI2230 and in Agerskov (1976).

\[D_{Lb} =\frac{L_s+0.4d_b}{EA_{ss}}\]

\[A_{pp}=\frac{0.75D_H(L_w-D_H)}{D_{W1}^2-D_{W2}^2}\]

\[A_{P1}=\frac{\pi}{4}(D_H^2-D_{W1}^2)\]

\[A_{P2}=\frac{1}{2}(D_{W2}^2-D_H^2)\tan^{-1}A_{pp}\]

\[A_P=A_{P1}+A_{P2}\]

\[D_{LW}=\frac{L_W}{EA_P}\]

\[k=\frac{1}{D_{LB}+D_{LW}}\]

where:

\(d_b\) – bolt diameter
\(D_H\) – bolt head diameter
\(D_{W1}\) – washer inner diameter
\(D_{W2}\) – washer outer diameter
\(L_W\) – washer thickness
\(L_s\) – bolt grip length
\(A_{ss}\) – bolt gross area
\(E\) – Young's modulus of elasticity

The model corresponds to experimental data; see Gödrich et al. (2014). For the initialization of yielding and deformation capacity, it is assumed that plastic deformation occurs in the threaded part of the bolt shank only.

IDEA StatiCa Connection theoretical background for the structural design of steel connections. Bolts and preloaded bolts, shear resistance, and behavior in tensile-shear interaction. Structural design of welded and bolted connections.

Force-deformation diagram for the bearing of the plate

The force-deformation diagram is constructed using the following equations:

Plastic stiffness:

\[ k_t = c_1 k \]

Force at the elastic limit:

\[ F_{t,el} = \frac{F_{t,Rd}}{c_1 c_2 - c_1 +1} \]

Deformation at elastic limit:

\[ u_{el} = \frac{ F_{t,el} }{k} \]

Deformation at plastic limit:

\[ u_{t,Rd} = c_2 u_{el} \]

\[ c_1 = \frac{f_{ub} - f_{yb}}{\frac{1}{4} A E - f_{yb}} \]

\[ c_2 = \frac{AE}{4 f_{yb}} \]

where:

\(F_{t,Rd}\) – bolt design resistance in tension
\(f_{yb}\) – bolt yield strength
\(f_{ub}\) – bolt ultimate strength
\(A\) – elongation after fracture

Bolt in shear

Only the compression force is transferred from the bolt shank to the plate in the bolt hole. It is modeled by interpolation links between the shank nodes and holes edge nodes. The deformation stiffness of the shell element modeling the plates distributes the forces between the bolts and simulates the adequate bearing of the plate.

Bolt holes are considered as standard (default) or slotted (can be set in plate editor). Bolts in standard holes can transfer shear force in all directions, bolts in slotted holes have one direction excluded and can move in this selected direction freely.

The initial stiffness and the design resistance of a bolt in shear is defined by following formulas:

\[k_{el}=\frac{1}{\frac{1}{k_{11}}+\frac{1}{k_{12}}}\]

\[k_{11} = \frac{8d_b^2f_{ub}}{d_{M16}}\]

\[k_{12}=12k_td_bf_{up}\]

\[k_t=\min \left ( 2.5,\, \frac{1.5t_{min}}{d_{M16}} \right ) \]

\[k_{pl}=\frac{k_{el}}{1000}\]

where:

\(d_b\) – bolt diameter
\(f_{ub}\) – bolt ultimate strength
\(d_{M16}=16 \textrm{ mm}\) – diameter of the reference bolt M16
\(f_{up}\) – ultimate strength of the connected plate
\(t_{min}\) – minimum thickness of the connected plate

The spring representing the bolt in shear has bi-linear force deformation behavior. Initialization of yielding is expected at:

\[F_{V,el}=0.999 F_{V,Rd}\]

Deformation capacity is considered as:

\[\delta_{pl}=\delta_{el}\]

where:

\(F_{V,el}\) – bolt in shear elastic resistance
\(F_{V,Rd}\) – bolt in shear resistance
\(\delta_{el}\) – bolt in shear elastic deformation

Interaction between tension and shear

Interaction of the axial and the shear force can be introduced directly in the analysis model. The distribution of forces reflects the reality better (see enclosed diagram). Bolts with a high tensile force take less shear force and vice versa.

Example of the interaction of axial and shear force (EC)

Preloaded bolts

Preloaded bolts are used in cases when minimization of deformation is needed. The tension model of a bolt is the same as for standard bolts. The shear force is not transferred via bearing but via friction between gripped plates.

The design slip resistance of a preloaded bolt is affected by an applied tensile force.

IDEA StatiCa Connection checks the pre-slipping limit state of preloaded bolts. If there is a slipping effect, bolts do not satisfy the check. Then the post-slipping limit state should be checked as a standard bearing check of bolts where bolt holes are loaded in bearing and bolts in shear.

The user can decide which limit state will be checked. Either it is resistance to major slip or post-slipping state in shear of bolts. Both checks on one bolt are not combined in one solution. It is assumed that the bolt has a standard behavior after a major slip and can be checked by the standard bearing procedure.

The moment load of connection has a small influence on the shear capacity. Nevertheless, a friction check on each bolt simply is solved separately. This check is implemented in FEM component of the bolt. There is no information in a general way on whether the external tension load of each bolt is from the bending moment or from the tension load of the connection.

Stress distribution in standard shear bolt connection

Stress distribution in slip-resistant shear bolt connection

Ankerbouten

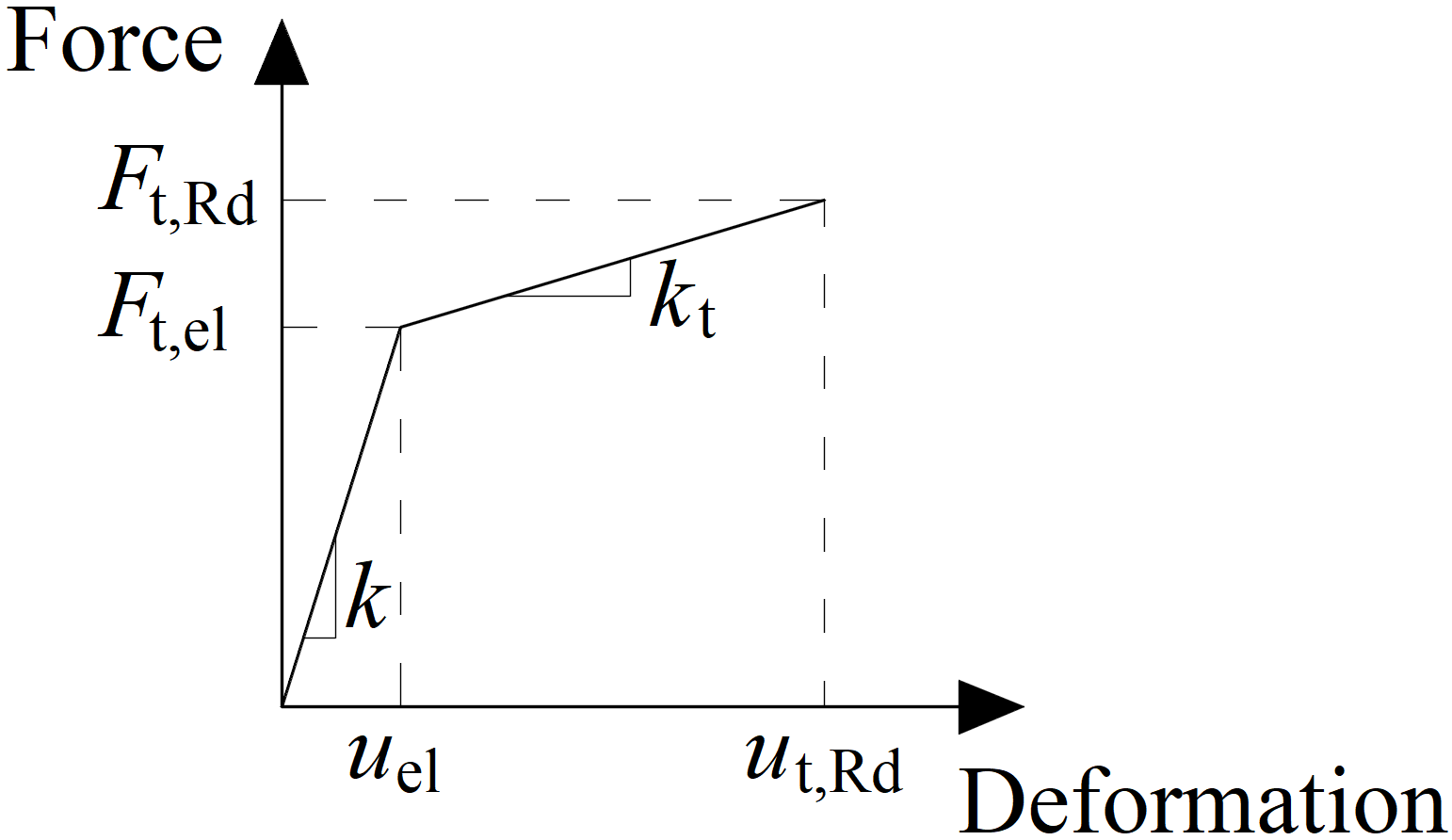
De ankerbout wordt gemodelleerd volgens dezelfde procedures als constructiebouten. De bout is bevestigd aan één zijde van het betonblok. De lengte, L_b, die gebruikt wordt voor de berekening van de stijfheid van de bout, wordt genomen als de som van de helft van de dikte van de moer, de dikte van de sluitring, t_w, de dikte van de voetplaat, t_bp, de dikte van de mortel of de spleet, t_g, en de vrije lengte die in het beton is ingebed, die naar verwachting 8d zal bedragen, waarbij d de boutdiameter is. Factor 8 kan worden bewerkt in de Norminstelling. Deze waarde is in overeenstemming met de Componentenmethode (EN1993-1-8); de vrije lengte in het beton kan worden aangepast in de Norminstelling. De stijfheid onder trek wordt berekend als k = E A_s / L_b. Het last-vervorming diagram van de ankerbout is weergegeven in de volgende figuur. De waarden volgens ISO 898:2009 zijn samengevat in de tabel en in de formules hieronder.

Last–vervorming diagram van de ankerbout

\[ F_{t,el}=\frac{F_{t,Rd}}{c_1 c_2 - c_1 + 1} \]

\[ k_t = c_1 k; \qquad c_1 = \frac{R_m - R_e}{\left ( \frac{1}{4} A - \frac{R_e}{E} \right )E} \]

\[ u_{el} = \frac{F_{t,el}}{k}; \qquad u_{t,Rd} = c_2 u_{el}; \qquad c_2 = \frac{AE}{4R_e} \]

waarbij:

A – verlenging
E – Young's elasticiteitsmodulus
F_t,Rd – trekweerstand van ankers
R_m – uiterste (trek)sterkte
R_e – vloeisterkte

De stijfheid van de ankerbout in afschuiving wordt genomen als de stijfheid van de structurele bout in afschuiving.

Ankerbouten met stand-off

Ankers met stand-off kunnen worden gecontroleerd als een constructiefase voordat de kolomvoet wordt gevoegd, of als een permanente toestand. Een anker met stand-off is ontworpen als een staafelement dat wordt belast door dwarskracht, buigmoment en druk- of trekkracht. Het anker is aan beide zijden bevestigd; één zijde bevindt zich 0,5×d onder het betonniveau, de andere zijde bevindt zich in het midden van de plaatdikte. De kniklengte wordt conservatief aangenomen als tweemaal de lengte van het staafelement. Er wordt een plastisch weerstands-moment gebruikt. De krachten in het anker met stand-off worden bepaald met behulp van eindige elementenberekening. Het buigmoment is afhankelijk van de stijfheidsverhouding van ankers en voetplaat.

Ankers met stand-off - bepaling van hefboomarm- en kniklengtes; stijve ankers zijn veilige aanname

Betonblok

Ontwerpmodel

In CBFEM is het handig om de betonblokken te vereenvoudigen als 2D contactelementen. De verbinding tussen het beton en de grondplaat biedt alleen weerstand bij samendrukken. De compressie wordt overgebracht via het Winkler-Pasternak ondergrondmodel dat de vervormingen van het betonblok weergeeft. De trekkracht tussen de grondplaat en het betonblok wordt overgebracht door de ankerbouten. De afschuifkracht wordt overgebracht door wrijving tussen grondplaat en betonblok, door afschuifspie en door buiging van ankerbouten en wrijving. De weerstand van bouten in afschuiving wordt analytisch beoordeeld. Wrijving en afschuifspie worden gemodelleerd als een volledige enkelpuntsbeperking in het vlak van de grondplaat - betoncontact.

Vervormingsstijfheid

De stijfheid van het betonblok kan voor het ontwerp van kolombases worden voorspeld als een elastische halve bol. Een Winkler-Pasternak ondergrondmodel wordt algemeen gebruikt voor een vereenvoudigde berekening van funderingen. De stijfheid van de ondergrond wordt bepaald met behulp van de elasticiteitsmodulus van beton en de effectieve hoogte van een ondergrond als:

\[ k = \frac{E_c}{(\alpha_1 + \upsilon) \sqrt{\frac{A_{eff}}{A_{ref}}}} \left( \frac{1}{\frac{h}{a_2 d} + a_3}+a_4 \right) \]

waar:

k – stijfheid van betonnen ondergrond in compressie
E_c – elasticiteitsmodulus van beton
υ – Poissoncoëfficiënt van het betonblok
A_eff – effectief gebied in compressie
A_ref = 1 m² – referentiegebied
d – breedte grondplaat
h – hoogte betonblok
a₁ = 1.65; a₂ = 0.5; a₃ = 0.3; a₄ = 1.0 – coëfficiënten

SI-eenheden moeten in de formule worden gebruikt, de resulterende eenheid is N/m³.

Overdracht van afschuifbelasting op de grondplaat

De afschuifbelasting op de grondplaat kan op drie manieren worden overgebracht:

Wrijving
Kluft
Ankers

De gebruiker kan de gemiddelde waarde kiezen door de werking van de grondplaat te bewerken. Een combinatie van middelen/gemiddelde waarden is in de software niet toegestaan, maar EN 1993-1-8 - Cl. 6.2.2 en Fib 58 - hoofdstuk 4.2 staat de combinatie van afschuiving door ankers en wrijving onder bepaalde voorwaarden toe. In het algemeen is het conservatief om wrijving te verwaarlozen in het ontwerp van de verankering, hoewel het in sommige gevallen kan leiden tot een onderschatting van de scheurvorming in beton op het bruikbaarheidsniveau. In de regel moet de wrijvingsweerstand worden verwaarloosd indien:

de dikte van de mortelvoeg overschrijdt de helft van de ankerdiameter,
de verankeringscapaciteit wordt bepaald door een bijna-randvoorwaarde
de verankering is bedoeld om weerstand te bieden aan aardbevingsbelastingen

De combinatie met een kluft mag nooit worden toegestaan wegens de vervormingscompatibiliteit.

Overdracht van afschuifbelasting door wrijving

De schuifweerstand is gelijk aan de veiligheidsfactor van de weerstand vermenigvuldigd met de wrijvingscoëfficiënt die kan worden aangepast in de Code setup en de drukbelasting. De drukbelasting omvat alle krachten, bv. in het geval van een kolombasis belast door drukkracht en buigend moment, kan de drukbelasting die gebruikt wordt voor de wrijvingsschuifweerstand hoger zijn dan de toegepaste drukkracht.

Overdracht van afschuifbelasting door kluft

De kluft wordt gesimuleerd als een in beton gevatte stomp onder de grondplaat. De afschuifbelasting wordt naar schatting overgedragen door een gelijkmatige verdeling van de belasting over het gehele deel van de kluft dat in het betonblok is ingebed, d.w.z. alle knooppunten van de kluft onder het betonoppervlak worden gelijkmatig belast. Het deel van de kluft boven het betonoppervlak in grout wordt niet verondersteld de afschuifbelasting over te dragen.

Men moet zich ervan bewust zijn dat de hefboomarm tussen de uitgeoefende afschuifbelasting (aan de grondplaat) en de afschuifweerstand (halve hoogte van de in beton ingebedde kluft) een buigend moment veroorzaakt dat moet worden overgebracht door drukkracht in beton en trekkracht in ankers.

De kluft bestaat uit schaal-eindige elementen en wordt gecontroleerd als gewone platen. Ook de lassen van de "kluft" aan de grondplaat worden gecontroleerd met standaardprocedures in IDEA Connection. Bij handmatige berekeningen wordt meestal uitgegaan van de ligger-theorie voor de kluft, hoewel dit niet nauwkeurig is omdat de lengte/breedte-verhouding bij de kluft zeer klein is. Daarom kan er een significant verschil zijn tussen IDEA Connection en de handmatige berekening.

Overdracht van afschuifbelasting door ankers

De afschuifweerstand wordt bepaald door de afschuifweerstand van de ankers. De staalweerstand van ankers heeft een elastoplastische belasting-vervormingscurve, maar de bezwijkwijzen van beton worden als volkomen bros beschouwd.

Analysis model of IDEA StatiCa

Rekenmodel voor staalverbindingen

De CBFEM-methode (Component Based Finite Element Model) maakt een snelle analyse mogelijk van verbindingen met verschillende vormen en configuraties.. Het model bestaat uit elementen waarop de belasting wordt uitgeoefend en productiebewerkingen (inclusief verstijvende staven) die dienen om elementen met elkaar te verbinden. Elementen moeten niet verward worden met productiebewerkingen omdat hun snijkanten verbonden zijn via koppelingen met het verbindingsknoop, dus ze vervormen niet goed als ze gebruikt worden in plaats van productiebewerkingen (verstijvende staven).

Het geanalyseerde FEM-model wordt automatisch gegenereerd. De ontwerper maakt het FEM-model niet, hij maakt de verbinding met behulp van productiebewerkingen - zie de afbeelding.

Productiebewerkingen/items die kunnen worden gebruikt om de verbinding te construeren

Elke productiebewerking voegt nieuwe onderdelen toe aan de verbinding - sneden, platen, bouten, lassen.

Dragende elementen en ondersteuningen

Eén element van de verbinding is altijd ingesteld als "dragend". Alle andere elementen zijn "verbonden". Het dragende element kan gekozen worden door de ontwerper. Het dragende element kan "doorgaand" of "beëindigd" zijn in de verbinding. "Beëindigde" elementen worden aan één kant ondersteund en "doorgaande" elementen worden aan beide uiteinden ondersteund.

Er bestaan verschillende types verbonden elementen, afhankelijk van de last die het element kan dragen:

Type N-Vy-Vz-Mx-My-Mz – het element is in staat om alle 6 componenten van interne krachten over te brengen
Type N-Vy-Mz – het element kan alleen lasten overbrengen in het XY-vlak - interne krachten N, V_y, M_z
Type N-Vz-My – het element kan alleen lasten overbrengen in het XZ-vlak - interne krachten N, V_z, M_y
Type N-Vy-Vz – het element kan alleen normaalkracht N en dwarskrachten V_y en V_z overbrengen

Plaat op plaat verbinding brengt alle componenten van interne krachten over

De lipplaatverbinding kan alleen lasten overbrengen in het XZ-vlak - interne krachten N, V_z, M_y

Schetsplaat - verbinding van vakwerkstaaf kan alleen axiale kracht N en dwarskrachten Vy en Vz overbrengen

Elke verbinding is in evenwicht tijdens de analyse van de raamconstructie. Als de eindkrachten van de individuele elementen worden toegepast op het gedetailleerde CBFEM-model, wordt er ook aan de evenwichtstoestand voldaan. Het zou dus niet nodig zijn om steunen te definiëren in het rekenmodel. Om praktische redenen wordt de steun die alle verplaatsingen weerstaat, echter gedefinieerd in het eerste uiteinde van het dragende element. Het beïnvloedt noch de spanningstoestand noch de interne krachten in de verbinding, alleen de presentatie van vervormingen.

Aan de uiteinden van de verbonden elementen worden geschikte ondersteuningstypes gedefinieerd die rekening houden met het type van de individuele elementen om het optreden van instabiele mechanismen te voorkomen.

De standaardlengte van elk element is twee keer de hoogte. De lengte van een element moet minstens 1× de hoogte van het element zijn na de laatste bewerking (las, opening, verstijver enz.) omwille van de correcte vervormingen na de koppelingen die het gesneden uiteinde van een element verbinden met de verbindingsknoop.

Knoopevenwicht in het 3D FEM-model

De lasten op elke knoop in het constructiemodel moeten in evenwicht zijn. Eventuele onevenwichtige krachten worden opgevangen door steunpunten. Het wordt aanbevolen om een belastingcombinatie te gebruiken in plaats van een omhullende met interne krachten.

Elke knoop van het 3D FEM-model moet in evenwicht zijn. De evenwichtsvereiste is correct, maar niet noodzakelijk voor het ontwerp van eenvoudige verbindingen. Eén element van de verbinding is altijd "dragend" en de andere zijn verbonden. Als alleen de verbinding van verbonden elementen wordt gecontroleerd, is het niet nodig om het evenwicht te bewaren. Er zijn dus twee manieren beschikbaar om lasten in te voeren:

Versimpeld - bij deze modus wordt het dragende element ondersteund (doorgaande ligger aan beide zijden) en wordt de last niet gedefinieerd op het element.
Expert (exact met evenwichtscontrole) - het dragende element wordt aan één kant ondersteund, de lasten worden op alle elementen toegepast en het evenwicht moet worden gevonden.

De modus kan worden aangepast in de werkbalk Lasten in evenwicht.

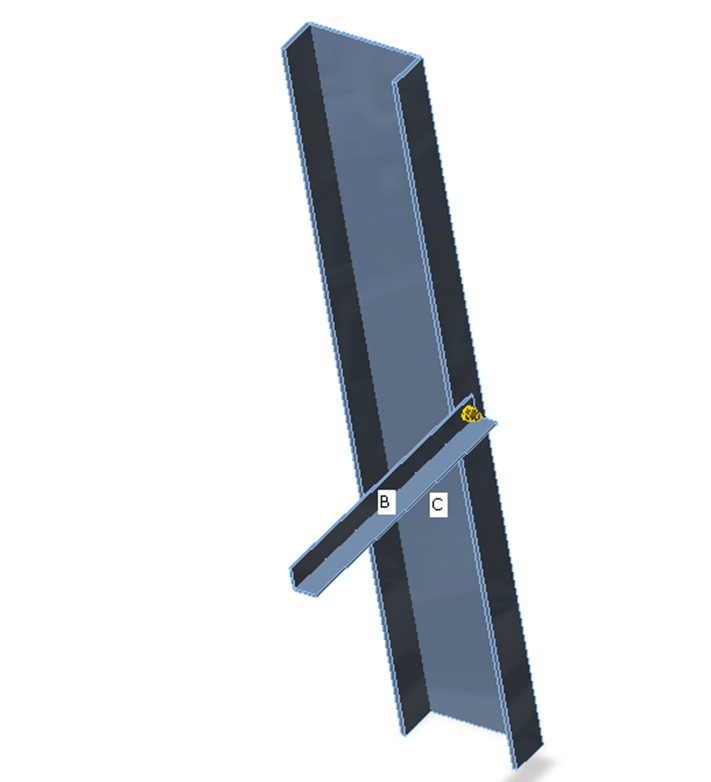
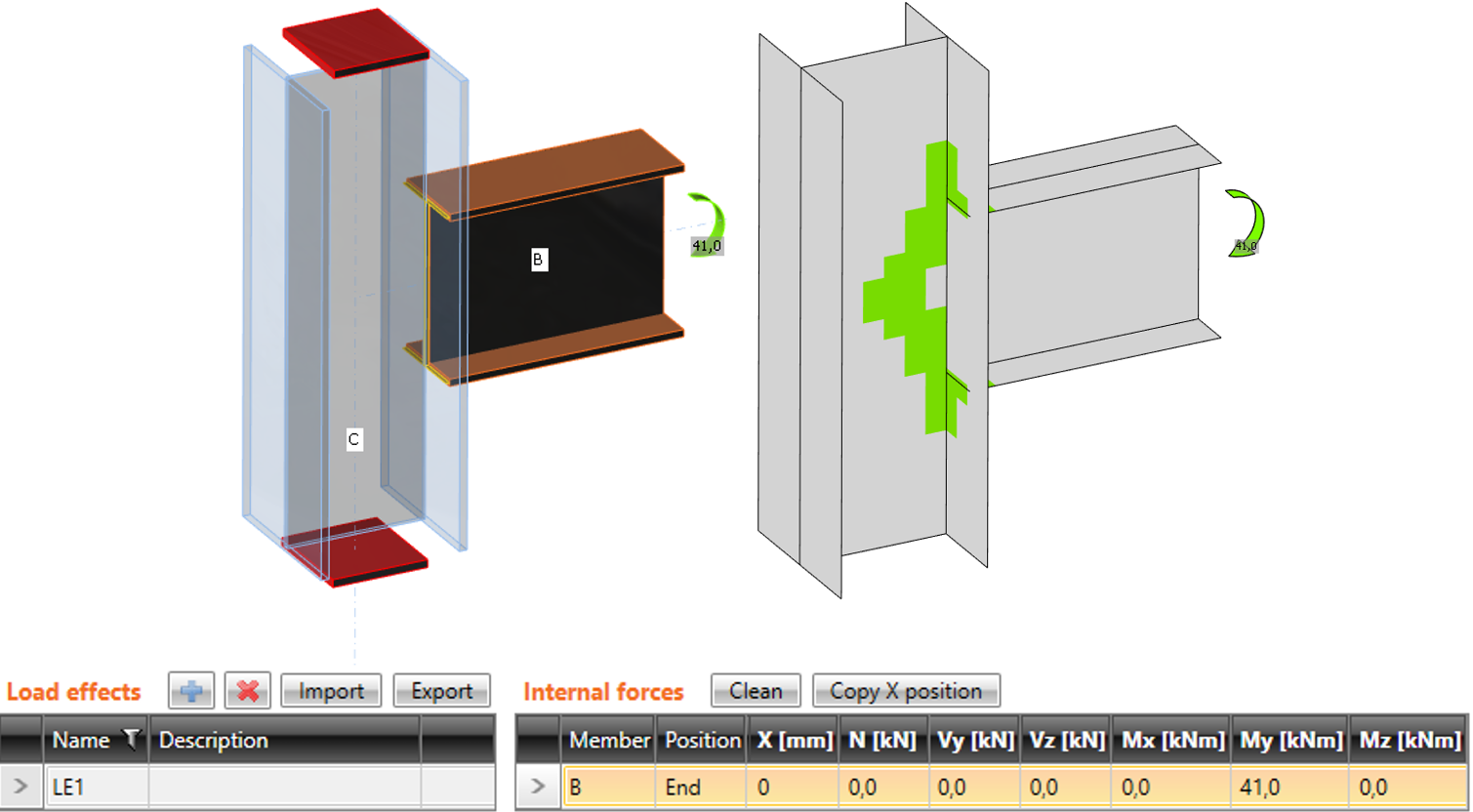
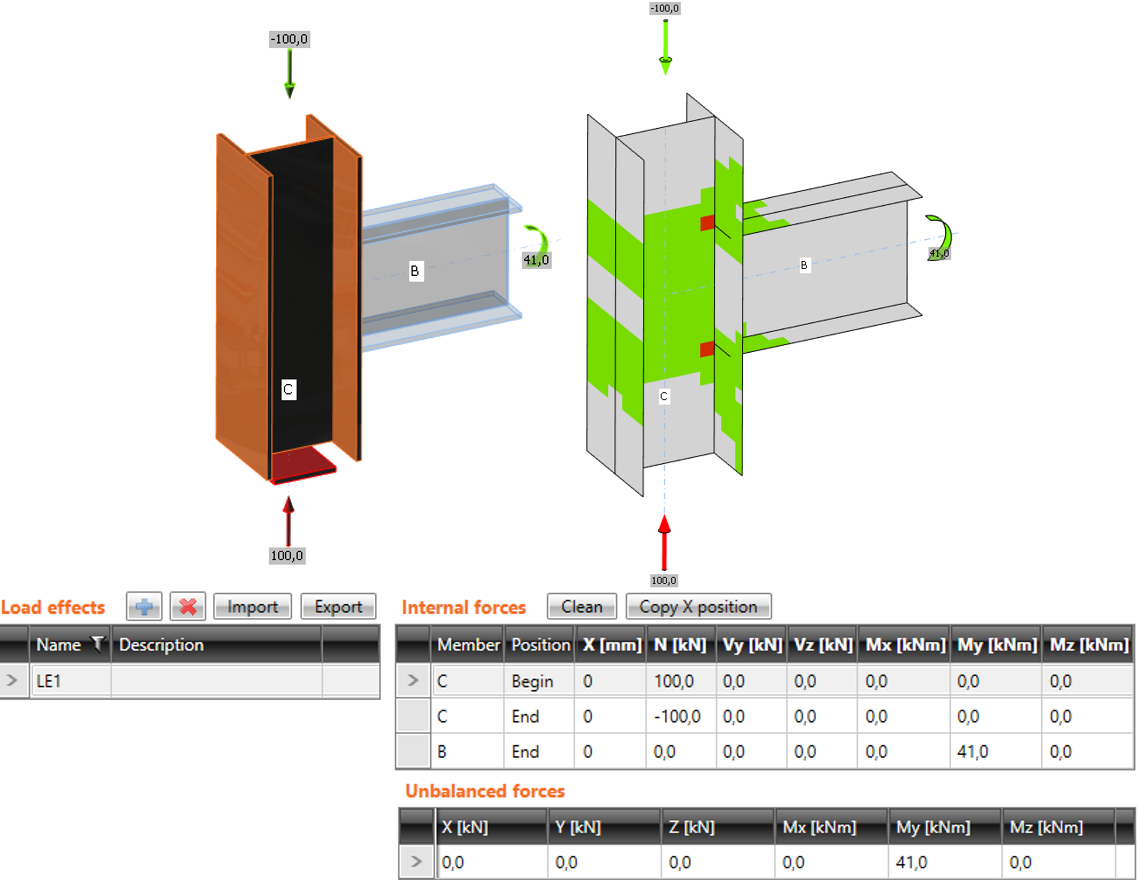
Het verschil tussen de modi wordt getoond in het volgende voorbeeld van een T-verbinding. De ligger wordt belast door het eindbuigmoment van 41 kNm. Er is ook een samendrukkende normaalkracht van 100 kN in de kolom. In het geval van versimpelde modus wordt geen rekening gehouden met de normaalkracht omdat de kolom aan beide uiteinden wordt ondersteund. Het programma toont alleen het effect van het buigend moment van de ligger. Effecten van de normaalkracht worden alleen geanalyseerd in de volledige modus en worden getoond in de resultaten.

Versimpelde invoer: er wordt GEEN rekening gehouden met de normaalkracht in de kolom

Expert invoer: er wordt rekening gehouden met de normaalkracht in de kolom

De versimpelde methode is eenvoudiger voor de gebruiker, maar kan alleen gebruikt worden als de gebruiker geïnteresseerd is in het bestuderen van verbindingsitems en niet het gedrag van de hele verbinding.

In gevallen waar het dragende element zwaar wordt belast en dicht bij zijn grenscapaciteit zit, is de expert modus met alle interne krachten in de verbinding noodzakelijk.

Loads

The end forces of a member of the frame analysis model are transferred to the ends of member segments. Eccentricities of the members caused by the joint design are respected during transfer.

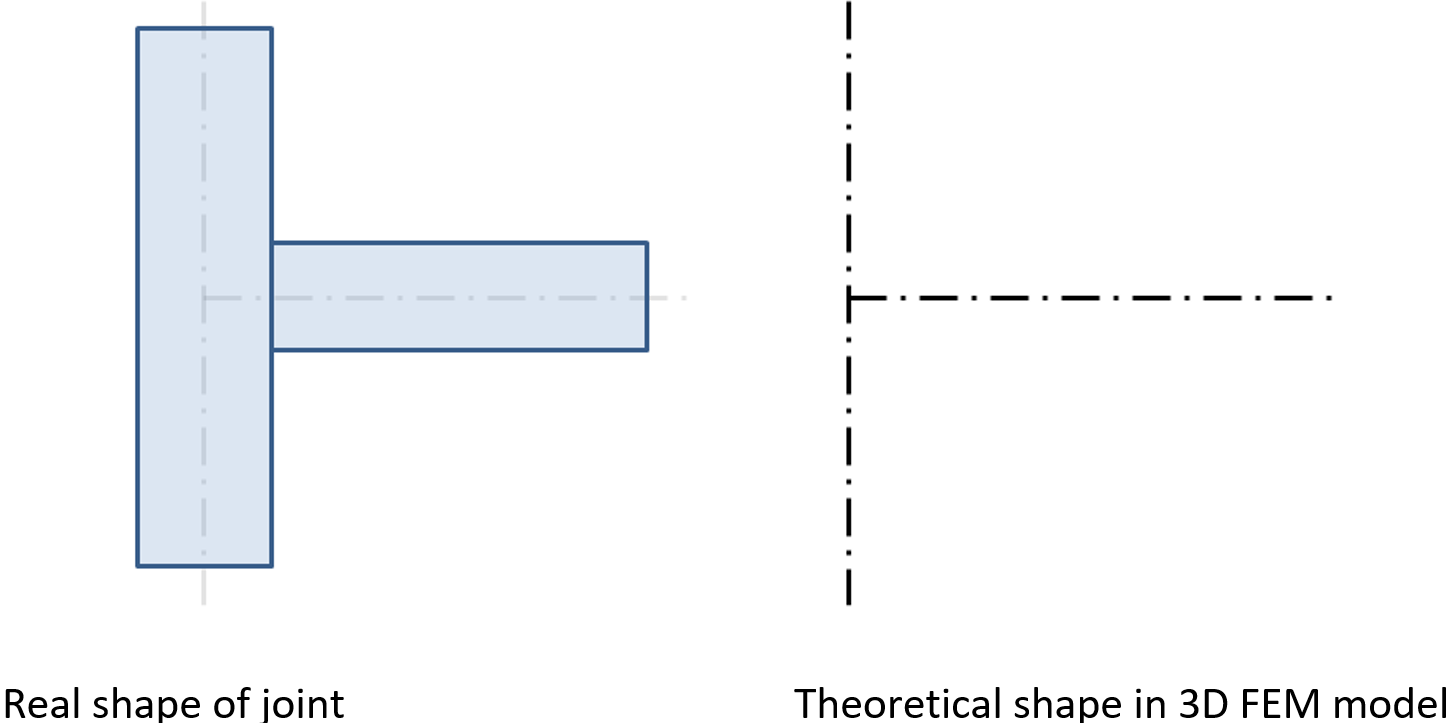
The analysis model created by CBFEM method corresponds to the real joint very precisely, whereas the analysis of internal forces is performed on much idealized 3D FEM bar model, where individual beams are modeled using center lines and the joints are modeled using immaterial nodes.

Joint of a vertical column and a horizontal beam

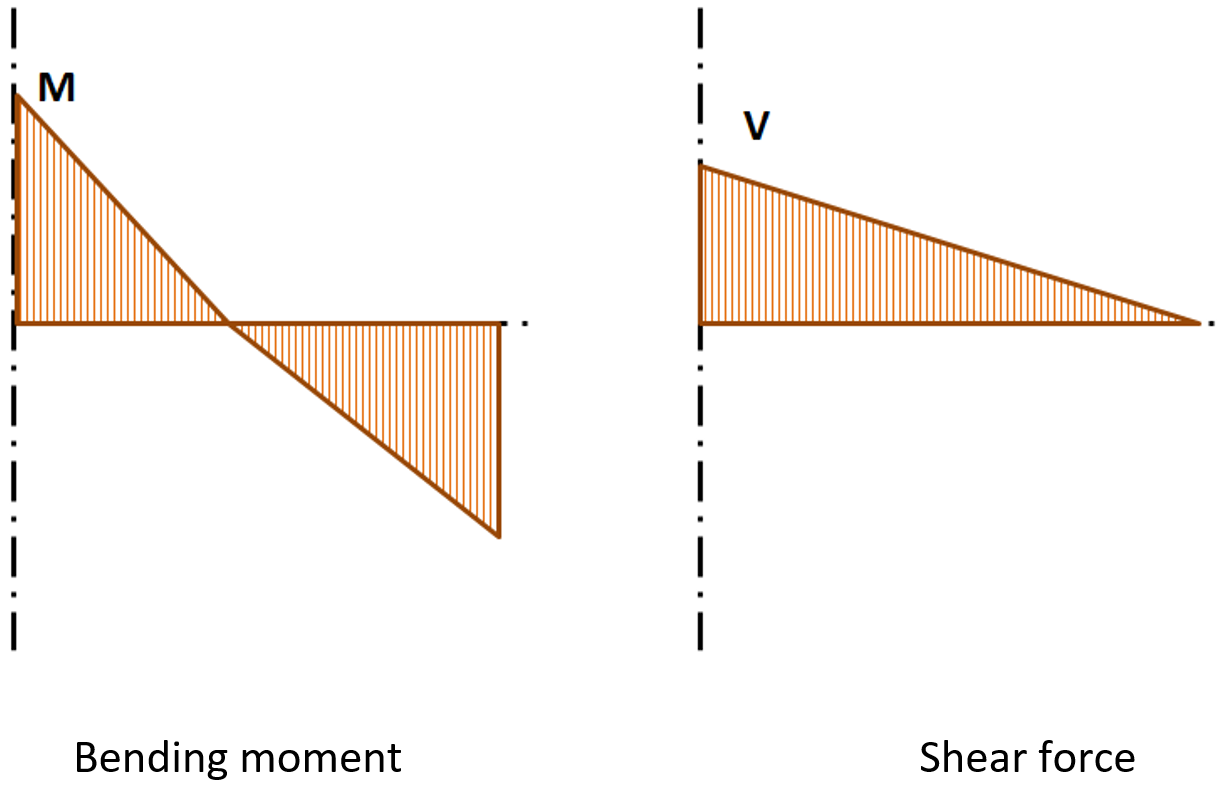
The internal forces are analyzed using 1D members in the 3D model. There is an example of the internal forces in the following figure.

Internal forces in horizontal beam; M and V are the end forces at joint

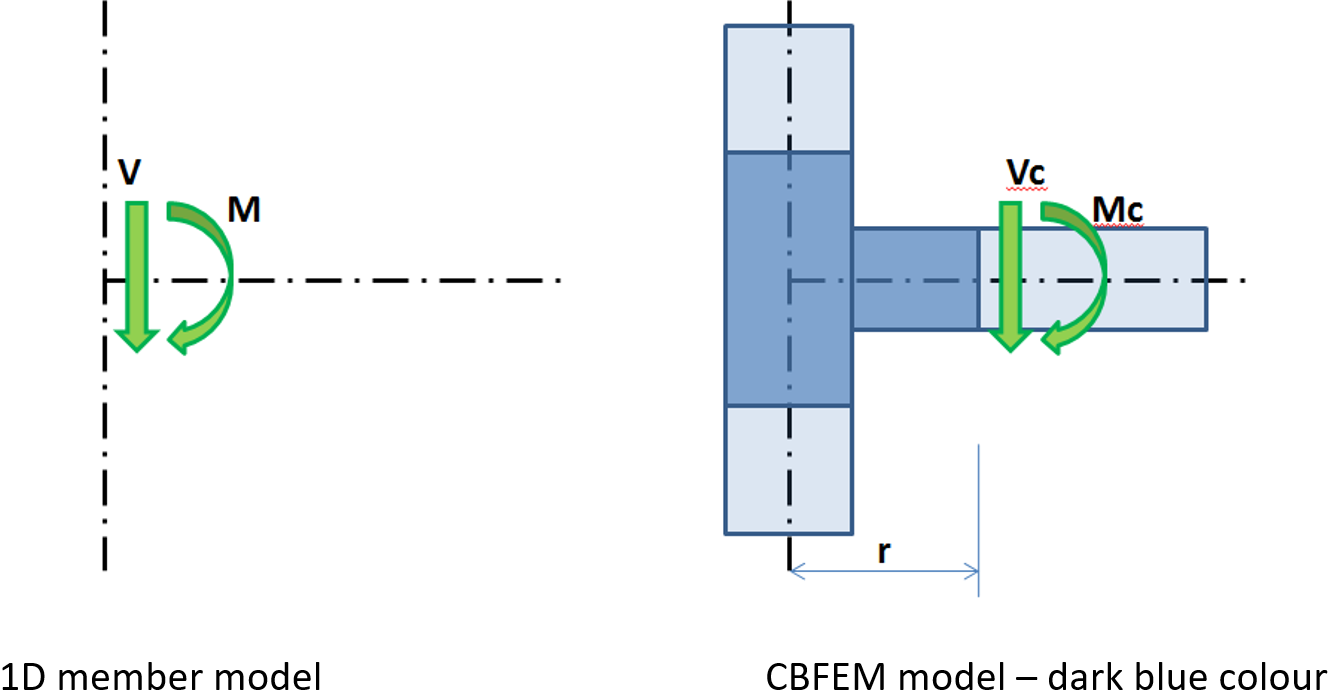
The effects caused by a member on the joint are important to design the joint (connection). The effects are illustrated in the following figure:

Effects of the member on the joint; CBFEM model is drawn in dark blue color

Moment M and shear force V act in the theoretical joint. The point of the theoretical joint does not exist in the CBFEM model, thus the load cannot be applied here. The model must be loaded by actions M and V which have to be transferred to the end of segment in the distance r

M_c = M – V ∙ r

V_c = V

In the CBFEM model, the end section of the segment is loaded by moment M_c and force V_c.

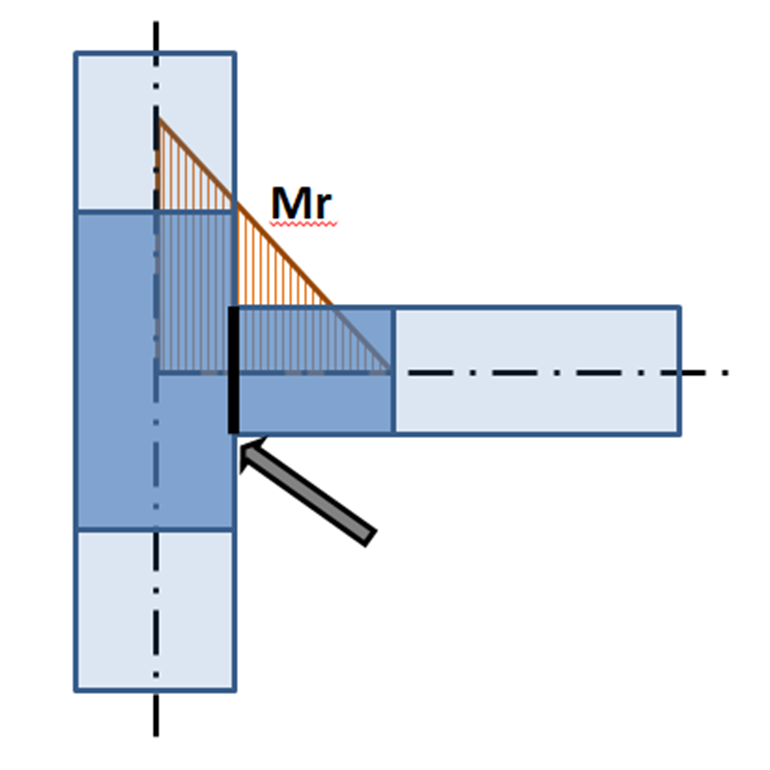
When designing the joint, its real position relative to the theoretical point of joint must be determined and respected. The internal forces in the position of the real joint are mostly different from the internal forces in the theoretical point of joint. Thanks to the precise CBFEM model, the design is performed on reduced forces – see moment M_r in the following figure:

Bending moment on CBFEM model: The arrow points to the real position of connection

When loading the joint, it must be respected that the solution of the real joint must correspond to the theoretical model used for calculation of internal forces. This is fulfilled for rigid joints but the situation may be completely different for hinges.

Position of hinge in theoretical 3D FEM model and in the real structure

It is illustrated in the previous figure that the position of the hinge in the theoretical 1D members model differs from the real position in the structure. The theoretical model does not correspond to reality. When applying the calculated internal forces, a significant bending moment is applied to the shifted joint and the designed joint is overlarge or cannot be designed either. The solution is simple – both models must correspond. Either the hinge in 1D member model must be defined in the proper position or the shear force must be shifted to get a zero moment in the position of the hinge.

Shifted distribution of bending moment on beam: zero moment is at the position of the hinge

The shift of the shear force can be defined in the table for the internal forces definition.

The location of load effect has a big influence on the correct design of the connection. To avoid all misunderstandings, we allow the user to select from three options – Node / Bolts / Position.

Note that when selecting the Node option, the forces are applied at the end of a selected member which is usually at the theoretical node unless the offset of the selected member is set in geometry.

Import loads from FEA programs

IDEA StatiCa enables to import internal forces from third-party FEA programs. FEA programs use an envelope of internal forces from combinations. IDEA StatiCa Connection is a program which resolves steel joint nonlinearly (elastic/plastic material model). Therefore, the envelope combinations cannot be used. IDEA StatiCa searches for extremes of internal forces (N, V_y, V_z, M_x, M_y, M_z) in all combinations at the ends of all members connected to the joint. For each such extreme value, also all other internal forces from that combination in all remaining members are used. Idea StatiCa determines the worst combination for each component (plate, weld, bolt etc.) in the connection.

The user can modify this list of load cases. He can work with combinations in the wizard (or BIM) or he can delete some cases directly in IDEA StatiCa Connection.

Warning!

It is necessary to take into account unbalanced internal forces during the import. This can happen in following cases:

Nodal force was applied to the position of the investigated node. The software cannot detect which member should transfer this nodal force and, therefore, it is not taken into account in the analysis model. Solution: Do not use nodal forces in global analysis. If necessary, the force must be manually added to a selected member as a normal or shear force.
Loaded, non-steel (usually timber or concrete) member is connected to the investigated node. Such member is not considered in the analysis and its internal forces are ignored in the analysis. Solution: Replace the concrete member with a concrete block and anchorage.
The node is a part of a slab or a wall (usually from concrete). The slab or the wall is not part of the model and its internal forces are ignored. Solution: Replace the concrete slab or wall with a concrete block and anchorage.
Some members are connected to the investigated node via rigid links. Such members are not included in the model and their internal forces are ignored. Solution: Add these members into the list of connected members manually.
Seismic load cases are analysed in the software. Most FEA software offer the modal analysis to solve seismicity. The results of internal forces of seismic load cases provide usually only internal force envelopes in sections. Due to the evaluation method (square root of the sum of squares – SRSS), the internal forces are all positive and it is not possible to find the forces matching to the selected extreme. It is not possible to achieve a balance of internal forces. Solution: Change the positive sign of some internal forces manually.

Sterkteanalyse van staalverbindingen

Sterkteanalyse is de belangrijkste analyse van verbindingen. Rekcontroles van platen samen met codecontroles van componenten worden uitgevoerd door een elastisch-plastische analyse.

De analyse van verbindingen is materieel niet-lineair. De belastingstoenames worden geleidelijk toegepast en de spanningstoestand wordt opgezocht. Er zijn twee optionele analysemodi in IDEA StatiCa Connection:

De reactie van de constructie (verbinding) op de totale belasting. Alle gedefinieerde belasting (100%) wordt in deze modus toegepast, en de bijbehorende toestand van spanning en vervorming wordt berekend.

Beëindiging van de analyse bij het bereiken van de uiterste grenstoestand. Het selectievakje in Code setup "Stop at limit strain" (Stoppen bij grensrek) moet worden aangevinkt. De toestand wordt gevonden wanneer de plastische rek de gedefinieerde limiet bereikt. In het geval dat de gedefinieerde belasting hoger is dan de berekende capaciteit, wordt de analyse gemarkeerd als niet voldoende en wordt het percentage van de gebruikte belasting afgedrukt. Denk eraan dat de analytische weerstand van onderdelen, bijvoorbeeld van bouten, overschreden kan worden.

De tweede modus is meer geschikt voor praktisch ontwerp. De eerste heeft de voorkeur voor een gedetailleerde analyse van complexe verbindingen.

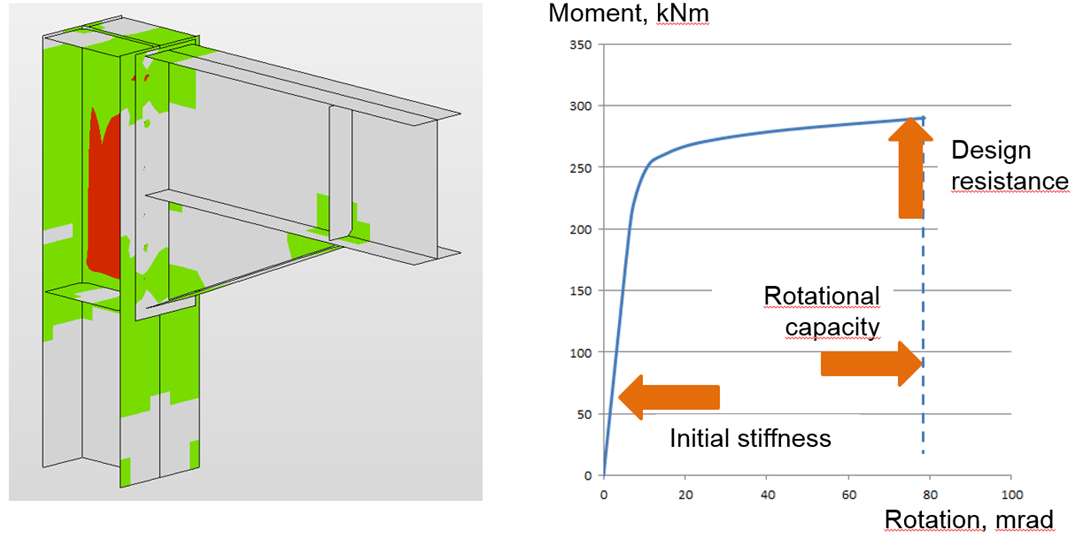
Stijfheidsberekening en vervormingscapaciteit

Verbindingen worden geclassificeerd op basis van stijfheid tot stijf, flexibel of scharnierend. De ingenieur moet ervoor zorgen dat de stijfheid van de verbinding overeenkomt met de stijfheid waarvan uitgegaan wordt in de CAE-software.

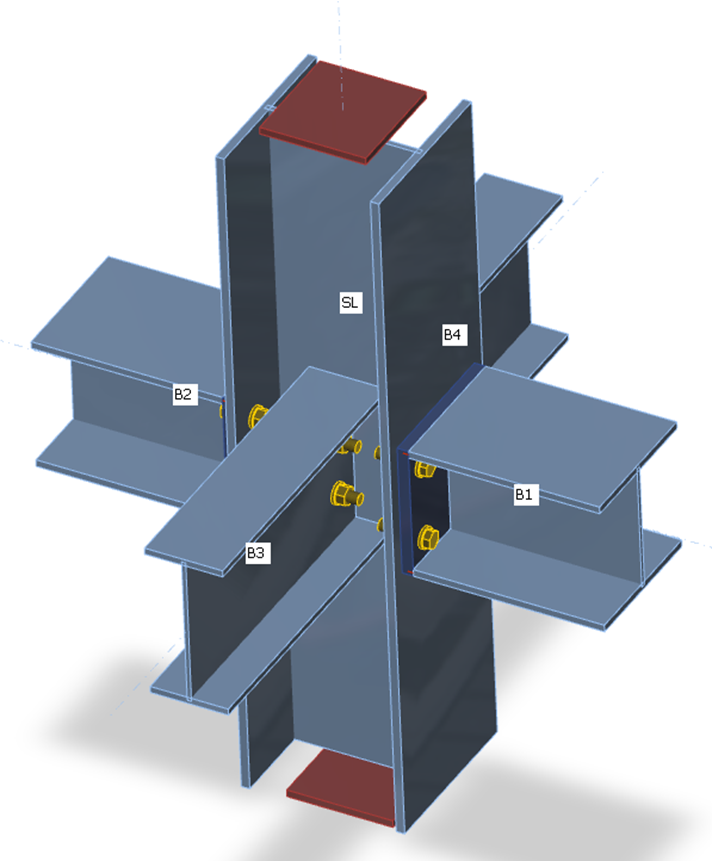
De CBFEM-methode maakt het mogelijk om de stijfheid van de verbinding van individuele aangesloten staven te berekenen. Voor de juiste stijfheidsberekening moet voor elke geanalyseerde staaf een afzonderlijk analysemodel worden gemaakt. Vervolgens wordt de stijfheidsberekening niet beïnvloed door de stijfheid van andere verbindingselementen, maar alleen door het knooppunt zelf en de constructie van de verbinding van de berekende staaf. Terwijl de dragende staaf wordt ondersteund voor de sterkteberekening (staaf SL in de onderstaande afbeelding), worden alle staven behalve de geanalyseerde ondersteund door de stijfheidsberekening (zie twee afbeeldingen hieronder voor stijfheidsberekening van staven B1 en B3).

Sterkteberekening van de verbinding met opleggingen in IDEA CONNECTION

Opleggingen op staven voor sterkteberekening

Stijfheidsberekening van de verbinding met berekende staaf in plaats van dragende staaf

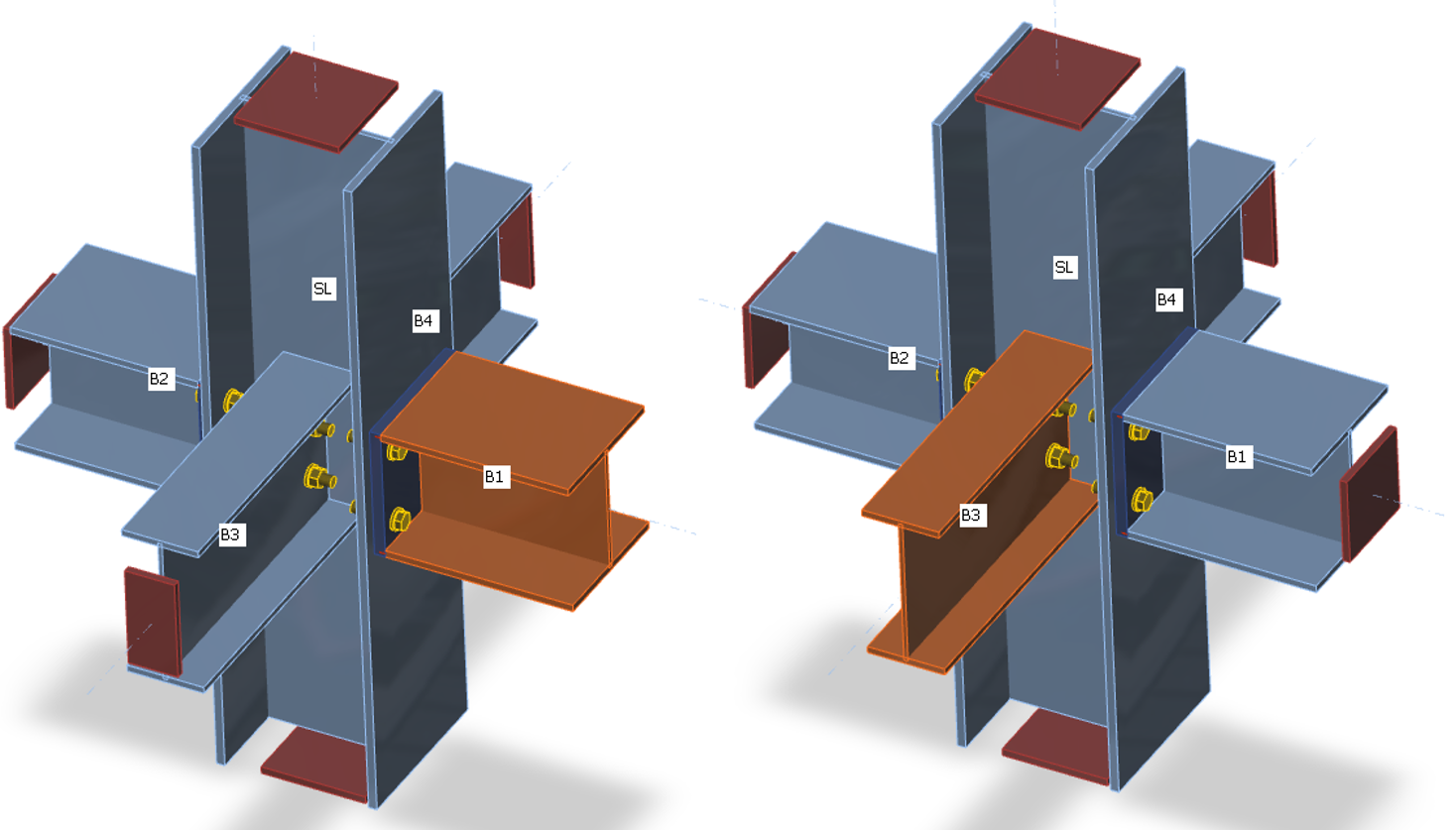
Opleggingen op staven voor stijfheidsberekening van staaf B1

Opleggingen op staven voor stijfheidsberekening van staaf B3

Belastingen kunnen alleen op de berekende staaf worden toegepast. Als het buigmoment My is gedefinieerd, wordt de rotatiestijfheid rond de y-as geanalyseerd. Als het buigmoment Mz is gedefinieerd, wordt de rotatiestijfheid om de z-as geanalyseerd. Als axiale kracht N is gedefinieerd, wordt de axiale stijfheid van de verbinding geanalyseerd.

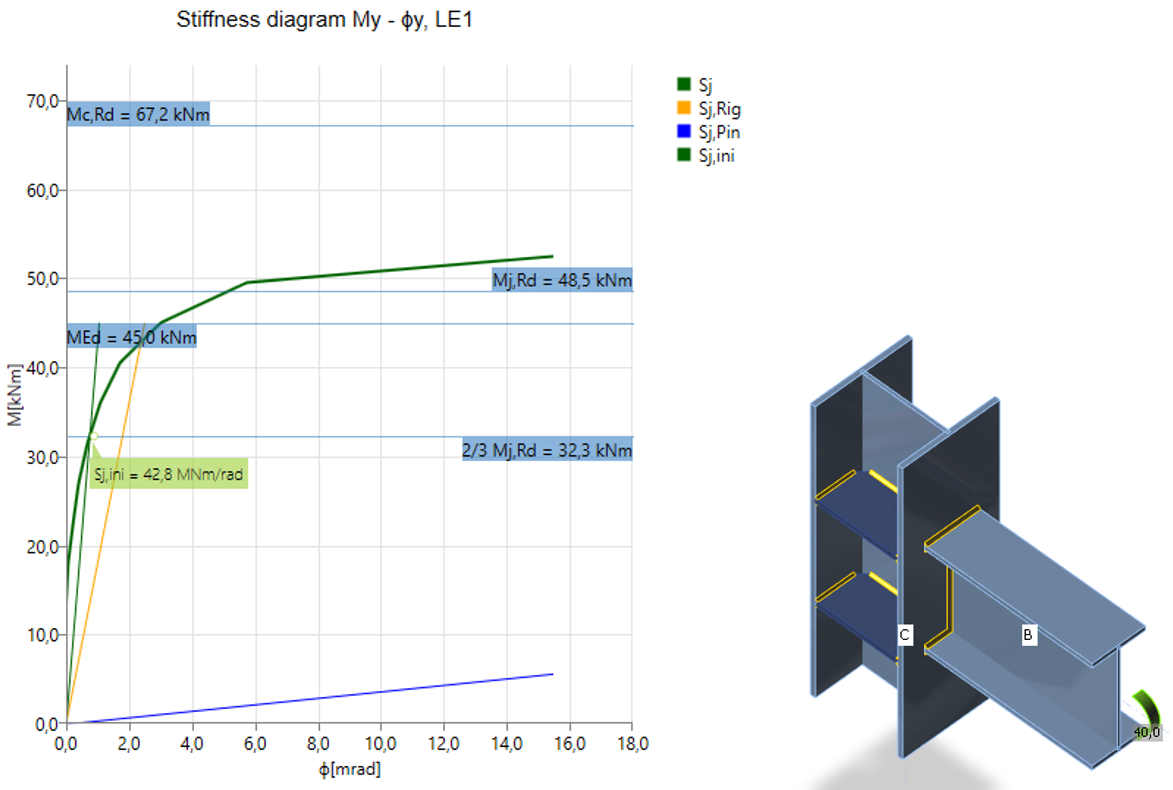
Het programma genereert automatisch een compleet diagram, het wordt direct weergegeven in de resultaten en kan worden toegevoegd aan het rapport. Rotatie- of axiale stijfheid kan worden bestudeerd voor specifieke ontwerpbelastingen. IDEA StatiCa Connection kan ook omgaan met de interactie van de andere snedekrachten.

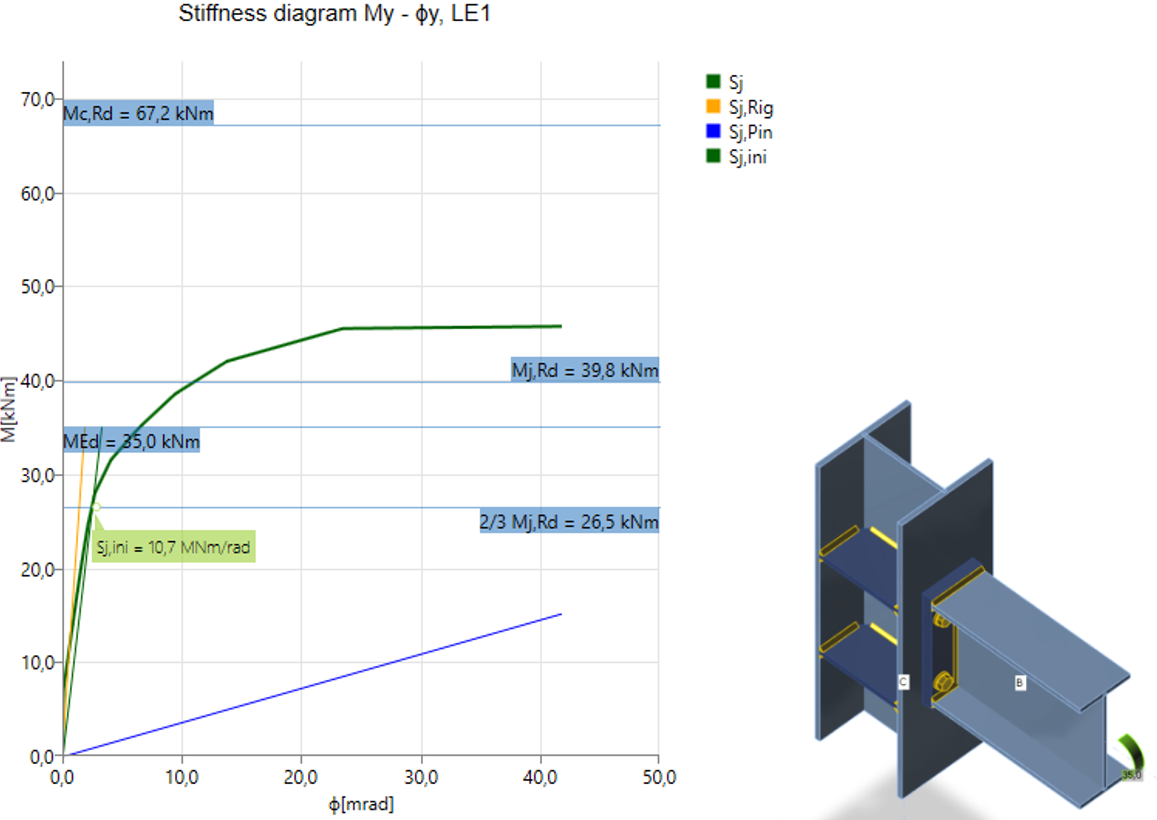
Het diagram laat zien :

Niveau van ontwerpbelasting MEd
Grenswaarde van de capaciteit van de verbinding voor 5% equivalente rek, Mj, Rd; limiet voor plastische rek kan worden gewijzigd in Norm-instellingen
Grenswaarde van capaciteit van aangesloten staaf (ook nuttig voor seismisch ontwerp) Mc, Rd
2/3 van de limietcapaciteit voor de berekening van de initiële stijfheid
Waarde van initiële stijfheid Sj, ini
Waarde van secant stijfheid Sjs ( op basis van de MEd)
Limieten voor de classificatie van verbinding - stijf en scharnierend
Rotatievervorming Φ
Rotatiecapaciteit Φc

Stijve verbinding in moment rotatie diagram in IDEA CONNECTION

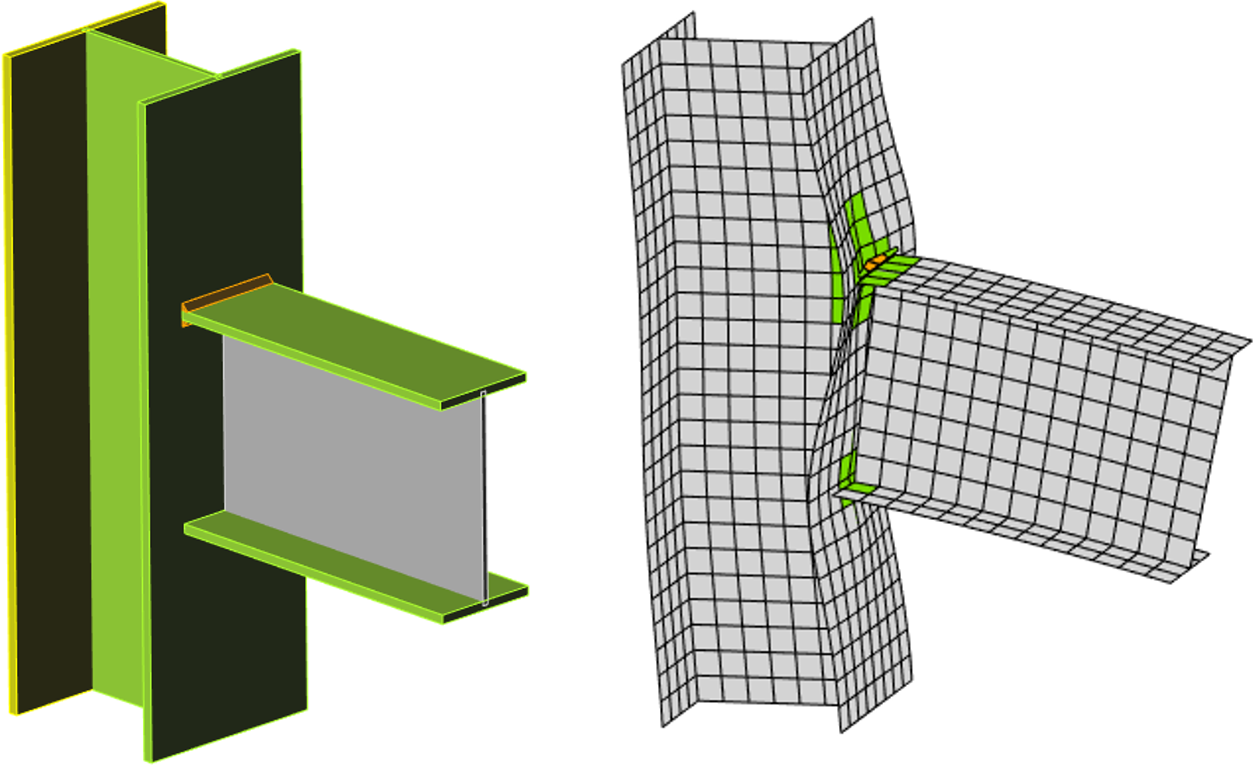
Stijve gelaste verbinding

flexibele geboute verbinding in IDEA CONNECTION

Felxibele geboute verbinding

Ontwerpweerstand van de verbinding in IDEA CONNECTION

Na het bereiken van de 5% rek in het kolomlijf bij afschuiving, worden de plastische zones snel meer.

The joint is classified according to its stiffness into rigid, semi-rigid or pinned category according to the relevant code. The theoretical length of the member can be set for the analyzed member:

De verbinding wordt op basis van zijn stijfheid geclassificeerd in starre, semi-rigide of scharnierende categorie volgens de relevante norm. De theoretische lengte van de staaf kan worden ingesteld voor de berekende staaf:

theoretische liggerlengte in IDEA CONNECTION

Vervormings capaciteit

De vervormingscapaciteit / ductiliteit δCd hoort bij de weerstand en de stijfheid bij de drie basisparameters die het gedrag van verbindingen beschrijven. Bij momentvaste verbindingen wordt de ductiliteit bereikt door voldoende rotatiecapaciteit φCd. De vervormings- / rotatie capaciteit wordt voor elke aansluiting in de verbinding afzonderlijk berekend.

De schatting van de rotatiecapaciteit is belangrijk bij verbindingen die zijn blootgesteld aan seismiek, zie Gioncu en Mazzolani (2002) en Grecea (2004) en bij extreme belasting, zie Sherbourne en Bahaari (1994 en 1996). De vervormingscapaciteit van componenten is bestudeerd vanaf het einde van de vorige eeuw (Foley en Vinnakota, 1995). Faella et al. (2000) voerden tests uit op T-stubs en leidden de analytische formules af voor het vervormingsvermogen. Kuhlmann en Kuhnemund (2000) voerden tests uit op het kolomlijf dat werd onderworpen aan transversale druk op verschillende niveaus van axiale compressiekracht in de kolom. Da Silva et al. (2002) voorspelde vervormingscapaciteit op verschillende niveaus van axiale kracht in de verbonden staaf. Op basis van de testresultaten gecombineerd met FE-analyse, worden vervormingscapaciteiten voor de basiscomponenten vastgesteld door analytische modellen van Beg et al. (2004). In het werk worden componenten weergegeven door niet-lineaire veren en op de juiste manier gecombineerd om de rotatiecapaciteit van de kopplaat aansluitingenin de verbinding te bepalen, met een verlengde of vlakke kopplaat en lasverbindingen. Voor deze verbindingen werden de belangrijkste componenten die significant kunnen bijdragen aan het rotatievermogen herkend als het kolomlijf onder druk, het kolomlijf onder trek, het kolomlijf in afschuiving, de kolomflens onder buiging en de kopplaat onder buiging. Componenten die verband houden met het kolomlijf zijn alleen relevant als er geen verstijvers in de kolom zijn die weerstand bieden aan compressie-, trek- of afschuifkrachten. De aanwezigheid van een verstijver elimineert de corresponderende component, en zijn bijdrage aan het rotatievermogen van de verbinding kan daarom worden verwaarloosd. Kopplaten en kolomflenzen zijn alleen van belang voor kopplaatverbindingen waarbij de componenten fungeren als een T-stub, waarbij ook de vervormingscapaciteit van de bouten onder trek is inbegrepen. De vragen en grenzen van de vervormingscapaciteit van verbindingen van hogesterkte-staal werden bestudeerd door Girao et al. (2004).

Weerstandsberekening van staalverbindingen

De weerstandsberekening is een onderdeel van een seismisch ontwerp. Als men vertrouwt op de ductiliteit van een constructie, moet de weerstandsberekening worden uitgevoerd.

Het doel van de weerstandsberekening is om te bevestigen dat een gebouw gecontroleerd ductiel gedrag ondergaat om instorting te voorkomen bij een aardbeving.

Er wordt een dissipatief onderdeel geselecteerd met een verhoogde sterkte en een gewijzigd materiaal diagram. Een oversterkte factor \(\gamma_{ov}\) wordt gedefinieerd in Materialen, en een verhardingsfactor \(\gamma_{sh}\) in de werking van het dissipatief onderdeel. Let erop dat de nomenclatuur tussen de normen verschilt. Een dissipatief onderdeel is uitgesloten van de rekcontrole van platen.

seismisch materiaaldiagram voor seimisch ontwerp van een staalverbinding

Gewijzigd materiaal diagram voor dissipatief onderdeel

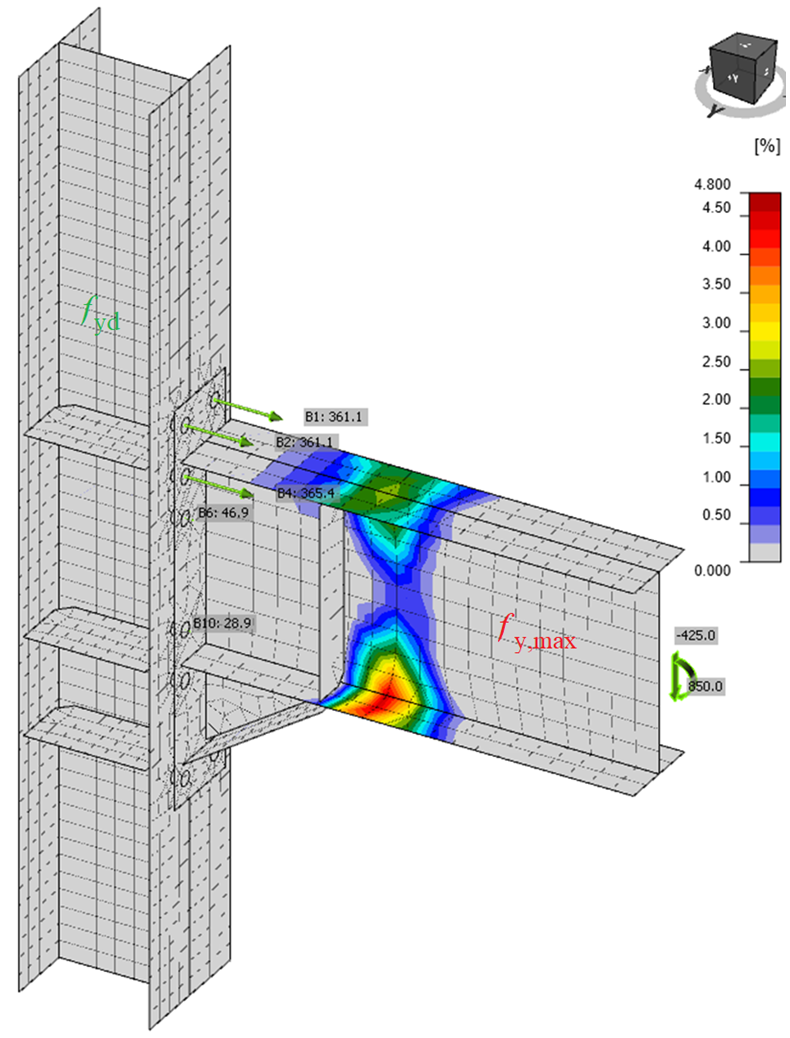
IDEA StatiCa Connection controleert de verbinding op toegepaste ontwerpbelasting die een plastisch scharnier moet creëren in het geselecteerde dissipatieve onderdeel, meestal de balk. De plastische rek in het dissipatieve onderdeel moet ongeveer 5% zijn. Dit kan dienen als bevestiging dat de grootte en positie van de belastingen juist zijn bepaald.

Plastisch scharnier gecreëerd op de bedoelde plaats van het dissipatieve onderdeel - de balk

De ondersteuningen van het doorlopende element worden automatisch gedefinieerd als gesteund aan één uiteinde en met ingehouden momenten aan het andere uiteinde. Op deze manier kan de doorlopende kolom worden belast door de normaalkracht en dwarskrachten, en ook kan één zijde zijwaarts bewegen zodat het bezwijken van de kolomlijf in afschuiving aan het licht komt.

Let erop dat detaillering erg belangrijk is voor seismisch bestendige verbindingen, maar niet wordt gecontroleerd in IDEA StatiCa.

Weerstand van de verbinding

Weerstand van de verbinding helpt om reserve in de verbindingsweerstand in te schatten.

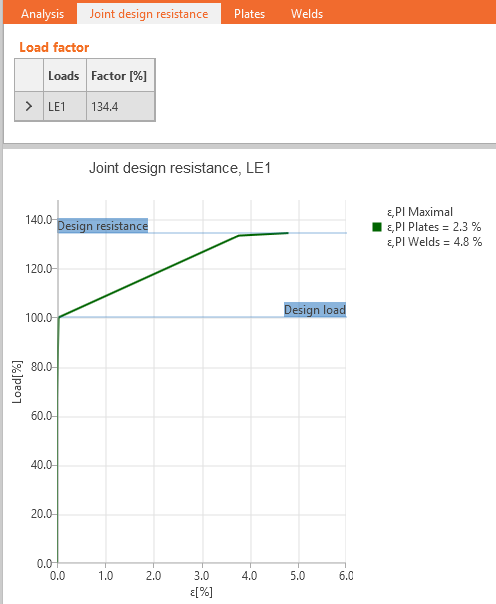
De ontwerper lost meestal de taak op om de verbinding zo te ontwerpen om de ontwerpbelasting over te dragen. Maar het is ook handig om te weten hoe ver het ontwerp van de grenstoestand is, dus hoe groot de reserve in het ontwerp is en hoe veilig het is. Dit kan eenvoudig worden gedaan door het berekeningstype DR - Weerstand van de verbinding.

De gebruiker voert de ontwerpbelasting in zoals in een standaardontwerp. De software verhoogt automatisch alle belastingscomponenten proportioneel totdat een van de meegeleverde controles niet voldoet.

DR-analyses voeren controles uit op de volgende onderdelen:

Plastische spanning in platen
Bouten - afschuiving, spanning en combinatie van spanning en afschuiving
Ankers – trek- en afschuifweerstand van staal
Lassen

Houd er rekening mee dat andere componenten die niet in de bovenstaande lijst zijn opgenomen, niet worden gecontroleerd vanwege onbekende richtingen van krachten in componenten. Voer daarom altijd een EPS-analyse uit om er zeker van te zijn dat alle controles correct worden uitgevoerd.

De gebruiker krijgt de verhouding te zien in procenten tussen de maximale belasting en de ontwerpbelasting. Er wordt ook een eenvoudige grafiek gegeven.

UItvoer van ontwerpweerstand van de staalverbinding van IDEA CONNECTION

De resultaten van door de gebruiker gedefinieerde belastinggevallen worden weergegeven, tenzij de gezamenlijke ontwerpweerstandsfactor kleiner is dan 100 %, wat betekent dat de berekening niet voldoet aan de ontwerpbelasting en de laatste geconvergeerde stap van het belastinggeval wordt dan weergegeven.

Buckling analysis

Buckling is usually not an important issue in joints however, it should be checked that there are no buckling issues and the results of strength analysis, which uses only geometrically linear analysis, are correct.

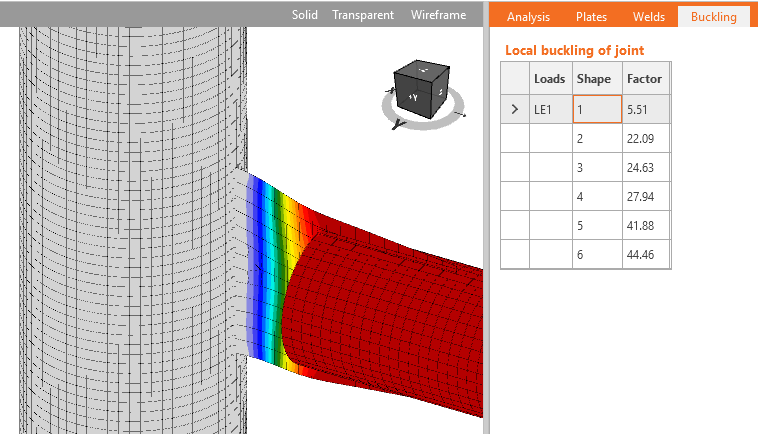
IDEA StatiCa Connection is able to perform linear buckling analysis of a model of a joint. The results are predicted in buckling modes. Critical load, at which buckling of perfect model occurs, is calculated for each buckling mode. Critical load is presented by multipliers of the load acting on the joint. According to the buckling mode and critical load multiplier, the user can determine the safe buckling design.

Some codes, e.g. Eurocode (EN 1993-1-1, Chapter 5.2.1), recommend a critical load multiplier higher than 15 for bar models of structures. If the critical load multiplier is higher than 15, the code does not require buckling check of members.

For joints, the matter is different and the code does not provide any specific recommendation. Design of local buckling must be tackled in another way. Generally, the local buckling may be divided into three groups:

Plates connecting individual members
Stiffening plates in the joint – stiffeners, ribs, short haunches
Closed sections and thin-walled sections

Buckling of plates from group 1 affects the buckling shape of the whole member. Therefore, it is recommended to apply the same rules as for these members also to these plates, i.e. consider safe critical load multiplier 15 and higher. The engineer should verify that real execution of the joint corresponds to the boundary conditions of the model used for buckling analysis of the whole structure.

Plates from group 2 affect local buckling of the joint. For such plates, the safe boundary of critical load multiplier 15 is conservative, but specific guidance is missing in codes. The guidance is provided by research papers that recommend safe boundary of critical load multiplier equal to 3.

Buckling of plates and members from group 3 is very problematic and individual assessment of each particular case is necessary.

For plates with critical load multiplier smaller than suggested values (15 for group 1, 3 for group 2), plastic design cannot be used. Other methods that are not offered by IDEA StatiCa are necessary for their check.

The result of buckling analysis in IDEA Connection is not a definite check. The codes do not give sufficient guidance. The assessment requires engineering judgment and IDEA StatiCa provides unique tools not available in standard design software.

Gusset plate as an elongation of a truss – example of plate from group 1 for which buckling can be neglected if critical buckling factor is higher than 15

Examples of buckling shapes of plates from group 2 where the buckling can be neglected if critical buckling factor is higher than 3

The model used for buckling analysis is supported by different supports than set by the user in stress, strain analysis type (EPS). The bearing member stays fully supported. Model type of a beam set as N-Vy-Vz-Mx-My-Mz (free to move in stress, strain analysis type) is fully supported in buckling analysis. All other beam analysis types have restrained bending moments and normal force but are free to move sideways.

Model type N-Vy-Vz-Mx-My-Mz: supports in buckling model: N-Vy-Vz-Mx-My-Mz
Model type N-Vy-Vz: supports in buckling model: N-Mx-My-Mz
Model type N-Vz-My: supports in buckling model: N-Mx-My-Mz
Model type N-Vy-Mz: supports in buckling model: N-Mx-My-Mz

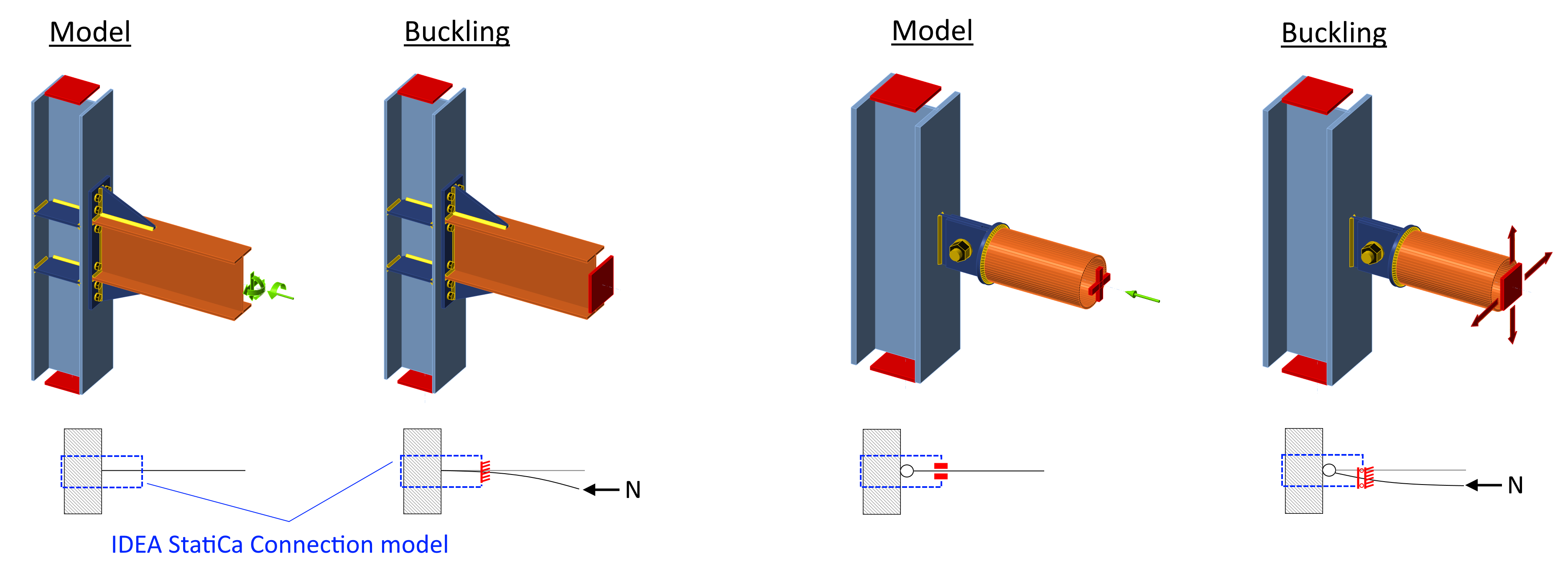
It is assumed that in case of rigid joint, user sets bending moment and the buckling of the short beam segment is not relevant. On the other hand, in the case of pinned joint, user sets only normal and shear force and no bending moment but the buckling of the pinned member is relevant so it contributes to the buckling factor. See the figure below. "Model" shows the model in stress-strain analysis type and "Buckling" shows the model in the buckling analysis.

Theoretische achtergrond - Convergeren van de berekening

De eindige-elementenanalyse kan om verschillende redenen niet convergeren, meestal vanwege een element dat niet voldoende wordt ondersteund en vrij kan bewegen of roteren.

Finite element analysis requires slightly increasing stress-strain diagram of material models. In some cases of complicated models, e.g. with multiple contacts, the increase in divergent iterations might help with convergence. This value can be set in Code setup. Most common causes of analysis failure are singularities when the parts of a model are not connected properly and are free to move or rotate. A user is notified and should check the model for missing welds or bolts. The deformed shape is shown with the items which caused the first singularity moved 1 m so that singularity may be easily detected.

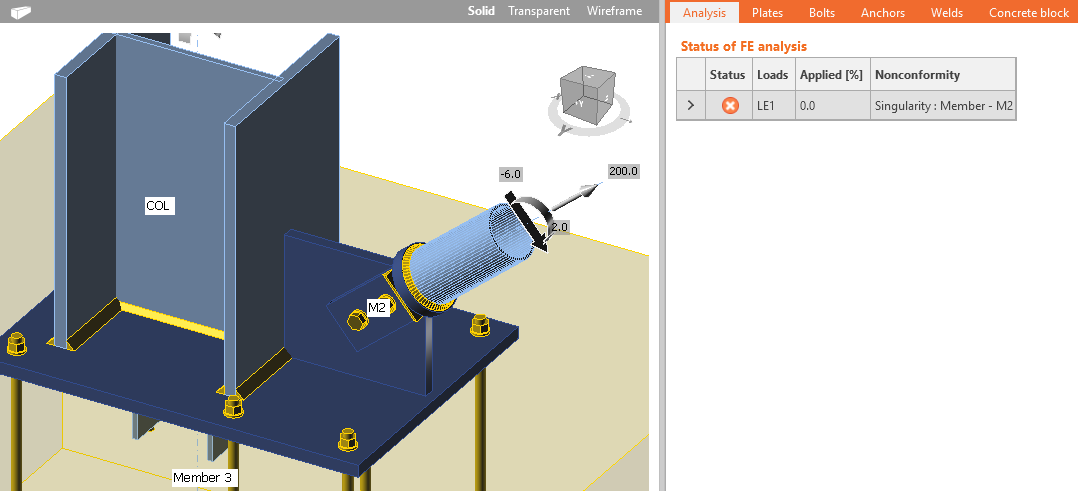
Eindige elementenanalyse vereist een toenemend spannings-rek diagram van materiaalmodellen. In sommige gevallen van complexe modellen, b.v. bij meerdere contacten kan een toename van divergerende iteraties helpen bij de convergentie. Deze waarde kan worden ingesteld in Code-instellingen. De meest voorkomende oorzaken van mislukte berekeningen zijn singulariteiten of instabieliteiten wanneer de onderdelen van een model niet goed zijn aangesloten en vrij kunnen bewegen of roteren. Een gebruiker wordt op de hoogte gebracht en moet het model controleren op ontbrekende lassen of bouten. De vervormde vorm wordt weergegeven met de items die de eerste singulariteit veroorzaakten, zodat singulariteit gemakkelijk kan worden gedetecteerd.

Missende lassen bij een schetsplaat zorgen voor een instabiliteit/onvolkomendheid

Steel-to-timber joints (Theoretical Background)

Steel-to-timber joints are there at the moment only for the check of steel plates and determination of force vectors in fasteners. Gusset plates can be applied as either enclosed or inserted.

The material properties of timber are not specified. The checks of fasteners and the timber should be performed manually or in another software according to appropriate design rules. Therefore, stiffness analysis is not available.

The check of any other components of steel connections are code checked as usual.

Read more about how to work with steel-to-timber joints in the Knowledge base article.

Dunwandige stalen elementen

IDEA StatiCa Connection voor het ontwerpen van verbindingen van dunwandige elementen moet alleen worden overgelaten aan ervaren ingenieurs. Een knikanalyse is een must en elke modusvorm moet zorgvuldig worden geanalyseerd.

De IDEA StatiCa Connection software is bedoeld voor de beoordeling van verbindingen van warmgewalste elementen die niet aanzienlijk worden beïnvloed door knik. De geometrisch lineaire en materieel niet-lineaire analyse wordt uitgevoerd dankzij de snelle en stabiele berekening. Deze analyse is echter niet voldoende voor stabiliteitsverlies. Als knik een probleem kan zijn, helpt het uitvoeren van een lineaire knikanalyse om gevaarlijke gebieden te detecteren en een factor te geven voor het bifurcatiepunt van Euler, maar dit is nog steeds niet voldoende voor dunwandige constructies. Voor dunwandige elementen is alleen een geometrisch niet-lineaire analyse met onvolkomenheden geschikt.

Als de gebruiker toch besluit IDEA StatiCa Connection software te gebruiken om verbindingen van dunwandige elementen te controleren, dan moet hij/zij:

Een lineaire knikanalyse uitvoeren en elke knikvorm zorgvuldig evalueren, de eerste 5 gepresenteerde knikvormen zijn misschien niet genoeg (Hoe kan je het aantal geëvalueerde vormen verhogen)
Niet op de plasticiteit van staalplaten vertrouwen en de von Mises spanning beperken tot de vloeisterkte of zelfs lager.
Ervan bewust zijn dat lokale knik, waarmee geen rekening is gehouden, de interne krachten in onderdelen anders kan verdelen.
Ervan bewust zijn dat de stijfheid van onderdelen anders kan zijn door verschillende faalwijzen of de combinatie daarvan.
Ervan bewust zijn dat de gepresenteerde controles en detaillering van onderdelen (bijv. bouten, lassen) de volgende richtlijnen zijn voor standaardelementen. De controles voor dunwandige elementen kunnen variëren en dan zijn de gegeven controles niet correct.

Het ontwerp van verbindingen van dunwandige elementen is zeer gevalspecifiek en er kan geen algemene richtlijn worden gegeven. IDEA StatiCa Connection is niet gevalideerd voor dit gebruik.

Controle van onderdelen – EN

In EN 1993-1-1 worden dunwandige elementen gedefinieerd als: "Doorsneden van klasse 4 zijn doorsneden waarbij lokale knik optreedt voordat de vloeisterkte in een of meer delen van de doorsnede is bereikt." Het belangrijkste deel van de Eurocode voor staal is beperkt tot elementen met een materiaaldikte van t ≥ 3 mm. Hoofdstuk 4 – Gelaste verbindingen is alleen van toepassing op een materiaaldikte van t ≥ 4 mm. Daarom zijn de controles van onderdelen die door de software worden geleverd niet van toepassing op koudgevormde elementen met een kleinere dikte. Gebruikers moeten zich hiervan bewust zijn en de controles handmatig vervangen door geschikte formules uit EN 1993-1-3.

De analyse van holle doorsnede verbindingen moet ook zorgvuldig worden uitgevoerd voor elementen die buiten het geldigheidsbereik voor lasverbindingen vallen - EN 1993-1-8 - Tabel 7.1. Er bestaan geen richtlijnen voor dergelijke verbindingen en de softwareresultaten zijn niet gevalideerd.

Controle van onderdelen – AISC

In hoofdstuk A van AISC 360-16 staat een opmerking voor de gebruiker: "Voor het ontwerp van koudgevormde stalen constructieve elementen worden de bepalingen in de AISI North American Specification for the Design of Cold-Formed Steel Structural Members (AISI S100) aanbevolen, behalve voor koudgevormde holle constructiedelen (HSS), die volgens deze specificatie worden ontworpen." AISI S100 en AS/NZS 4600 geven formules om de afschuif- en trekweerstand van de meest voorkomende soorten bevestigingen te bepalen, samen met hun toepassingsgebied.

Controle van onderdelen – CISC

CSA S16-14 stelt in Hoofdstuk 1: "Eisen voor stalen constructies zoals bruggen, antennemasten, offshore constructies en koudgevormde stalen constructieve elementen worden gegeven in andere normen van de CSA Group Standards."

Lateral-torsional restraint in structural design

Beams are often restrained against buckling by ceilings or cladding. Simulation of such restriction is provided by manufacturing operation Lateral-torsional restraint (LTR).

Model description

Lateral-torsional restraint is simulated by two stiffnesses added to any plate:

Lateral (shear) S [N] applied in the direction of y axis of plate local coordinate system
Torsional C [Nm/m] applied around x axis of a plate local coordinate system

Users may select any plate of a member, length of the restraint, type (continuous or discrete with set spacing), and lateral and torsional stiffnesses.

Local coordinate system of a plate with applied LTR

Nodes of finite elements are connected along the plate width by rigid body elements type 3 (RBE3) to one point at the plate longitudinal axis. Torsional stiffness is applied at this point by a special element with only one stiffness, rotation around x axis. This point is also connected by two other RBE3 with a special element between them with one stiffness, displacement in y axis.

The lateral stiffness is set by the user as free, rigid, or with set stiffness. Rigid stiffness is sufficiently high, set as 1000 times the shear stiffness of the plate. Stiffness \(S\) is set per unit length (one meter) with a force unit [N]. The stiffness of one element \(S_i\) has a force unit divided by length unit [N/m] and is then:

\[ S_i = \frac{S}{s_d} \]

where:

\(s_d\) – distance between two points [m]

For discrete type, spacing is set directly by the user. For continuous type, the spacing is sufficiently small so that the behavior of the plate is not affected by spacing.

Similarly, the torsional stiffness is set by the user as free, rigid, or with set stiffness. Rigid stiffness is sufficiently high, set as 1 000 times the bending stiffness of the plate. Stiffness \(C\) is set per unit length (one meter) with a unit of bending moment divided by length unit [Nm/m]. The stiffness of one element \(C_i\) has a bending moment unit divided by length unit squared [Nm/m²] and is then:

\[ C_i = \frac{C}{s_d} \]

For a better understanding of the stiffness values, see the document European Recommendations on the Stabilization of Steel Structures by Sandwich Panels.

Hidden finite elements and RBE3 provide lateral and torsional stiffness to member plate

Note that RBE3 are only interpolation links that do not provide any stiffness on their own.

Verification

A model providing LTR was verified by LTBeam software, which uses bar (1D) elements with seven degrees of freedom. That means the cross-section is not deformed, but the element can capture warping. The comparison is shown on an example of IPE 180 cross-section from steel grade S355 with a length of 6 m. The beam is fixed at both ends with a uniform load of 20 kN/m applied at the top flange. Software LTBeam is able to determine the elastic critical moment that corresponds to the result of linear buckling analysis (LBA) in IDEA StatiCa Member.

Comparison of LTBeam and IDEA StatiCa Member for lateral and torsional stiffness

The critical load multiplier to elastic buckling \(\alpha_{cr}\) with lateral stiffness is very similar according to both software. The limit lateral stiffness where lateral-torsional buckling has an effect up to only 5 % of beam bending resistance is calculated according to EN 1993-1-1 as S_lim = 8 589 kN. However, the results with torsional restraint are diverging at higher levels of rotational stiffness. Observing the deformed shape in IDEA StatiCa Member, the difference is caused by the cross-section deformation that can be captured only by the shell model. LTBeam provides unrealistically high critical load multipliers for high torsional stiffness.

To verify this claim, the ABAQUS shell element model was created at ETH university. The beam is again fixed on both ends, made of steel grade S355 and with a length of 6 m. Beam cross-section IPE 240 was used. Limit torsional stiffness, i.e. lateral-torsional buckling has an effect up to only 5 % of beam bending resistance, was calculated as C_lim = 27.13 kNm/m. The model is loaded by force in the mid-span at the top flange.

Comparison of ABAQUS, LTBeam, and IDEA StatiCa Member for torsional stiffness

The effect of torsional stiffness is very similar in both models made of shell elements and LTBeam diverges. Most importantly, ABAQUS and IDEA StatiCa Member buckling resistances provided by GMNIA almost coincide – the differences are up to 4 %.

Stiffness estimation

LTR provided by floors filled with concrete and with composite action provided by shear studs may be assumed as rigid at least in the case of lateral stiffness. The stiffnesses provided by trapezoidal sheets of sandwich panels are much smaller and may be determined by experiments or calculations. Most often, the values of lateral and torsional stiffness would be recommended by manufacturers of sandwich panels or other types of cladding.

The calculation of lateral stiffness S [N] provided by trapezoidal sheets is provided in EN 1993-1-3, Chapter 10:

\[S=1000 \sqrt{t^3} \left ( 50+10 \sqrt[3]{b_{roof}} \right ) \frac{s}{h_w} \]

where:

t – design thickness of trapezoidal sheeting [mm]
b_roof – roof width, i.e. for gable roof it is the distance between a ridge and an eave [mm]
s – distance between beams [mm]
h_w – trapezoidal sheet profile depth [mm]

The formula is valid if the trapezoidal sheet is connected to the beam at each rib. If the sheeting is connected to the beam at every second rib only, then S should be substituted by 0.2 S.

Lateral stiffness of sandwich panels is described in ECCS recommendation. The stiffness of fasteners is essential:

\[S=\frac{k_v}{2B} \sum_{k=1}^{n_k}c_k^2\]

where:

k_v – shear stiffness of a fastening
B – width of a sandwich panel
n_k – number of pairs of fasteners per panel and support
c_k – distance between the two fasteners of a pair

Torsional stiffness is more complicated and can also be estimated by ECCS recommendation. It contains the contribution of fasteners, sandwich panel, and beam distortion. The beam distortion may be neglected because it is already included in the shell element model.

Torsional (on the left) and lateral stiffness (on the right) provided by sandwich panels (ECCS, 2014)

In American practice, restraint against lateral torsional buckling is typically assumed to be full or negligible based on the type and orientation of decking. For example, Table 8.1 of the AISC Seismic Design Manual identifies restraint conditions for beams subject to axial compression. However, where necessary, the lateral stiffness can be derived from the diaphragm stiffness, G’, computed in accordance with AISI S310. Denavit et al. (2020) present a method of calculating torsional stiffness.

References

CTICM, LTBeam v. 1.0.11, available at: https://www.cesdb.com/ltbeam.html
Abaqus. Reference manual, version 6.16. Simulia, Dassault Systéms. France, 2016.
EN 1993-1-3: Eurocode 3: Design of steel structures – Part 1-3: General rules – Supplementary rules for cold-formed members and sheeting, CEN, 2006.
ECCS TC7 – Technical Working Group TWG 7.9 Sandwich Panels and Related Structures, European Recommendations on the Stabilization of Steel Structures by Sandwich Panels, 2^nd edition, 2014. ISBN 978-90-6363-081-2
Denavit, M.D.; Jacobs, W.P.; Helwig, T.A. (2020). "Continuous Bracing Requirements for Constrained-Axis Torsional Buckling," Engineering Journal, American Institute of Steel Construction, Vol. 57, pp. 69-89.

Verbindingen staven met holle doorsnedes

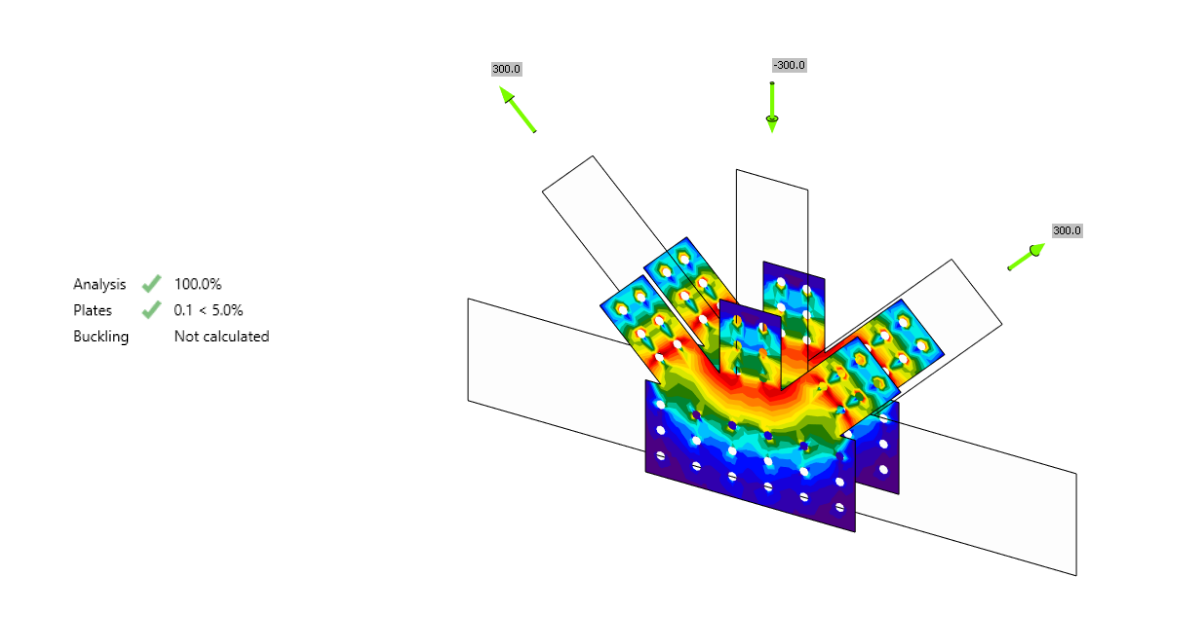
Joints of hollow section members may undergo serious deformations while able to carry still higher loads. On the other hand, the plates may buckle in inelastic range, for which purpose, geometrically and materially nonlinear analysis is implemented.

Verbindingen van holle profielen kunnen ernstige vervormingen ondergaan terwijl ze nog hogere belastingen kunnen dragen. Aan de andere kant kunnen de platen knikken in een niet-elastisch bereik, waarvoor geometrische en materieel niet-lineaire analyse wordt geïmplementeerd.

Uit-het-vlak vervorming

Een van de criteria voor de uiterste grenstoestand van holle profielverbindingen is de uit-het-vlak vervorming van de holle doorsnede. De controle is beschikbaar in de software (in Code Setup als Lokale vervormingscontrole, voor holle doorsnedes standaard ingeschakeld). Het wordt herkend door CIDECT design guides. De limieten zijn 3% van de kleinere afmeting van de doorsnede (0,03 d0 voor CHS en 0,03 b0 voor RHS) voor de uiterste grenstoestand en 1% voor de bruikbaarheidsgrenstoestand.

lokale vervormingen van holle doorsnedes in IDEA CONNECTION

Definitie van doorsnedematen voor ronde buisprofielen (CHS) en rechthoekige kokerprofielen (RHS)

falen van holle dunwandige doorsnedes in IDEA CONNECTION

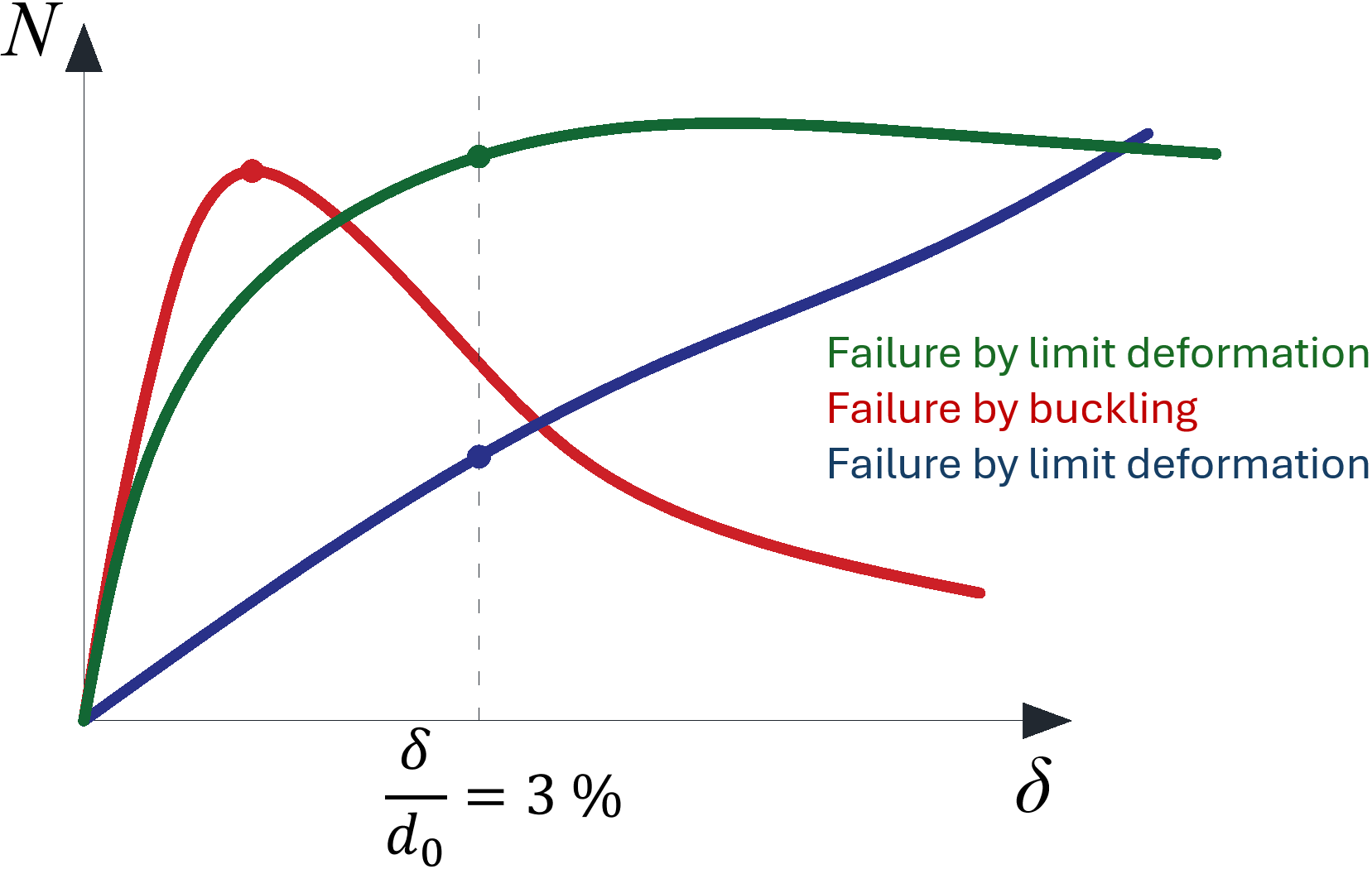
Typical load-deformation diagrams for hollow section joints; the red curve is for thin-walled member loaded in compression, the green curve for regular members loaded in compression, the blue curve is e.g. for X-joint loaded by tension

Typische belastings-vervormingsdiagrammen voor buisprofiel-verbindingen; de rode curve is voor dunwandige staven die op druk worden belast, de groene curve voor normale staven die op druk worden belast, de blauwe curve is b.v. voor X-verbinding belast onder trek.

Geometrisch en materiaal niet-lineare analyse (GMNA)

In het geval van sommige verbindingen van holle profielen, vooral met een hoge diameter / dikte-verhouding, kan de geometrisch lineaire analyse het gedrag van de verbinding niet met voldoende precisie vastleggen en kan de belastingsweerstand worden onderschat of overschat. Het wordt aanbevolen om meer geavanceerde geometrische en materieel niet-lineaire analyse te gebruiken voor verbindingen van holle profielen, ook al is de rekentijd iets hoger. Als GMNA-analyse voor holle profielen is geselecteerd in norm-instellingen, wordt GMNA gebruikt in plaats van geometrisch lineaire en materieel niet-lineaire analyse (MNA, gebruikt als standaard in IDEA Statica Connection) voor modellen met hol profiel als aangesloten staaf

Vermoeiings berekeningstype

Vermoeiingsberekening dient om het normaal- en schuifspanningsbereik tussen twee lasteffecten te bepalen. De spanningen komen overeen met nominale spanningen en moeten verder worden geëvalueerd met behulp van Norm-ontwerpmethoden.

Het moet worden gebruikt voor het ontwerp van hoogcyclische vermoeiingsdetails, waarbij geen vloeien wordt verwacht.

Het type vermoeiingsanalyse biedt geen uiteindelijke weerstand of aantal cycli dat het detail kan nemen. Het levert alleen input voor verdere berekeningen volgens de bedoelde normen.

Er moeten altijd ten minste twee belastinggevallen worden ingesteld. Het eerste belastingsgeval is de referentielast. Het wordt bijvoorbeeld aangenomen als een eigen gewicht van de constructie en kan nullasten bevatten. De andere belastinggevallen simuleren vermoeidheidsacties. De nominale normaal- en schuifspanning geleverd door IDEA StatiCa is het spanningsbereik tussen de vermoeiingsactie, b.v. LE2 en de referentielast.

De schuifspanning op een bepaalde locatie is bijvoorbeeld 50 MPa in het referentielast en 180 MPa in LE2. De weergegeven nominale schuifspanning op deze plaats is:

\[\tau = 180-50=130\, \textrm{MPa}\]

Houd er rekening mee dat platen niet mogen vloeien als gevolg van vermoeiingsacties, anders worden de spanningsbereiken vervormd.

De spanningen zijn beschikbaar voor:

Bouten
Lassen
Platen

Bouten

Bij bouten worden de spanningen eenvoudig bepaald door de kracht te delen door het overeenkomstige gebied:

\(\sigma = F_t / A_s \)
\(\tau = V / A \)

waarbij:

\(F_t\) – trekkracht in de bout
\(A_s\) – trekspanningsgebied van de bout
\(V\) – afschuifkracht in bout; als er meerdere afschuifvlakken zijn, wordt de hoogste afschuifkracht gebruikt
\(A\) – gebied van de bout dat weerstand biedt aan afschuiving

Lassen

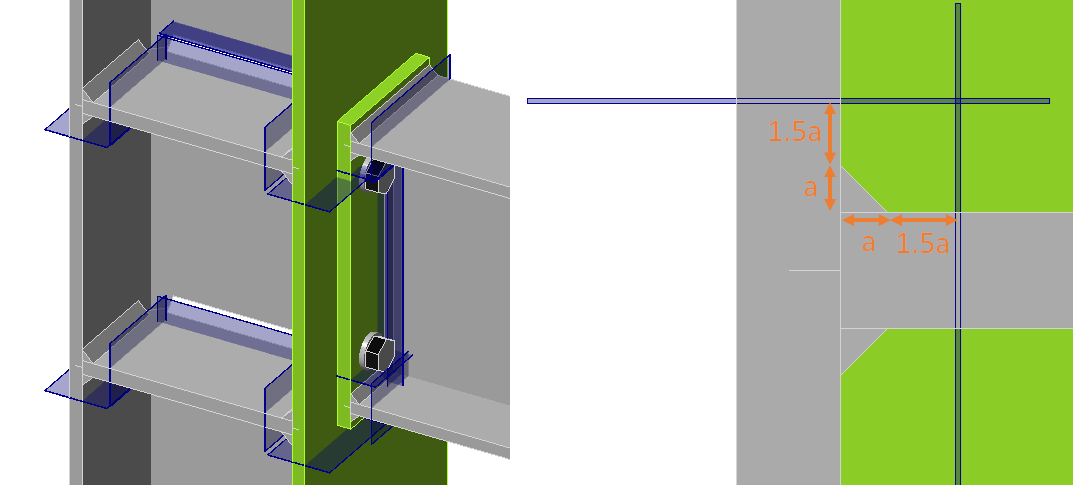
Lassen in CBFEM bestaan uit het laselement met multipoint constraints die de platen verbinden. De spanningsverdeling in de las wordt verstoord door de constraints en daarom worden de spanningen genomen van een sectie die zich op 1,5 keer van de lasgrootte van de las bevindt. Er worden drie secties gemaakt voor een dubbelzijdige hoeklas. Twee secties vallen in dezelfde detailcategorie en alleen de meer benadrukte wordt getoond. De maximale normaalspanning en de bijbehorende schuifspanning op dezelfde locatie, evenals de maximale schuifspanning en de bijbehorende normaalspanning op dezelfde locatie worden weergegeven.

Vermoeiingsberekening van de las in IDEA CONNECTION

Platen

The stress in plates may be visualized by creating a user-defined section by a Workplane manufacturing operation. In the figure below, two workplanes were created to see the stresses around bolt holes. The maximum normal stress and the corresponding shear stress at the same location, as well as the maximum shear stress and the corresponding normal stress at the same location are shown.

De spanning in platen kan worden gevisualiseerd door een door de gebruiker gedefinieerde sectie te maken door een Workplane-bewerking. In de onderstaande afbeelding zijn twee werkvlakken gemaakt om de spanningen rond boutgaten te kunnen zien. De maximale normaalspanning en de bijbehorende schuifspanning op dezelfde locatie, evenals de maximale schuifspanning en de bijbehorende normaalspanning op dezelfde locatie worden weergegeven.

Fire design

Fire design is available for user-set temperatures. Reduced material characteristics are used based on preset temperature and material degradation curve. Fire design is available in Connection and Member applications.

Temperature

In IDEA StatiCa Member, the user sets a temperature for the whole model. All entities in the model have a set temperature.

In IDEA StatiCa Connection, the user may set the temperature for each member or plate separately. The temperature of connecting elements - bolts and welds - is assumed to be according to the hottest connecting plate.

The temperature of members and plates in connections may be determined according to EN 1993-1-2 – Cl. 4.2.5 Steel temperature development and D.3 Temperature of joints in fire.

Material degradation

Material degradation of steel plates is available according to three codes:

EN 1993-1-2 – Table 3.1
AISC 360-16 – Table A-4.2.1
CSA S16-14 – Table K.1

The multilinear material diagram is used for steel plates with six points according to EN 1993-1-2 – Figure 3.1. An example is shown for steel grade S355, material degradation according to EN 1993-1-2 – Table 3.1, and temperature \(\theta = 560^{\circ}\textrm{C}\). The slope of plastic branch past the yield strength \(f_y\) is \(E_{a,\theta}/1000\). The reduction factors for modulus of elasticity \(k_{E,\theta}\), for proportionality limit \(k_{p,\theta}\), and yield strength \(k_{y,\theta}\) are 0.426, 0.252, and 0.594, respectively. The plastic strain is assumed to build up since the proportionality limit.

	Strain	Plastic strain	Stress
	\(\varepsilon\) [%]	\(\varepsilon_{pl}\) [%]	\(\sigma\) [MPa]
0	0.00	0.00	0.0
1	0.10	0.00	89.5
2	0.25	0.15	131.4
3	0.50	0.40	160.5
4	1.00	0.90	191.3
5	2.00	1.90	210.9
6	15.00	14.90	222.5

Material degradation of bolts is available according to three codes:

EN 1993-1-2 – Table D.1
AISC 360-16 – Table A-4.2.3
CSA S16-14 – Table K.3

Material degradation of welds is available according to one code:

EN 1993-1-2 – Table D.1

Only the resistance of bolts and welds is reduced. Their stiffness remains the same as at ambient temperature.

Thermal expansion is neglected and not assumed in any models. If necessary, the effects of thermal expansion should be simulated by added loads.

Checks

Steel plates are checked for plastic strain 5% by default.

In Eurocode, a dedicated partial safety factor for Fire design, \(\gamma_{M,fi}\) is used for checks of bolts and welds. In all other codes, the standard resistance or safety factors are used. The load-deformation curves and checks of bolts and welds are reduced by factors \(k_b\) and \(k_f\) based on set temperature.

Preloaded bolts are assumed to slip and are checked as regular snug-tight bolts.

The temperature of the concrete block and anchors is unknown and corresponding components are not checked in Fire design.

Stiffness

Stiffness analysis is not available for Fire design at the moment. It is recommended to use stiffness analysis for ambient temperature and multiply the stiffness by reduction factor for modulus of elasticity \(k_{E,\theta}\).

IDEA StatiCa Connection – Structural design of steel connections

Introduction to the CBFEM method

Analysis model of IDEA StatiCa

Specifications for national codes

Introduction to CBFEM method

Algemene inleiding voor het constructief ontwerp van staalverbindingen

Inleiding

Componentenmethode

Wil je je vaardigheden verbeteren? Bezoek onze campus

Materiaal model

Plaatmodel en netconvergentie

Plaatmodel

Netconvergentie

Contacten tussen stalen verbindingsplaten

Lassen

Plastische herverdeling van spanningen in lassen

Bolts and preloaded bolts connections

Bolts

Bolt in tension

Bolt in shear

Interaction between tension and shear

Preloaded bolts

Ankerbouten

Ankerbouten met stand-off

Betonblok

Ontwerpmodel

Vervormingsstijfheid

Overdracht van afschuifbelasting op de grondplaat

Overdracht van afschuifbelasting door wrijving

Overdracht van afschuifbelasting door kluft

Overdracht van afschuifbelasting door ankers

Analysis model of IDEA StatiCa

Rekenmodel voor staalverbindingen

Dragende elementen en ondersteuningen

Knoopevenwicht in het 3D FEM-model

Loads

Import loads from FEA programs

Sterkteanalyse van staalverbindingen

Stijfheidsberekening en vervormingscapaciteit

Vervormings capaciteit

Weerstandsberekening van staalverbindingen

Weerstand van de verbinding

Buckling analysis

Theoretische achtergrond - Convergeren van de berekening

Steel-to-timber joints (Theoretical Background)

Dunwandige stalen elementen

Controle van onderdelen – EN

Controle van onderdelen – AISC

Controle van onderdelen – CISC

Lateral-torsional restraint in structural design

Model description

Verification

Stiffness estimation

References

Verbindingen staven met holle doorsnedes

Uit-het-vlak vervorming

Geometrisch en materiaal niet-lineare analyse (GMNA)

Vermoeiings berekeningstype

Bouten

Lassen

Platen

Fire design

Temperature

Material degradation

Checks

Stiffness

Gerelateerde artikelen

Check of steel connection components (AISC)

Controle van componenten volgens de Eurocode

Check of steel connection components (CSA)

Check of steel connection components (GB)

Check of steel connection components (AS)

Check of steel connection components (HKG)

Check of steel connection components (IS 800)

Check of steel connection components (SP)