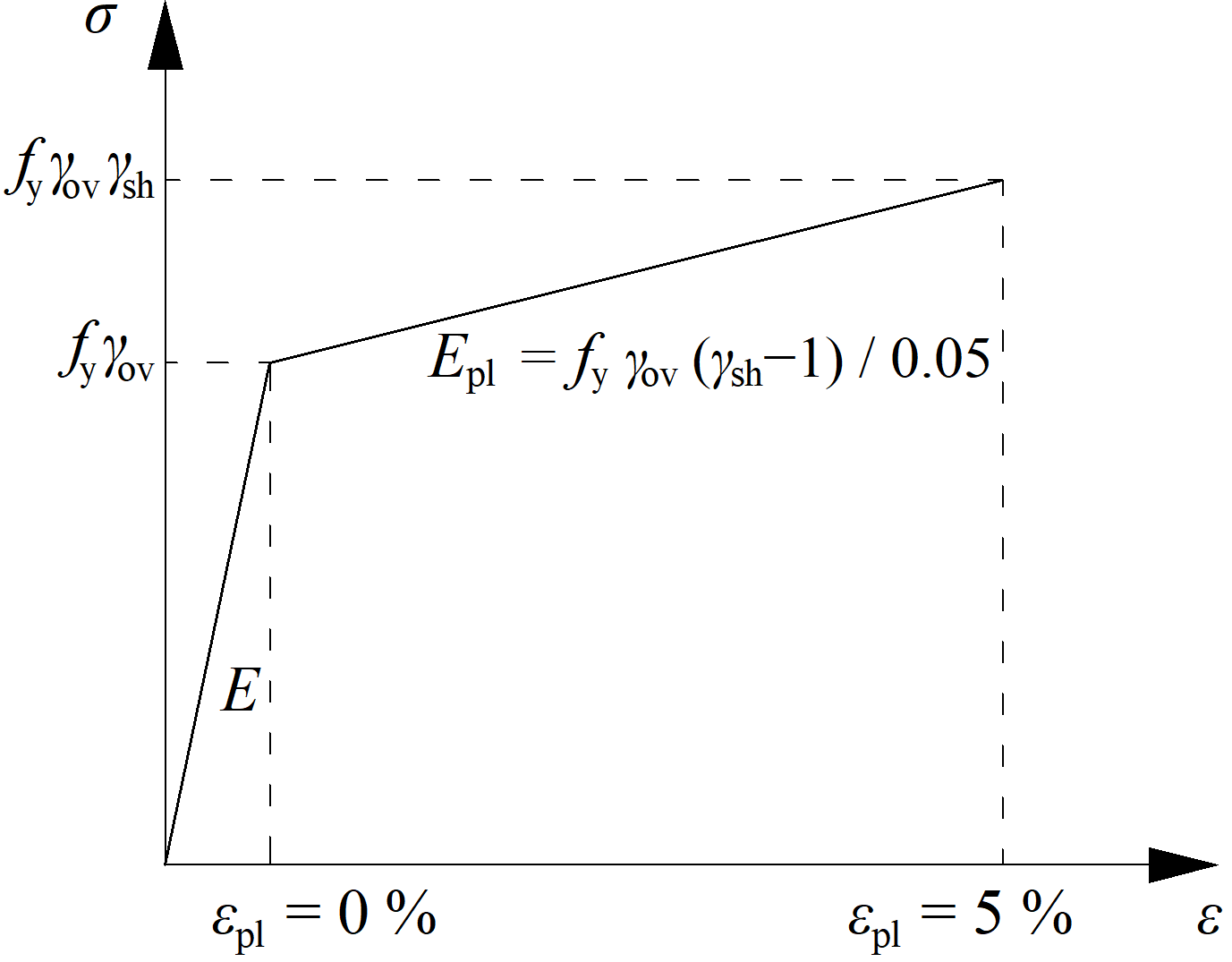IDEA StatiCa Connection - Progettazione strutturale delle connessioni in acciaio

Introduzione al metodo CBFEM

Introduzione generale alla progettazione strutturale delle connessioni in acciaio
Modello del materiale del collegamento in acciaio
Modello della piastra e convergenza della mesh
Contatti tra le piastre di connessioni in acciaio
Analisi delle connessioni saldate
Connessioni con bulloni e bulloni precaricati
Bulloni di ancoraggio
Modello strutturale di un blocco di calcestruzzo

Modello di analisi di IDEA StatiCa

Modello di analisi dei giunti in acciaio
Equilibrio del nodo nel modello FEM 3D
Forze interne nelle connessioni in acciaio
Analisi della resistenza dei giunti in acciaio
Analisi della rigidezza e della capacità di deformazione dei giunti in acciaio
Progettazione in capacità della connessione in acciaio
Resistenza di progetto della connessione in acciaio
Analisi di instabilità dei giunti in acciaio
Convergenza dell'analisi di modelli complessi di connessioni in acciaio
Giunti acciaio-legno
Membrature in acciaio a parete sottile
Vincolo latero-torsionale nella progettazione strutturale
Giunti in acciaio di membrature a sezione cava
Analisi a fatica nella progettazione strutturale
Progettazione in caso di incendio
Dimensionamento delle saldature

Specifiche per i codici nazionali

Verifica delle componenti in accordo a EN (Eurocodice)
Verifica delle componenti in accordo a AISC (American standards)
Verifica delle componenti in accordo a CISC (Canadian standards)
Verifica delle componenti in accordo a AS (Australian standards)
Verifica delle componenti in accordo a SP (Russian standards)
Verifica delle componenti in accordo a IS 800 (Indian standards)
Verifica delle componenti in accordo a HKG (Hong Kong Code of Practice)
Verifica delle componenti in accordo a GB (Chinese standards)

Introduzione al metodo CBFEM

Introduzione generale alla progettazione strutturale delle connessioni in acciaio

Introduzione

Nella progettazione di strutture in acciaio, gli ingegneri preferiscono l’utilizzo di membrature ad asta. Tuttavia, ci sono molti punti della struttura in cui la teoria delle membrature non è valida, ad esempio i giunti saldati, le connessioni bullonate, i piedritti, i fori nelle pareti, la rastrematura della sezione e i carichi concentrati. L'analisi strutturale in questi punti è complessa e richiede un'attenzione particolare. Il comportamento è non lineare e le non linearità devono essere rispettate, ad esempio la resistenza limite del materiale delle piastre, il contatto tra le piastre di estremità o la piastra di base e il blocco di calcestruzzo, le azioni unilaterali di bulloni e ancoraggi, le saldature. I codici di progetto, ad esempio EN1993-1-8, e la letteratura tecnica offrono metodi di soluzione ingegneristica. La loro caratteristica generale è la derivazione per forme strutturali tipiche e carichi semplici. Un metodo utilizzato molto spesso è quello delle componenti.

Metodo delle Componenti

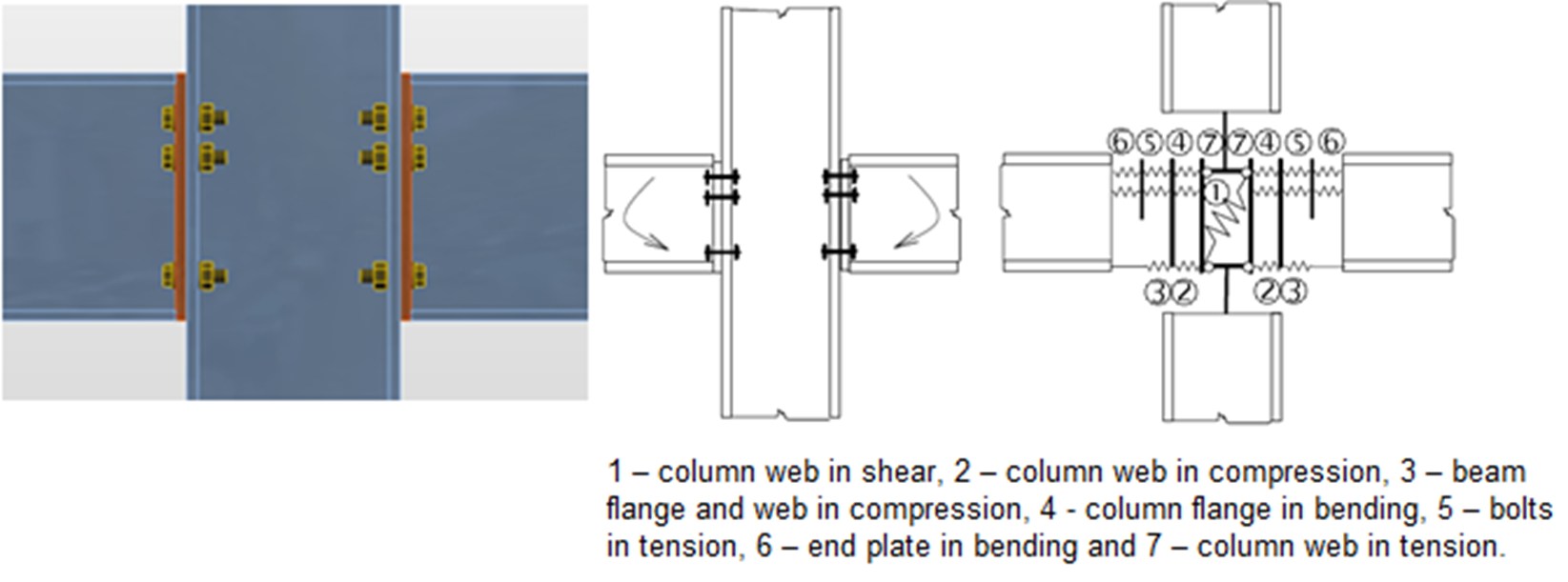
Il metodo delle componenti (MC) risolve il giunto come un sistema di elementi interconnessi: le componenti. Per ogni tipo di giunto viene costruito il modello corrispondente per poter determinare le forze e le sollecitazioni in ogni componente. Si veda la figura seguente.

Componenti di un giunto con piastre di estremità bullonate modellate da molle

Ogni componente è verificato separatamente utilizzando le formule corrispondenti. Poiché per ogni tipo di giunto deve essere creato il modello appropriato, l'utilizzo del metodo presenta dei limiti nella risoluzione di giunti di forma generica e con carichi generici.

IDEA StatiCa, insieme a un team di progetto del Dipartimento di Strutture in acciaio e legno della Facoltà di Ingegneria Civile di Praga e dell'Istituto di Strutture in metallo e legno della Facoltà di Ingegneria Civile dell'Università Tecnologica di Brno, ha sviluppato un metodo per la progettazione avanzata di giunti strutturali in acciaio.

Il Modello agli Elementi Finiti Basato sulle Componenti (Component Based Finite Element Model - CBFEM) è:

• Generale al punto da poter essere utilizzato per la maggior parte dei giunti, collegamenti a terra e dettagli nella pratica ingegneristica.
• Semplice e veloce nella pratica quotidiana, al punto da fornire risultati in tempi paragonabili ai metodi e agli strumenti attuali.
• Completo al punto da fornire all'ingegnere strutturale informazioni chiare sul comportamento, le sollecitazioni e le deformazioni dei giunti, e sulle riserve delle singoli componenti nonché sulla sicurezza e affidabilità complessive.

Il metodo CBFEM si basa sull'idea di tenere valide la maggior parte delle parti verificate e molto utili del MC. Il punto debole del MC, ossia la sua generalità nell'analisi delle sollecitazioni dei singoli componenti, è stato sostituito dalla modellazione e dall'analisi con il metodo degli elementi finiti (FEM).

Il FEM è un metodo generale comunemente utilizzato per l'analisi strutturale. L'uso del FEM per la modellazione di giunti di qualsiasi forma risulta ideale (Virdi, 1999). È necessaria l'analisi elastoplastica poiché l'acciaio normalmente si snerva nella struttura. In effetti, i risultati dell'analisi lineare non sono utili al fine della progettazione dei giunti.

I modelli FEM sono utilizzati per scopi di ricerca sul comportamento dei giunti, e applicano solitamente elementi spaziali e valori misurati delle proprietà dei materiali.

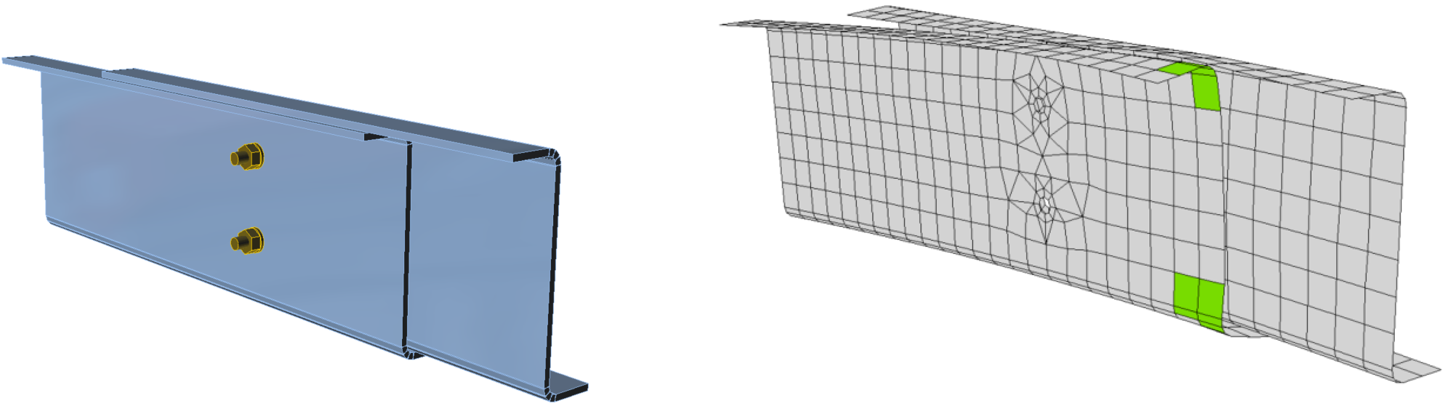
Modello FEM di un giunto a scopo di ricerca. Si avvale di elementi spaziali 3D sia per le piastre che per i bulloni

Sia le anime che le ali degli elementi collegati sono modellate con l’uso di elementi shell nel modello CBFEM, per il quale è disponibile una soluzione nota e verificata.

Gli elementi di fissaggio, ossia bulloni e saldature, sono i più difficili dal punto di vista del modello di analisi. La modellazione di tali elementi nei programmi FEM generali è difficile perché i programmi non offrono le proprietà richieste. Pertanto, è stato necessario sviluppare componenti FEM speciali per modellare il comportamento delle saldature e dei bulloni in un giunto.

Modello CBFEM di connessione con piastra con piastra bullonata

Nell’analisi di strutture a telaio o a trave primaria in acciaio, i giunti delle membrature sono modellati come punti senza massa. Le equazioni di equilibrio vengono assemblate nei giunti e le forze interne alle estremità delle travi vengono determinate dopo aver risolto l'intera struttura. Infatti, il giunto è caricato da queste forze. La risultante delle forze di tutte le membrature del giunto è pari a zero: l'intero giunto è in equilibrio.

La forma reale di un giunto non è nota nel modello strutturale. L'ingegnere definisce solo se il giunto sia rigido o sia una cerniera.

È necessario creare un modello affidabile di giunto, che rispetti lo stato reale, per progettare il giunto in modo corretto. Nel metodo CBFEM si utilizzano le estremità delle membrature con lunghezza pari a un multiplo di 2-3 dell'altezza massima della sezione. Questi segmenti sono modellati con elementi shell.

Un giunto teorico (senza massa) e la forma reale del giunto senza le estremità modificate della membratura

Per una maggiore precisione del modello CBFEM, le forze di estremità sulle membrature 1D sono applicate come carichi alle estremità dei segmenti. Le sestine di forze del giunto teorico vengono trasferite all'estremità del segmento; i valori delle forze vengono mantenuti, ma i momenti vengono modificati dalle azioni delle forze sui bracci corrispondenti.

Le estremità dei segmenti in corrispondenza del giunto non sono collegate. La connessione deve essere modellata. Il metodo CBFEM si avvale delle cosiddette operazioni di produzione per modellare la connessione. Le operazioni di produzione sono in particolare: tagli, offset, fori, rinforzi, nervature, piastre di estremità e piatti di giunzione, coprigiunti, fazzoletti e altro. Vengono inoltre aggiunti elementi di fissaggio (saldature e bulloni).

IDEA StatiCa Connection può eseguire due tipi di analisi:

1. Analisi lineare per geometria con non linearità del materiale e di contatto per l'analisi delle tensioni e delle deformazioni,
2. Analisi degli autovalori per determinare la possibilità di instabilità.

Nel caso delle connessioni, l'analisi non lineare per geometria non è necessaria, a meno che le piastre non siano molto sottili. La snellezza della piastra può essere determinata dall'analisi degli autovalori (instabilità). Per la snellezza limite in cui l'analisi lineare per geometria è ancora sufficiente, si veda il Capitolo 3.9. L'analisi non lineare per geometria non è implementata nel software.

Modello del materiale del collegamento in acciaio

I diagrammi dei materiali più comuni che vengono utilizzati nella modellazione ad elementi finiti dell'acciaio strutturale sono il modello plastico o elastico ideale con incrudimento e il vero diagramma sforzo-deformazione. Il vero diagramma sforzo-deformazione è calcolato dalle proprietà dei materiali degli acciai dolci a temperatura ambiente ottenute nelle prove di trazione. La tensione e la deformazione reali possono essere ottenute come segue:

\[ \sigma_{true}=\sigma (1 + \varepsilon) \]

\[ \varepsilon_{true}=\ln (1 + \varepsilon) \]

dove σ_true è la tensione reale, ε_true la deformazione reale, σ la tensione ingegneristica, e ε la deformazione ingegneristica.

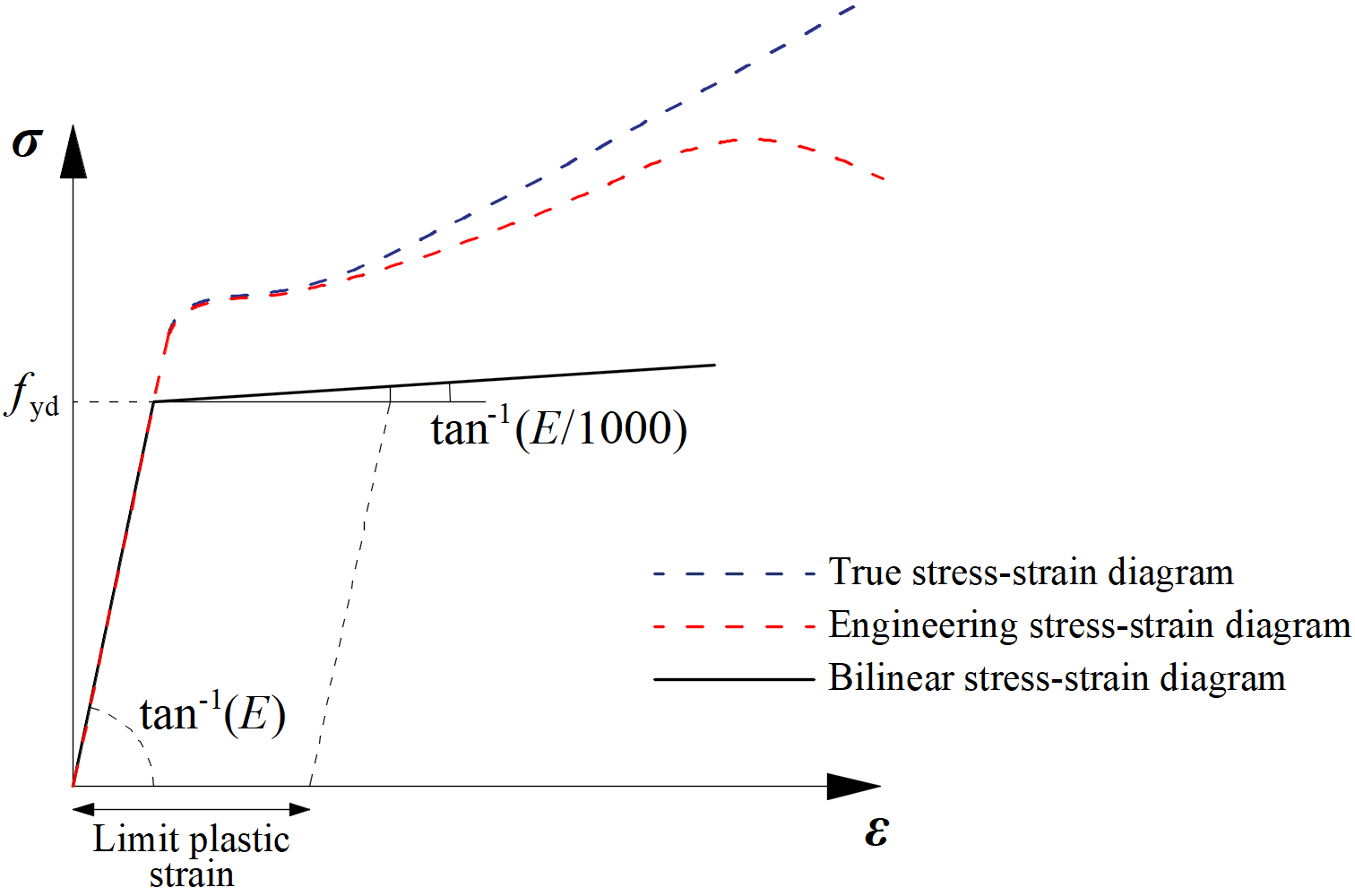
Le piastre in  IDEA StatiCa Connection sono modellate con materiale elastico perfettamente plastico con incrudimento lineare indicato nell’EN 1993-1-5, app. C, par. C6, (2) modello b). Il comportamento del materiale si basa sul criterio di snervamento di von Mises. Si presume che sia elastico prima di raggiungere il carico di snervamento di progetto, f_yd.

Il criterio dello stato limite ultimo per le regioni non suscettibili a  buckling è il raggiungimento del valore limite della deformazione della membrana principale. Si consiglia il valore del 5% (ad esempio EN1993-1-5, App. C, Par. C.8, Nota 1).

Diagrammi dei materiali dell'acciaio nei modelli numerici

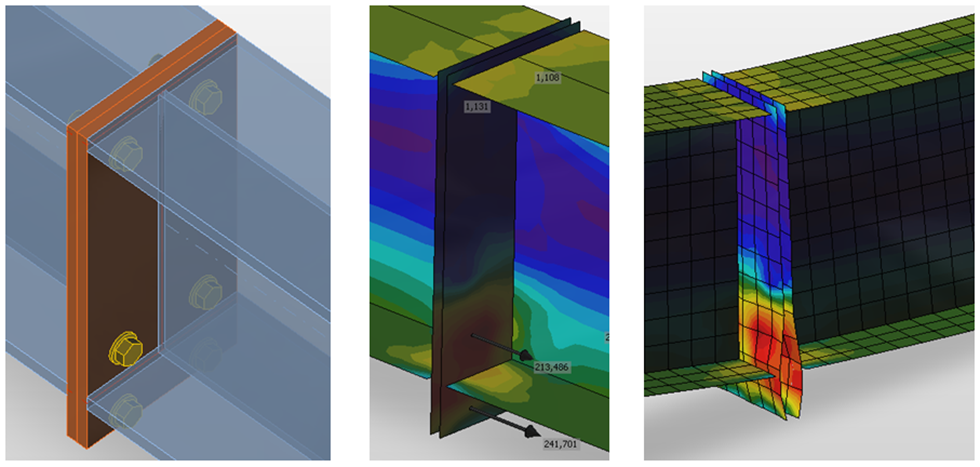
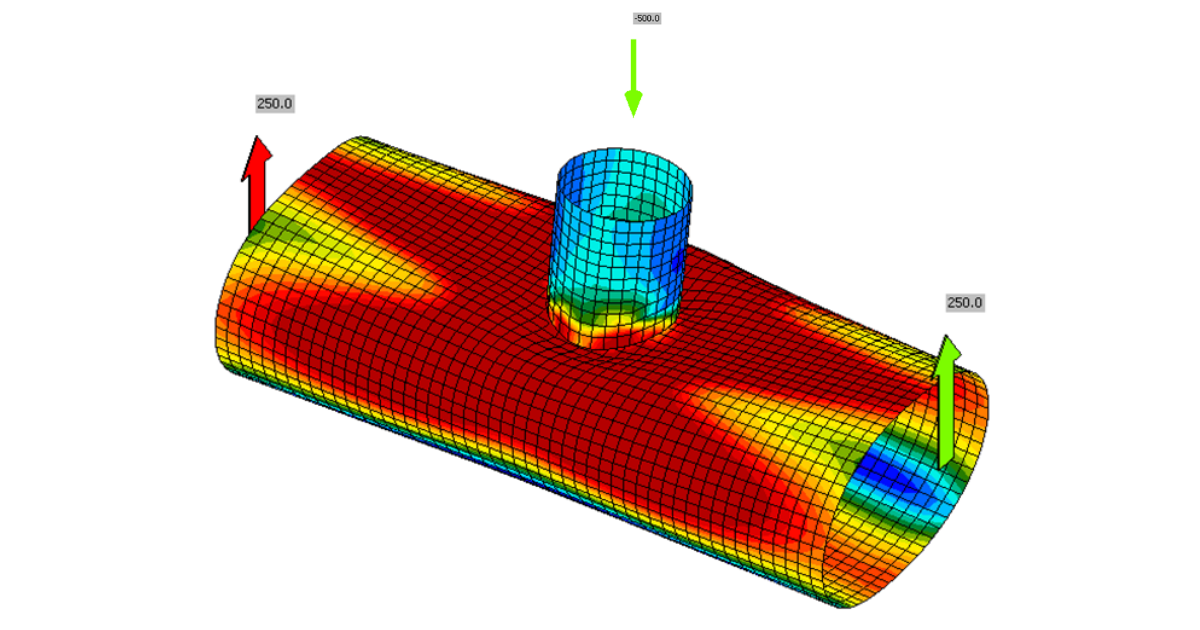
Il valore limite della deformazione plastica viene spesso discusso. Infatti, il carico ultimo ha una bassa sensibilità al valore limite della deformazione plastica quando viene utilizzato il modello plastico ideale. Ciò è dimostrato nel seguente esempio di un giunto trave-colonna. Una trave a sezione aperta IPE 180 è collegata ad una colonna a sezione aperta HEB 300 e caricata dal momento flettente. L'influenza del valore limite della deformazione plastica sulla resistenza della trave è mostrata nella figura seguente. La deformazione plastica limite varia dal 2 % all'8 %, ma la variazione del momento resistente è inferiore al 4 %.

Un esempio di previsione dello stato limite ultimo di un giunto trave-pilastro

L'influenza del valore limite della deformazione plastica sul momento resistente

Modello della piastra e convergenza della mesh

L'aumento del numero di elementi fornisce risultati più precisi, ma al costo di una maggiore richiesta di calcolo.

Modello della piastra

Si consigliano gli elementi shell per la modellazione delle piastre nella FEA delle connessioni strutturali. Si applicano elementi shell quadrangolari a 4 nodi con nodi agli angoli. Per ogni nodo si considerano sei gradi di libertà: 3 traslazioni(u_x, u_y, u_z) e 3 rotazioni(φ_x, φ_y, φ_z). Le deformazioni dell'elemento sono suddivise in componenti membranale e flessionale.

La formulazione del comportamento membranale si basa sul lavoro di Ibrahimbegovic (1990). Si considerano le rotazioni perpendicolari al piano dell'elemento. Viene fornita una formulazione in 3D completa dell'elemento. Le deformazioni a taglio fuori piano sono considerate nella formulazione del comportamento flessionale di un elemento sulla base dell’ipotesi di Mindlin. Viene applicata la nostra variante stabilizzata dell’elemento piastra quadratico di Mindlin con deformazione a taglio costante lungo il bordo. Gli elementi sono ispirati agli elementi MITC4; si veda Dvorkin (1984). La membrana (shell) è suddivisa in cinque strati di integrazione nello spessore della piastra, in ogni punto di integrazione, e viene analizzato il comportamento plastico in ogni punto. Si chiama integrazione di Gauss-Lobatto. La fase elastoplastica non lineare del materiale viene analizzata in ogni strato sulla base delle deformazioni note. Vengono mostrate solo le sollecitazioni e le deformazioni massime di tutti gli strati.

Convergenza della mesh

Esistono alcuni criteri per la creazione della mesh nel modello della connessione. La verifica della connessione deve essere indipendente dalla dimensione dell'elemento. La creazione della mesh su una piastra separata non presenta problemi. Occorre prestare attenzione alle geometrie complesse, come i pannelli irrigiditi, i T-stubs e le piastre di base. Per geometrie complicate, deve essere eseguita l'analisi di sensibilità che considera la discretizzazione della mesh.

Tutte le piastre della sezione sezione di una trave hanno una divisione comune in elementi. La dimensione degli elementi finiti generati è limitata. La dimensione minima dell'elemento è impostata su 10 mm e la dimensione massima dell'elemento su 50 mm (può essere impostata nella finestra Impostazione codice). Le mesh delle ali e delle anime sono indipendenti gli une dalle altre Il numero predefinito di elementi finiti è impostato su 8 elementi per altezza della sezione, come mostrato nella figura seguente. L'utente può modificare i valori predefiniti nella finestra Impostazione codice.

Mesh di una trave con vincoli tra le piastre d'ala e d'anima

La mesh delle piastre di estremità è separata e indipendente dalle altre parti della connessione. La dimensione predefinita degli elementi finiti è impostata su 16 elementi per altezza della sezione, come mostrato in figura.

La mesh su una piastra di estremità con 7 elementi lungo la sua larghezza

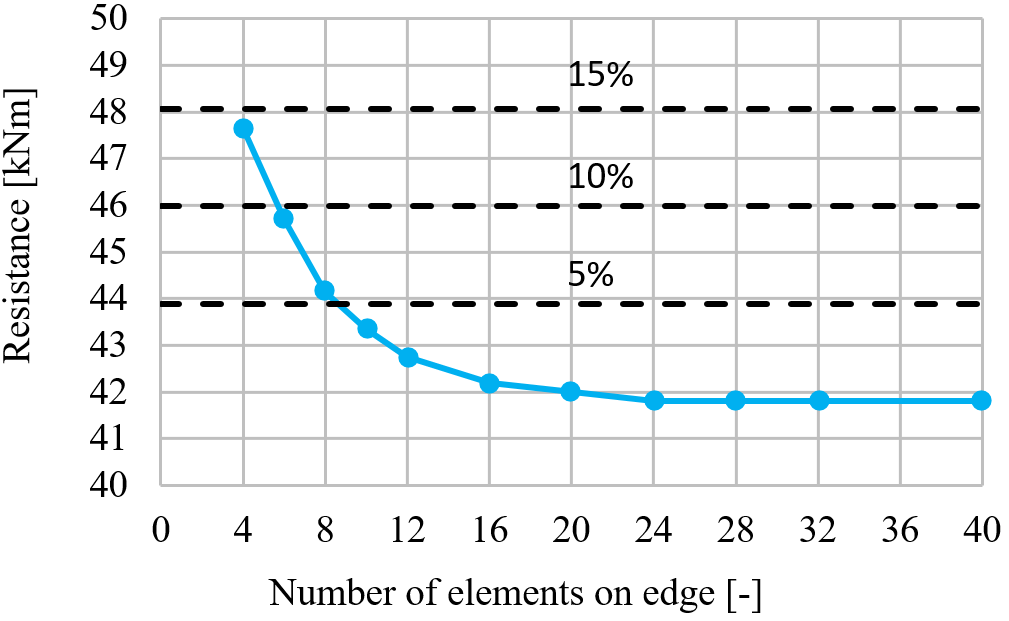
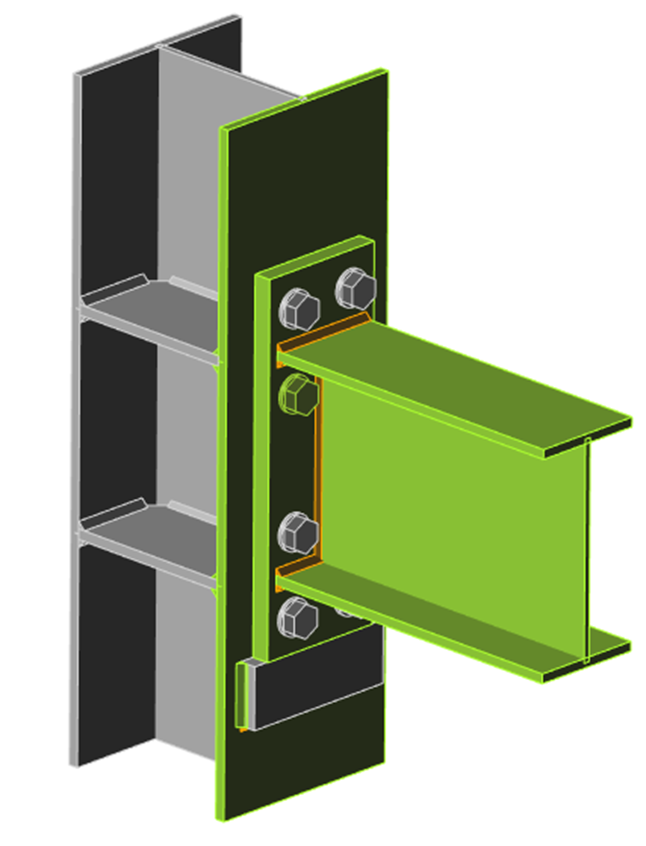
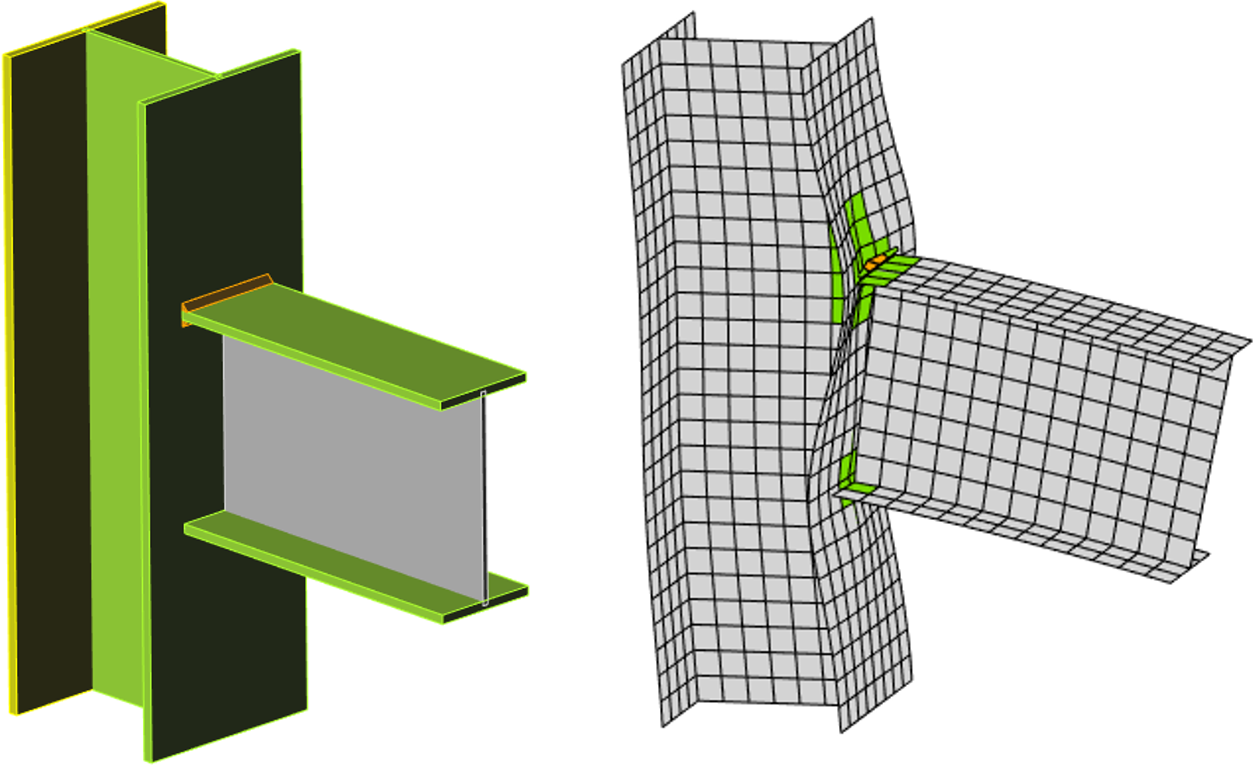
L'esempio seguente di un giunto trave-pilastro mostra l'influenza della dimensione della mesh sulla resistenza al momento. Una trave a sezione aperta IPE 220 è collegata a un pilastro a sezione aperta HEA 200 e caricata da un momento flettente come mostrato nella figura seguente. La componente critica è il pannello del pilastro a taglio. Il numero di elementi finiti lungo l'altezza della sezione trasversale varia da 4 a 40 e i risultati vengono confrontati. Le linee tratteggiate rappresentano le differenze del 5%, 10% e 15%. Si consiglia di suddividere l'altezza della sezione in 8 elementi.

Modello di giunto trave-pilastro e deformazioni plastiche allo stato limite ultimo

Influenza del numero di elementi sulla resistenza al momento

Viene presentato lo studio di sensibilità della mesh di un irrigidimento compresso e sottile di un pannello d’anima di un pilastro. Il numero di elementi lungo la larghezza dell'irrigidimento varia da 4 a 20. La figura seguente mostra la prima modalità di instabilità e l'influenza di un certo numero di elementi sulla resistenza all'instabilità e sul carico critico. Viene visualizzata la differenza del 5% e del 10%. Si consiglia di utilizzare 8 elementi lungo la larghezza dell'irrigidimento.

Prima modo di buckling e influenza del numero di elementi lungo l'irrigidimento sulla resistenza al momento

Viene presentato lo studio di sensibilità della mesh di un T-stub soggetto a trazione. La metà della larghezza della flangia è suddivisa da 8 a 40 elementi e la dimensione minima dell'elemento è impostata a 1 mm. L'influenza del numero di elementi sulla resistenza del T-stub è mostrata nella figura seguente. Le linee tratteggiate rappresentano la differenza del 5%, 10% e 15%. Si consiglia di utilizzare 16 elementi sulla metà della larghezza dell'ala.

Influenza del numero di elementi sulla resistenza del T-stub

Contatti tra le piastre di connessioni in acciaio

Per la modellazione del contatto tra piastre si raccomanda il metodo di penalità standard. Se viene rilevata la penetrazione di un nodo in una superficie di contatto opposta, viene aggiunta una rigidezza di penalità tra il nodo e la piastra opposta. La rigidezza di penalità è controllata da un algoritmo euristico durante l'iterazione non lineare per ottenere una migliore convergenza. Il solutore rileva automaticamente il punto di penetrazione e risolve la distribuzione della forza di contatto tra il nodo in penetrazione e i nodi della piastra opposta. Permette di creare contatti tra diverse mesh, come mostrato. Il vantaggio del metodo di penalità è l'assemblaggio automatico del modello. Il contatto tra piastre ha un impatto importante sulla ridistribuzione delle forze nella connessione.

Esempio di separazione di piastre a contatto tra l'anima e le ali di due arcarecci con sezione a Z sovrapposti

È possibile aggiungere un contatto tra

• due superfici,
• due bordi,
• bordo e superficie.

Esempio di contatto tra bordi tra la piastra inferiore e la piastra di estremità

Esempio di contatto bordo-superficie tra l'ala inferiore della trave e l'ala del pilastro

È possibile visualizzare le tensioni di contatto, i valori sono riportati nella tabella della verifica delle piastre. Tuttavia, le tensioni di contatto sono solo informative e non vengono utilizzate in alcuna verifica. Inoltre, la tensione attraverso lo spessore delle piastre dell'elemento shell non è considerata. 

Analisi delle connessioni saldate

Esistono diverse opzioni per la gestione delle saldature nei modelli numerici. Le grandi deformazioni rendono l'analisi meccanica più complessa ed è possibile utilizzare diverse descrizioni di mesh, diverse variabili cinetiche e cinematiche e modelli costitutivi. In genere si utilizzano diversi tipi di modelli geometrici 2D e 3D e quindi elementi finiti con la loro applicabilità a diversi livelli di accuratezza. Il modello del materiale più utilizzato è il comune modello di plasticità indipendente dalla velocità, basato sul criterio di snervamento di von Mises. Si descrivono due approcci utilizzati per le saldature. Le sollecitazioni residue e le deformazioni causate dalla saldatura non sono considerate nel modello di progetto.

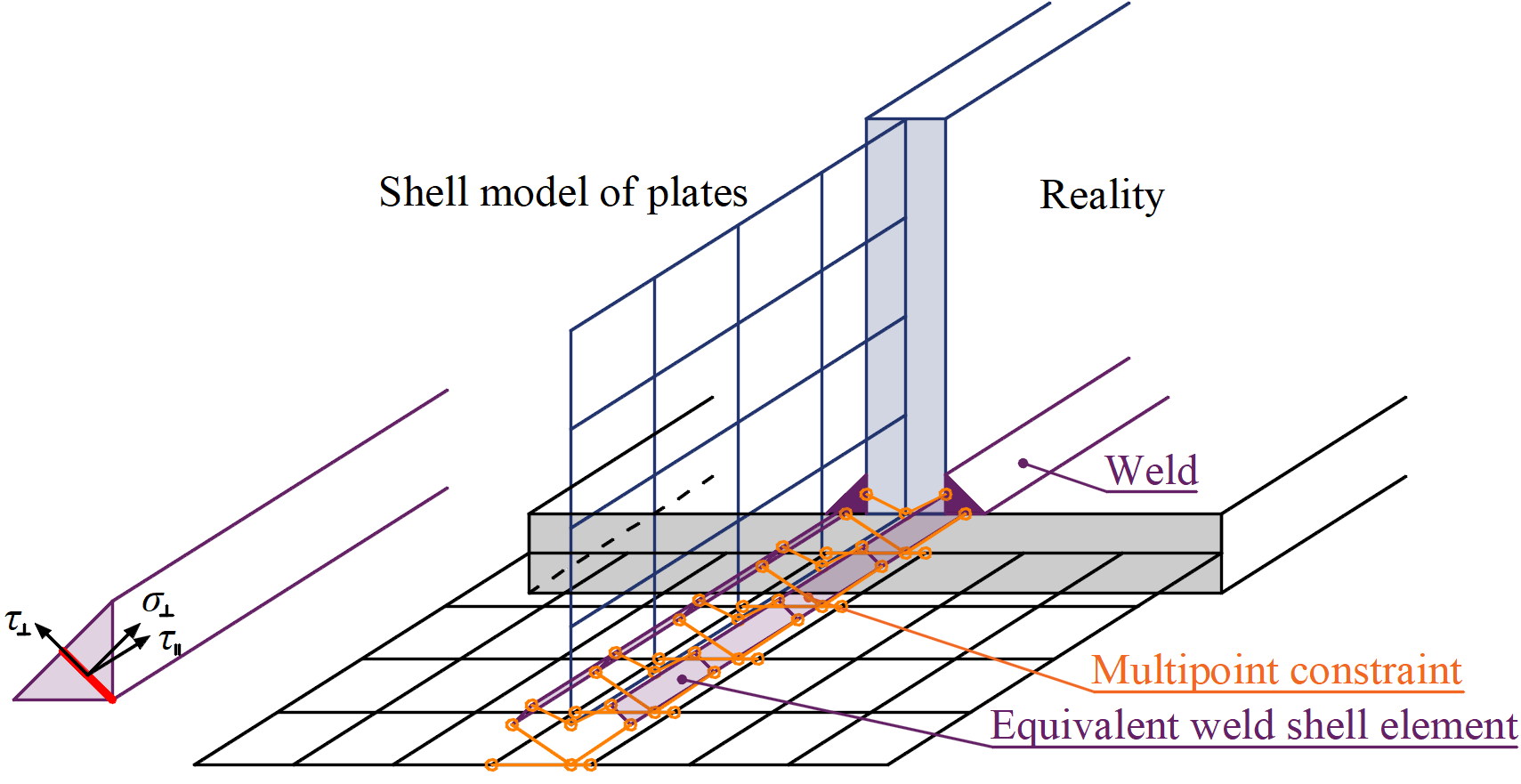
Il carico viene trasmesso alla piastra opposta attraverso vincoli di forza-deformazione basati sulla formulazione Lagrangiana. La connessione è chiamata vincolo multipunto (MPC) e mette in relazione i nodi degli elementi finiti di un bordo della piastra con un altro. I nodi degli elementi finiti non sono collegati direttamente. Il vantaggio di questo approccio è la possibilità di collegare mesh con densità diverse. Il vincolo consente di modellare la superficie della linea mediana delle piastre collegate con l'offset, che rispetta la configurazione reale della saldatura e lo spessore di gola. La distribuzione del carico nella saldatura è derivata dall'MPC, quindi le sollecitazioni sono calcolate nella sezione della gola. Ciò è importante per la distribuzione delle sollecitazioni nella piastra sotto la saldatura e per la modellazione dei T-stubs.

Ridistribuzione delle sollecitazioni plastiche nelle saldature

Il modello con i soli vincoli multipunto non rispetta la rigidezza della saldatura e la distribuzione delle sollecitazioni è conservativa. I picchi di sollecitazione che compaiono all'estremità dei bordi della piastra, negli angoli e negli arrotondamenti, regolano la resistenza lungo l'intera lunghezza della saldatura. Per eliminare l'effetto, tra le piastre viene aggiunto uno speciale elemento elastoplastico. L'elemento rispetta l'altezza, la posizione e l'orientamento della gola di saldatura. Viene inserito il solido di saldatura equivalente con le dimensioni di saldatura corrispondenti. Si applica l'analisi non lineare dei materiali e si determina il comportamento elastoplastico del solido di saldatura equivalente. Lo stato di plasticità è controllato dalle sollecitazioni nella sezione di gola della saldatura. I picchi di sollecitazione sono ridistribuiti lungo la parte più lunga della lunghezza della saldatura.

Il modello elastoplastico delle saldature fornisce valori reali di sollecitazione e non è necessario fare una media o interpolare le sollecitazioni. I valori calcolati in corrispondenza dell'elemento di saldatura più sollecitato vengono utilizzati direttamente per le verifiche del componente di saldatura. In questo modo, non è necessario ridurre la resistenza delle saldature con orientamento multiplo, delle saldature su ali non irrigidite o delle saldature lunghe.

Vincolo tra elemento di saldatura e nodi della mesh

Le saldature in generale, pur avvalendosi della ridistribuzione plastica, possono essere impostate come continue, parziali e intermittenti. Le saldature continue si estendono su tutta la lunghezza del bordo, quelle parziali consentono di impostare gli offset da entrambi i lati del bordo, mentre le saldature intermittenti possono essere impostate con una lunghezza e un intervallo.

Connessioni con bulloni e bulloni precaricati

Bulloni

Nel Metodo agli Elementi Finiti Basato sulle Componenti (CBFEM), il bullone, con il suo comportamento in trazione, taglio e bearing, è il componente descritto dalle molle dipendenti non lineari. Il gruppo bullone è composto da bullone, rondella e dado ed è simulato da una molla non lineare, da elementi a corpo rigido e da elementi di intervallo (gap elements).

Bullone in trazione

Il bullone in trazione è descritto da una molla con la sua rigidezza  assiale iniziale, la resistenza di progetto, l'innescarsi dello snervamento e la capacità di deformazione. La rigidezza assiale iniziale è ricavata analiticamente nella linea guida VDI2230 e in Agerskov (1976).

\[D_{Lb} =\frac{L_s+0.4d_b}{EA_{ss}}\]

\[A_{pp}=\frac{0.75D_H(L_w-D_H)}{D_{W1}^2-D_{W2}^2}\]

\[A_{P1}=\frac{\pi}{4}(D_H^2-D_{W1}^2)\]

\[A_{P2}=\frac{1}{2}(D_{W2}^2-D_H^2)\tan^{-1}A_{pp}\]

\[A_P=A_{P1}+A_{P2}\]

\[D_{LW}=\frac{L_W}{EA_P}\]

\[k=\frac{1}{D_{LB}+D_{LW}}\]

dove:

• \(d_b\) – diametro del bullone
• \(D_H\) – diametro della testa del bullone
• \(D_{W1}\) – diametro interno della rondella
• \(D_{W2}\) – diametro esterno della rondella
• \(L_W\) – spessore della rondella
• \(L_s\) –  lunghezza della parte non filettata del gambo
• \(A_{ss}\) – area lorda del bullone
• \(E\) – Modulo di elasticità di Young

Il modello corrisponde ai dati sperimentali; si veda Gödrich et al. (2014). Per l’innesco dello snervamento e della capacità di deformazione, si presume che la deformazione plastica si verifichi solamente nella parte filettata del gambo del bullone.

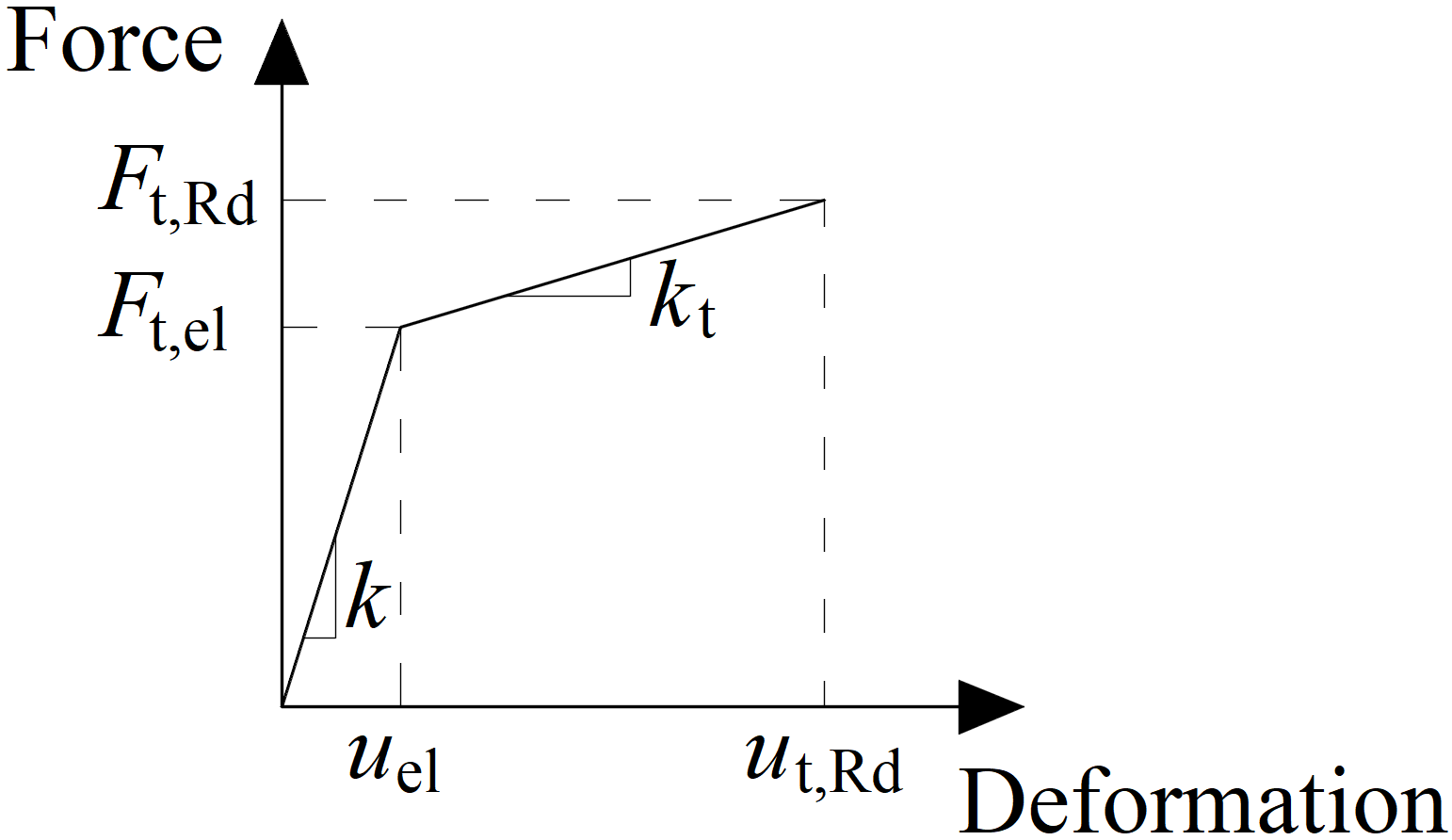
Diagramma forza-deformazione per il carico della piastra

Il diagramma forza-deformazione viene costruito utilizzando le seguenti equazioni:

Rigidezza plastica:

\[ k_t = c_1 k \]

Forza al limite elastico:

\[ F_{t,el} = \frac{F_{t,Rd}}{c_1 c_2 - c_1 +1} \]

Deformazione al limite elastico:

\[ u_{el} = \frac{ F_{t,el} }{k} \]

Deformazione al limite plastico:

\[ u_{t,Rd} = c_2 u_{el} \]

\[ c_1 = \frac{f_{ub} - f_{yb}}{\frac{1}{4} A E - f_{yb}} \]

\[ c_2 = \frac{AE}{4 f_{yb}} \]

dove:

• \(F_{t,Rd}\) – resistenza di progetto del bullone in trazione
• \(f_{yb}\) –  resistenza limite del bullone
• \(f_{ub}\) – resistenza ultima del bullone
• \(A\) – allungamento dopo la frattura

Bullone a taglio

Solo la forza di compressione viene trasferita dal gambo del bullone alla piastra nel foro del bullone. È modellato da interpolazioni tra i nodi del gambo e i nodi sul bordo dei fori. La rigidezza di deformazione dell'elemento shell che modella le piastre distribuisce le forze tra i bulloni e simula il carico adeguato della piastra.

I fori dei bulloni sono considerati standard (predefiniti) o asolati (possono essere impostati nell'editor delle piastre). I bulloni nei fori standard possono trasferire la forza di taglio in tutte le direzioni, mentre i bulloni nei fori asolati hanno una direzione esclusa e possono muoversi liberamente nella direzione selezionata.

La rigidezza iniziale e la resistenza di progetto di un bullone a taglio sono definite dalle seguenti formule:

\[k_{el}=\frac{1}{\frac{1}{k_{11}}+\frac{1}{k_{12}}}\]

\[k_{11} = \frac{8d_b^2f_{ub}}{d_{M16}}\]

\[k_{12}=12k_td_bf_{up}\]

\[k_t=\min \left ( 2.5,\, \frac{1.5t_{min}}{d_{M16}} \right ) \]

\[k_{pl}=\frac{k_{el}}{1000}\]

dove:

• \(d_b\) – diametro del bullone
• \(f_{ub}\) – resistenza ultima del bullone
• \(d_{M16}=16 \textrm{ mm}\) – diametro del bullone di riferimento M16
• \(f_{up}\) – resistenza ultima della piastra collegata
• \(t_{min}\) – spessore minimo della piastra collegata 

The spring representing the bolt in shear has bi-linear force deformation behavior. Initialization of yielding is expected at:

La molla che rappresenta il bullone a taglio ha un comportamento bi-lineare di deformazione della forza. L'inizio dello snervamento è previsto a:

\[F_{V,el}=0.999 F_{V,Rd}\]

La capacità di deformazione è considerata come:

\[\delta_{pl}=\delta_{el}\]

dove:

• \(F_{V,el}\) – resistenza elastica del bullone a taglio
• \(F_{V,Rd}\) – resistenza di progetto del bullone a taglio
• \(\delta_{el}\) – deformazione elastica del bullone a taglio

Interazione tra razione e taglio

L'interazione tra la forza assiale e quella di taglio può essere introdotta direttamente nel modello di analisi. La distribuzione delle forze riflette meglio la realtà (vedi diagramma allegato). I bulloni con un'elevata forza di trazione assorbono meno forza di taglio e viceversa.

Esempio di interazione tra forza assiale e di taglio (EC)

Bulloni precaricati

I bulloni precaricati sono utilizzati nelle unioni ad attrito nei casi in cui è necessario ridurre al minimo la deformabilità della struttura. Il modello di trazione in questo caso è lo stesso dei bulloni standard. La forza di taglio non viene trasferita tramite bearing bensì tramite attrito tra le piastre serrate.

La resistenza allo slittamento di progetto di un bullone precaricato è influenzata da una forza di trazione applicata.

IDEA StatiCa Connection verifica lo stato limite di pre-slittamento dei bulloni precaricati. Se si osserva un effetto di slittamento, i bulloni non soddisfano la verifica. In seguito, deve essere verificato lo stato limite post-slittamento, effettuando una verifica standard dei bulloni in bearing, in cui i fori dei bulloni sono caricati in modo portante e i bulloni in taglio.

L'utente può decidere quale stato limite controllare tra la resistenza allo scorrimento importante o lo stato di post-scorrimento a taglio dei bulloni. Entrambe le verifiche su uno stesso bullone non sono combinate in un'unica soluzione. Si presume che il bullone abbia un comportamento standard dopo uno scorrimento importante e che possa essere verificato con la procedura di carico standard.

Il carico del momento della connessione ha una leggera influenza sulla capacità a taglio. Tuttavia, viene risolta semplicemente in modo separato una verifica dell'attrito su ciascun bullone. Questa verifica è implementata nel componente FEM del bullone. Non vi sono informazioni generali sul fatto che il carico di trazione esterno di ciascun bullone derivi dal momento flettente o dal carico di trazione della connessione.

Distribuzione delle tensioni in una connessione a taglio con bulloni standard

Distribuzione delle tensioni in una connessione ad attrito con bulloni a taglio

Bulloni di ancoraggio

Il bullone di ancoraggio viene modellato con procedimenti simili a quelli dei bulloni strutturali. Il bullone è fissato su un lato del blocco di calcestruzzo. La sua lunghezza, L_b, utilizzata per il calcolo della rigidezza del bullone, viene considerata come la somma della metà dello spessore del dado più lo spessore della rondella t_w,più lo spessore della piastra di base t_bp, più lo spessore della boiacca o dello spazio t_g, e la lunghezza libera inserita nel calcestruzzo, che si prevede pari a 8d , dove d è il diametro del bullone. Il fattore 8 è modificabile in Impostazione codice. Questo valore è conforme al Metodo delle Componenti (EN1993-1-8); la lunghezza libera inserita nel calcestruzzo può essere modificata in Impostazione codice. La rigidezza in trazione è calcolata come k = E A_s / L_b. Il diagramma carico-deformazione del bullone di ancoraggio è mostrato nella figura seguente. I valori secondo la norma ISO 898:2009 sono riassunti nella tabella e nelle formule seguenti.

Diagramma carico-deformazione del bullone di ancoraggio

\[ F_{t,el}=\frac{F_{t,Rd}}{c_1 c_2 - c_1 + 1} \]

\[ k_t = c_1 k; \qquad c_1 = \frac{R_m - R_e}{\left ( \frac{1}{4} A - \frac{R_e}{E} \right )E} \]

\[ u_{el} = \frac{F_{t,el}}{k}; \qquad u_{t,Rd} = c_2 u_{el}; \qquad c_2 = \frac{AE}{4R_e} \]

dove:

• A – allungamento
• E – Modulo di elasticità di Young
• F_t,Rd – resistenza a trazione dell'acciaio dell'ancoraggio
• R_m –  resistenza ultima (a trazione)
• R_e – resistenza limite di snervamento

La rigidezza a taglio del bullone di ancoraggio viene considerata come la rigidezza a taglio del bullone strutturale.

Bulloni di ancoraggio con stand-off

Gli ancoraggi con stand-off possono essere verificati come fase di costruzione prima dell’applicazione del giunto do malta alla base del pilastro o come stato permanente. L'ancoraggio con stand-off è progettato come elemento asta caricato da forza di taglio, momento flettente e forza di compressione o trazione. L'ancoraggio è fissato da entrambi i lati; un lato è 0.5×d sotto il livello del calcestruzzo, l'altro lato è al centro dello spessore della piastra. La lunghezza libera di inflessione è calcolata, in via prudenziale, come il doppio della lunghezza dell'elemento asta. Si utilizza il modulo di sezione plastica. Le forze nell'ancoraggio con stand-off sono state determinate utilizzando l'analisi agli elementi finiti. Il momento flettente dipende dall’indice di rigidezza degli ancoraggi e della piastra di base.

Ancoraggi con stand-off: determinazione del braccio di leva e delle lunghezze libere di inflessione; gli ancoraggi  per sicurezza vengono considerati

Modello strutturale di un blocco di calcestruzzo

Modello del progetto

Nel CBFEM, è conveniente semplificare il blocco di calcestruzzo come elementi di contatto 2D. La connessione tra il calcestruzzo e la piastra di base resiste solo alla compressione. La compressione è trasferita attraverso il modello di sottosuolo Winkler-Pasternak, che rappresenta le deformazioni del blocco di calcestruzzo. La forza di trazione tra la piastra di base e il blocco di calcestruzzo è trasportata dai bulloni di ancoraggio. La forza di taglio è trasferita dall'attrito tra la piastra di base e il blocco di calcestruzzo, dalla chiave di taglio e dalla flessione dei bulloni di ancoraggio e dall'attrito. La resistenza dei bulloni a taglio è valutata analiticamente. L'attrito e la chiave di taglio sono modellati come un vincolo completo a punto singolo nel piano di contatto piastra di base - calcestruzzo.

Rigidezza alla deformazione

La rigidezza del blocco di calcestruzzo può essere prevista per la progettazione delle basi dei pilastri come un emisfero elastico. Il modello di sottosuolo Winkler-Pasternak è comunemente utilizzato per un calcolo semplificato delle fondazioni. La rigidità del sottosuolo viene determinata utilizzando il modulo di elasticità del calcestruzzo e l'altezza effettiva del sottosuolo come:

\[ k = \frac{E_c}{(\alpha_1 + \upsilon) \sqrt{\frac{A_{eff}}{A_{ref}}}} \left( \frac{1}{\frac{h}{a_2 d} + a_3}+a_4 \right) \]

dove:

• k - rigidezza del sottosuolo nel calcestruzzo a compressione
• E_c - modulo di elasticità del calcestruzzo
• υ - coefficiente di Poisson del blocco di calcestruzzo
• A_eff - area effettiva in compressione
• A_ref = 1 m² - area di riferimento
• d - larghezza della piastra di base
• h - altezza del blocco di calcestruzzo
• a₁ = 1,65; a₂ = 0,5; a₃ = 0,3; a₄ = 1,0 - coefficienti

Nella formula devono essere utilizzate le unità del Sistema Internazionale, l'unità risultante è N/m³.

Trasferimento del carico di taglio alla piastra di base

Il carico di taglio sulla piastra di base può essere trasferito in tre modi:

• Attrito
• Ferro a taglio
• Ancoraggi

L'utente può scegliere il modo in cui è trasferito il taglio modificando il funzionamento della piastra di base. Il software non consente alcuna combinazione di modalità di trasferimento del carico, tuttavia la norma EN 1993-1-8 - Cl. 6.2.2 e la norma Fib 58 - Capitolo 4.2 consentono di combinare il trasferimento del taglio mediante ancoraggi e attrito in determinate condizioni. In generale, è prudente trascurare l'attrito nella progettazione degli ancoraggi, anche se in alcuni casi può portare a una sottostima della fessurazione del calcestruzzo a livello di esercizio. Di norma, la resistenza all'attrito dovrebbe essere trascurata se:

• lo spessore dello strato del giunto di malta supera la metà del diametro dell'ancoraggio,
• la capacità dell'ancoraggio è regolata da una condizione di vicinanza al bordo,
• l'ancoraggio è destinato a resistere a carichi sismici.

La combinazione con un ferro a taglio non dovrebbe mai essere consentita a causa della compatibilità di deformazione.

Trasferimento del carico di taglio per attrito

La resistenza al taglio è uguale al fattore di sicurezza della resistenza moltiplicato per il coefficiente di attrito (modificabile in Impostazione codice) e carico di compressione. Il carico di compressione comprende tutte le forze, ad es. nel caso di una base di colonna caricata da una forza di compressione e da un momento flettente, il carico di compressione utilizzato per la resistenza al taglio per attrito potrebbe essere superiore alla forza di compressione applicata.

Trasferimento del carico di taglio tramite il ferro a taglio

Il ferro di taglio è simulata come un tronchetto di membratura incassato nel calcestruzzo sotto la piastra di base. Si stima che il carico di taglio sia trasferito mediante una distribuzione uniforme del carico che agisce sull'intera porzione dell'ansa di taglio annegata nel blocco di calcestruzzo, vale a dire che tutti i nodi dell'ansa di taglio al di sotto della superficie del calcestruzzo sono caricati uniformemente. Non si assume che la porzione di chiave di taglio sopra la superficie del calcestruzzo di malta trasferisca il carico di taglio.

Si tenga presente che il braccio di leva tra il carico di taglio applicato (alla piastra di base) e la resistenza al taglio (metà altezza dell'ansa a taglio annegata nel calcestruzzo) provoca un momento flettente che deve essere trasferito mediante forze di compressione nel calcestruzzo e forze di trazione negli ancoraggi.

Il ferro a taglio è costituito da elementi finiti shell ed è verificato come una piastra regolare. Inoltre, le saldature del ferro a taglio alla piastra di base sono verificate utilizzando le procedure standard di IDEA StatiCa Connection. Il calcolo manuale di solito assume la teoria della trave per il ferro a taglio, anche se non è accurato perché il rapporto lunghezza/larghezza è molto piccolo per il ferro a taglio. Pertanto, potrebbe esserci una differenza significativa tra IDEA StatiCa Connection e il calcolo manuale.

Trasferimento del carico di taglio da parte degli ancoraggi

La resistenza al taglio è determinata dalla resistenza al taglio degli ancoraggi. La resistenza dell'acciaio degli ancoraggi ha una curva di carico-deformazione elastoplastica, ma le modalità di rottura del calcestruzzo sono considerate perfettamente fragili.

Modello di analisi di IDEA StatiCa

Modello di analisi dei giunti in acciaio

Il metodo CBFEM (Component Based Finite Element Model) consente di analizzare rapidamente giunti di diverse forme e configurazioni. Il modello è costituito da elementi a cui viene applicato il carico e da operazioni di produzione (compresi gli elementi di irrigidimento), che servono a collegare gli elementi tra loro. Le membrature non devono essere confuse con le operazioni di produzione perché i loro bordi tagliati sono collegati tramite link rigidi al nodo della connessione, quindi non si deformano correttamente se usati al posto delle operazioni di produzione (elementi di irrigidimento).

Il modello FEM analizzato viene generato automaticamente. Il progettista non crea il modello FEM, ma crea la giunzione usando le operazioni di produzione - si veda la figura.

Operazioni di produzione/elementi che possono essere utilizzati per costruire il giunto

Ogni operazione di produzione aggiunge nuovi elementi alla connessione: tagli, piastre, bulloni, saldature.

Elementi portanti e vincoli

Una membratura del giunto è sempre impostata come "portante". Tutte le altre membrature sono "collegate". La membratura portante può essere scelta dal progettista e può essere "continua" o "finita" nel nodo. Gli elementi "finiti" sono vincolati su un'estremità, mentre gli elementi "continui" sono vincolati su entrambe le estremità.

Le membrature collegate possono essere di diversi tipo, a seconda del carico che l'elemento può sopportare:

• Tipo N-Vy-Vz-Mx-My-Mz – la membratura è in grado di trasferire tutte e 6 le componenti delle forze interne
• Tipo N-Vy-Mz – la membratura è in grado di trasferire solo il carico nel piano XY – forze interne N, V_y, M_z
• Tipo N-Vz-My – la membratura è in grado di trasferire solo il carico nel piano XZ  – forze interne N, V_z, M_y
• Tipo N-Vy-Vz – la membratura è in grado di trasferire solo sforzo normale N e sforzi di taglio V_y e V_z

La connessione piastra con piastra trasferisce tutte le componenti delle forze interne

La connessione con piatto rinforzato può trasferire solo i carichi nel piano XZ - forze interne N, V_y, M_y

La connessione a fazzoletto di un elemento di travatura reticolare può trasferire solo la forza assiale N e le forze di taglio V_y e V_z

Ogni giunto è in stato di equilibrio durante l'analisi della struttura a telaio. Se le forze di estremità delle singole membrature vengono applicate al modello CBFEM dettagliato, anche lo stato di equilibrio viene rispettato. Pertanto, non sarebbe necessario definire i supporti nel modello di analisi. Tuttavia, per ragioni pratiche, l'appoggio che resiste a tutte le traslazioni è definito nella prima estremità dell'elemento portante. Non influenza né lo stato di sollecitazione né le forze interne al giunto, ma solo la presentazione delle deformazioni.

Per evitare l'insorgere di meccanismi instabili, alle estremità degli elementi collegati si definiscono tipi di supporto appropriati, che rispettino il tipo dei singoli elementi.

La lunghezza predefinita di ogni elemento è il doppio della sua altezza. La lunghezza di un elemento dovrebbe essere almeno 1× l'altezza dell'elemento dopo l'ultima operazione di produzione (saldatura, apertura, irrigidimento, ecc.) a causa delle deformazioni corrette dopo i collegamenti rigidi che collegano l'estremità tagliata di un elemento al nodo di connessione.

Equilibrio del nodo nel modello FEM 3D

I carichi in qualsiasi nodo del modello strutturale devono essere in equilibrio. Qualsiasi forza non equilibrata viene assorbita dai vincoli. Si raccomanda di utilizzare una combinazione di carichi invece di un inviluppo delle forze interne.

Ogni nodo del modello FEM 3D deve essere in equilibrio. Il requisito dell'equilibrio è corretto, tuttavia non è necessario per la progettazione di giunti semplici. Una membratura del giunto è sempre "resistente o portante", mentre gli altri sono connessi. Se si verifica solo la connessione delle membrature collegate, non è necessario mantenere l'equilibrio. Sono quindi disponibili due modalità per inserire il carico:

• Semplificata: per questa modalità, la membratura resistente è vincolata (elemento continuo su entrambi i lati) e il carico non è definito sulla membratura resistente
• Avanzata (esatta con verifica dell'equilibrio):  la membratura resistente è vincolata a un'estremità, i carichi sono applicati a tutte le membrature e si deve rispettare l'equilibrio

La modalità può essere cambiata cliccando sul pulsante Carichi in equilibrio.

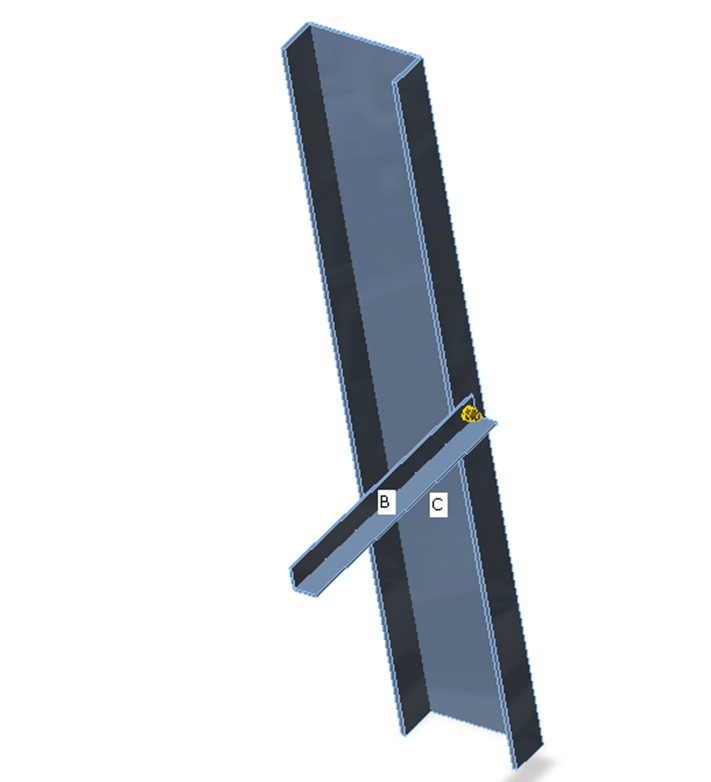
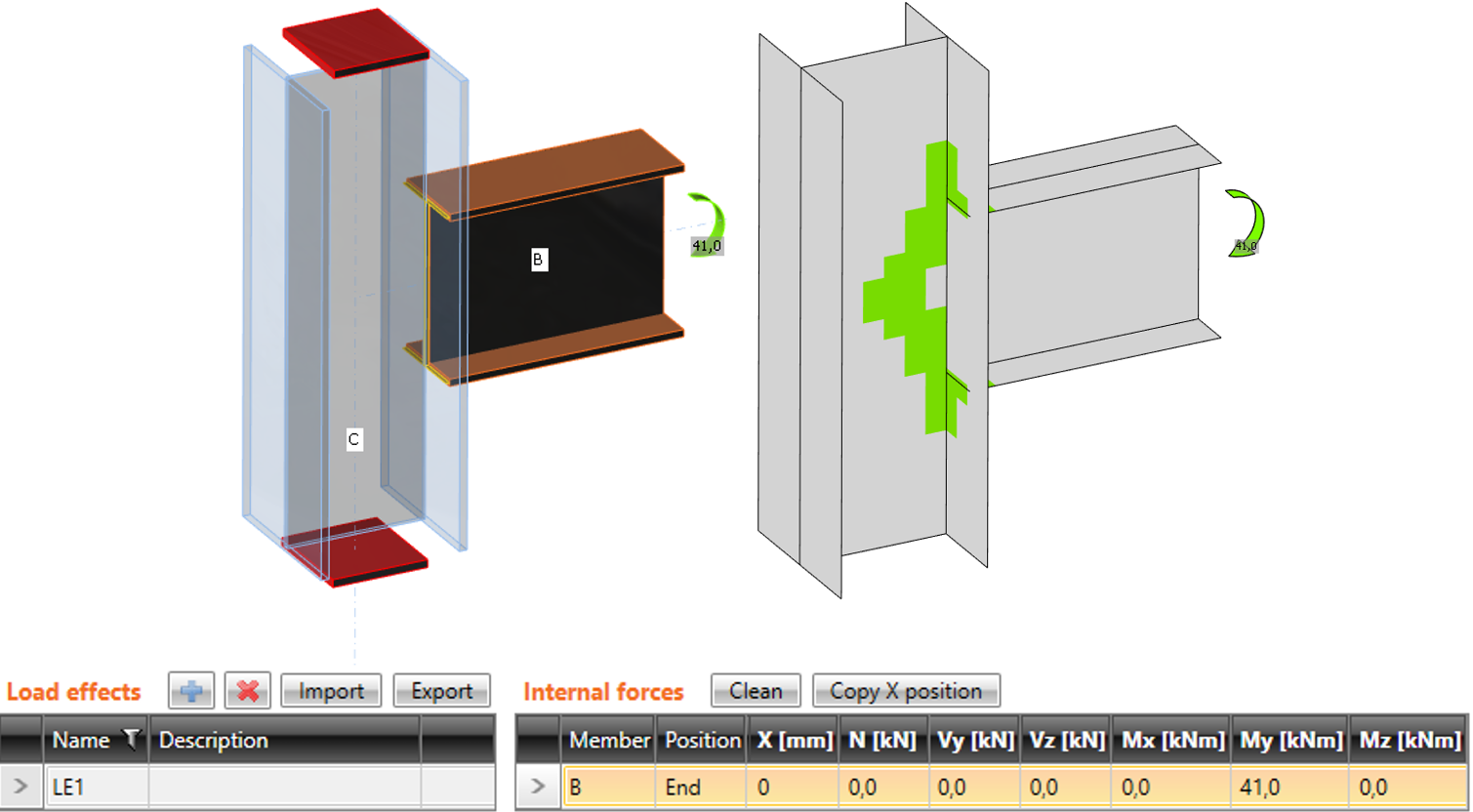
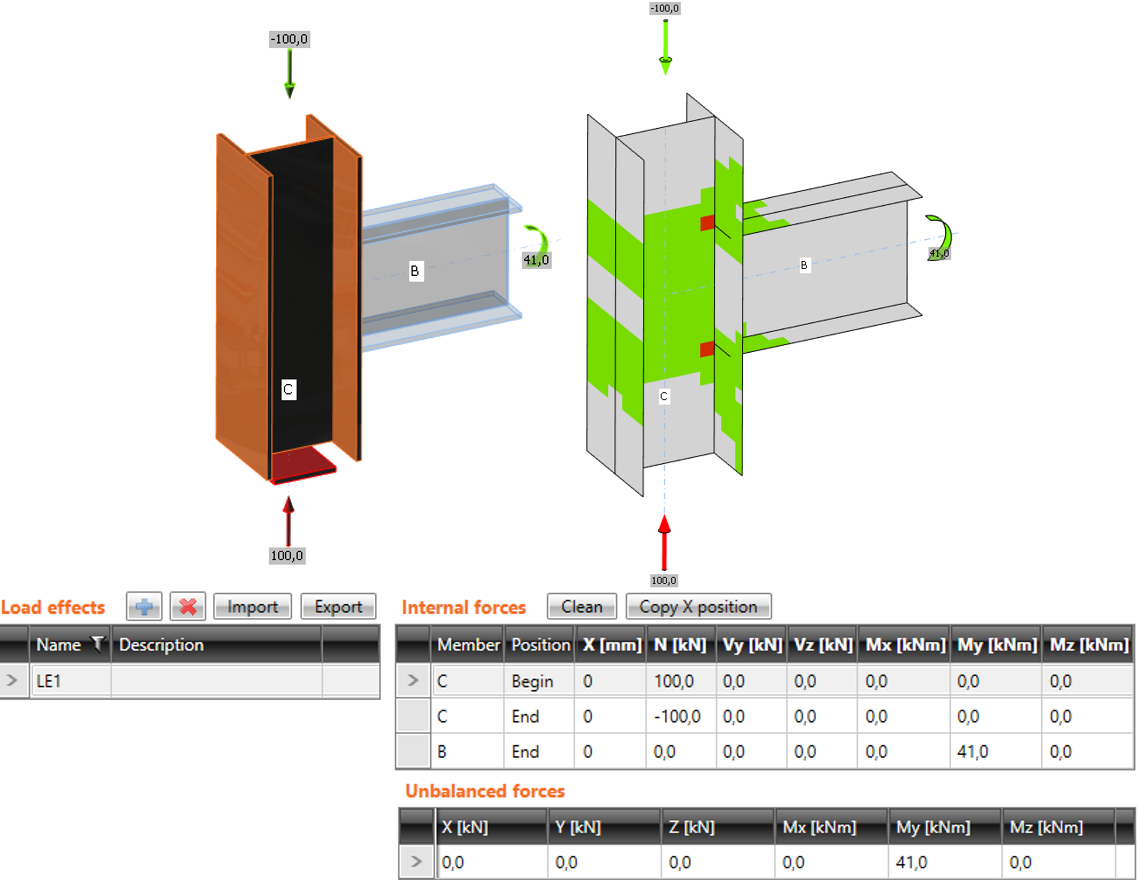
La differenza tra le due modalità è illustrata nel seguente esempio di connessione a T. La trave è soggetta a un momento flettente finale di 41 kNm. Sul pilastro agisce anche una forza normale di compressione di 100 kN. Nel caso della modalità semplificata, la forza normale non viene presa in considerazione perché il pilastro è vincolato su entrambe le estremità. Il programma mostra solo l'effetto del momento flettente della trave. Gli effetti della forza normale sono analizzati solo nella modalità completa e sono mostrati nei risultati.

Inserimento semplificato: la forza normale nel pilastro NON viene presa in considerazione

Inserimento avanzato: si tiene conto della forza normale nel pilastro

Il metodo semplificato è più facile per l'utente, ma può essere utilizzato solo quando l'utente è interessato a studiare gli elementi della connessione e non il comportamento dell'intero giunto.

Nei casi in cui la membratura portante sia soggetto a un carico notevole e vicino alla sua capacità limite, è necessario avvalersi della modalità avanzata che rispetta tutte le forze interne al giunto.

Forze interne nelle connessioni in acciaio

Le forze di estremità di una membratura del modello di analisi del telaio vengono trasferite alle estremità dei segmenti della membratura. Durante il trasferimento vengono rispettate le eccentricità degli elementi causate dalla progettazione del giunto.

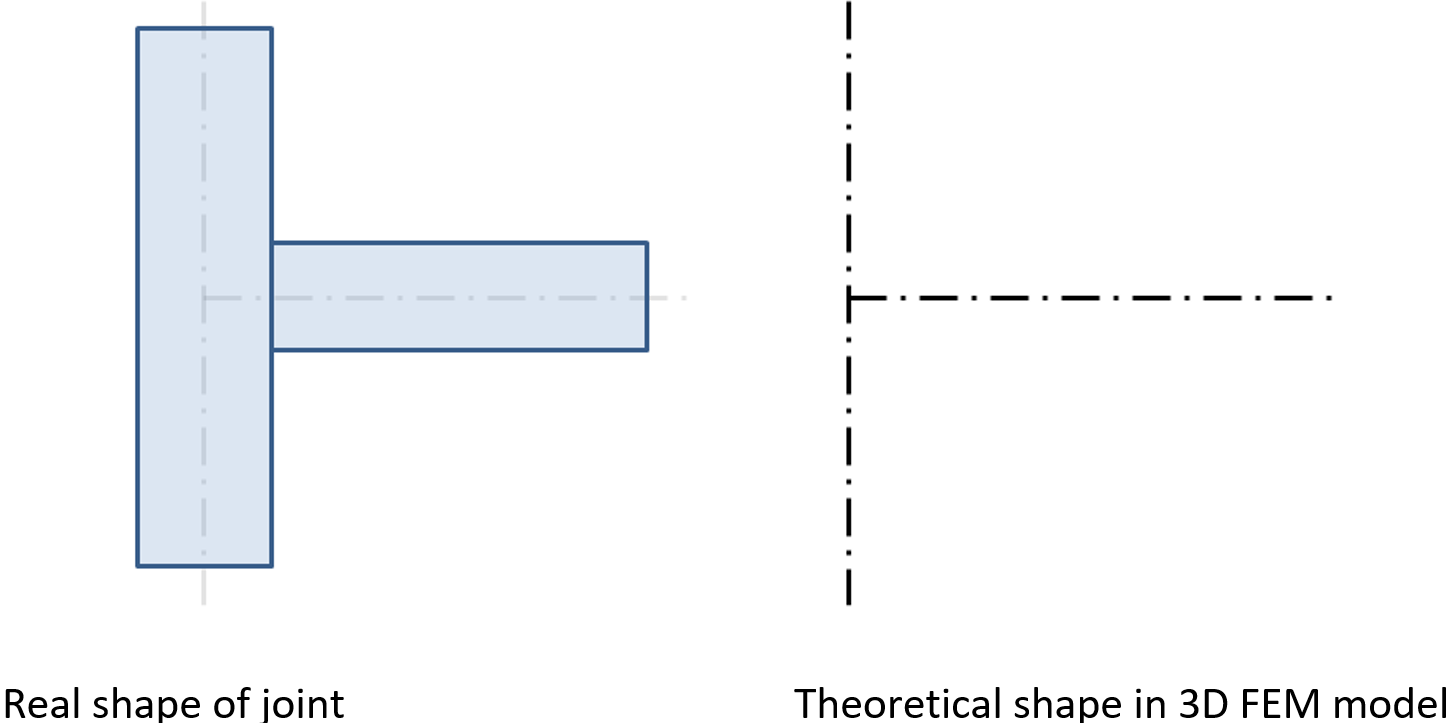
Il modello di analisi creato dal metodo CBFEM corrisponde in modo molto preciso al giunto reale, mentre l'analisi delle forze interne viene eseguita su un modello FEM 3D molto idealizzato, in cui i modelli delle singole travi sono creati utilizzando le linee d’asse e i giunti con nodi immateriali.

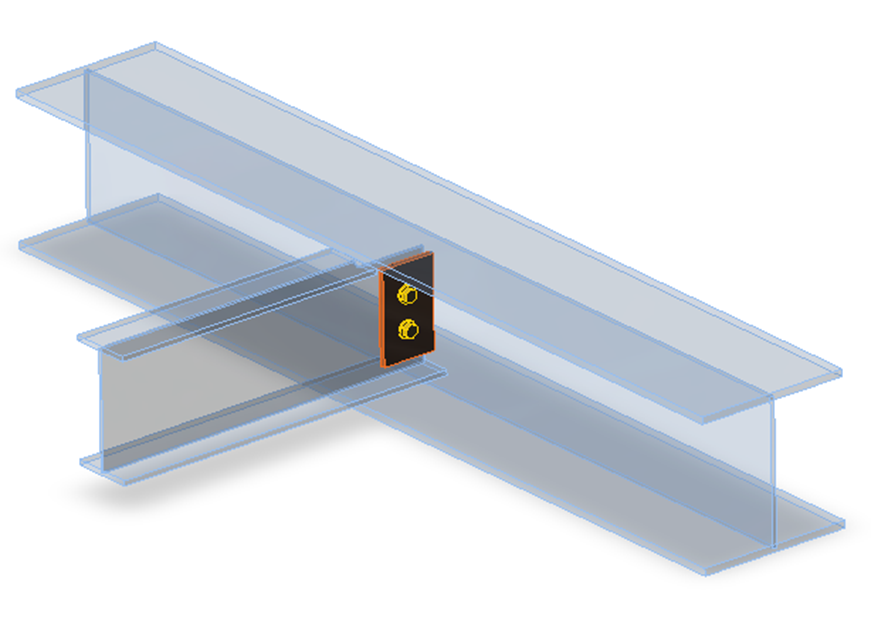
Giunto di un pilastro verticale e di una trave orizzontale

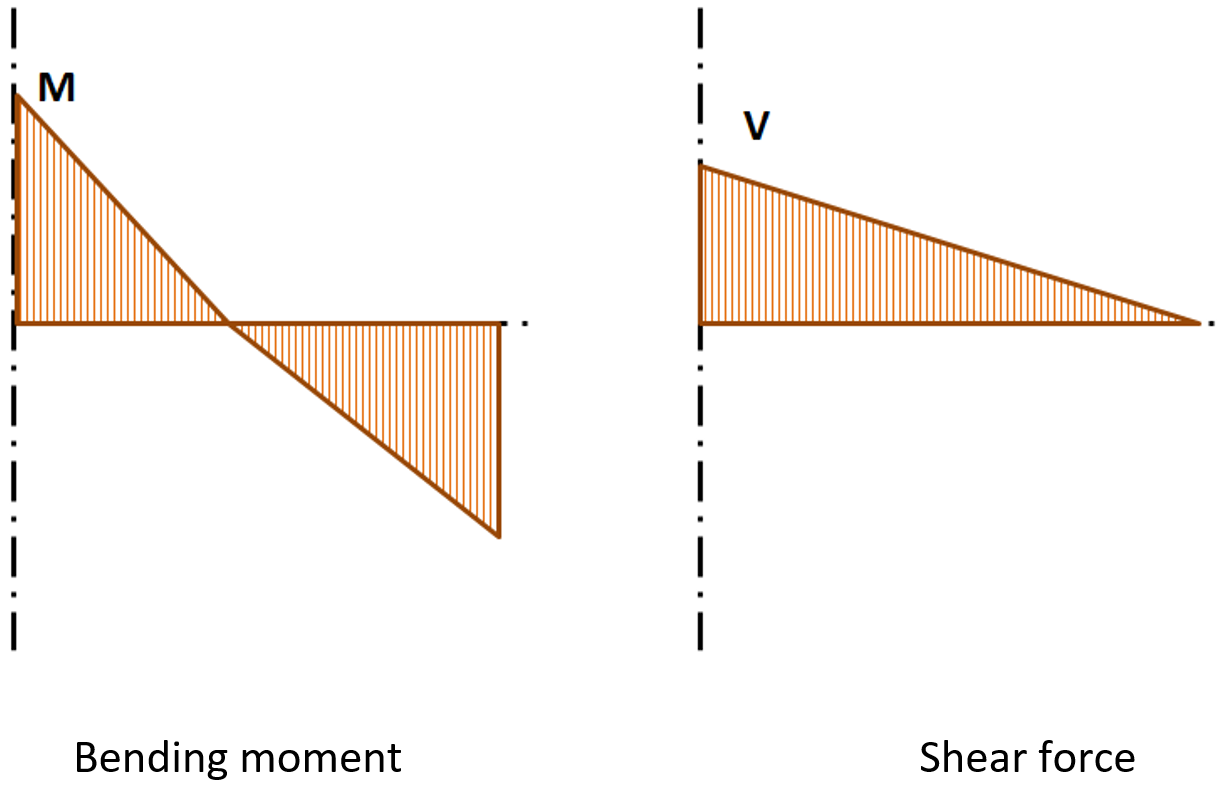
Le forze interne sono analizzate utilizzando membrature in 1D nel modello 3D. Nella figura seguente è riportato un esempio di forze interne.

Forze interne nella trave orizzontale; M e V sono le forze di estremità nell'unione

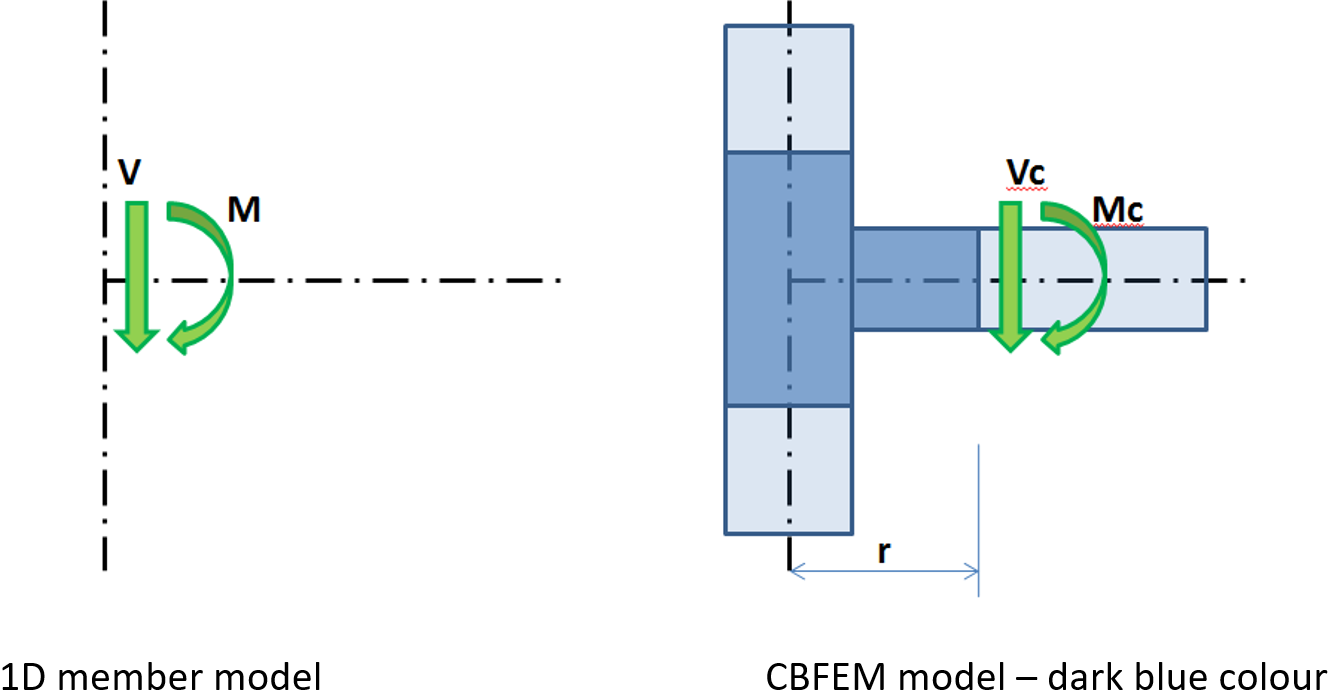
Gli effetti causati da un elemento sull'unione sono importanti per la progettazione dell'unione (connessione). Gli effetti sono illustrati nella figura seguente:

Effetti dell'elemento sull'unione ; il modello CBFEM è disegnato in colore blu scuro

Il momento M e la forza di taglio V agiscono sul giunto teorico. Il punto del giunto teorico non esiste nel modello CBFEM, quindi qui il carico non può essere applicato. Il modello deve essere sottoposto alle forze M e V, che devono essere trasferite all'estremità del segmento nella distanza r

M_c = M – V ∙ r

V_c = V

Nel modello CBFEM, la sezione di estremità del segmento è soggetta al momento M_c e alla forza V_c.

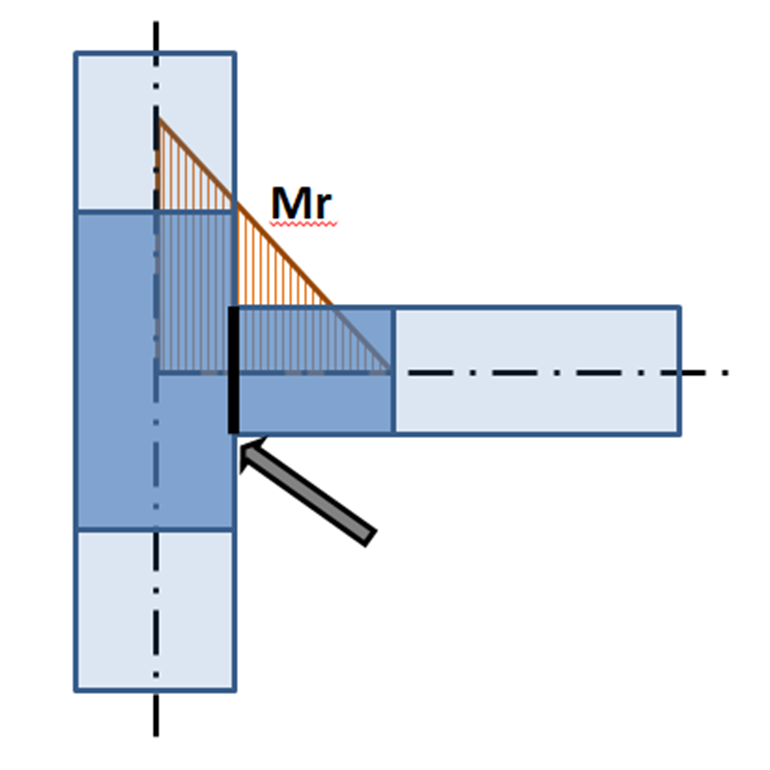
Quando si progetta il giunto, è necessario determinare e rispettare la sua posizione reale rispetto al punto teorico del giunto. Le forze interne nella posizione del giunto reale sono per lo più diverse dalle forze interne nel punto teorico del giunto. Grazie alla precisione del modello CBFEM, la progettazione viene eseguita su forze ridotte; si veda il momento M_r nella figura seguente:

Momento flettente nel modello CBFEM: la freccia indica la posizione reale della connessione

Quando si carica il giunto, la soluzione del giunto reale deve corrispondere al modello teorico utilizzato per il calcolo delle forze interne. Per i giunti rigidi tale condizione è soddisfatta, ma la situazione può essere completamente diversa per le cerniere.

Posizione della cerniera nel modello FEM 3D teorico e nella struttura reale

La figura precedente illustra la posizione della cerniera nel modello teorico degli elementi in 1D, che differisce dalla posizione reale nella struttura. Il modello teorico non corrisponde alla realtà. Quando si applicano le forze interne calcolate, al giunto spostato viene applicato un momento flettente significativo e il giunto progettato risulta troppo grande o non può essere progettato. La soluzione è semplice: entrambi i modelli devono corrispondere. O la cerniera nel modello di membratura in 1D deve essere definita nella posizione corretta, oppure la forza di taglio deve essere spostata per ottenere un momento zero nella posizione della cerniera.

Distribuzione del momento flettente sulla trave spostata: il momento zero è nella posizione della cerniera

Lo spostamento della forza di taglio può essere definito nella tabella per la definizione della forza interna.

La posizione dell'effetto del carico ha una grande influenza sulla corretta progettazione della connessione. Per evitare qualsiasi malinteso, consentiamo all'utente di selezionare tre opzioni: Nodo / Bulloni / Posizione.

Si noti che quando si seleziona l'opzione Nodo, le forze vengono applicate all'estremità di un elemento selezionato, che di solito si trova nel nodo teorico, a meno che l'offset dell'elemento selezionato non sia impostato nella geometria.

Importazione dei carichi da programmi FEA

IDEA StatiCa consente di importare le forze interne da programmi FEA di terze parti. I programmi FEA utilizzano un inviluppo delle forze interne provenienti da combinazioni. IDEA StatiCa Connection è un programma che risolve il giunto in acciaio in modo non lineare (modello elastico/plastico del materiale). Pertanto, non possono essere utilizzate combinazioni di inviluppi. IDEA StatiCa ricerca gli estremi delle forze interne(N, V_y, V_z, M_x, M_y, M_z) in tutte le combinazioni alle estremità di tutti gli elementi collegati al giunto. Per ogni valore estremo, vengono utilizzate anche tutte le altre forze interne di quella combinazione in tutti gli elementi rimanenti. Idea StatiCa determina la combinazione peggiore per ogni componente (piastra, saldatura, bullone ecc.) della connessione.

L'utente può modificare questo elenco di casi di carico. Può lavorare con le combinazioni nella procedura guidata (o nel BIM), oppure può eliminare alcuni casi direttamente in IDEA StatiCa Connection.

Attenzione!

È necessario tenere conto delle forze interne non equilibrate durante l'importazione. Ciò può accadere nei seguenti casi:

• La forza nodale è stata applicata alla posizione del nodo analizzato. Il software non è in grado di individuare quale elemento debba trasferire tale forza nodale e, pertanto, non ne tiene conto nel modello di analisi. Soluzione: Non utilizzare le forze nodali nell'analisi complessiva. Se necessario, la forza deve essere aggiunta manualmente a una membratura selezionata come sforzo normale o di taglio.
• L'elemento caricato non in acciaio (solitamente in legno o calcestruzzo) è collegato al nodo in esame. Tale elemento non viene considerato nell'analisi e le sue forze interne vengono ignorate. Soluzione: Sostituire l'elemento in calcestruzzo con un blocco in calcestruzzo e un ancoraggio.
• Il nodo è una parte di una soletta o di un muro (solitamente in calcestruzzo). La soletta o il muro non fanno parte del modello e le relative forze interne vengono ignorate. Soluzione: Sostituire la soletta o il muro in calcestruzzo con un blocco in calcestruzzo e un ancoraggio.
• Alcune membrature sono collegate al nodo analizzato tramite collegamenti rigidi. Tali membrature non sono incluse nel modello e le loro forze interne vengono ignorate. Soluzione: Aggiungere manualmente queste membrature all'elenco delle membrature collegate.
• Il software analizza i casi di carico sismico. Per la risoluzione della sismicità, la maggior parte dei software FEA dispone dell'analisi modale. Solitamente, i risultati delle forze interne dei casi di carico sismico forniscono solo gli inviluppi delle forze interne nelle sezioni. A causa del metodo di valutazione (radice quadrata della somma dei quadrati), le forze interne sono tutte positive e non è possibile trovare le forze corrispondenti all'estremo selezionato. Non è possibile raggiungere un equilibrio delle forze interne. Soluzione: Modificare manualmente il segno positivo di alcune forze interne.

Analisi della resistenza dei giunti in acciaio

L'analisi della resistenza è l'analisi dei giunti più importante. Le verifiche di deformazione delle piastre e le verifiche normative dei componenti sono eseguite mediante analisi elastoplastica.

L'analisi dei giunti è non lineare per il materiale. Gli incrementi di carico vengono applicati gradualmente e si ricerca lo stato di sollecitazione. Esistono due modalità di analisi opzionali in IDEA StatiCa Connection:

• La risposta della struttura (giunto) al carico complessivo. In questa modalità, viene applicato tutto il carico definito (100%) e viene calcolato il corrispondente stato di tensione e deformazione.

• L'analisi termina al raggiungimento dello stato limite ultimo. Deve essere selezionata l’opzione "Ferma alla deformazione limite" in Impostazione codice. Tale stato si presenta quando la deformazione plastica raggiunge il limite definito. Se il carico definito è superiore alla capacità calcolata, l'analisi viene contrassegnata come non soddisfacente e viene mostrata la percentuale di carico utilizzato. Si noti che la resistenza analitica dei componenti, ad esempio dei bulloni, può essere superata.

La seconda modalità è più adatta alla progettazione pratica. La prima è preferibile per un'analisi dettagliata di giunti complessi.

Analisi della rigidezza e della capacità di deformazione dei giunti in acciaio

I giunti sono classificati in base alla rigidezza: rigidi, semirigidi e a incernierati. L'ingegnere deve assicurarsi che la rigidezza del giunto confermi quella impostata nel software CAE.

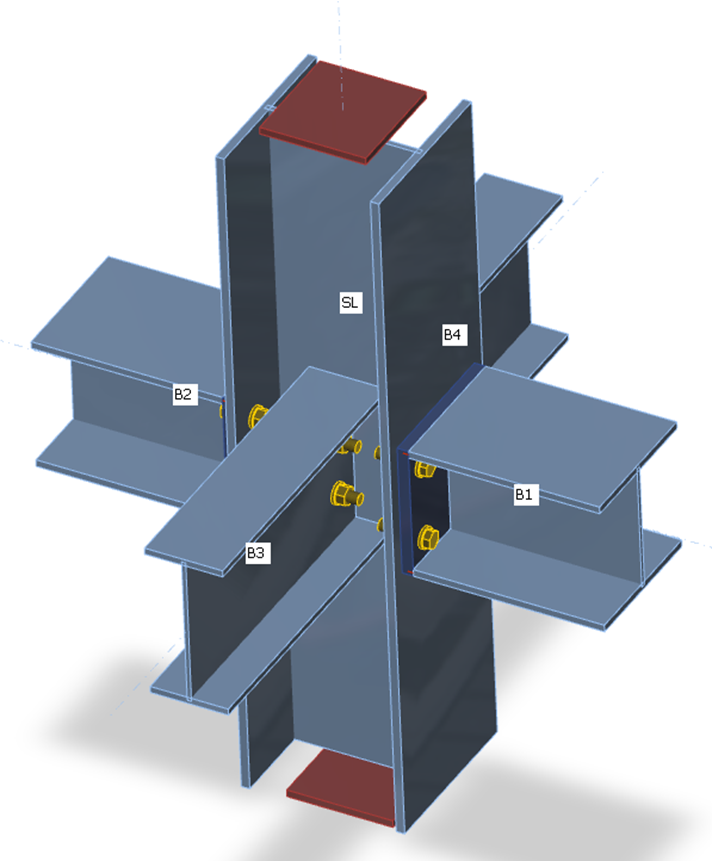
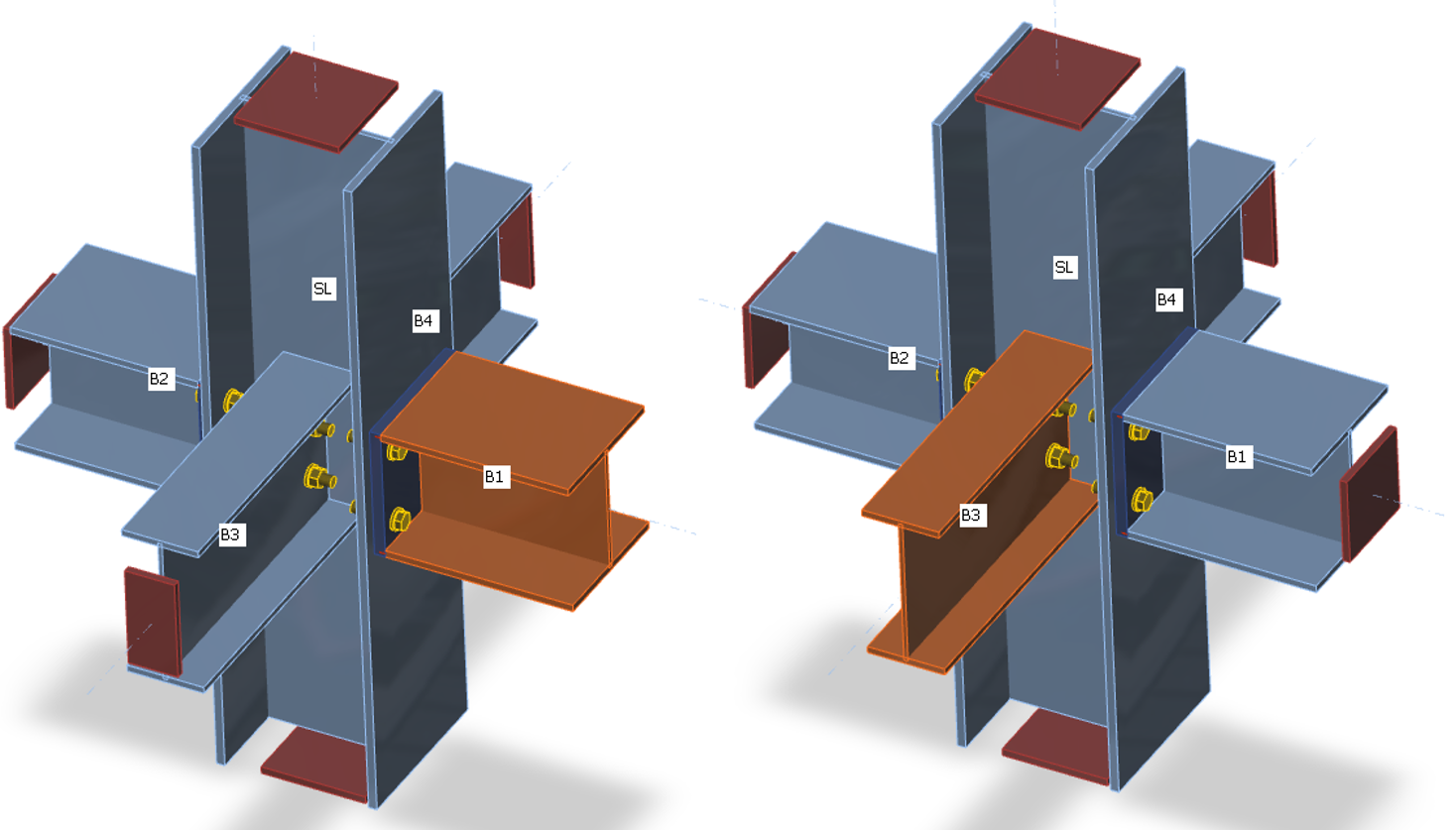
Il metodo CBFEM analizza la rigidezza di connessione dei singoli elementi del giunto. Per un'analisi corretta della rigidezza, è necessario creare un modello di analisi separato per ciascun elemento analizzato. In questo modo, l'analisi della rigidezza non è influenzata dalla rigidezza degli altri elementi del giunto, ma solo dal nodo stesso e dalla costruzione della connessione della membratura analizzata. Mentre la membratura portante presenta vincoli per l'analisi di resistenza (membratura SL nella figura seguente), tutte le membrature, eccetto quella analizzata, presentano vincoli per l'analisi di rigidezza (si vedano le due figure seguenti per l'analisi di rigidezza degli elementi B1 e B3). L'eccezione è rappresentata dalla base del pilastro, dove i vincoli sono forniti dalla fondazione in calcestruzzo, solo la membratura analizzata è soggetta a carico e le altre hanno vincoli solo in base al relativo tipo di modello.

Vincoli su membrature per l'analisi di resistenza

Vincoli su membrature per l'analisi di resistenza della membratura B1

Vincoli su membrature per l'analisi di resistenza della membratura B3

I carichi possono essere applicati solo alla membratura analizzata. Se viene definito il momento flettente M_y, si analizza la rigidezza rotazionale intorno all'asse y. Se viene definito il momento flettente M_z, si analizza la rigidezza rotazionale intorno all'asse z. Se viene definita la forza assiale N, si analizza la rigidezza assiale della connessione.

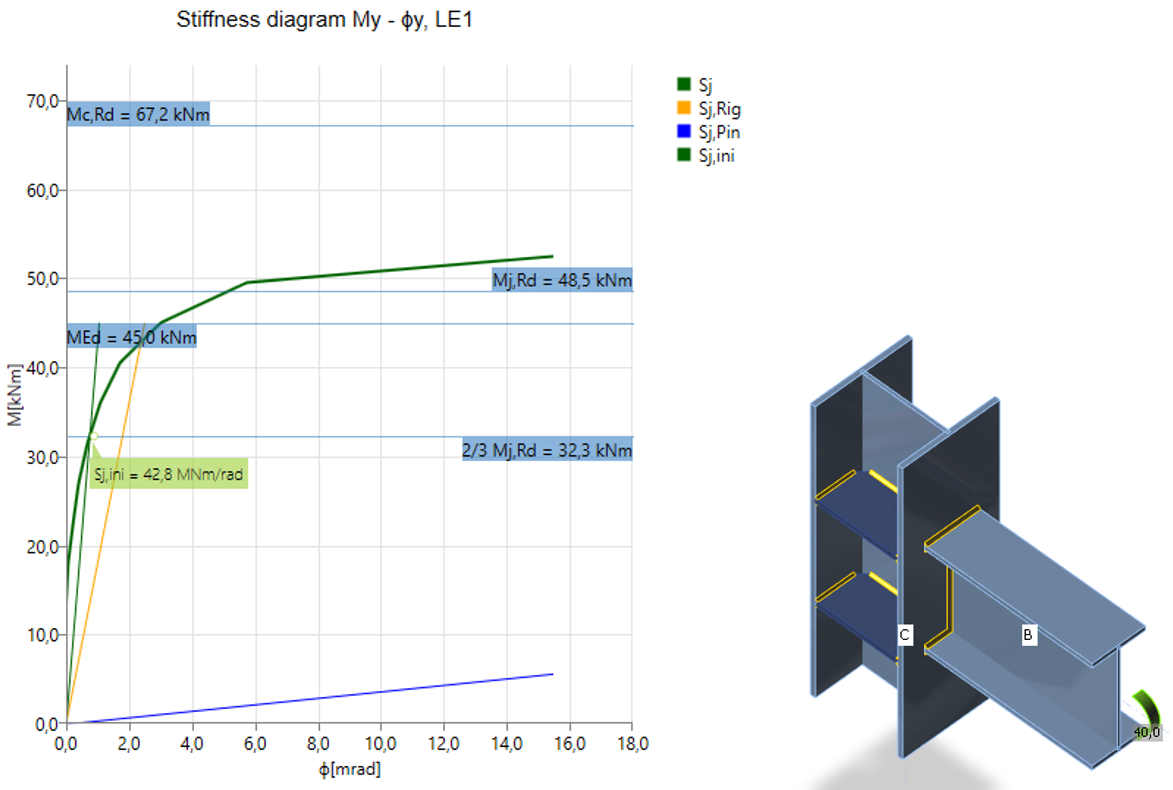
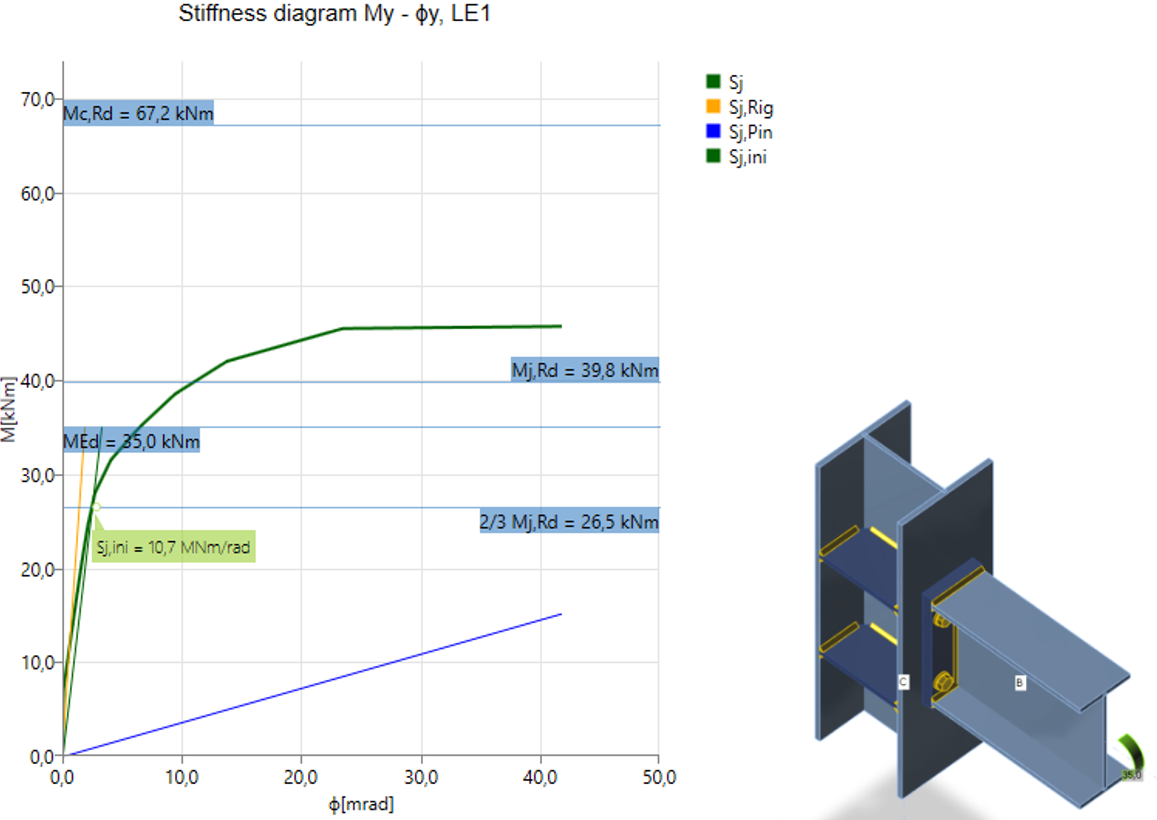
Il programma genera automaticamente un diagramma completo, che viene visualizzato direttamente nell'interfaccia grafica e può essere aggiunto come output nella relazione di calcolo. Per carichi di progetto specifici, può essere studiata la rigidezza rotazionale o assiale. IDEA StatiCa Connection può gestire anche l'interazione delle altre forze interne.

Il diagramma mostra:

• Livello di carico di progetto M_Ed
• Valore limite della capacità di connessione per una deformazione equivalente del 5% M_j,Rd; il limite per la deformazione plastica può essere modificato in Impostazione codice
• Il valore limite della capacità dell'elemento collegato (utile anche per la progettazione sismica) M_c,Rd
• 2/3 della capacità limite per il calcolo della rigidezza iniziale
• Valore della rigidezza iniziale S_j,ini
• Valore della rigidezza secante S_js
• Limiti per la classificazione delle connessioni, rigide e a cerniera
• Deformazione rotazionale Φ
• Capacità rotazionale Φ_c

Connessione rigida saldata

SConnessione semirigida bullonata

Dopo aver raggiunto il 5% di deformazione a taglio nel pannello d'anima del pilastro, le zone plastiche si propagano rapidamente

Il giunto viene classificato in base alla sua rigidezza in giunto rigido, semirigido o a cerniera, secondo il codice pertinente. Per la membratura analizzata può essere impostata la lunghezza teorica:

Come vengono applicati i carichi?

Nell'analisi di rigidezza viene sottoposta a carico e studiata una sola membratura. La membratura analizzata può essere sottoposta a:

• Sforzo normale N
• Sforzi di taglio V_y e V_z
• Momenti flettenti M_y e M_z
• Torsione M_x

Tutti gli effetti del carico sono applicati simultaneamente. Se i carichi applicati sono troppo piccoli, vengono tutti aumentati di un fattore in modo da raggiungere la resistenza del giunto. Quando si creano i diagrammi momento-rotazione o carico-deformazione, tutti gli effetti del carico vengono aumentati in modo proporzionale. 

Ad esempio, la membratura analizzata è sottoposta a:

• Sforzo normale N = 50 kN
• Sforzo di taglio V_z = -80 kN
• Momento flettente M_y = 30 kNm

Le resistenze della membratura sono:

• Resistenza normale N_R = 2 111 kN
• Resistenza al taglio V_z,R = 763 kN
• Resistenza al momento flettente M_y,R = 226 kNm

I carichi vengono moltiplicati per un fattore:

\[ \alpha = \textrm{min} \left \{ \frac{N_R}{N}, \, \frac{M_{y,R}}{M_y}, \, \frac{M_{z,R}}{M_z} \right \}  \]

Si noti che, se lo sforzo di taglio non è applicato sul nodo, cioè agisce su un braccio di leva, il momento flettente è influenzato. Momento flettente sul nodo, visto in un modello fil di ferro, viene utilizzato come carico impostato.

In questo esempio, il fattore è \( \alpha = 7.53 \). I carichi impostati vengono moltiplicati e poi applicati per step, e si tiene traccia dei risultati nel diagramma di rigidezza. I carichi applicati sono suddivisi in 12 step e, quando la connessione si avvicina alla resistenza, gli step vengono ulteriormente affinati. L'esempio dei primi tre step è riportato nella tabella seguente:

	Carichi impostati	Carichi applicati	Primo step	Secondo step	Terzo step
		100%	8.33%	16.67%	25.00%
N	50	377	31	63	94
Vy	0	0	0	0	0
Vz	-80	-603	-50	-100	-151
Mx	0	0	0	0	0
My	30	226	19	38	57
Mz	0	0	0	0	0

Capacità di deformazione

La capacità di deformazione/duttilità δ_Cd costituisce, insieme alla resistenza e alla rigidezza, uno dei tre parametri fondamentali che descrivono il comportamento delle connessioni. Nelle connessioni resistenti al momento, la duttilità si ottiene grazie a una sufficiente capacità di rotazione φ_Cd. La capacità di deformazione/rotazione viene calcolata separatamente per ogni connessione del giunto.

Il software stima la capacità di deformazione come un punto in cui si verifica una delle seguenti condizioni:

• Si raggiunge la resistenza del bullone o dell'ancoraggio in trazione, a taglio o nell'interazione tensione/taglio
• Si raggiunge la resistenza di saldatura
• La deformazione plastica delle piastre è del 15 %

La stima della capacità di rotazione è importante nelle connessioni esposte a rischio sismico, si vedano Gioncu e Mazzolani (2002) e Grecea (2004), e a carichi estremi, si veda Sherbourne e Bahaari (1994 e 1996). La capacità di deformazione dei componenti è stata studiata a partire dalla fine del secolo scorso (Foley e Vinnakota, 1995). Faella et al. (2000) hanno effettuato delle prove su elementi a T e hanno ricavato le espressioni analitiche per la capacità di deformazione. Kuhlmann e Kuhnemund (2000) hanno eseguito prove sull'anima di un pilastro sottoposto a compressione trasversale a diversi livelli di forza assiale di compressione nel pilastro. Da Silva et al. (2002) hanno previsto la capacità di deformazione a diversi livelli di forza assiale nella trave collegata. Sulla base dei risultati dei test combinati con l'analisi FE, sono state stabilite le capacità di deformazione dei componenti di base nei modelli analitici di Beg et al. (2004). In questo lavoro, i componenti sono rappresentati da spirali non lineari e opportunamente combinati per determinare la capacità di rotazione del giunto per le connessioni delle piastra di estremità, con piastra di estremità estesa o a filo e connessioni saldate. Per queste connessioni, i componenti più importanti che possono contribuire in modo significativo alla capacità di rotazione sono stati riconosciuti come l'anima in compressione, l'anima del pilastro in trazione, l'anima del pilastro in taglio, la flangia del pilastro in flessione e la piastra di estremità in flessione. I componenti relativi all'anima del pilastro sono rilevanti solo quando non ci sono irrigidimenti nel pilastro che resistono alle forze di compressione, trazione o taglio. La presenza di un irrigidimento elimina il componente corrispondente e il suo contributo alla capacità di rotazione del giunto può quindi essere trascurato. Le piastre di estremità e le flange del pilastro sono importanti solo per le connessioni delle piastre di estremità in cui i componenti agiscono come elementi a T, dove è inclusa anche la capacità di deformazione dei bulloni in tensione. Le questioni e i limiti della capacità di deformazione delle connessioni in acciaio ad alta resistenza sono stati studiati da Girao et al. (2004).

Progettazione in capacità della connessione in acciaio

La progettazione in capacità (gerarchia delle resistenze) è una parte della progettazione antisismica e della verifica del giunto. Laddove si fa affidamento sulla duttilità di una struttura, è necessario eseguire la gerarchia delle resistenze. 

L'obiettivo della gerarchia delle resistenze è quello di confermare che un edificio abbia un comportamento duttile controllato per evitare un collasso in caso di terremoto di livello progettuale.

Viene selezionata una struttura dissipativa con una maggiore resistenza e un diagramma dei materiali modificato. Vengono definiti un fattore di sovraresistenza (\gamma_{ov}\) in Materiali e un fattore di incrudimento \(\gamma_{sh}\)al funzionamento della struttura dissipativa. Si noti che la nomenclatura differisce tra i codici. Un elemento dissipativo è escluso dalla verifica di sollecitazione delle piastre. 

Diagramma di materiale modificato per l'elemento dissipativo

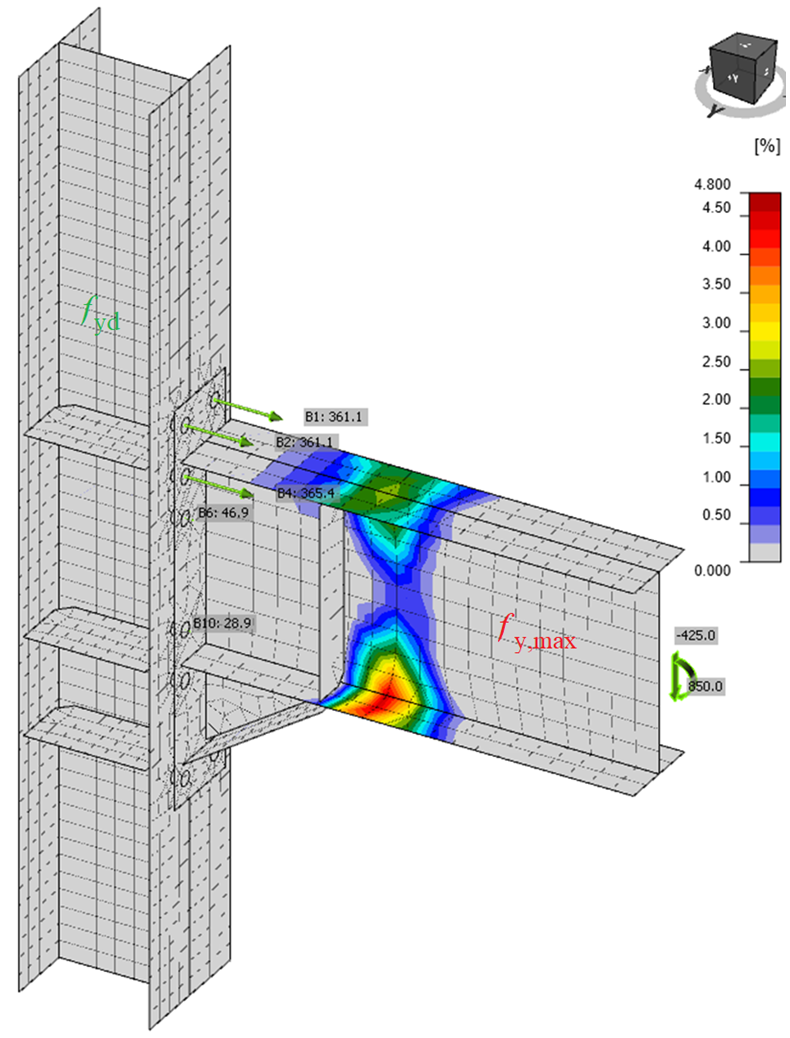
IDEA StatiCa Connection verifica la connessione sulla base del carico di progetto applicato, che dovrebbe creare una cerniera plastica nella struttura dissipativa selezionata, di solito la trave. La deformazione plastica della struttura dissipativa deve essere del 5% circa. Ciò può servire a confermare che l'entità e la posizione dei carichi sono state determinate correttamente. 

La cerniera plastica si verifica nel punto previsto dell'elemento dissipativo: la trave

I vincoli dell'elemento continuo sono automaticamente definiti con supporto a un'estremità e con momenti limitati all'altra estremità. In questo modo, il pilastro continuo può essere sottoposto a forza normale e a forze di taglio, e inoltre un lato può spostarsi lateralmente in modo da rivelare il cedimento dell'anima del pilastro a taglio.

Si noti che i dettagli sono molto importanti per i giunti antisismici, ma non sono verificati in IDEA StatiCa. 

Resistenza di progetto della connessione in acciaio

Il progettista, di solito, progetta la connessione/giunto per trasferire il carico di progetto noto. Tuttavia, è utile sapere anche quanto il progetto sia lontano dallo stato limite, cioè a quanto ammonti la riserva nel progetto e quanto sia sicura. È possibile fare ciò semplicemente tramite l’analisi Resistenza di progetto dell'unione.

L'utente inserisce il carico di progetto come in un progetto standard. Il software aumenta automaticamente tutti i componenti di carico in modo proporzionale, fino a quando non sia soddisfatta una delle verifiche previste. 

Le analisi di resistenza di progetto effettuano verifiche sui seguenti componenti:

• Deformazione plastica nelle piastre
• Bulloni: taglio, trazione e una combinazione di trazione e taglio
• Ancoraggi: resistenza a trazione e taglio dell'acciaio 
• Saldature

Si noti che altri componenti non inclusi nell'elenco precedente non saranno verificati poiché le direzioni delle forze in tali componenti sono sconosciute. Per questo motivo, è necessario effettuare sempre un'analisi EPS per verificare che tutti i controlli siano stati eseguiti correttamente. 

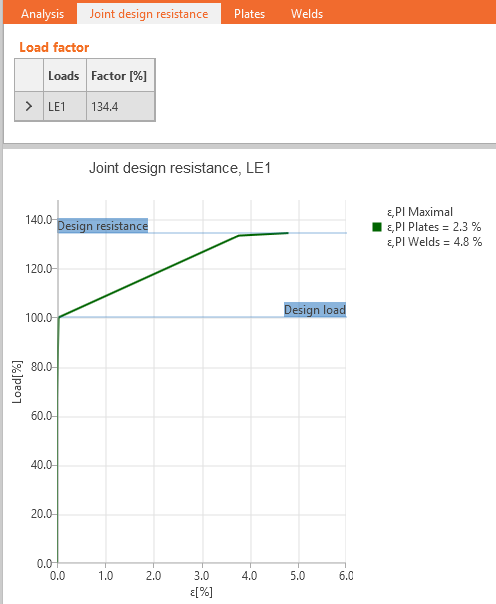
L'utente ottiene il rapporto tra il carico massimo e il carico di progetto. Inoltre, viene fornito un diagramma semplice. 

Sono mostrati i risultati dei casi di carico definiti dall'utente, a meno che il fattore di resistenza di progetto del giunto non sia inferiore al 100%, il che significa che il calcolo non è convergente, e viene mostrata l'ultima fase di convergenza del caso di carico.

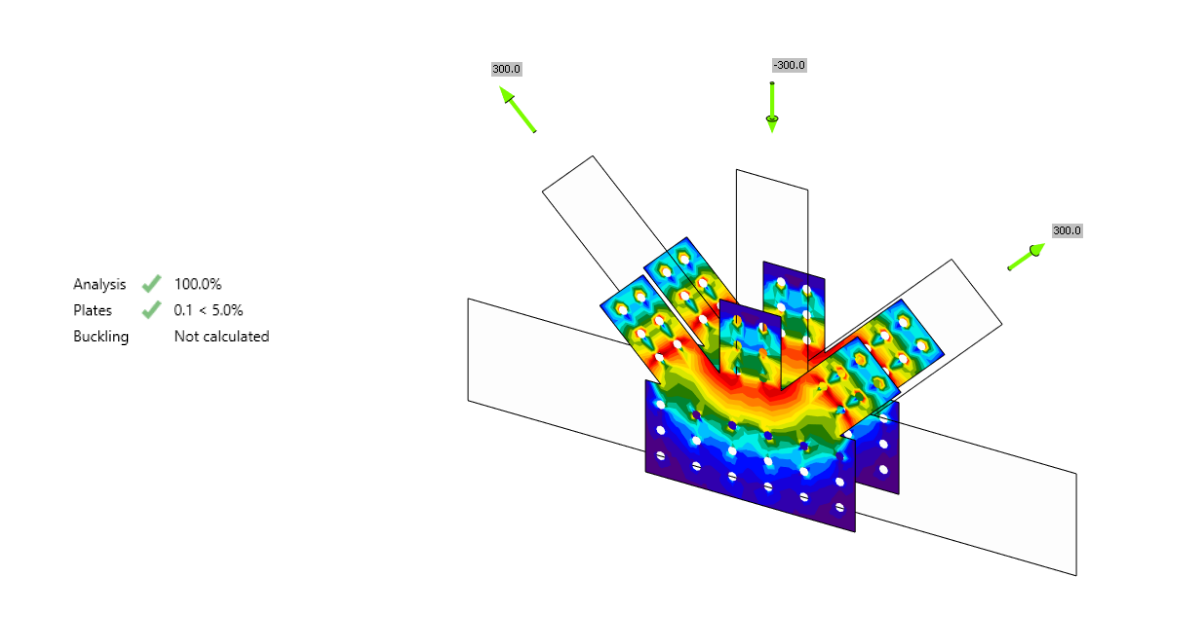
Analisi di instabilità dei giunti in acciaio

Solitamente, nei giunti, l'instabilità non è un problema rilevante. Tuttavia, è necessario verificare che non vi siano problemi di instabilità e che i risultati dell'analisi di resistenza, che si avvale solo dell'analisi lineare per geometria, siano corretti.

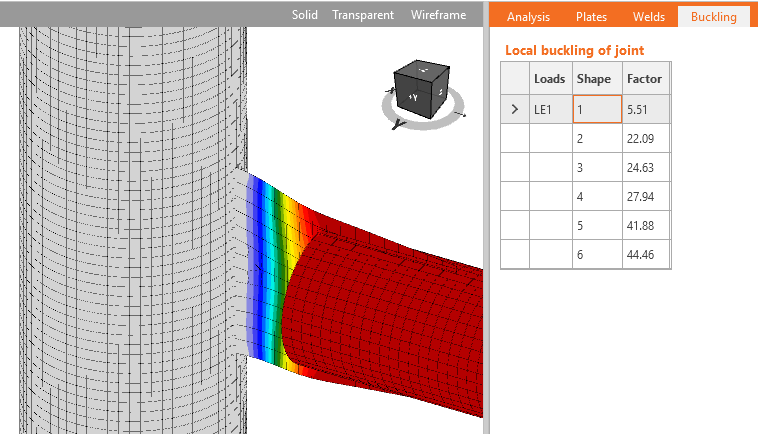
IDEA StatiCa Connection può eseguire l'analisi di instabilità lineare di un modello di giunto. I risultati sono predetti dalle modalità di instabilità. Per ogni modalità di instabilità viene calcolato il carico critico, al quale si verifica l'instabilità del modello perfetto. Il carico critico è presentato da moltiplicatori del carico che agiscono sul giunto. In base alla modalità di instabilità e al moltiplicatore del carico critico, l'utente è in grado determinare la progettazione di instabilità sicura.

Alcuni codici, ad esempio l'Eurocodice (EN 1993-1-1, capitolo 5.2.1), raccomandano un moltiplicatore di carico critico superiore a 15 per i modelli di strutture a barre. Se il moltiplicatore del carico critico è superiore a 15, il codice non richiede una verifica di instabilità delle membrature.

Per i giunti, la questione è diversa e il codice non fornisce alcuna raccomandazione specifica. La progettazione dell'instabilità locale deve essere affrontata in un altro modo. In generale, l'instabilità locale può essere suddivisa in tre gruppi:

1. Piastre che collegano le singole membrature
2. Piastre di irrigidimento nel giunto: irrigidimenti, nervature, fazzoletti d’angolo corti
3. Sezioni chiuse e sezioni a parete sottile

L'instabilità delle piastre del gruppo 1 influisce sulla forma di instabilità dell'intera struttura. Pertanto, si raccomanda di applicare anche a queste piastre le stesse regole applicate a queste membrature, ossia di considerare un moltiplicatore di carico critico sicuro pari a 15 o superiore. L'ingegnere deve verificare che l'esecuzione reale del giunto corrisponda alle condizioni limite del modello utilizzato per l'analisi di instabilità dell'intera struttura.

Le piastre del gruppo 2 influiscono sull'instabilità locale del giunto. Per tali piastre, il limite di sicurezza del moltiplicatore di carico critico 15 è conservativo, ma mancano indicazioni specifiche nei codici. La guida è fornita da pubblicazioni di ricerca che raccomandano un limite di sicurezza di moltiplicatore di carico critico pari a 3.

L'instabilità di piastre e membrature del gruppo 3 è molto problematica ed è necessaria una valutazione singola di ogni caso particolare.

Per le piastre con un moltiplicatore di carico critico inferiore ai valori suggeriti (15 per il gruppo 1, 3 per il gruppo 2), non è possibile utilizzare la progettazione plastica. Per il loro controllo, sono necessari altri metodi non offerti da IDEA StatiCa.

Il risultato dell'analisi di instabilità in IDEA StatiCa Connection non è una verifica definitiva. I codici non forniscono indicazioni sufficienti. La valutazione richiede un giudizio ingegneristico e IDEA StatiCa fornisce strumenti unici non disponibili nei software di progettazione standard.

Piastra a fazzoletto come allungamento di una travatura reticolare: esempio di piastra del gruppo 1 per la quale l'instabilità può essere trascurata se il fattore di instabilità critico è superiore a 15

Esempi di forme di instabilità di piastre del gruppo 2 in cui l'instabilità può essere trascurata se il fattore di instabilità critico è superiore a 3

Il modello utilizzato per l'analisi di instabilità è sostenuto da supporti diversi rispetto a quelli impostati dall'utente nell’analisi delle sforzo e deformazione (EPS). L'elemento resistente è completamente vincolato. Il tipo di modello di una trave impostato come N-Vy-Vz-Mx-My-Mz (libero di muoversi nell’analisi delle sollecitazioni e delle deformazioni) è completamente vincolato nell'analisi di instabilità. Tutte le altre analisi della trave hanno momenti flettenti e forza normale limitati, ma sono liberi di muoversi lateralmente.

• Modello N-Vy-Vz-Mx-My-Mz: supporti nel modello di instabilità: N-Vy-Vz-Mx-My-Mz
• Modello N-Vy-Vz: supporti nel modello di instabilità: N-Mx-My-Mz
• Modello N-Vz-My: supporti nel modello di instabilità: N-Mx-My-Mz
• Modello N-Vy-Mz: supporti nel modello di instabilità: N-Mx-My-Mz

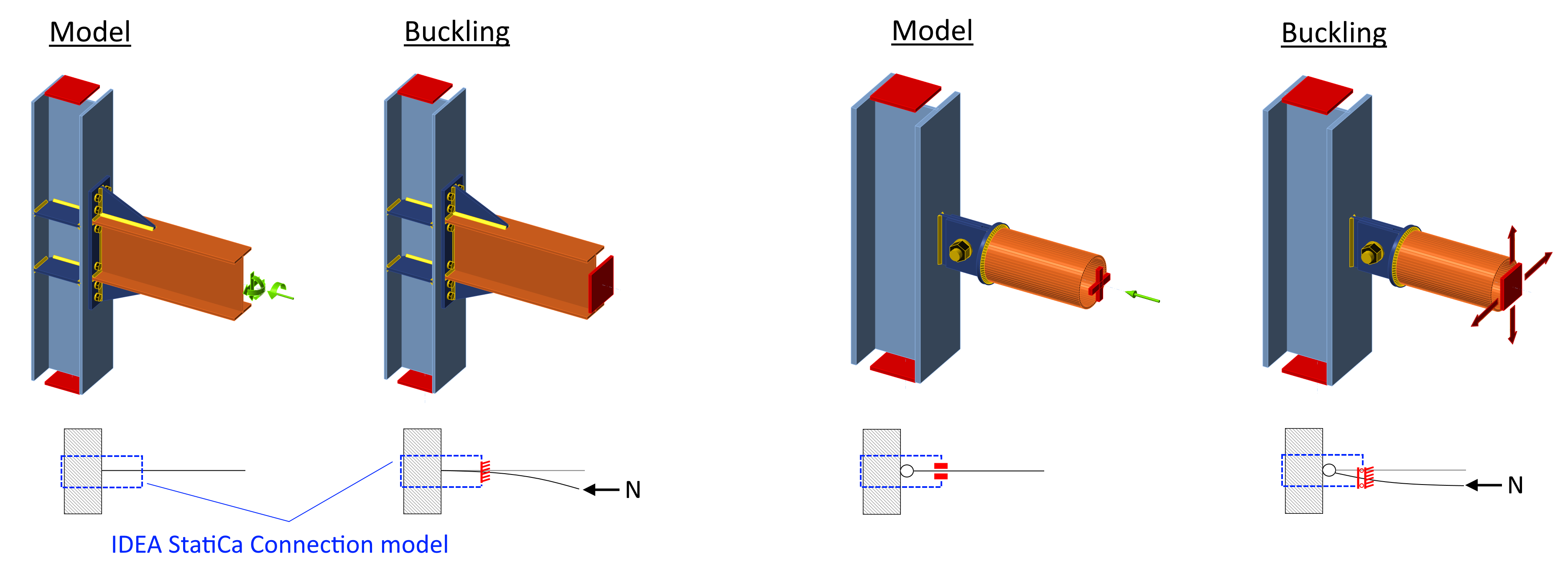
Si assume che, in caso di giunto rigido, l'utente imposti il momento flettente e che l'instabilità del segmento corto della trave non sia rilevante. Diversamente, nel caso di un giunto a cerniera, l'utente imposta solo la forza normale e di taglio e non il momento flettente, ma l'instabilità dell'elemento a cerniera è rilevante e contribuisce al fattore di instabilità. Si veda la figura seguente. "Model" mostra il modello nell’analisi sforzo-deformazione, mentre "Buckling" mostra il modello nell'analisi di instabilità.

Convergenza dell'analisi di modelli complessi di connessioni in acciaio

L'analisi agli elementi finiti potrebbe non convergere per diversi motivi, di solito a causa di qualche elemento che non ha sufficienti supporti e può muoversi o ruotare liberamente.

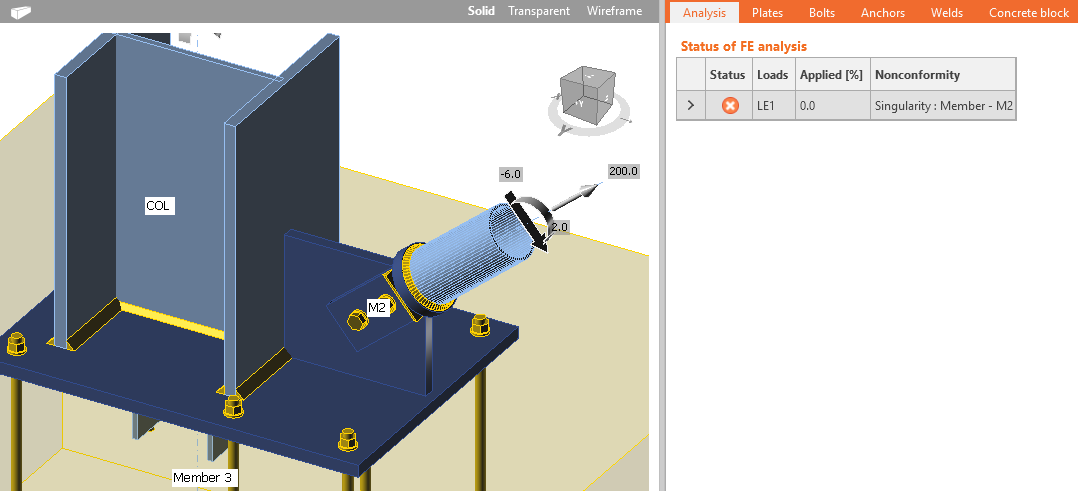
L'analisi agli elementi finiti richiede un diagramma sforzo-deformazione leggermente crescente dei modelli di materiale. In alcuni casi di modelli complicati, ad esempio con contatti multipli, l'aumento delle iterazioni divergenti potrebbe contribuire alla convergenza. Questo valore può essere impostato in Impostazione codice. Le cause più comuni di fallimento dell'analisi sono le singolarità in cui le parti di un modello non sono collegate correttamente e sono libere di muoversi o ruotare. L'utente riceve una notifica e deve verificare che il modello non presenti saldature o bulloni mancanti. La forma alterata viene mostrata con gli elementi che hanno causato la prima singolarità spostati di 1 m, in modo che tale singolarità possa essere facilmente individuata.

Saldature mancanti sulle piastre a fazzoletto con conseguente singolarità 

Giunti acciaio-legno

I giunti acciaio-legno sono presenti al momento solo per la verifica delle piastre in acciaio e la determinazione dei vettori di forza negli elementi di fissaggio. Le piastre del fazzoletto possono essere applicate sia racchiuse che inserite.

Le proprietà del materiale del legno non sono specificate. Le verifiche degli elementi di fissaggio e del legno devono essere eseguite manualmente o con un altro software secondo le regole di progettazione appropriate. Pertanto, l'analisi di rigidezza non è disponibile. 

La verifica di tutti gli altri componenti delle connessioni in acciaio è effettuata come di consueto.

Per saperne di più su come lavorare con i giunti acciaio-legno, consulta l’articolo sulle conoscenze di base. 

Membrature in acciaio a parete sottile

L’uso di IDEA StatiCa Connection per la progettazione di giunti di elementi a parete sottile è da affidare solamente a ingegneri esperti. L'analisi di instabilità è indispensabile e ogni forma di modalità deve essere analizzata attentamente.

Il software IDEA StatiCa Connection è dedicato alla valutazione delle connessioni di elementi laminati a caldo che non sono significativamente affetti da instabilità. Grazie al calcolo veloce e stabile, viene eseguita l'analisi lineare per geometria e non lineare per materiale. Tuttavia, tale analisi non è sufficiente per la perdita di stabilità. Se l'instabilità può essere un problema, lo svolgimento di un'analisi di instabilità lineare aiuta a individuare le aree a rischio e a fornire un fattore per il punto di biforcazione di Eulero, ma ciò non è ancora sufficiente per le membrature a parete sottile. Per le membrature a parete sottile, è adatta solo l'analisi non lineare per geometria con imperfezioni.

Se l'utente decide comunque di utilizzare il software IDEA StatiCa Connection per verificare le connessioni di elementi a parete sottile, deve:

• Eseguire l'analisi di instabilità lineare e valutare attentamente ogni forma di instabilità, le prime 5 forme di instabilità presentate potrebbero non essere sufficienti (Come aumentare il numero delle forme valutate)
• Non fare affidamento sulla plasticità delle piastre in acciaio e limitare piuttosto la sollecitazione di von Mises alla resistenza limite o anche inferiore
• Tenere presente che l'instabilità locale, che non viene considerata, può ridistribuire le forze interne nei componenti in modo diverso
• Tenere presente che la rigidezza dei componenti può essere diversa per via delle diverse modalità di cedimento o della loro combinazione.
• Tenere presente che le verifiche presentate e i dettagli dei componenti (ad esempio, bulloni, saldature) sono le seguenti guide per gli elementi standard. Le verifiche per gli elementi a parete sottile possono variare e quindi le verifiche fornite non sono corrette.

La progettazione di connessioni di elementi a parete sottile è molto specifica e non è possibile fornire una guida generale. IDEA StatiCa Connection non è stata convalidata per questo uso.

Verifiche delle componenti – EN

Nella norma EN 1993-1-1 le membrature a parete sottile sono definite come segue: "Le sezioni trasversali di classe 4 sono quelle in cui si verifica un’instabilità locale prima del raggiungimento della resistenza limite in una o più parti della sezione trasversale". La parte principale di Eurocodice relativa all'acciaio si limita alle membrature con spessore del materiale t ≥ 3 mm. Il Capitolo 4 – Connessioni saldate si applica solo a uno spessore del materiale t ≥ 4 mm. Pertanto, le verifiche dei componenti fornite dal software non si applicano alle membrature formate a freddo con spessori inferiori. Gli utenti ne devono essere a conoscenza e devono sostituire manualmente le verifiche con le formule appropriate della EN 1993-1-3.

L’analisi di giunti a sezione cava deve essere eseguita con attenzione anche per le membrature che non rientrano nell'intervallo di validità dei giunti saldati - EN 1993-1-8 - Tabella 7.1. Non esistono linee guida per tali giunti e i risultati del software non sono stati convalidati.

Verifiche delle componenti – AISC

Nel capitolo A dell'AISC 360-16 si trova una nota per l'utente che afferma: "Per la progettazione di membrature strutturali in acciaio formate a freddo, si raccomanda l'applicazione delle disposizioni contenute nella specifica AISI North American Specification for the Design of Cold-Formed Steel Structural Members (AISI S100), ad eccezione dei profilati strutturali cavi formati a freddo (HSS), che sono progettati in conformità alla presente specifica." AISI S100 e AS/NZS 4600 forniscono delle formule per determinare la resistenza al taglio e alla trazione dei tipi di elementi di fissaggio più comuni, insieme al relativo campo di applicazione

Verifiche delle componenti – CISC

Il CSA S16-14, al capitolo 1, afferma: "I requisiti per le strutture in acciaio come ponti, tralicci, strutture offshore ed elementi strutturali in acciaio formati a freddo sono indicati in altre norme del Gruppo CSA"

Vincolo latero-torsionale nella progettazione strutturale

Descrizione del modello

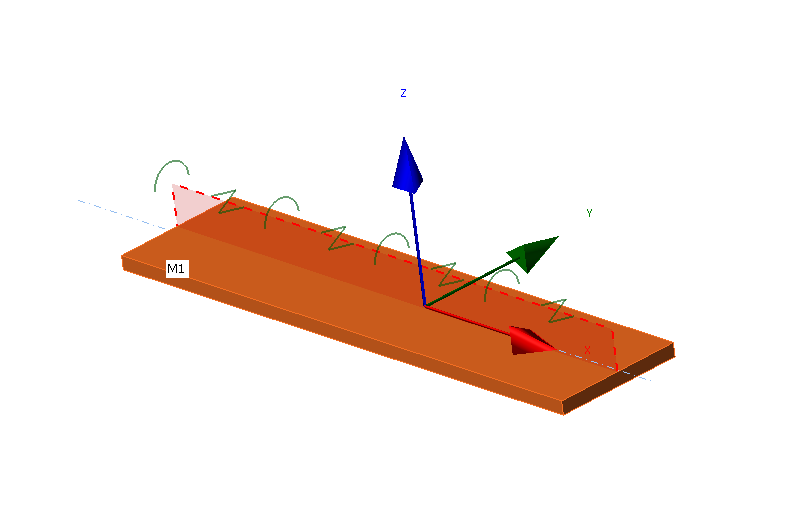
Il Vincolo latero-torsionale è simulato da due rigidezze aggiunte a qualsiasi piastra:

• Laterale (taglio) S [N] applicato in direzione dell'asse y del sistema di coordinate locali della piastra
• Torsionale C [Nm/m] applicata intorno all'asse x del sistema di coordinate locali della piastra

Gli utenti possono selezionare qualsiasi piastra di una membratura, la lunghezza del vincolo, il tipo (continuo o discreto con distanza impostata) e le rigidezze laterali e torsionali.

Sistema di coordinate locali di una piastra con LTR applicata

I nodi degli elementi finiti sono collegati lungo la larghezza della piastra da elementi di corpo rigido di tipo 3 (RBE3) a un punto dell'asse longitudinale della piastra. La rigidezza torsionale è applicata a questo punto da un elemento speciale a una sola rigidezza, la rotazione attorno all'asse x . Tale punto è collegato anche da altri due RBE3 con un elemento speciale tra loro a una rigidezza, lo spostamento sull'asse y . 

La rigidezza laterale può essere impostata dall'utente come libera, rigida o con rigidezza impostata. La rigidezza rigida è sufficientemente elevata, pari a 1000 volte la rigidezza a taglio della piastra. La rigidezza S è impostata per unità di lunghezza (un metro) con un'unità di forza [N]. La rigidezza di un elemento Si ha un'unità di forza divisa per l'unità di lunghezza [N/m] ed è quindi:

\[ S_i = \frac{S}{s_d} \]

dove:

•  \(s_d\) – distance between two points [m]

Per la tipologia discreta, la distanza viene impostata direttamente dall'utente. Per la tipologia continua, la distanza è sufficientemente piccola da non influenzare il comportamento della piastra.

Analogamente, la rigidezza torsionale è impostata dall'utente come libera, rigida o con rigidezza impostata. La rigidezza rigida è sufficientemente elevata, pari a 1000 volte la rigidezza flessionale della piastra. La rigidezza C è impostata per unità di lunghezza (un metro) con un'unità di misura del momento flettente diviso per l'unità di lunghezza [Nm/m]. La rigidezza di un elemento Ci ha un’unità di momento flettente diviso per l'unità di lunghezza al quadrato [Nm/m²] ed è quindi:

\[ C_i = \frac{C}{s_d} \]

Per una migliore comprensione dei valori di rigidezza, consultare il documento Raccomandazioni europee sulla stabilizzazione di strutture in acciaio con pannelli sandwich.

Gli elementi finiti nascosti e l'RBE3 forniscono la rigidezza laterale e torsionale alla piastra della membratura

Si noti che gli RBE3 sono solo links di interpolazione che non forniscono alcuna rigidezza.

Verifica

Si è verificato, tramite il software LTBeam, che si avvale di elementi a barra (1D) con sette gradi di libertà, un modello che fornisce il vincolo LRT. Ciò significa che la sezione trasversale non è deformata, ma l'elemento può essere soggetto a warping.  Il confronto è mostrato su un esempio di sezione IPE 180 in acciaio S355 lunga 6 m. La trave è fissata ad entrambe le estremità con un carico uniforme di 20 kN/m applicato all'ala superiore. Il software LTBeam è in grado di determinare il momento elastico critico che corrisponde al risultato dell'analisi di instabilità lineare (LBA) in IDEA StatiCa Member.

Confronto tra LTBeam e IDEA StatiCa Member per la rigidezza laterale e torsionale 

Il moltiplicatore di carico critico per l'instabilità elastica α_cr con rigidezza laterale è molto simile secondo entrambi i software. La rigidezza laterale limite alla quale l'instabilità latero-torsionale ha un effetto fino a solo il 5% della resistenza a flessione della trave, è calcolata secondo la norma EN 1993-1-1 come S_lim = 8 589 kN. Tuttavia, i risultati con il vincolo torsionale divergono a livelli più elevati di rigidezza rotazionale. Osservando la forma deformata in IDEA StatiCa Member, la differenza deriva dalla deformazione della sezione trasversale, la quale può essere captata solo dal modello shell. LTBeam fornisce, per una rigidezza torsionale alta, moltiplicatori di carico critico irrealisticamente elevati. 

Per verificare questa affermazione, presso l'università ETH è stato creato il modello di elementi shell ABAQUS. Anche in questo caso la trave è fissata ad entrambe le estremità, è realizzata in acciaio S355 e ha una lunghezza di 6 m. È stata utilizzata la sezione trasversale di trave IPE 240. La rigidezza torsionale limite, cioè l'instabilità latero-torsionale che ha un effetto solo fino al 5% della resistenza a flessione della trave, è stata calcolata come C_lim = 27,13 kNm/m. Il modello è sottoposto a una forza a metà della campata in corrispondenza dell'ala superiore. 

Confronto tra ABAQUS, LTBeam e IDEA StatiCa Member per la rigidezza torsionale

L'effetto della rigidezza torsionale è molto simile in entrambi i modelli costituiti da elementi shell, mentre LTBeam diverge. Soprattutto, le resistenze all'instabilità di ABAQUS e  IDEA StatiCa Member fornite dalla GMNIA quasi coincidono (le differenze sono fino al 4%).

Stima della rigidezza

Il vincolo LTR dato da solai riempiti di calcestruzzo e con azione composta data da montanti a taglio (shear studs) può essere assunto come rigido, almeno per quanto riguarda la rigidezza laterale. Le rigidezza date dalle lastre trapezoidali dei pannelli sandwich sono molto minori e possono essere determinate mediante esperimenti o calcoli. Il più delle volte, i valori di rigidezza laterale e torsionale sono raccomandati dai produttori di pannelli sandwich o di altri tipi di rivestimento. 

Il calcolo della rigidezza laterale S [N] data dalle lastre trapezoidali è riportato nella norma EN 1993-1-3, capitolo 10:

\[S=1000 \sqrt{t^3} \left ( 50+10 \sqrt[3]{b_{roof}} \right ) \frac{s}{h_w} \]

dove:

• t – spessore di progetto della lastra trapezoidale [mm]
• b_roof – larghezza del tetto, ad esempio per un tetto spiovente, è la distanza tra il colmo e una gronda [mm]
• s – distanza tra le travi [mm]
• h_w – profondità del profilo della lastra trapezoidale [mm] 

La formula è valida se la lastra trapezoidale è collegata alla trave in corrispondenza di ogni nervatura. Se la lastra è collegata alla trave solo in corrispondenza di una nervatura ogni due, allora S deve essere sostituito da 0,2 S.

La rigidezza laterale dei pannelli sandwich è descritta nella raccomandazione ECCS. La rigidezza degli elementi di fissaggio è fondamentale:

\[S=\frac{k_v}{2B} \sum_{k=1}^{n_k}c_k^2\]

dove:

• k_v – rigidezza a taglio di un elemento di fissaggio
• B - larghezza del pannello sandwich
• n_k - numero di coppie di elementi di fissaggio per pannello e supporto
• c_k - distanza tra i due elementi di fissaggio di una coppia

La rigidezza torsionale è più complessa e può essere stimata anche in base alle raccomandazioni ECCS. Contiene il contributo degli elementi di fissaggio, del pannello sandwich e della distorsione della trave. La distorsione della trave può essere trascurata perché è già inclusa nel modello degli elementi shell.

Rigidezza torsionale (a sinistra) e laterale (a destra) fornita dai pannelli sandwich (ECCS, 2014)

Nella pratica americana, il contenimento contro l'instabilità latero-torsionale è tipicamente assunto come totale o trascurabile in base al tipo e all'orientamento dell'impalcato. Ad esempio, la Tabella 8.1 del Manuale di progetto sismica AISC identifica le condizioni di vincolo per le travi soggette a compressione assiale. Tuttavia, se necessario, la rigidezza laterale può essere derivata dalla rigidezza del diaframma, G', calcolata secondo la norma AISI S310. Denavit et al. (2020) presentano un metodo di calcolo della rigidezza torsionale. 

Riferimenti

• CTICM, LTBeam v. 1.0.11, available at: https://www.cesdb.com/ltbeam.html
• Abaqus. Reference manual, versione 6.16. Simulia, Dassault Systéms. Francia, 2016.
• EN 1993-1-3: Eurocodice 3: Progettazione di strutture in acciaio - Parte 1-3: Norme generali - Norme supplementari per membrature e lamiere formate a freddo, CEN, 2006.
• ECCS TC7 - Technical Working Group TWG 7.9 Sandwich Panels and Related Structures, European Recommendations on the Stabilization of Steel Structures by Sandwich Panels, 2^a edizione, 2014. ISBN 978-90-6363-081-2
• Denavit, M.D.; Jacobs, W.P.; Helwig, T.A. (2020). "Continuous Bracing Requirements for Constrained-Axis Torsional Buckling," Engineering Journal, American Institute of Steel Construction, Vol. 57, pag. 69-89.

Giunti in acciaio di membrature a sezione cava

I giunti di membrature a sezione cava possono subire gravi deformazioni pur essendo in grado di sopportare carichi più elevati degli attuali. Dall’altro lato, le piastre possono deformarsi in un campo anelastico, perciò viene eseguita un'analisi non lineare per geometria e per materiale.

Deformazione fuori piano

Uno dei criteri per lo stato limite ultimo dei giunti a sezione cava è la deformazione fuori piano della sezione trasversale della sezione cava. Tale verifica è disponibile nel software (in Impostazione codice denominata Verifica delle deformazioni locali, attivata per impostazione predefinita nel caso membratura resistente con sezione cava). È riconosciuta dalle Guide di progettazione CIDECT. I limiti sono pari al 3% della dimensione minore della sezione trasversale (0,03 d₀ per CHS e 0,03 b₀ per RHS) per lo stato limite ultimo e all'1% per lo stato limite di esercizio.

Definizione delle dimensioni di sezione trasversale per sezione cava circolare (CHS) e sezione cava rettangolare (RHS)

Tipici diagrammi sforzo-deformazione per giunti a sezione cava; la curva rossa è relativa all'elemento a parete sottile sottoposto a compressione, la curva verde agli elementi regolari sottoposti a compressione, la curva blu è riferita al giunto a X sottoposto a trazione

Analisi non lineare per geometria e per materiale (GMNA)

Nel caso di alcuni giunti di sezioni cave, soprattutto con un rapporto diametro/spessore elevato, l'analisi lineare per geometria potrebbe non cogliere il comportamento del giunto con sufficiente precisione e la resistenza al carico potrebbe essere sotto o sovrastimata. Si raccomanda di utilizzare analisi non lineari per geometria e per materiale più avanzate per i giunti di sezioni cave, anche se il tempo di calcolo è leggermente superiore. Se in Impostazione codice è selezionata per le sezioni cave l'analisi GMNA, viene utilizzata tale analisi per i modelli con una membratura a sezione cava definito come elemento portante, invece dell'analisi lineare per geometria e non lineare per materiale (MNA, utilizzata come standard in IDEA Statica Connection).

Nota: Se l'elemento resistente non è a sezione cava, la soluzione GMNA è disabilitata per l'analisi dell'intero modello della connessione, indipendentemente dalla Impostazione del codice (GMNA on od off).

La sezione si deforma all'estremità del modello shell

La sezione trasversale può deformarsi alle estremità del modello costituito da elementi shell. I giunti di sezioni cave richiedono membrature relativamente lunghe, fino a 10 volte il diametro della sezione trasversale. Il super-elemento condensato è posto dietro la parte di modello costituita da elementi shell. Ciò consente un calcolo più rapido con la stessa precisione del modello completo costituito da elementi shell. Il super-elemento condensato ha solo proprietà materiali elastiche, e ciò significa che le deformazioni plastiche dovute alla modalità di cedimento studiata non dovrebbero raggiungere l’estremità del modello dell'elemento shell. Per questo motivo, il modello shell si estende per default per 1,25 volte l'altezza della sezione trasversale (modificabile in Impostazione codice), dietro l'ultima operazione di produzione.  

Resistenza a flessione dello shell ridotta per le sezioni cave (imperfezioni)

Nei codici, le resistenze al carico dei giunti di sezioni cave sono determinate dal Failure Mode Method, che si avvale di modelli di curve-fitting determinati da esperimenti e modelli numerici avanzati. La struttura reale contiene imperfezioni iniziali e sollecitazioni residue, che non sono registrate dai modelli shell in IDEA StatiCa Connection. Per una maggiore conformità ai risultati dei codici, l'influenza delle sollecitazioni residue e delle imperfezioni iniziali viene simulata riducendo la resistenza a flessione delle membrane (shell) di sezioni cave con un rapporto D/(2t) elevato.

Analisi a fatica nella progettazione strutturale

L’analisi a fatica non fornisce alcuna resistenza finale o numero di cicli che il dettaglio può sopportare. Fornisce solamente degli spunti per ulteriori calcoli in base ai codici.

È sempre necessario impostare almeno due casi di carico. Il primo caso di carico è quello di riferimento. Si assume, ad esempio, un peso proprio della struttura e può contenere carichi nulli. Gli altri casi di carico simulano le azioni di fatica. Lo sforzo nominale normale e di taglio fornito da IDEA StatiCa è l'intervallo di sforzo tra l'azione di fatica, ad esempio LE2, e il caso di carico di riferimento.

Ad esempio, lo sforzo di taglio in un determinato punto è di 50 MPa nel caso di carico di riferimento e di 180 MPa in LE2. Lo sforzo di taglio nominale indicato in questo punto è:

\[\tau = 180-50=130\, \textrm{MPa}\]

Si noti che non deve verificarsi alcuno snervamento delle piastre determinato delle azioni di fatica, altrimenti gli intervalli di sforzo vengono distorti. 

Le sollecitazioni sono disponibili per:

• Bulloni
• Saldature
• Piastre

Bulloni

In corrispondenza dei bulloni, le sollecitazioni sono determinate semplicemente dividendo la forza per l'area corrispondente:

• \(\sigma = F_t / A_s \)
• \(\tau = V / A \)

dove:

• \(F_t\) – forza di trazione nel bullone
• \(A_s\) – area del bullone sollecitata a trazione 
• \(V\) – forza di taglio nel bullone; nel caso di più piani di taglio, si utilizza la forza di taglio più alta
• \(A\) – area del bullone resistente a taglio; area di sollecitazione a trazione se le filettature sono intercettate dal piano di taglio, altrimenti, area della sezione trasversale lorda

Saldature

Le saldature in CBFEM sono costituite dall'elemento di saldatura a vincoli multipli che collega le piastre. La distribuzione delle sollecitazioni nella saldatura è disturbata dai vincoli e, pertanto, le sollecitazioni sono considerate da una sezione situata a 1,5 volte la lunghezza del cordone dal punto iniziale. Vengono create tre sezioni per una saldatura ad angolo bilaterale. Due sezioni appartengono alla stessa categoria di dettaglio e viene mostrata solo quella più sollecitata. Sono mostrati lo sforzo normale massimo e lo sforzo di taglio corrispondente nello stesso punto, nonché lo sforzo di taglio massimo e lo sforzo normale corrispondente nello stesso punto.

Si vedano anche i miglioramenti dell'analisi a fatica nella versione 22.0.

Piastre

È possibile visualizzare le sollecitazioni nelle piastre creando una sezione definita dall'utente tramite un'operazione di produzione del piano di lavoro. Nella figura seguente sono stati creati due piani di lavoro per visualizzare le sollecitazioni intorno ai fori dei bulloni. Sono mostrati lo sforzo normale massimo e lo sforzo di taglio corrispondente nello stesso punto, nonché lo sforzo di taglio massimo e lo sforzo normale corrispondente nello stesso punto.

Progettazione in caso di incendio

Temperatura

In IDEA StatiCa Member, l'utente imposta una temperatura per l'intero modello. Tutte le entità del modello hanno una temperatura impostata.

In IDEA StatiCa Connection, l'utente può impostare la temperatura per ogni membratura o piastra separatamente. La temperatura degli elementi di collegamento (bulloni e saldature) viene assunta in base alla piastra di collegamento più calda.

La temperatura di elementi e piastre nelle connessioni può essere determinata secondo la norma EN 1993-1-2 - Cl. 4.2.5 Steel temperature development [Sviluppo della temperatura dell'acciaio] e D.3 Temperature of joints in fire [Temperatura dei giunti in caso di incendio].

Degrado del materiale

Il degrado del materiale delle piastre d'acciaio è disponibile secondo tre codici:

• EN 1993-1-2 - Tabella 3.1
• AISC 360-16 - Tabella A-4.2.1
• CSA S16-14 - Tabella K.1

Per le piastre d'acciaio a sei punti, viene utilizzato il diagramma di materiale multilineare secondo la norma EN 1993-1-2 - Figura 3.1. Viene mostrato un esempio per l'acciaio S355, degradazione del materiale secondo EN 1993-1-2 - Tabella 3.1, e temperatura \(\theta = 560^{\circ}\textrm{C}\). L’inclinazione del ramo plastico oltre la resistenza limite \(f_y\) is \(E_{a,\theta}/1000\). I fattori di riduzione per il modulo di elasticità \(k_{E,\theta}\), per il limite di proporzionalità \(k_{p,\theta}\),e la resistenza limite \(k_{y,\theta}\) sono rispettivamente 0,426, 0,252 e 0,594. Si assume che la deformazione plastica si accumuli a partire dal limite di proporzionalità.

	Deformazione	Deformazione plastica	Tensione
	\(\varepsilon\) [%]	\(\varepsilon_{pl}\) [%]	\(\sigma\) [MPa]
0	0.00	0.00	0.0
1	0.10	0.00	89.5
2	0.25	0.15	131.4
3	0.50	0.40	160.5
4	1.00	0.90	191.3
5	2.00	1.90	210.9
6	15.00	14.90	222.5

Il degrado del materiale dei bulloni è disponibile secondo tre codici:

• EN 1993-1-2 - Tabella D.1
• AISC 360-16 - Tabella A-4.2.3
• CSA S16-14 - Tabella K.3

Il degrado  del materiale delle saldature è disponibile secondo un codice:

• EN 1993-1-2 - Tabella D.1

Solo la resistenza di bulloni e saldature si riduce. La loro rigidezza rimane invariata rispetto alla temperatura ambiente.

L'espansione termica è trascurata e non viene assunta in nessun modello. Se necessario, gli effetti dell'espansione termica devono essere simulati con carichi aggiuntivi.

Verifiche

Per impostazione predefinita, le piastre in acciaio sono verificate per deformazione plastica del 5%. 

Nell'Eurocodice è utilizzato, per le verifiche di bulloni e saldature, un fattore di sicurezza parziale dedicato alla resistenza di progetto al fuoco,\(\gamma_{M,fi}\). In tutti gli altri codici, vengono utilizzati i fattori di resistenza o di sicurezza standard. Le curve di carico-deformazione e le verifiche di bulloni e saldature sono ridotte dei fattori \(k_b\) e \(k_f\) in base alla temperatura impostata.

Si presume che i bulloni precaricati scorrano, ma sono verificati come normali bulloni completamente serrati.

La temperatura del blocco di calcestruzzo e degli ancoraggi non è nota e i componenti corrispondenti non sono verificati nella progettazione al fuoco.

Rigidezza

L'analisi di rigidezza non è attualmente disponibile per la resistenza di progetto al fuoco. Si raccomanda di utilizzare l'analisi di rigidezza per la temperatura ambiente e di moltiplicare la rigidezza per il fattore di riduzione del modulo di elasticità \(k_{E,\theta}\).

Dimensionamento delle saldature

Le saldature sono le più costose e le più rilevanti nelle connessioni in acciaio. Una progettazione insufficiente può determinare cedimenti fragili, mentre una progettazione eccessiva un ritiro eccessivo. Il dimensionamento automatico delle saldature è volto a una progettazione rapida, coerente e sicura delle connessioni in acciaio.

In IDEA StatiCa Connection sono disponibili per tutti gli utenti due strategie di dimensionamento delle saldature:

• a resistenza massima
• oltre resistenza

Per gli utenti dell'Eurocodice, ve ne sono altri due:

• alla stima della capacità
• alla duttilità minima

Il metodo di dimensionamento della saldatura è specificato nella finestra di dialogo Operazioni.

Quando si esegue il dimensionamento, ogni saldatura riempita nel modello viene modificata in base al metodo di dimensionamento delle saldature. In genere, le dimensioni delle saldature aumentano in quest'ordine:

1. Alla stima della capacità
2. Alla duttilità minima
3. Alla resistenza massima
4. Con sovra-resistenza

I metodi sono descritti in dettaglio di seguito. 

Alla stima della capacità

Il dimensionamento delle saldature in base alla stima della capacità fornisce automaticamente dimensioni di saldatura sufficienti a consentire il trasferimento dei carichi impostati. 

La stima della capacità di saldatura è il primo utilizzo dell'apprendimento automatico (machine learning) in IDEA StatiCa. Al momento è implementato solo nell'Eurocodice. La resistenza di saldatura viene determinata in base all'elemento di saldatura più sollecitato. Pertanto, l'utilizzo della saldatura è altamente non lineare. La resistenza dell'intera lunghezza è stimata da un algoritmo di machine-learning basato sulla distribuzione delle tensioni lungo la lunghezza della saldatura.

Il dimensionamento delle saldature alla stima della capacità richiede risultati. La dimensione delle saldature a corodone d'angolo viene regolata in base alla seguente formula:

\[ a_{new} = a \cdot Ut_c / Ut_{target} \]

dove:

• \(a_{new}\) – dimensione della saldatura a cordone d'angolo regolata
• \(a\) – dimensione della saldatura a cordone d'angolo precedentemente impostata
• \(Ut_c\) – stima della capacità basata su un algoritmo di machine-learning visibile in Verifica saldature 
• \(Ut_{target}\) – utilizzo del target in Impostazioni → Progettazione → Autoprogetto → Dimensionamento delle saldature

Il risultato \(a_{new}\) viene arrotondato in base a Preferenze → Unità di applicazione → Arrotondamento nuova entità → Dimensione saldatura.

Si noti che le dimensioni della saldatura sono limitate dalle regole di dettaglio, ad esempio non possono essere inferiori a 3 mm (EN 1993-1-8 - 4.5.2). Queste regole di dettaglio sono rispettate. Inoltre, si tenga presente che le saldature multiple in IDEA StatiCa sono spesso impostate da un unico valore. In questi casi, la dimensione viene impostata in base a quella più utilizzata.

Inoltre, è disponibile un loop di calcolo. Quando il metodo di dimensionamento della saldatura è impostato su stima della capacità, si verifica quanto segue:

1. Dimensionamento delle saldature a cordone d'angolo alla massima resistenza
2. Calcolo del modello
3. Dimensionamento delle saldature a cordone d'angolo alla stima della capacità
4. Calcolo del modello

Le saldature vengono quindi impostate con un solo clic al livello di utilizzo desiderato o al di sotto di esso.

Alla duttilità minima

Il dimensionamento delle saldature in base alla duttilità minima fornisce automaticamente connessioni saldate sufficientemente robuste da evitare cedimenti fragili. La resistenza della saldatura consente la resistenza limite iniziale della piastra, ma alla fine la saldatura si rompe.

Il requisito di duttilità minima dei giunti saldati in FprEN 1993-1-8:2023 - 6.9(4). deriva dall'appendice nazionale olandese della norma EN 1993-1-8, in cui il rapporto fisso tra la resistenza della saldatura e la resistenza della piastra è di 0,8. È incluso anche nei famosi Libri verdi del Regno Unito, in particolare nei capitoli C2 e C3. Tuttavia, il rapporto fisso è adatto solo per l'acciaio S355. Nell'Eurocodice di seconda generazione è stato esteso a tutti i tipi di acciaio.

Tale requisito è verificato per le saldature ad angolo bilaterali da:

\[a/t=\frac{\beta_w\gamma_{M2} f_y}{\sqrt{2} f_u \gamma_{M0} } \cdot \min \left \{1.0, 1.1\frac{f_y}{f_u} \right \}\]

dove:

• \(a\) – altezza di gola della saldatura
• \(t\) – spessore della piastra collegata lungo il bordo
• \(\beta_w\) –  fattore di correlazione della saldatura 
• \(\gamma_{M2}\) –  fattore di sicurezza per bulloni e saldature; modificabile in Impostazione codice
• \(f_y\) –  resistenza limite della piastra
• \(f_u\) – resistenza ultima della saldatura
• \(\gamma_{M0}\) – coefficiente di sicurezza per le piastre; modificabile in Impostazione codice

L'altezza di gola della saldatura a cordone d'angolo unilaterale è due volte superiore a quella della saldatura a cordone d'angolo bilaterale.

Si noti che il metodo è utile per le saldature con carico trasversale e funziona se la piastra è collegata per tutta la sua larghezza.

Alla massima resistenza

Il dimensionamento delle saldature alla massima resistenza consente di ottenere automaticamente saldature più resistenti della piastra collegata. Nel calcolo, si ipotizza che le piastre siano sottoposte a trazione e le saldature a carico trasversale, come nel caso peggiore per la resistenza e la duttilità delle saldature. Questa progettazione è utile per evitare cedimenti fragili delle saldature per carichi statici.

Questo approccio è incluso anche nei largamente diffusi Green Book del Regno Unito, in particolare nel capitolo C1.

\[a/t=\frac{\beta_w\gamma_{M2} f_y}{\sqrt{2} f_u \gamma_{M0} }\]

dove:

• \(a\) – altezza di gola della saldatura
• \(t\) – spessore della piastra collegata lungo il bordo
• \(\beta_w\) – fattore di correlazione della saldatura 
• \(\gamma_{M2}\) – fattore di sicurezza per bulloni e saldature; modificabile in Impostazione codice
• \(f_y\) – resistenza limite della piastra
• \(f_u\) – resistenza ultima della saldatura
• \(\gamma_{M0}\) – coefficiente di sicurezza per le piastre; modificabile in Impostazione codice

Note that the method is useful for transversely loaded welds and works if the plate is connected by its full width.

Si noti che il metodo è utile per le saldature con carico trasversale e funziona se la piastra è collegata per tutta la sua larghezza.

In sovraresistenza

Il dimensionamento delle saldature in sovraresistenza consente di ottenere automaticamente saldature molto più resistenti della piastra collegata. Il fattore di sovraresistenza è specificato Impostazioni → Progetto→ Autoprogetto → Dimensionamento delle saldature. Il valore predefinito di 1,4 è tratto dalla norma EN 1993-1-8 - 6.2.3 (5) per formare una cerniera plastica. 

Nel calcolo, si ipotizza che le piastre siano sottoposte a trazione e le saldature a carico trasversale, come nel caso peggiore per la resistenza e la duttilità delle saldature. Questa progettazione è utile per evitare cedimenti fragili delle saldature in caso di progettazione plastica o di carico ciclico. Si noti che le grandi dimensioni della saldatura non garantiscono automaticamente un'elevata duttilità. Al contrario, possono comportare tensioni residue eccessive e deformazioni causate dal ritiro della saldatura.

Tale requisito è verificato per le saldature a cordone d'angolo bilaterali da:

\[a/t=\frac{\beta_w\gamma_{M2} f_y}{\sqrt{2} f_u \gamma_{M0} } \cdot f_{overstrength}\]

dove:

• \(a\) – altezza di gola della saldatura
• \(t\) – spessore della piastra collegata lungo il bordo
• \(\beta_w\) – fattore di correlazione della saldatura 
• \(\gamma_{M2}\) – fattore di sicurezza per bulloni e saldature; modificabile in Impostazione codice
• \(f_y\) – resistenza limite della piastra
• \(f_u\) –  resistenza ultima della saldatura
• \(\gamma_{M0}\) – fattore di sicurezza per le piastre; modificabile in Impostazione codice
• \(f_{overstrength}\) – fattore di sovraresistenza specificato in Impostazioni → Progetto → Autoprogetto→ Dimensionamento delle saldature

Si noti che il metodo è utile per le saldature con carico trasversale e funziona se la piastra è collegata per tutta la sua larghezza.