Verifikace únosnosti mostního deviátoru: IDEA StatiCa vs. ABAQUS simulace
U komorových mostů se pro změnu dráhy vnějšího předpětí používají deviátory. Jedná se o silně zatížený prvek a typickou D-oblast, kde se při špatném návrhu a analýze mohou vyskytnout vážné poruchy. V rámci příspěvku bude provedena analýza komorové mostní konstrukce s vnějším předpětím s detailním zaměřením na oblast deviátoru. Cílem je určit mezní únosnost deviátoru pokročilými numerickými metodami a simulovat stav napjatosti a deformace. Budou porovnány tři varianty řešení a jejich diverzita v únosnosti v souladu s předpoklady spolehlivostního přístupu, který je uveden v normách. Jednotlivé metody budou srovnány s cílem identifikovat nejefektivnější řešení dané úlohy.
Popis modelu
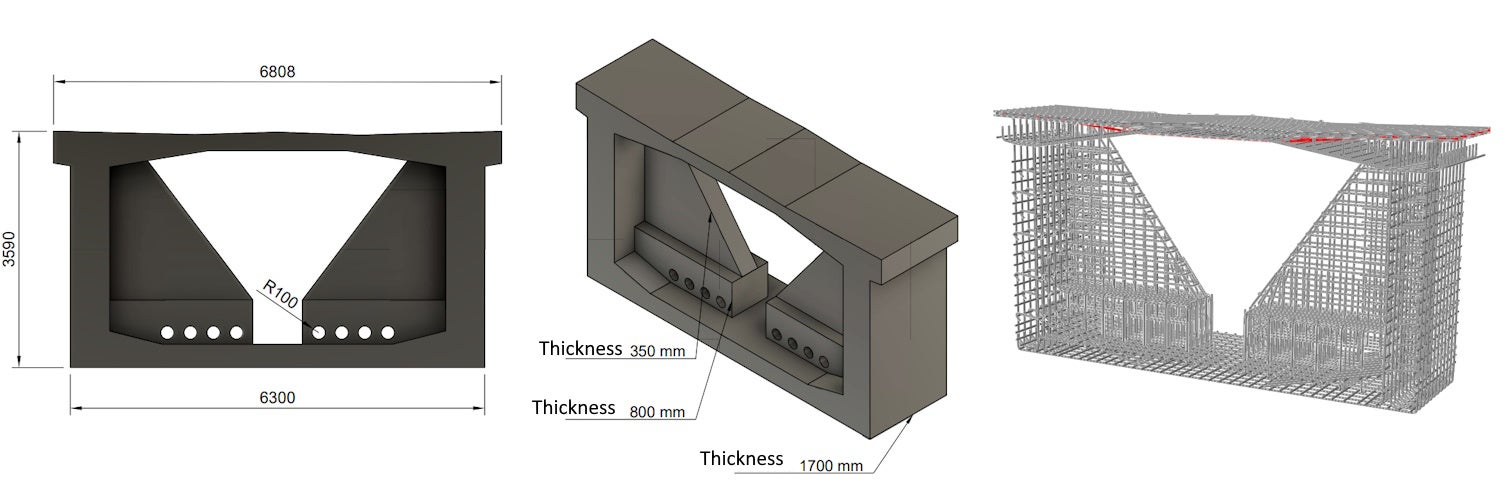
Geometrie a vlastnosti materiálu
Pro účely simulace byl použit výsek modelu části mostní konstrukce, který byl z betonu pevnosti C50/60. Model byl v části horní desky příčně předepnut monostrandy Y1860 S7-15.2 s kotevním napětím 1100 MPa. Betonářská výztuž a její vlastnosti odpovídají výztuži B500B.
Obr. 1 Geometrie a vyztužení
Modely
Pro účely simulace byly vytvořeny tři modely s rozdílnou úrovní komplexnosti. První model (dále Model A) byl řešen jako 2D rovinná úloha se zjednodušením v podobě rovinné napjatosti. Pro řešení byla použita metoda CSFM (Compatible Stress Field Method) [1], která uvažuje návrhové předpoklady výpočtu, které jsou v souladu s platnými normami EN 1992-1-1 [3]. V další fázi byla provedena simulace na druhém modelu (dále Model B), který je řešen prostorově pomocí objemových elementů, zohledňující i třetí směr, tedy podélný směr výseku komorového mostu. Pro Model B se vychází z předpokladu, že počáteční napjatost v podélném směru výseku konstrukce je nulová, a tedy splňuje předpoklady z Modelu A, kde se vychází z modelu rovinné napjatosti. Řešení 3D modelu je postaveno na konstitutivním modelu Drucker – Prager „Concrete Damage Plasticity“ [2]. Veškeré vstupy jsou v souladu se spolehlivostním přístupem založeným na součinitelích spolehlivosti uvedeným v normách [3]. Třetí model (dále Model C) se liší od Modelu B počátečním konstantním podélným tlakovým napětím v průřezu komorového průřezu v podélném směru výseku komory. Počáteční stav se tedy liší od Modelu A.
CSFM – MODEL A
Předpoklady řešení
Model je tvořen 2D konečnými prvky betonu a 1D prvky výztuže. Je uvažováno, že beton přenáší pouze tlakové napětí, tahy jsou přenášeny výztuží. Pevnost betonu v tahu se zanedbává, ale v modelu je uvažována ve formě tahového ztužení na materiálu výztuže. Vzhledem k příčným tahům je uvažováno s tlakovým změkčením betonu na základě fib MC 2010. Soudržnost betonu, betonářské a předpínací výztuže je zahrnuta v podobě elementů soudržnosti, které reprezentuje tuho-plastický diagram s dlouhou plastickou větví. Více se lze dočíst v dokumentu Theoretical background for IDEA StatiCa Detail [1].
Okrajové podmínky a zatížení
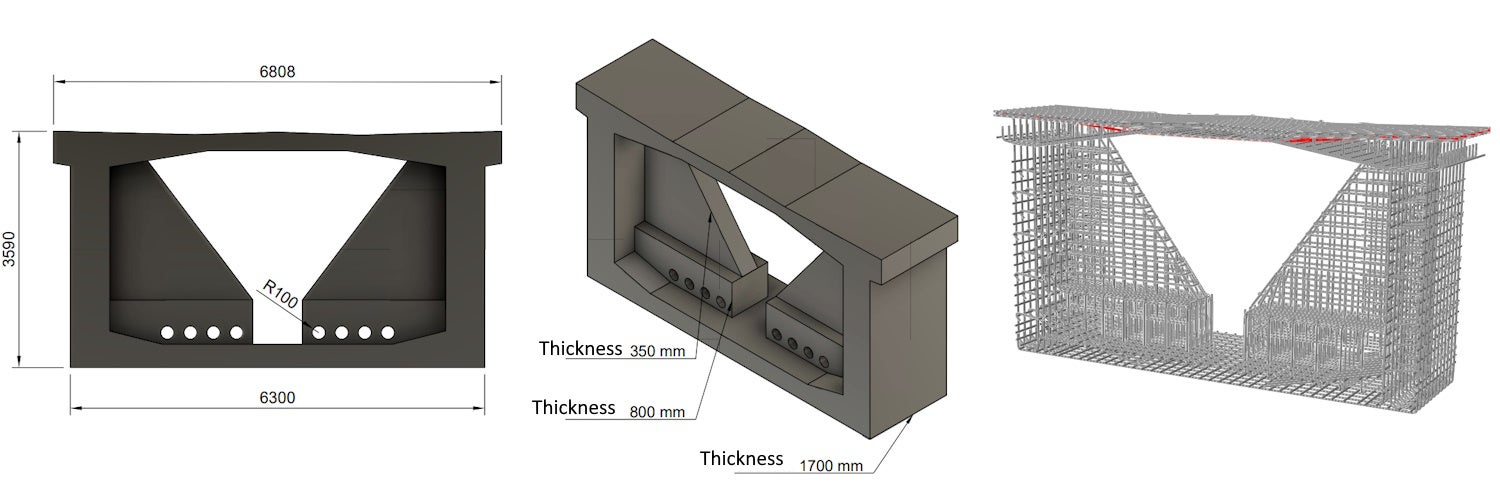
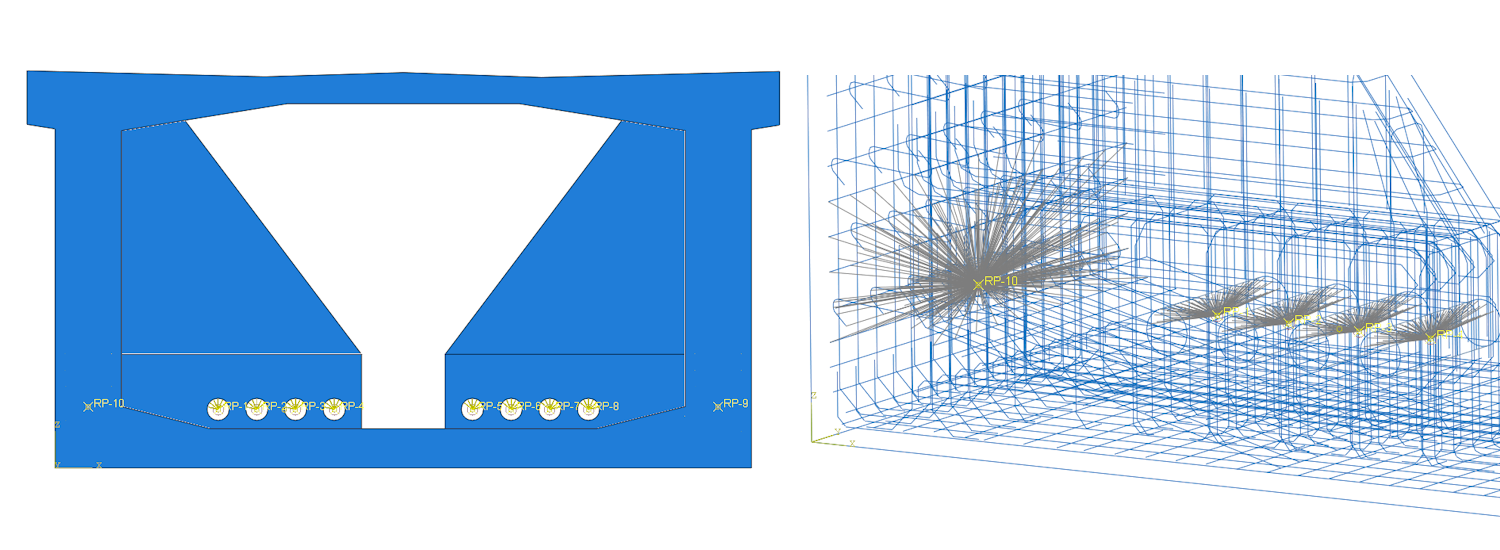
Deviátor se nachází ve třetině rozpětí pole mostní konstrukce. Pro simulaci se umístily podpory ve spodní části stěny komorového průřezu. Podpory byly svázány v poloměru 300 mm s betonářskou výztuží pomocí vazebních rovnic distribučního couplingu. Okrajové podmínky odebíraly dva translační stupně volnosti (svislý a vodorovný posuv) na jedné podpoře a jeden translační stupeň volnosti (svislý posuv) na druhé podpoře. Pro simulaci odezvy deviátoru okrajové podmínky neovlivňují stavy napjatosti a predikují místo porušení deviátoru.
Externí kabely jsou 31 lanné, kotevní napětí kabelu v konstrukci je 1394 MPa, čemuž odpovídají návrhové radiální síly v deviátoru 674 kN ve vertikálním směru a 67 kN v horizontálním směru (cca 10 % vertikální síly, vliv prostorového trasování kabelu). Velikost svislé radiální síly od jednoho kabelu na mezi únosnosti deviátoru byla pomocí Modelu A stanovena na 1980 kN. Pro toto mezní zatížení pak byla provedena analýza mezní únosnosti pomocí jednotlivých modelů. Model uvažuje rovnoměrný roznos radiálního zatížení v podélném směru.
Obr. 2 Okrajové podmínky a maximální zatížení
Výsledky pro model A
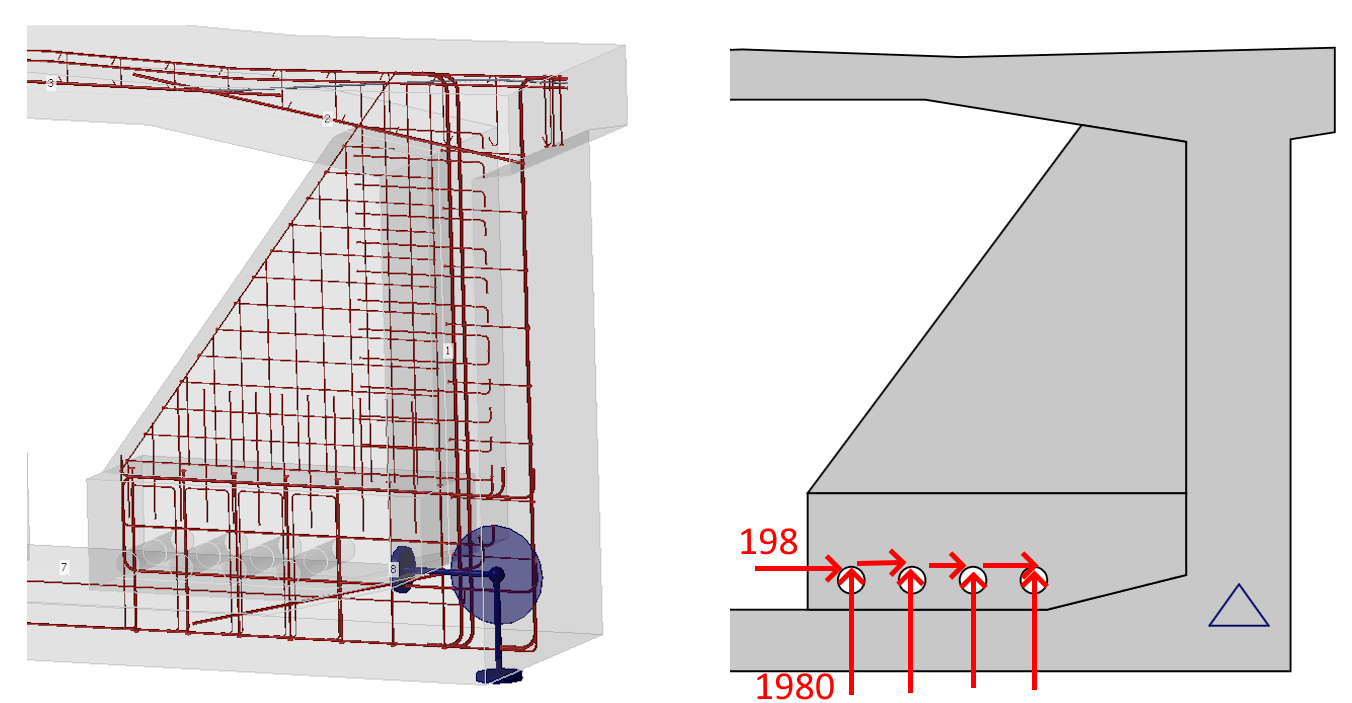
Simulace predikuje místo největšího tlakového namáhání v místě kontaktu kabelu s betonovým deviátorem. Dané místo je obecně oblast koncentrace napětí, kde je beton plně na plasticitě s napětím -28 MPa (což je návrhová pevnost betonu s uvážením faktoru Éta zohledňující křehký lom materiálu). Místo maximálního napětí na výztuži 469 MPa je v oblasti spojení deviátoru a desky komorového průřezu. Toto místo je také kritické z pohledu pevnosti a kotevní délky výztuže, která je také maximálně využita. Na druhou stranu sekundárním místem velkého tahového namáhání je stěna komory příčníku a z pohledu betonu je extrémně zatížena ztužující stěna spojující deviátor se stěnou komorového příčníku.
Obr. 3 Hlavní tlakové napětí v betonu (vlevo), napětí na výztuži (vpravo), maximální napětí na betonu a výztuži
Concrete Damage Model – Model B, C
Předpoklady metody
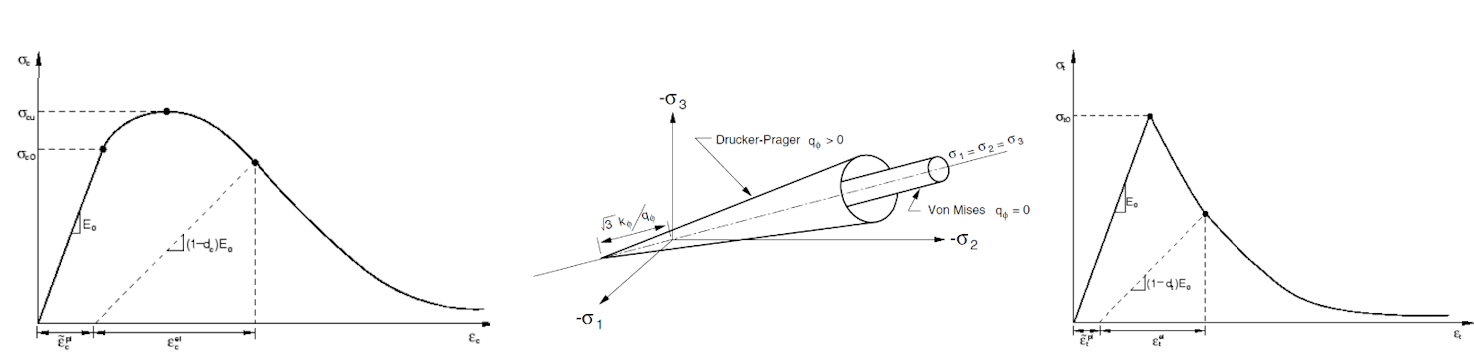
Concrete Damage Plasticity (dále jen CDP) je založen na Drucker – Prager podmínce plasticity [2]. Tento model je vhodný pro materiály s vnitřním třením, jako jsou zeminy nebo beton. Pevnost v tahu je menší než pevnost v tlaku a hydrostatická část tenzoru napjatosti hraje roli při evoluci plochy plasticity. Při obecném namáhání má podmínka plasticity plochu rotačního kužele. Materiálový model pro tlakové a tahové namáhání uvažuje i post-kritické chování, které je řízeno tzv. damage parametry, nabývající hodnot nula až jedna (pro téměř nulovou elastickou tuhost betonu v tlaku nebo v tahu v post-kritickém stavu). Čím je číslo damage parametru větší, tím je element více porušen a nepodílí se na příspěvku tuhosti [2].
Materiálový model
Tvar uniaxiální křivky materiálového modelu v tlaku i v tahu pro beton vychází z Thorenfeldtovy teorie [4]. Veškeré vstupy jsou návrhové hodnoty vycházející ze spolehlivostního přístupu normy EN 1992-1-1 [3]. Materiálový model betonářské výztuže B500B je uvažován s tahovým zpevněním v plastické větvi, stejně tak materiálový model předpínací výztuže Y1860 S7-15.2.
MKP elementy a propojení betonu s výztuží
Pro MKP model betonu byl použit prvek C3D8 neboli hexa-element s lineární bázovou funkcí a 8 integračními body. Betonářská a předpínací výztuž je tvořena T3D2 elementy, které přenáší pouze osové účinky. Interakce výztuže a betonu je zajištěna pomocí MPC vazeb, na nichž je zohledněno tahového ztužení (tension-stiffening), což pokrývá v určité míře model soudržnosti nebo hmoždinkový efekt. Podpory jsou spojeny s výztuží pomocí distribučního couplingu [2].
Obr. 4 Materiálový model v tlaku (vlevo), Drucker-Prager plocha plasticity (střed), materiálový model v tahu (vpravo)
Okrajové podmínky a zatížení
Okrajové podmínky pro Modely B a C jsou identické. Model je zatížen silově a bodová síla je roznesena na plochu kontaktu kabelu s deviátorem pomocí distribučního couplingu, který zaručuje rovnoměrné rozdělení zatížení skrze tloušťku deviátoru. Bodové podpory byly svázány v poloměru 300 mm a skrze tloušťku 1700 mm výseku komorového průřezu s betonářskou výztuží pomocí vazebních rovnic distribučního couplingu
Obr. 5 Model (vlevo), Okrajové podmínky a vazební rovnice pro zatížení a podporu (vpravo)
Výsledky pro model B
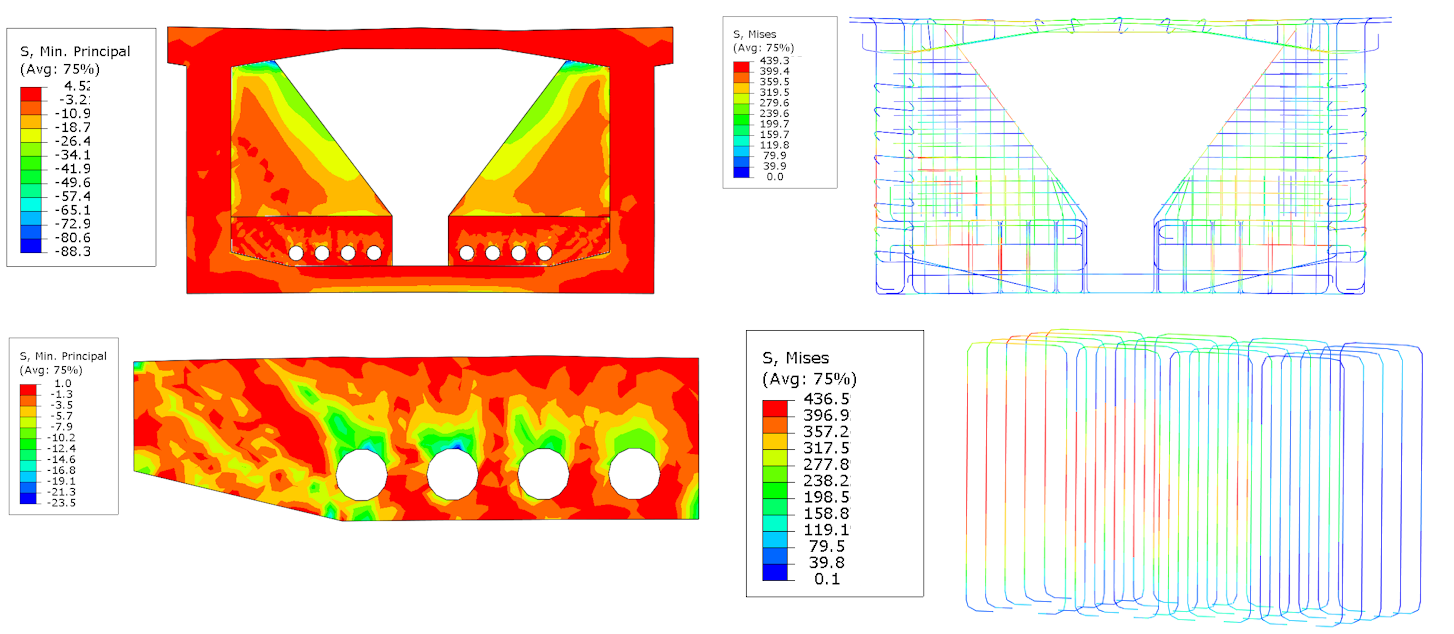
Model B vychází z předpokladu nulové počáteční napjatosti v podélném směru mostu (konzervativní varianta). Díky prostorové napjatosti a převážně díky koncentraci při otlačení rohu se objevuje největší tlakové napětí -88 MPa v oblasti napojení ztužující stěny do horní desky výseku komory. Pokud se zaměříme na oblast deviátoru, dosahujeme maximálního tlakového napětí -23.5 MPa v oblasti kontaktu kabelu s kanálkem. Extrémní napětí betonářské výztuži 439 MPa se objevuje v místě lemující výztuže kanálků externího kabelu a spojení deviátoru s deskou komorového průřezu. Místo extrémního napětí se shoduje s Modelem A.
Obr. 6 Hlavní tlakové napětí v betonu (vlevo), Von-Misses napětí na výztuži (vpravo)
Výsledky pro model C
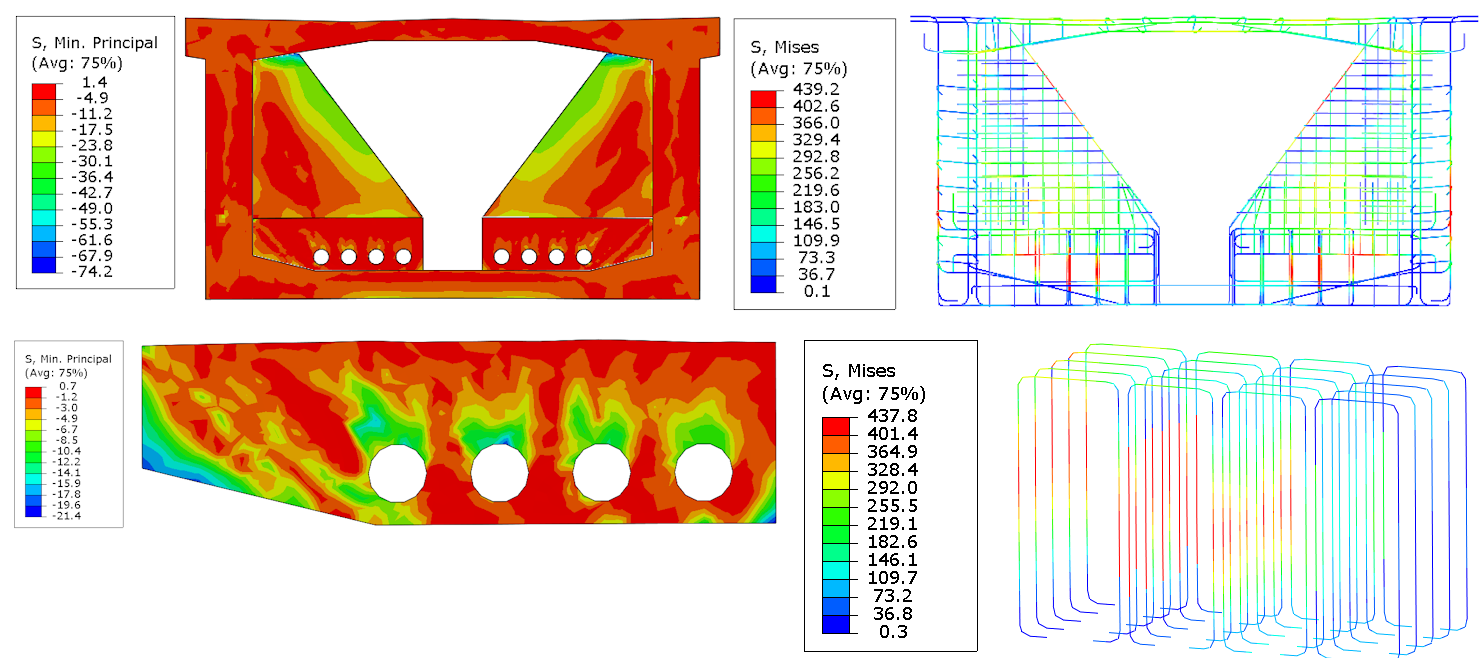
Model C má jako počáteční stav napjatosti tlakové napětí po průřezu komorového výseku. Vzhledem k počátečnímu stavu došlo k přerozdělení napjatosti a hodnota maximálního tlakového napětí poklesla na -74 MPa, avšak místo výskytu zůstalo totožné. Pokud se zaměříme na oblast deviátoru, došlo k mírnému poklesu napjatosti na hodnotu -21.5 MPa. Porovnání modelu B a C ukazuje, že podélná normálová napětí v komorovém průřezu nemají podstatný vliv na vypočtenou únosnost deviátoru, protože o únosnosti prvku rozhodují části konstrukce mimo komorový průřez. Místo a napětí na betonářské výztuži 437 MPa se nezměnilo oproti Modelu B.
Obr. 7 Hlavní tlakové napětí v betonu (vlevo), Von-Misses napětí na výztuži (vpravo)
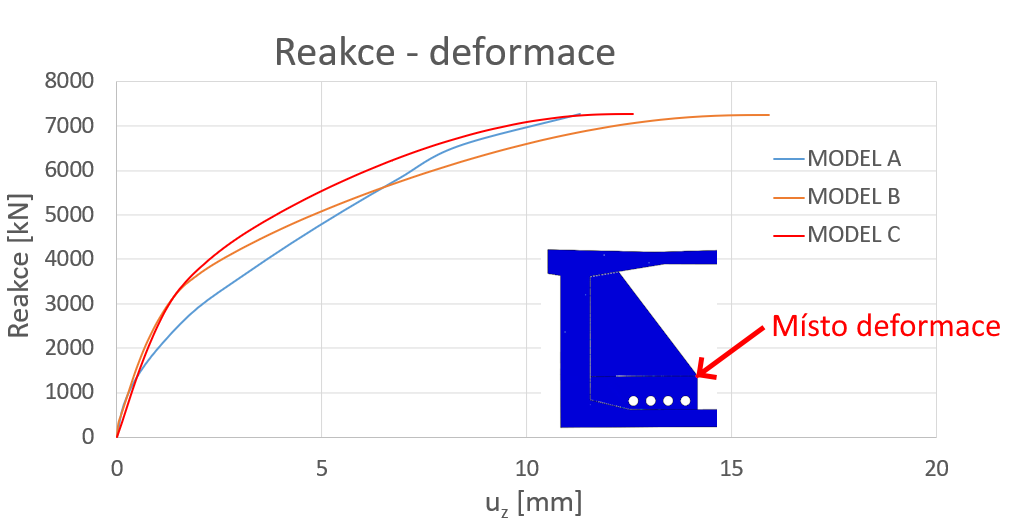
Křivka závislosti deformace na reakci
Komplexní chování modelu je prokázáno křivkou závislosti reakce v podpoře na svislém vektoru deformace. V modelu se odečítala deformace v oblasti napojení deviátoru na ztužující stěnu. Toto místo není zatíženo okrajovou podmínkou nebo vazbou a nedochází ke zkreslení. Rozdíly mezi komplexními Modely B a C a zjednodušeným Modelem A jsou způsobeny uvažováním tahové návrhové pevnosti betonu. Model A má počáteční stav, ve kterém není uvažována pevnost betonu v tahu. Tahové ztužení je přeneseno na model výztuže. V modelu B a C, je uvažováno s návrhovou pevnosti 1.6 MPa dle Thorenfeldt [4], což je o 0.3 MPa nižší hodnota než návrhová pevnost betonu v tahu dle EN 1992-1-1 [3].Výsledná reakce vykazuje při splnění podmínek mezního stavu únosnosti stejnou velikost.
Obr. 8 Graf závislosti reakce na svislé deformaci a porovnání modelů
Závěr
Srovnání
Cílem bylo posoudit stav napjatosti a deformace deviátoru se zaměřením na finální únosnost a splnění předpokladů normy [3]. Sekundárním cílem bylo identifikovat nejefektivnější řešení návrhu deviátoru z pohledu inženýrské praxe a časové úspory. Model A splňoval předpoklady rovinné napjatosti v rovině a je vychází z teorie CSFM [1]. Modely B a C uvažovaly prostorové chování výseku komorového mostu a vycházely z modelu „Concrete Damage Plasticity“ Drucker-Prager [2]. Kritické místo z pohledu hlavních tlakových napětí se lišilo mezi Modely A a Modely B, C. Model A detekoval extrémní tlakové napětí -28 MPa v oblasti kontaktu kabelu s kanálkem deviátoru, zatímco Modely B, C označily místo s extrémním napětím na napojení ztužující stěny s horní deskou komorového průřezu. Hodnota napětí se díky koncentraci a ostrému rohu zvýšila pro Model B na -88 MPa a Model C na -74 MPa. Počáteční stav v Modelu C způsobil snížení hlavního tlakového napětí o 14 MPa. Pokud se zaměříme na část deviátoru v Modelu B, C, tak místo kritického napětí odpovídalo Modelu A a hodnota napětí byla -23.5 MPa pro Model B a -21.4 MPa pro Model C. Lze tedy říct, že část deviátoru z pohledu napětí je kvazi–nezávislá na počátečním stavu napjatosti neboli tlaku v komorovém průřezu. Tahová únosnost betonu a roznos napětí v podélném směru deviátoru pomáhá snížit magnitudu velikosti hlavního tlakového napětí. Lze tedy konstatovat, že deviátor je úloha vhodná pro řešení zjednodušenými modely jako je Model A, neboli metoda CSFM. Kritické místo z pohledu betonářské výztuže je shodné pro všechny modely, a to v místě kabelového kanálku deviátoru ve třmíncích spojujících spodní desku komorového průřezu a deviátoru. Maximální hodnota napětí na Modelu A vykazuje napětí 469 MPa, zatímco model B a C vykazují napětí 439 MPa, což ukazuje na vliv tahové pevnosti betonu. Z pohledu kritického místa je možné usoudit, že i napjatosti v betonářské výztuži vykazují prokazatelnou shodu.
Efektivita řešení
Z pohledu časové úspory a praktických návrhů deviátorů mostních konstrukcí vychází nejlepším řešením Model A, kde se stavební inženýr od přípravy modelu až k vyhodnocení výsledků dostane v řádech hodin, a nikoliv dní, jak tomu bylo u Modelů B, C.
Literatura
[2] Abaqus analysis user's manual. Abaqus analysis user's manual [online] dostupný na www: https://classes.engineering.wustl.edu/2009/spring/mase5513/abaqus/docs/v6.6/books/usb/default.htm?startat=pt05ch18s05abm36.html
[3] ČSN EN 1992-1-1 ed.2 (731201). Eurokód 2: Navrhování betonových konstrukcí – Část 1-1: Obecná pravidla a pravidla pro pozemní stavby. Praha: Český normalizační institut, 2019, 208 s.
[5] ČSN EN 1992-2 (736208). Eurokód 2: Navrhování betonových konstrukcí – Část 2: Betonové mosty – Navrhování a konstrukční zásady. Praha: Český normalizační institut, 2019, 90 s.