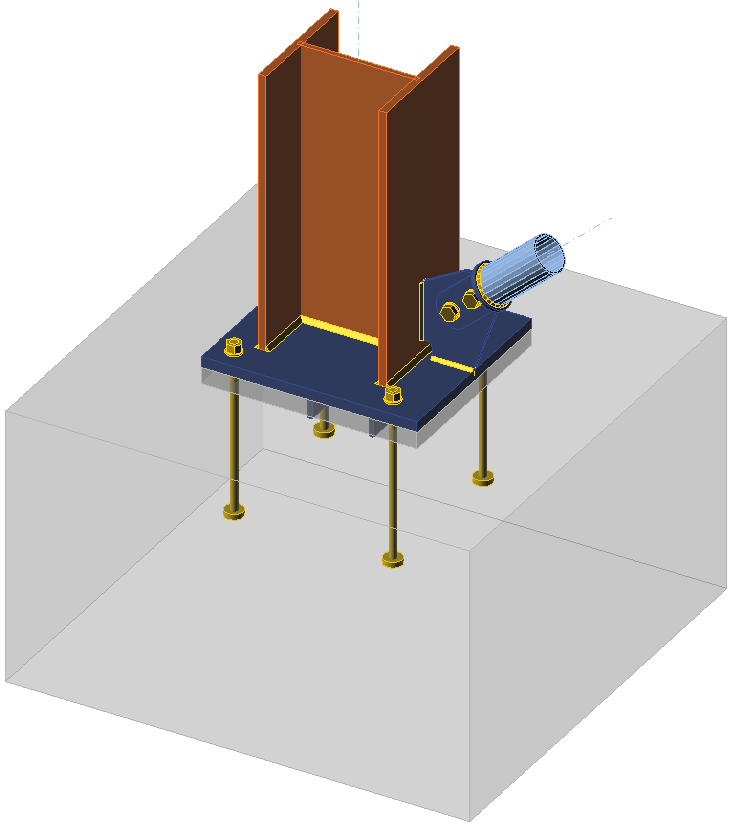
A column with cross-section W12\(\times\)79 is anchored into a concrete block (concrete compressive strength 4 ksi) by four anchor bolts 3/4'' A307 (fy = 50 ksi, fu= 65 ksi). Column base is grouted. A brace is HSS 3.5\(\times\)0.203 connected by gusset plate and 2 slip-critical bolts 3/4'' A490 (fy = 130 ksi, fu = 150 ksi). All steel is grade A36 (fy = 36 ksi, fu = 58 ksi). The shear is transferred via shear lug with cross-section W6\(\times\)25. Weld electrodes E70XX are selected. The column is loaded by compressive force –160 kip, bending moment 1000 kip-in, and shear force 20 kip. The brace is loaded by tensile force 30 kip.
Geometry
Investigated joint
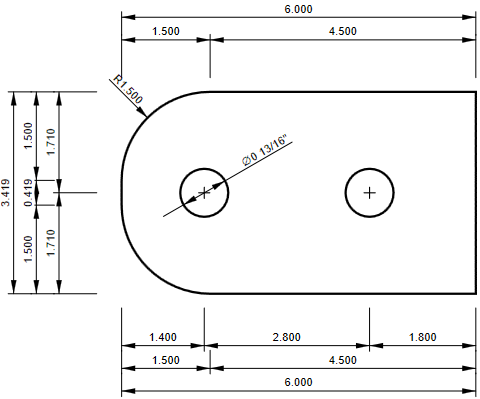
Cross-sections of column (left), brace (middle), and shear lug (right)
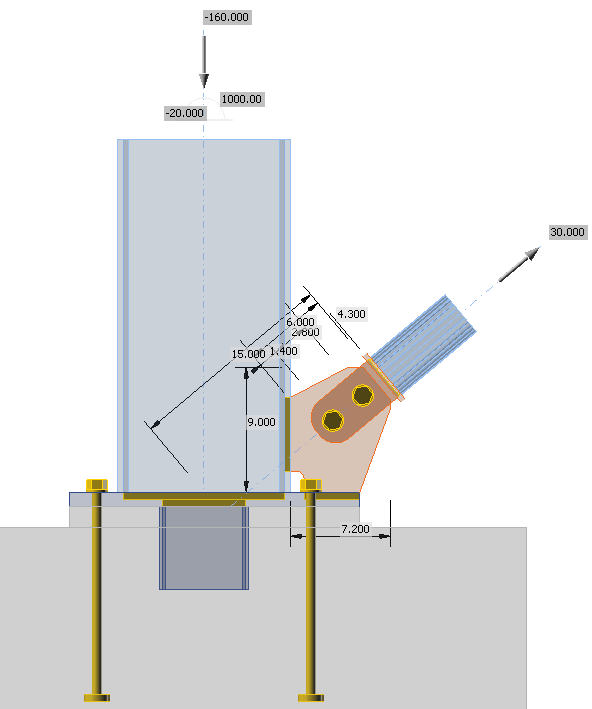
Concrete block dimensions
Gusset plate dimensions and loads on a transparent mode
Manual assessment
Manual check of bolts, welds, plates, and concrete in compression is done according to AISC 360-16. The capacity of shear lug is determined according to ACI 349-01. Anchor rods are designed according to AISC 360-16 – J9 and ACI 318-14 – Chapter 17.
The following checks are required:
- Slip resistance of bolts in shear – AISC 360-16 – J3.8
- Block shear strength – AISC 360-16 – J4.3
- Tensile strength of connected elements – AISC 360-16 – J4.1
- Weld strength – AISC 360-16 – AISC 360-16 – J2.4
- Shear strength of shear lug – AISC 360-16 – G2
- Bending strength of shear lug – AISC 360-16 – F2.1
- Bearing capacity of shear lug against concrete – ACI 349-01 – B.4.5 and RB11
- Concrete breakout strength of the shear lug – ACI 349 – B11
- Concrete bearing strength in compression – AISC 360-16 – J8
- Steel strength of anchors in tension – ACI 318-14 – 17.4.1
- Concrete breakout strength – ACI 318-14 – 17.4.2
- Concrete pullout strength – ACI 318-14 – 17.4.3
- Concrete side-face blowout strength – ACI 318-14 – 17.4.4
The design of beam and column is assumed to be checked elsewhere.
Distribution of forces
The whole shear force is expected to be transferred via the shear lug into the concrete block. The shear is transferred only in the concrete block and the grout is ineffective. The shear force is the sum of shear force in column and the horizontal component of the tensile force in the brace, i.e. \(V=20+30\cdot \cos(40^\circ) = 43\) kip.
The tensile force in the brace, 30 kip, is required to be transferred via two preloaded bolts. The gusset plates and welds needs to be sufficient.
The compressive force, 160 kip, is decreased by the vertical component of the tensile force in the brace. The column base needs to resist compressive force of \(160-30\cdot \sin(40^\circ) = 141\) kip and bending moment 1000 kip-in.
Brace connection check
Slip-critical connection
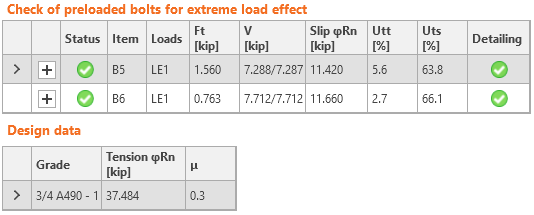
The strength of slip-critical connection is determined according to AISC 360-16 – J3.8. The minimum bolt pretension is taken from Table J3.1 as \(T_b = 35\) kip. The single bolt slip resistance is:
\[\phi R_n = \phi \mu D_u h_f T_b n_s = 1 \cdot 0.3 \cdot 1.13 \cdot 1.0 \cdot 35 \cdot 2 = 24 \textrm{kip}\]
The slip resistance of 2 bolts, 47 kip, is sufficient to transfer the tensile force 30 kip.
Tensile strength of the tongue
The tongue are two plates with the thickness of 1/4'' to avoid eccentricity in compressive loading. The gross and net areas in tension are \(3.4 \cdot (2\cdot 1/4)=1.7\) in2 and \((3.4-13/16)\cdot (2\cdot 1/4)=1.3\) in2, respectively.
\[\phi R_n =\phi F_y A_g = 0.9 \cdot 36 \cdot 1.7 = 55 \textrm{kip} \]
\[\phi R_n =\phi F_u A_n = 0.75 \cdot 58 \cdot 1.3 = 57 \textrm{kip} \]
The strength of the tongue, 55 kip, is sufficient to transfer tensile force, 30 kip. The welds are designed as CJP butt welds and their strength should be the same as the base material.
Tongue dimensions
Gusset plate block shear strength
The expected yield line at gusset plate for block shear failure is 6.6 in long, the rupture may occur at line shorter by the bolt hole, i.e. 5.8 in. The gusset plate thickness is 3/8''.
\[\phi R_n =\phi F_y A_g = 0.9 \cdot 36 \cdot 2.5 = 80 \textrm{kip} \]
\[\phi R_n =\phi F_u A_n = 0.75 \cdot 58 \cdot 2.2 = 94 \textrm{kip}\]
The strength of the gusset, 80 kip, is sufficient to transfer tensile force, 30 kip.
Gusset plate weld strength
The fillet welds are designed on both sides of the gusset plate with the size 1/4''. The lengths of the welds are 5.2 in and 4.0 in. To avoid calculating the eccentricity, it is conservatively assumed that both welds are 4 in long and both welds transfer half of the load. The critical weld is the one loaded at an angle 40\(^\circ\).
\[F_{nw} = 0.6 F_{EXX} (1+0.5 \sin^{1.5} \theta) = 0.6 \cdot 70 \cdot (1+0.5 \sin^{1.5} 40^\circ) = 53 \textrm{ksi} \]
\[\phi R_n = \phi F_{nw} A_{we} = 0.75 \cdot 53 \cdot 2.83 = 112 \textrm{kip}\]
The strength of the welds at the gusset, 224 kip, is sufficient to transfer tensile force, 30 kip.
Column base check
The column base needs to resist compressive force of \(P_u=160-30\cdot \sin(40^\circ) = 141\) kip and bending moment \(M_u=1000\) kip-in. Since the supporting area, A2, is sufficiently large, the concrete bearing strength is
\[\phi f_{p,(\max)}= \phi 1.7 f'_c = 0.65 \cdot 1.7 \cdot 4 = 4.4 \textrm{ksi} \]
\[\phi q_{\max} = f_{p,(\max)} B = 4.4 \cdot 19 = 83.6 \textrm{kip/in}\]
The base plate is elongated due to the gusset connection of the brace. It is conservatively assumed that the compressive force is acting at the column flange, i.e. e = 6.18 in from the connection center. The distance between anchor bolt and connection center is f = 7.68 in.
\[M_u= eP_r+2fN_{ua} \]
\[N_{ua}=\frac{M_u-eP_r}{2f}=\frac{1000-6.18 \cdot 141}{2\cdot 7.68}=8.4 \textrm{kip} \]
\[Y = \frac{P_r+2N_{ua}}{q_{\max}} = \frac{141+2\cdot 8.4}{83.6} = 1.9 \textrm{in}\]
The bearing resistance of the concrete is sufficient, because the base plate is large enough to accommodate bearing area length, Y, and the tensile force in anchor is 8.4 kip. More detailed base plate check with the check of base plate yielding should be provided for the load case with maximum compressive force.
Anchor design
Anchors are 3/4'', grade A307, 12 in embedded length in the concrete block with circular washer plates with diameter 1.8 in. Anchors are loaded only in tension because shear is transferred via shear lug. The check of anchors is provided according to ACI 318-14 – Chapter 17. Steel strength and pullout strength is provided for individual anchors and concrete breakout strength and concrete side-face blowout strength is provided for group of anchors because \(3h_{ef} \ge s\), where \(h_{ef}\) is the embedment depth and s is anchor spacing.
Steel strength of an anchor in tension – 17.4.1
\[\phi N_{sa}=\phi A_{se,N} f_{uta} \]
\[\phi N_{sa}= 0.7 \cdot 0.334 \cdot 60 = 14 \textrm{kip}\]
Concrete breakout strength – 17.4.2
\[h_{ef}=\min \left( \frac{c_{a,\max}}{1.5}, \frac{s}{3} \right ) \le h_{ef} = \max \left(\frac{14}{1.5}, \frac{15.1}{3} \right ) = 9.33 \le 12 \textrm{in} \]
\[A_{Nc} = (14+1.8/2+14) \cdot (14+15.1+14)=1245 \textrm{in}^2 \]
\[A_{Nco} = 9 h_{ef}^2 = 9 \cdot 9.33^2 = 783 \textrm{in}^2 \]
\[N_b = k_c \lambda_a \sqrt{f'_c} h_{ef}^{1.5} = 24 \cdot 1 \cdot \sqrt{4000} \cdot 9.33^{1.5} = 43.3 \textrm{kip} \]
\[\psi_{ec,N} = \frac{1}{1+\frac{2 e'_N}{3 h_{ef}}} = \frac{1}{1+\frac{2 \cdot 0}{3 \cdot 9.33}} = 1 \]
\[\psi_{ed,N} = \min \left ( 0.7 + \frac{0.3 c_{a,min}}{1.5 h_{ef}}, 1 \right ) = \min \left ( 0.7 + \frac{0.3 \cdot 14}{1.5 \cdot 9.33}, 1 \right ) = 1 \]
\[\phi N_{cbg} = \phi \frac{A_{Nc}}{A_{Nco}} \psi_{ec,N} \psi_{ed,N} \psi_{c,N} \psi_{cp,N} N_b \]
\[\phi N_{cbg} = 0.7 \cdot \frac{1245}{783} \cdot 1 \cdot 1 \cdot 1 \cdot 1 \cdot 43.3 = 48 \textrm{kip}\]
Concrete pullout strength – 17.4.3
\[A_{brg} = \pi \left ( \frac{d_{wp}^2-d_a^2}{4} \right ) = \pi \left ( \frac{1.8^2-0.75^2}{4} \right ) = 2.1 \textrm{in}^2 \]
\[N_p = 8 A_{brg} f'_c = 8 \cdot 2.1 \cdot 4 = 67 \textrm{kip} \]
\[\phi N_{pn} = \phi \psi_{c,P} N_p = 0.7 \cdot 1 \cdot 67 = 47 \textrm{kip}\]
Concrete side-face blowout strength – 17.4.4
\[red = \frac{1+\frac{c_{a2}}{c_{a1}}}{4} = \frac{1+\frac{14}{14}}{4} = 0.5 \]
\[\phi N_{sb} = \phi 160 c_{a1} \sqrt{A_{brg}} \sqrt{f'_c} = 0.7 \cdot 160 \cdot 14 \cdot \sqrt{2.1} \cdot \sqrt{4000}= 144 \textrm{kip} \]
\[\phi N_{sbg} = n \cdot red \cdot \phi N_{sb} = 2 \cdot 0.5 \cdot 144 = 144 \textrm{kip}\]
The smallest resistance is that of the anchor steel, 14 kip. It is sufficient to transfer the load 8.4 kip.
Shear lug design
The whole shear force is expected to be transferred via the shear lug into the concrete block. The shear is transferred only in the concrete block and the grout is ineffective. The shear force is the sum of shear force in column and the horizontal component of the tensile force in the brace, i.e. \(V=20+30\cdot \cos(40^\circ) = 43\) kip. The shear lug cross-section is W6x25 and it is 6 in long. The grout layer is 1.5 in thick, so the shear lug is embedded 4.5 in in concrete block. The concrete pressure is assumed as uniform in the concrete block. The bending moment acting on shear lug is equal to shear force acting on lever arm 1.5 + 4.5 / 2 = 3.75 in, i.e. Mu = 161 kip-in. It is expected that fillet welds on shear lug flanges and web are transferring bending moment and shear, respectively. The fillet welds at the flanges need to transfer 161 / 5.9 = 27.3 kip.
Bearing capacity of shear lug against concrete – ACI 349-01 – B4.5 and RB11
\[N_y = n A_{se} F_y = 4 \cdot 0.334 \cdot 36 = 48 \textrm{kip} \]
\[\phi P_{br}=\phi 1.3 f'_c A_1 + \phi K_c (N_y - P_a) \]
\[\phi P_{br}=0.7 \cdot 1.3 \cdot 4 \cdot 27.3 + 0.7 \cdot 1.6 \cdot (48 + 141) = 311 \textrm{kip} \ge 43 \textrm{kip}\]
Concrete breakout strength of the shear lug – ACI 349-01 – B11
\[A_{Vc} = (18.5+6.1+18.5) \cdot (4.5+20) - 6.1 \cdot 4.5 = 1028 \textrm{in}^2 \]
\[\phi V_{cb} = A_{Vc} 4 \phi \sqrt{f'_c} = 1028 \cdot 4 \cdot 0.85 \cdot \sqrt{4000} = 221 \textrm{kip} \ge 43 \textrm{kip}\]
Shear strength of shear lug – AISC 360-16 – G2
\[\phi V_n = 0.6 F_y A_w C_{v1}= 1 \cdot 0.6 \cdot 36 \cdot 2 \cdot 1 = 44 \textrm{kip} \ge 43 \textrm{kip}\]
Fillet welds of shear lug web – AISC 360-16 – J2.4
\[F_{nw} = 0.6 F_{EXX} (1+0.5 \sin^{1.5} \theta) = 0.6 \cdot 70 \cdot (1+0.5 \sin^{1.5} 0^\circ) = 42 \textrm{ksi} \]
\[\phi R_n = \phi F_{nw} A_{we} = 0.75 \cdot 42 \cdot 1.93 = 61 \textrm{kip} \ge 43 \textrm{kip}\]
Bending strength of shear lug – AISC 360-16 – F2.1
\[\phi M_n = \phi M_p = F_y Z_x = 0.9 \cdot 36 \cdot 18.9 = 680.4 \textrm{kip-in} \ge 161 \textrm{kip-in}\]
Fillet welds of the shear lug flange – AISC 360-16 – J2.4
\[F_{nw} = 0.6 F_{EXX} (1+0.5 \sin^{1.5} \theta) = 0.6 \cdot 70 \cdot (1+0.5 \sin^{1.5} 90^\circ) = 63 \textrm{ksi} \]
\[\phi R_n = \phi F_{nw} A_{we} = 0.75 \cdot 63 \cdot 2.1 = 100 \textrm{kip} \ge 27.3 \textrm{kip}\]
The shear and bending strength of the shear lug, weld strength, concrete bearing strength and concrete breakout strength are enough to transfer shear force 43 kip.
Check in IDEA StatiCa
The plates are checked by finite element analysis. The bilinear material model is used with the yield strength multiplied by steel resistance factor \(\phi = 0.9\). The forces acting on other components of the connection, i.e. bolts and welds, are also determined by finite element analysis but their resistance is checked using standard formulas from AISC 360-16, ACI 318-14, and ACI 349-01. The most stressed weld element is checked and with further loading, the stress in weld is spreading into further weld elements. Therefore, the ultimate weld resistance is higher than simply dividing the force by weld utilization.
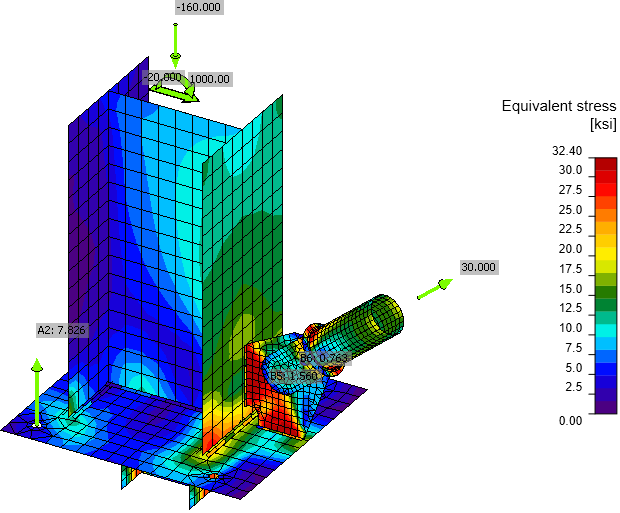
Von Mises stress
Plastic strain including the tensile forces in anchors
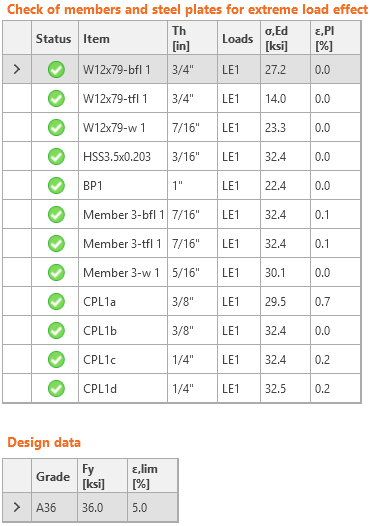
Check of stress and strain of plates
Check of slip-critical connection
Check of welds
Check of anchors
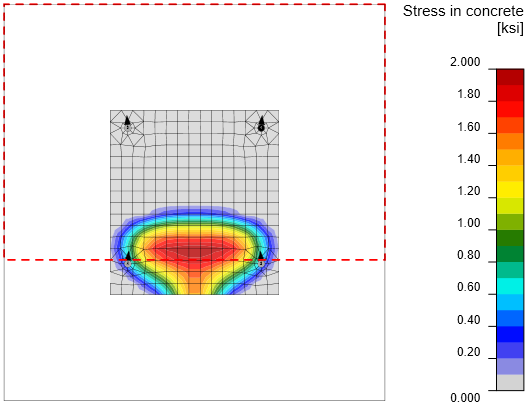
Check of concrete in bearing
Stress in concrete under the base plate and area of concrete cone breakout
Check of shear lug – bearing capacity and concrete breakout strength
Comparison
It is clear that the finite element analysis shows different distribution of internal forces than simple assumptions. The gusset plate also helps transferring the bending moment and thus gusset plate and its welds are much more loaded than in standard design assumptions. The forces in anchors are slightly lower in IDEA because the stress below base plate is not exactly under the column flange. The most heavily utilized element in manual assessment is the web of the shear lug. In IDEA StatiCa, the equivalent stress on the shear lug web is at 30.1 kip which is close to yielding.
The check in design software IDEA StatiCa Connection is in agreement with the manual assessment according to AISC 360, ACI 318, and ACI 341. The small differences are caused mainly by simplifications in hand calculations.
Attached Downloads
- AISC.pdf (PDF, 1.2 MB)