Verification study: Shear connections with coped beams (AISC)
Mark D. Denavit and Rick Mulholland prepared this verification example in a joint project of The University of Tennessee and IDEA StatiCa.
Description
A comparison between results from the component-based finite element method (CBFEM) and traditional calculation methods used in US practice for simple shear connections between a girder and a coped beam is presented in this study. The study focuses on limit states specifically associated with beam copes. Single-coped beams (cope in the top flange only) and double-coped beams (cope in the top and bottom flange) are evaluated.
Traditional calculations were performed in accordance with the provisions for load and resistance factor design (LRFD) in the AISC Specification (2016) with limit states for coped beams as described in Part 9 of the 15th Edition AISC Manual (2017) and Dowswell (2018).
The CBFEM results were obtained from IDEA StatiCa version 22.1. The maximum permitted loads were determined iteratively by adjusting the applied load input to a value that the program deems safe but if increased by a small amount (0.1 kip) the program would deem unsafe by exceeding the 5% plastic strain limit, exceeding 100% bolt or weld utilization, or with a buckling ratio less than 3.0. DR type analyses can help identify maximum permitted loads. However, some approximation is made in the evaluation of the joint design resistance, therefore all results in this report are based on EPS type analysis.
Single Coped Beams
The strength of single-coped beams was evaluated against the following four parameters:
- Cope length
- Web thickness
- Coped corner radius
- Location of the applied force from node
When investigating the cope length and location of the applied force from the node, two different connection types were used: an all-bolted double-angle connection and a bolted/welded shear end plate connection. Only the bolted/welded shear end plate connection was used in the evaluation of web thickness and coped corner radius.
The limit state of flexural local web buckling (as described in Part 9 of the AISC Manual) and limit states pertaining to the specific connection configuration as described in the following sections were evaluated and compared to the results of the CBFEM analysis from IDEA StatiCa.
Effect of Cope Length (All-Bolted Double Angle Connection)
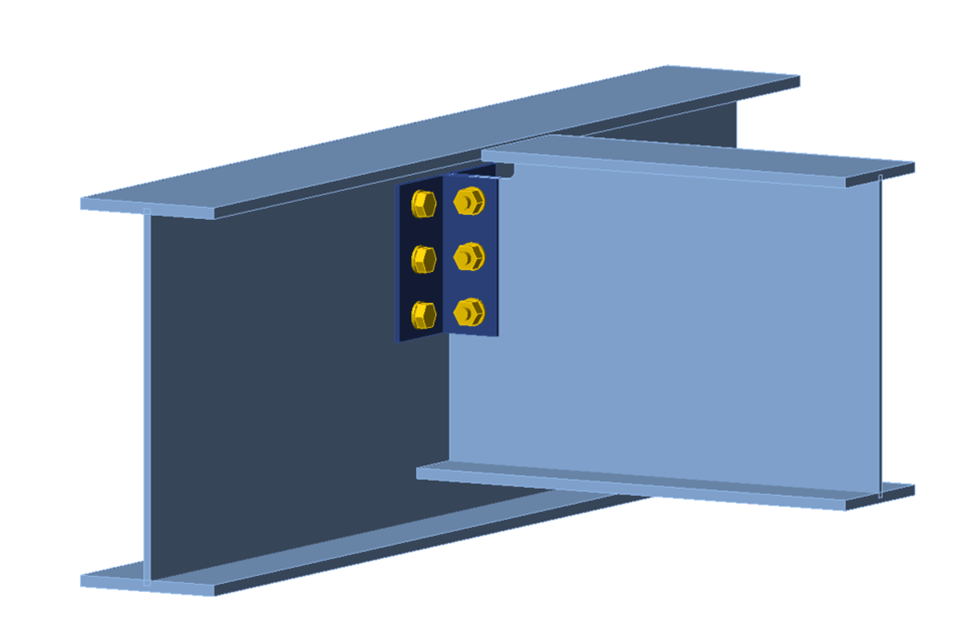
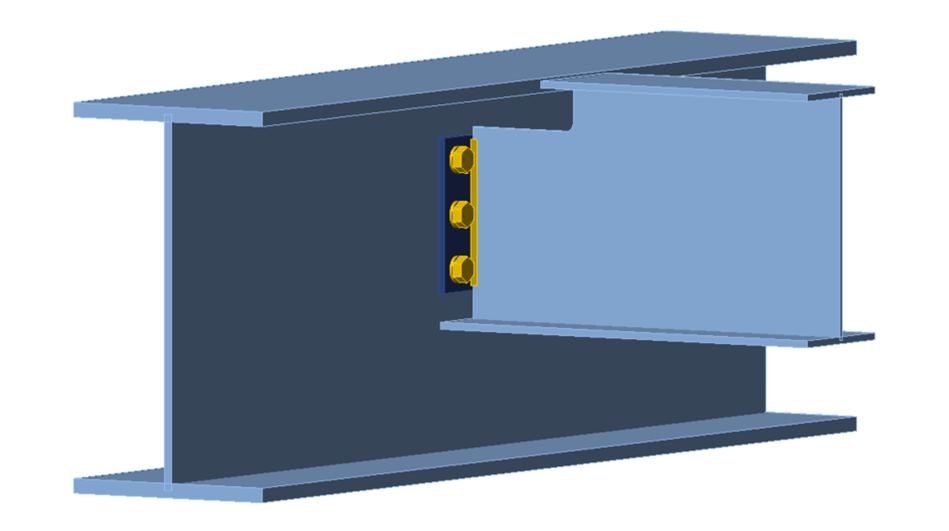
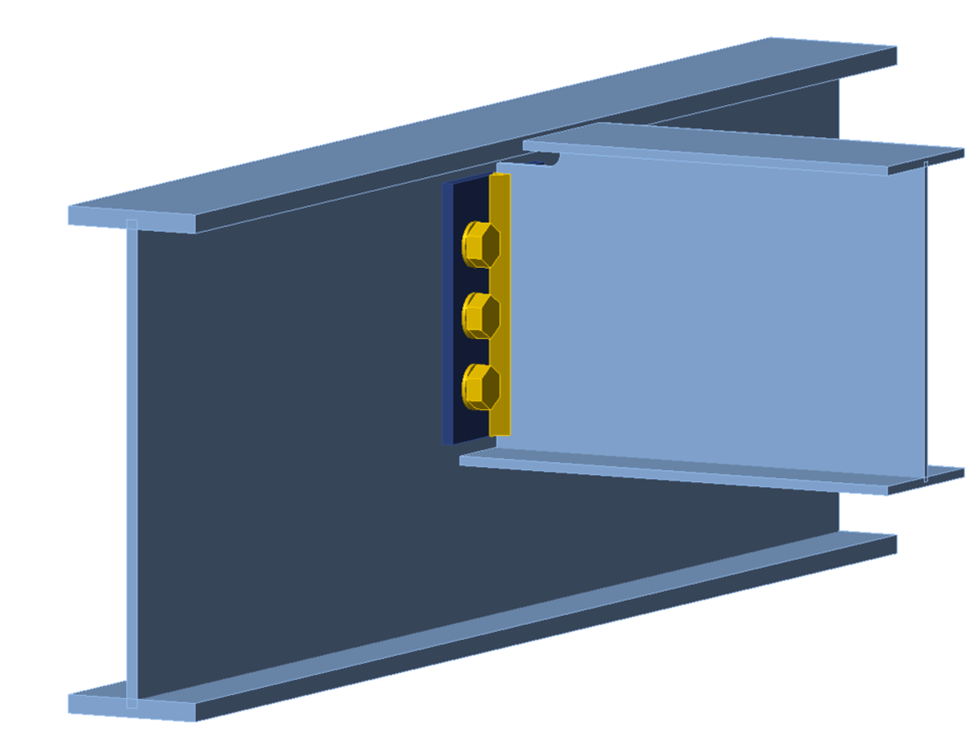
The configuration of this example matches that of Example II.A-4 of the AISC Design Examples v15.1 (AISC, 2019), with the double angle modified to conform to ASTM A529 Gr 55 (Fy = 55 ksi and Fu = 70 ksi). The change in angle material was made to highlight limit states related to the beam cope. The point of force application is set to the face of the girder web and a N-Vy-Vz-Mx-My-Mz model type was used for the beam. A three-dimensional view of the connection is presented in Figure 1.
Figure 1 Three-dimensional view of single coped beam (all bolted double angle connection)
The limit states evaluated for the web of the coped beam are flexural local web buckling, shear yielding, shear rupture, and block shear rupture. Additional limit states for the connection are bolt shear rupture, bearing and tearout for the bolt group between the beam web and angle, shear yielding of the angle, shear rupture of the angle, block shear rupture of the angle, and bolt shear rupture, bearing and tearout for the bolt group between the angle and girder web.
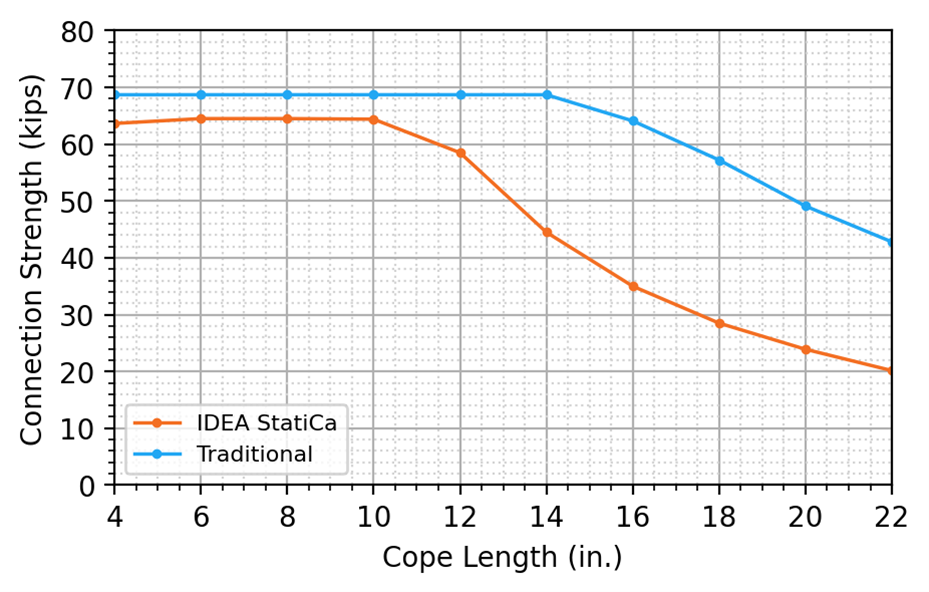
Calculations were performed for 10 cope lengths ranging from 4 to 22 in. in 2-in. increments. The longer cope lengths would rarely, if ever, be practical but are examined here to evaluate the limit state of flexural local web buckling. The maximum factored shear load that can be applied to the connection (i.e., the connection strength) is presented in Figure 2.
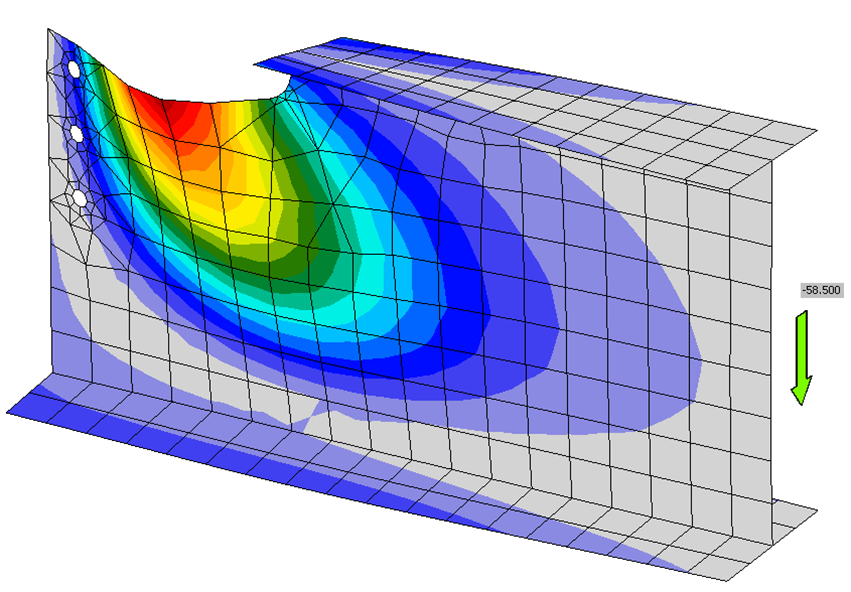
For both the traditional calculations and IDEA StatiCa, the connection strength is relatively constant for lower values of cope length, then decreases with additional cope length. For the traditional calculations, connections with cope lengths of 14 in. or less were governed by block shear rupture of the beam web, and flexural local web buckling of the coped beam web governed connections with cope lengths greater than 14 in. For IDEA StatiCa, connections with cope lengths of 10 in. or less were governed by the 5% plastic strain limit of the beam web, and connections with cope lengths greater than 10 in. were governed by a buckling ratio limit of 3.0. The buckled shape for the connection with a 12 in. cope length is presented in Figure 3; the shape is consistent with flexural local web buckling.
The connection strength is lower for IDEA StatiCa than for the traditional calculations for the entire range of lengths investigated. The difference in strength is greater when buckling controls due to the conservative nature of the buckling ratio limit of 3.0. The limit of 3.0 is recommended for local buckling. Use of this limit is analogous to using only compact members beam design since adhering to the limit allows design without considering local buckling. However, the buckling ratio limit necessary to avoid local buckling depends on the configuration of the element and has not been specifically identified for flexural local web buckling as it has for other types of buckling (e.g., Stability of Bracket Plates using Local Buckling Analysis and Material Nonlinear Analysis and Buckling analysis according to AISC.
Figure 2 Connection strength vs cope length for single coped beam (all-bolted double angle connection)
Figure 3 Buckled shape for single coped beam (all-bolted double angle connection, 12-in. cope length)
Effect of Cope Length (Bolted/Welded Shear End Plate)
The beam used in this example is a W14x30 with a 3-in. cope depth, and the girder is a W21x101 with a modified (i.e., reduced) flange width to accommodate varying cope lengths. Both the beam and girder conform to ASTM A992 (Fy = 50 ksi and Fu = 65 ksi). The end plate is 6 in. wide by 8.5 in. deep, has a thickness of 3/8 in., and conforms to ASTM A36 (Fy = 36 ksi and Fu = 58 ksi). The bolt group consists of a single line of 3 bolts on either side of the beam web. The bolts conform to ASTM F3125 Gr A325 Group A with threads not excluded from shear planes. The beam is welded to the end plate on both sides of the beam web with a 1/4-in. fillet weld (E70XX). The design strengths in Table 10-4 of the AISC Manual for bolted/welded shear end plate connections were calculated assuming the weld length is reduced by one weld size on each end of the weld. The reason for stopping the welds short is to avoid notches in the base metal as described in a user note in AISC Specification Section J2.2b. For a more consistent comparison, the weld length in IDEA StatiCa was manually decreased to 8 in. The point of force application was set to the face of the girder web and a N-Vy-Vz-Mx-My-Mz model type was used for the beam. A three-dimensional view of the connection is presented in Figure 4.
Figure 4 Three-dimensional view of single coped beam (bolted/welded shear end plate connection)
The limit states evaluated for the web of the coped beam are flexural local web buckling, shear yielding, and base metal (web) strength at the weld. Additional limit states for the connection are weld rupture, base metal (plate) strength at the weld, shear yielding of the plate, shear rupture of the plate, block shear rupture of the plate, and shear transfer between the plate and girder.
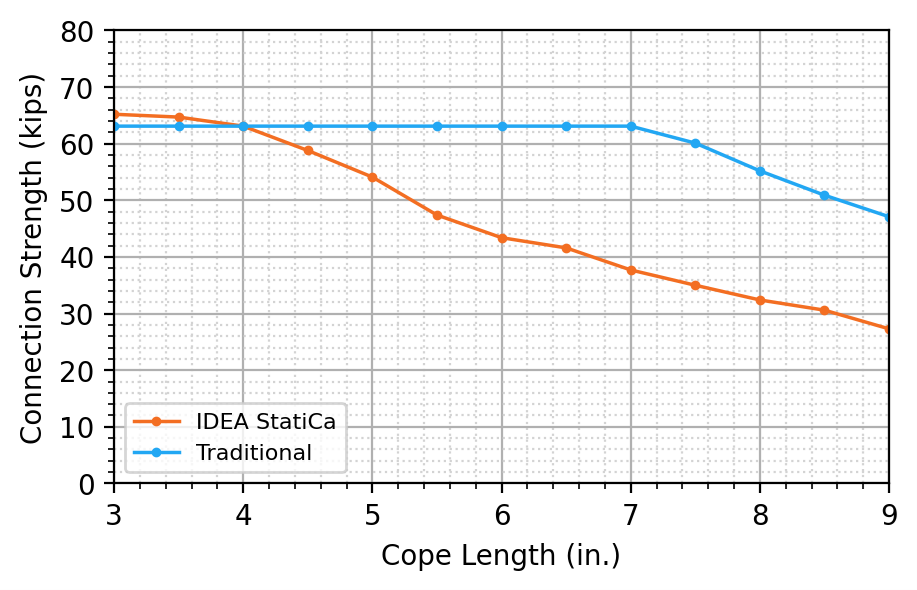
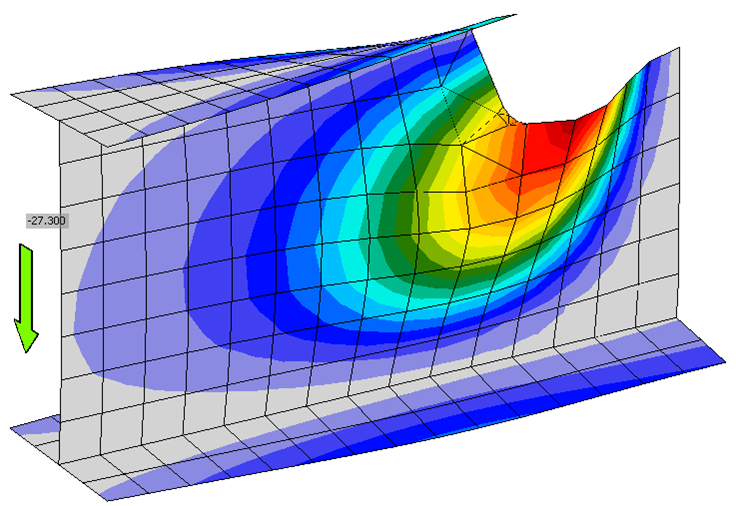
Calculations were performed for 13 cope lengths ranging from 3 to 9 in. in 1/2-in. increments. The maximum factored shear load that can be applied to the connection is presented in Figure 5. For the traditional calculations, the connection strength was constant for connections with up to a 7-in. cope length with the web base metal strength at the weld line controlling. Connections with cope lengths beyond 7 in. were controlled by the limit state of flexural local web buckling. For the IDEA StatiCa analysis, the weld strength controlled the strength of connections with cope lengths of 3 and 3-1/2 in., and the 3.0 buckling ratio limit controlled the strength of connections with cope lengths greater than 3-1/2 in. The buckled shape for the connection with a 9 in. cope length is presented in Figure 6.
The strength from IDEA StatiCa is slightly greater than from the traditional calculations for the connections with cope lengths of 3 and 3-1/2 in. The web base metal strength check controlled the traditional calculations for these connections. IDEA StatiCa captures this limit state with the 5% plastic strain limit, so minor differences are expected. However, for all cases where the limit state of flexural local web buckling controls, the strength from IDEA StatiCa is less than that from the traditional calculations. As observed in the previous section, this is primarily due to the conservative nature of the 3.0 buckling ratio limit.
Figure 5 Connection strength vs cope length for single coped beam (bolted/welded shear end plate connection)
Figure 6 Buckled shape for single coped beam (bolted/welded shear end plate, 9-in. cope length)
Effect of Beam Web Thickness
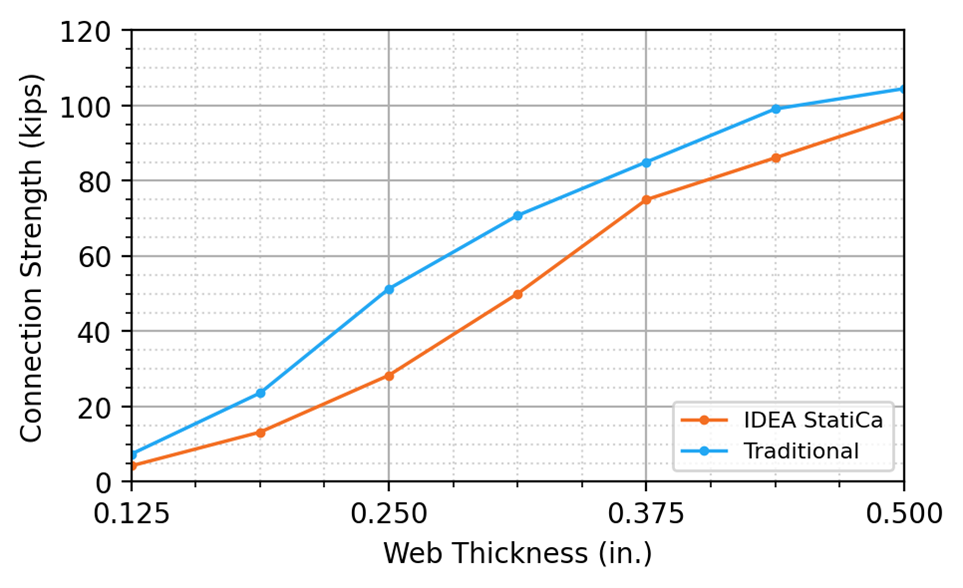
To evaluate the effect of web thickness for a single coped beam, the same bolted/welded shear end plate connection configuration from above was used, with a top cope of length 7-1/2 in. and depth 3in. The W14x30 beam web thickness was modified to values of 1/8 to 1/2 in. in 1/16-in. increments. The nominal web thickness of a W14x30 is 0.270 in. The maximum factored shear load that can be applied to the connection is presented in Figure 7.
As expected, the connection strength increased with increasing web thickness for both the traditional calculations and IDEA StatiCa. For the traditional calculations, the limit state of flexural local web buckling of the coped beam web controlled for connections with web thicknesses of 1/8 in. to 1/4 in. For connections with web thicknesses of 5/16 in. to 7/16 in., the web base metal strength at the weld controlled, and at a web thickness of 1/2 in., the bolt group strength between the plate and girder web controlled. For the IDEA StatiCa analysis, the buckling ratio limit of 3.0 controlled for connections with web thicknesses of 5/16 in. or less, and the 5% plastic strain limit at the reentrant corner of the cope controlled for connections with web thicknesses greater than 5/16 in. The connection strength from IDEA StatiCa was conservative in comparison to the traditional calculations over the entire range investigated.
Figure 7 Connection strength vs web thickness for single coped beam
Effect of Coped Corner Radius
The equations provided in Part 9 of the AISC Manual do not consider the coped corner radius, however Section M2.2 of the AISC Specification states, “Reentrant corners shall be formed with a curved transition. The radius need not exceed that required to fit the connection.” A user note in the same section states, “Reentrant corners with a radius of 1/2 to 3/8 in. (13 to 10 mm) are acceptable for statically loaded work.”
IDEA StatiCa allows for a rounding radius to be applied to notched sections. To investigate the effect of the designated rounding radius on the strength of the coped beam, a bolted/welded shear end plate connection similar to that of the previous two examples was used, with modifications made to the girder and connecting elements in order to ensure that the 5% plastic strain limit at the reentrant corner of the coped beam controlled the strength in IDEA StatiCa. The W21x101 flange was modified to have a width bf = 6 in. to allow for a 3-in. cope length. The end plate was modified to be 8 in. wide and 11 in. deep, with a 1/2-in. thickness. The bolt diameter was increased to 1 in., and the weld size was increased to 5/8 in. A three-dimensional view of the connection is presented in Figure 8.
Figure 8 Three-dimensional view of the shear end plate connection used in analyzing the effect of corner radius
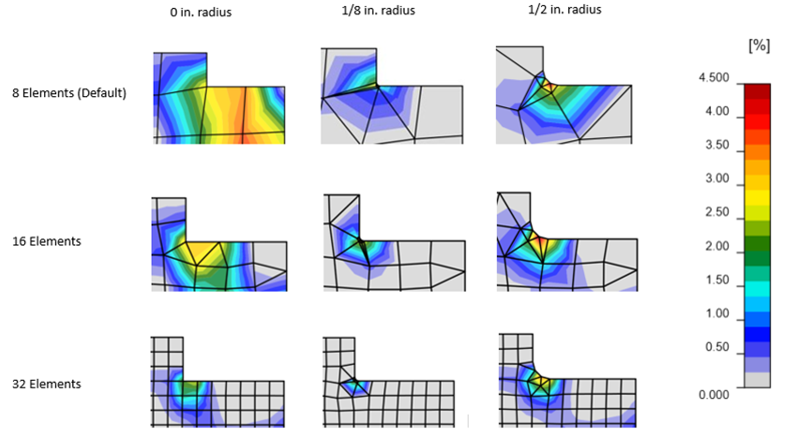
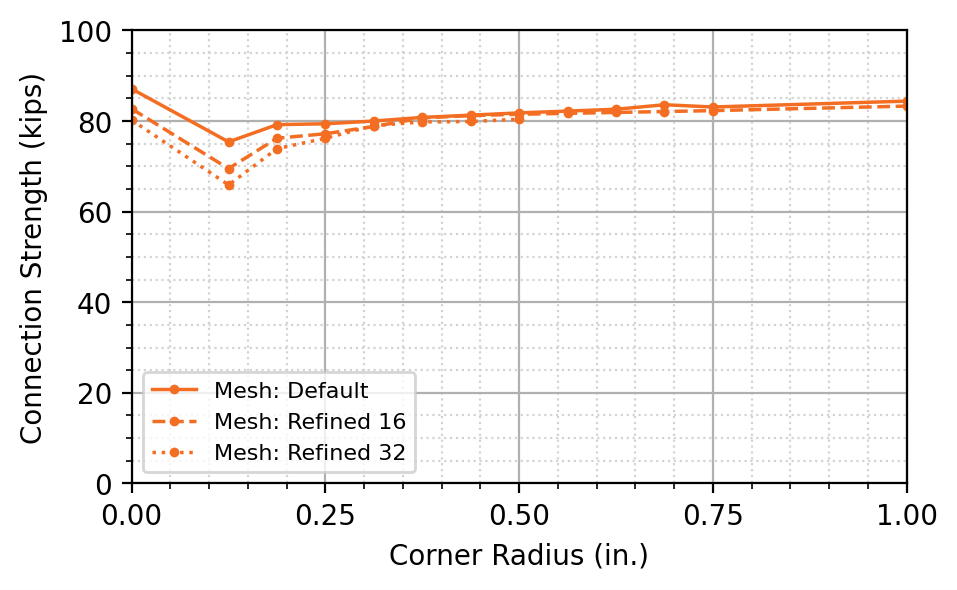
Analyses were performed in IDEA StatiCa on corner radius dimensions varying from 0 to 1 in., using three different mesh sizes. The mesh size was varied in the code setup using the “number of elements on the biggest member web or flange” option. To evaluate the effect of mesh size on the design strength, the default setting of 8 elements was first tested. Two additional tests were performed using values of 16 and 32 elements. Figure 9 shows plastic strain distributions for rounding radius dimensions of 0, 1/8, and 1/2 in. for mesh options of 8, 16, and 32 elements. The maximum factored shear load that can be applied to the connection is presented in Figure 10.
For the three mesh sizes tested, the cope with a square reentrant corner (rounding radius = 0 in.) presented the greatest connection strength. Introducing a small radius of 1/8 in. caused a decrease in strength. The strength then increased with an increasing radius up to 1/2 in., and beyond 1/2 in. remained constant with minimal increase. The IDEA StatiCa mesh size had little effect on the connection strength with rounding radius dimensions beyond 3/8 in.
With a coarser mesh and small (but not zero) radius, elements at the corner become badly shaped (long skinny triangles) as seen in Figure 9 since the algorithm that creates the mesh in IDEA StatiCa currently uses 3 segments in the radius regardless of the size of the radius or typical elements.
Using an appropriate reentrant corner radius (e.g., 3/8 to 1/2 in. for statically loaded connections as stated in the user note in AISC Specification Section M2.2) and modeling the corner radius as designed in IDEA StatiCa is likely the best approach and one that will work with the default mesh settings.
Figure 9 Plastic strain distributions for varying radius dimensions and mesh sizes
Figure 10 Connection strength from IDEA StatiCa vs reentrant corner radius
Effect of Position of Applied Force
Part 9 of the AISC Manual defines the force eccentricity, e, as the “distance from the face of the supporting member to the face of the cope, unless a lower value can be justified” essentially designating the face of the supporting member as the point of zero moment or the “pin”. IDEA StatiCa allows for the position of the applied force to be manually adjusted. The position of applied force can be used to define the point of zero moment. For all analyses in this report except for those described in this section, the position of the applied force was set equal to half of the girder web thickness from the node (i.e., the face of the supporting member). Given that even simple shear connections have some rotational restraint the actual location of the point of zero moment will depend on the relative stiffness of the beam, connection, and support.
IDEA StatiCa also allows the user to select between four model types when specifying members:
- N-Vy-Vz-Mx-My-Mz
- N-Vz-My
- N-Vy-Mz
- N-Vy-Vz
The model type designation refers to the types of forces that can be applied to the member, with all other degrees of freedom restrained. To evaluate the effect of the position of applied shear force on the design strength of the coped beam connection, the model types N-Vy-Vz-Mx-My-Mz and N-Vy-Vz were analyzed.
Analyses were performed on an all-bolted double angle connection and a bolted/welded shear end plate connection. These connection configurations were like those used in the earlier evaluation of strength vs. cope length, with modifications made to ensure limit states related to the coped beam web controlled. For the all-bolted double angle connection, a cope length of 10 in. was used, the girder profile was increased to a W21x101, the double angle profile was increased to an L5x5x1/2 (ASTM A529 Gr 55) of length 10 in., and the bolt diameter was increased to 1 in., with 3 bolts spaced at 3 in. on center and a 2-in. edge distance on the top and bottom. For the bolted/welded shear end plate connection, a cope length of 7-1/2 in. was used, and the weld size was increased to 1/2 in.
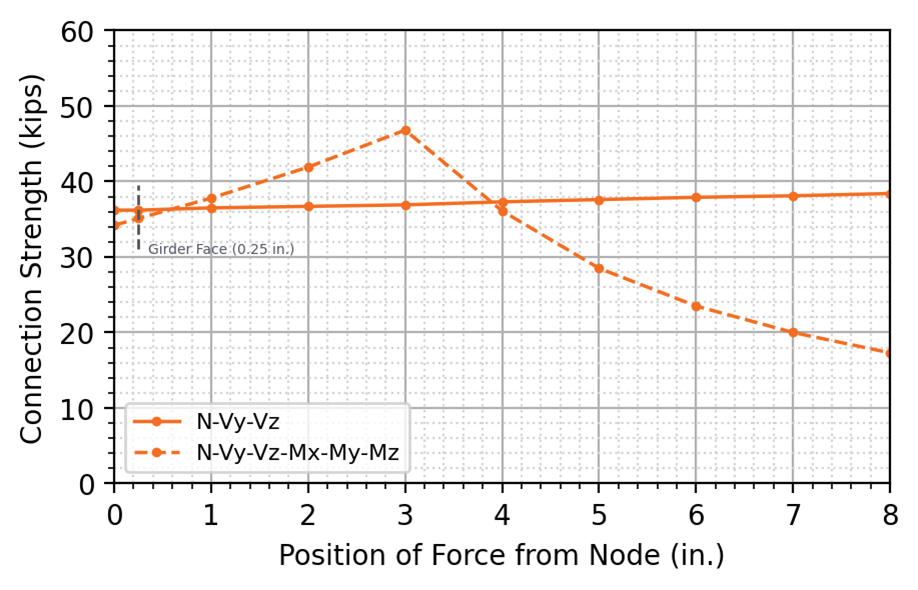
The connection strength as a function of the position of applied force from the node is shown for the all-bolted double angle connection in Figure 11 and for the bolted/welded shear end plate connection in Figure 12.
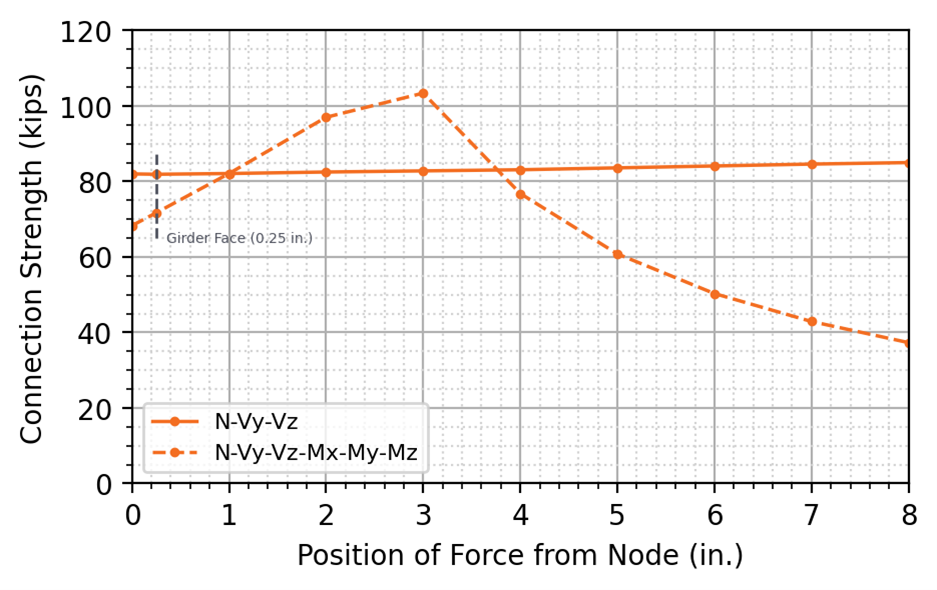
For both the all-bolted double angle and bolted/welded shear end plate connections, the design strength for model type N-Vy-Vz remained nearly level with a slight increase in strength as the position of applied force increased beyond 3 in. from the node. The buckling ratio limit of 3.0 controlled all tests for model type N-Vy-Vz. When using a N-Vy-Vz model type, the rotation at the end of the member away from the connection is restrained and a moment reaction develops. For this connection, use of the N-Vy-Vz model type largely nullifies the selection of the location of applied force. The moments in the beam (including the point of zero moment) result from the relative stiffness of the beam, connection, and girder.
For model type N-Vy-Vz-Mx-My-Mz, both connection configurations presented increasing design strength with increases in the position of applied force from the node up to 3 in., after which the design strength sharply decreased with increasing distance from the node. For the all-bolted double angle connection, the 5% plastic strain limit controlled for positions of applied force up to 3 in. from the node, after which plastic strain in the double angle cleat controlled the design strength. For the bolted/welded shear end plate, the 3.0 buckling ratio limit controlled for positions of applied force up to 3 in. from the node, after which the strength of the welds controlled the design strength. As the position of force from the node increases, the moment at the critical section for flexural local web buckling decreases allowing more load. However, at the same time, the moment at the connection increases with the demands on the connection eventually controlling.
The N-Vy-Vz model type may be considered as more physically accurate for some beam lengths since the point of zero moment arises naturally from the relative stiffness of the beam, connection, and girder, instead of being assumed. The difference in connection strength between the two models is 14% for the all-bolted double angle connection and 3% for the bolted/welded shear end plate connection when the position of force is defined at the face of the support with the N-Vy-Vz model type giving greater connection strength in both cases.
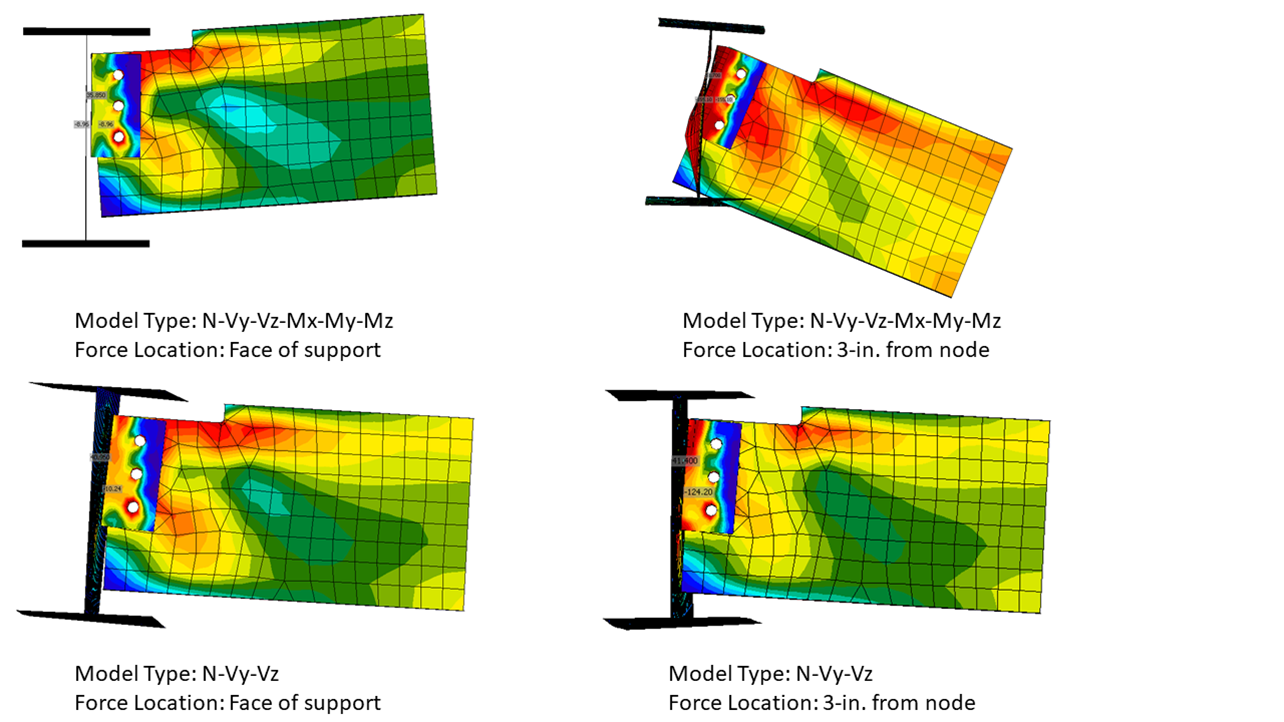
The deflected shapes for an all-bolted double angle connection for both model types for the cases of the force applied at the face of the support and 3-in. from the node are presented in Figure 13. With the N-Vy-Vz-Mx-My-Mz model type and the force at the face of support, the beam deflects up. While this deformation is not realistic the distribution of forces for this case is most consistent with the assumptions described in Part 9 of the AISC Manual.
Use of assumptions other than point of zero moment being at the face of the support is permitted in design, however, the moment on the supporting member (which increases as the point of zero moment shifts away from the face of the support) must be considered when designing the supporting member.
Figure 11 Connection strength from IDEA StatiCa vs position of applied force from node (all-bolted double angle connection)
Figure 12 Connection strength from IDEA StatiCa vs position of applied force from node (bolted/welded shear end plate connection)
Figure 13 Deflected shape comparison for a single coped beam (all-bolted double angle connection). Scale Factor = 3.0.
Double Coped Beams
The design strength of double coped beams was evaluated against varying dimensions of cope length and cope depth, with an equal length cope at the bottom and top flange.
AISC Manual Part 9 recommends that the flexural strength of a beam coped at the top and bottom flanges be determined in accordance with AISC Specification Section F11, using a modified lateral-torsional buckling modification factor, Cb. When the bottom cope is equal to or larger than the length of the top cope, Cb is calculated as:
\[C_b=\left [ 3+\ln \left ( \frac{L_b}{d} \right ) \right ] \left ( 1-\frac{d_{ct}}{d} \right ) \ge 1.84 \]
where:
- \(C_b\) – lateral-torsional buckling modification factor
- \(L_b = c_t\)
- \(c_t\) – length of top cope
- \(d\) – depth of beam
- \(d_{ct}\) – cope depth at top flange
Additionally, noting that shear buckling has been observed in experimental tests with slender webs and short copes, Dowswell (2018) recommends that the shear strength of a beam coped at the top and bottom flange be determined according to AISC Specification Section G3, using \(k_v=3.2\), \(\phi=1.00\) and \(A_w=h_0 t_w\). With these modifications, the nominal shear strength, Vn, is calculated as:
\[ V_n=0.6 F_y h_0 t_w C_{v2} \]
where:
- \(C_{v2}\) – web shear buckling strength coefficient, as defined in AISC Specification Section G2.2
- \(h_0\) – depth of the coped section
- \(t_w\) – web thickness
When \(\frac{h_0}{t_w} \le 1.10 \sqrt{ \frac {k_vE}{F_y} }\)
\[C_{v2}=1.0\]
When \( 1.10 \sqrt{ \frac {k_vE}{F_y} } < \frac{h_0}{t_w} \le 1.37 \sqrt{ \frac {k_vE}{F_y} }\)
\[C_{v2} = \frac{1.10 \sqrt{ \frac {k_vE}{F_y} }}{\frac{h_0}{t_w}}\]
When \(\frac{h_0}{t_w} > 1.37 \sqrt{ \frac {k_vE}{F_y} }\)
\[C_{v2}=\frac{1.51 k_v E}{\left ( \frac{h_0}{t_w}\right )^2 F_y}\]
An all-welded double-angle connection was used to evaluate the design strength of a double-coped beam. The limit states specific to the connection include weld rupture, beam web base metal strength at the weld, shear yielding of the angles, shear rupture of the angles, and girder web base metal strength at the weld. These limit states, along with lateral-torsional buckling, flexural yielding, shear yielding, shear rupture, and shear buckling of the double-coped beam web were evaluated, and the design strength of the connection was compared to the results of the CBFEM analysis performed in IDEA StatiCa.
Strength vs Cope Length
For this investigation, an initial coped beam configuration was chosen to match that of Example II.A-7 of the AISC Design Examples v15.1 (AISC, 2019). The girder is a W21x101 with a reduced flange width to accommodate shorter cope lengths. The double angle profile is that of an L3-1/2x3x1/2 with length 8 in. and conforming to ASTM A529 Gr 50 (Fy = 50 ksi and Fu = 65 ksi). The fillet welds on the beam and girder side are 3/16 in. and 3/8 in., respectively. Figure 14 presents a three-dimensional view of the connection.
Figure 14 Three-dimensional view of the double coped beam connection
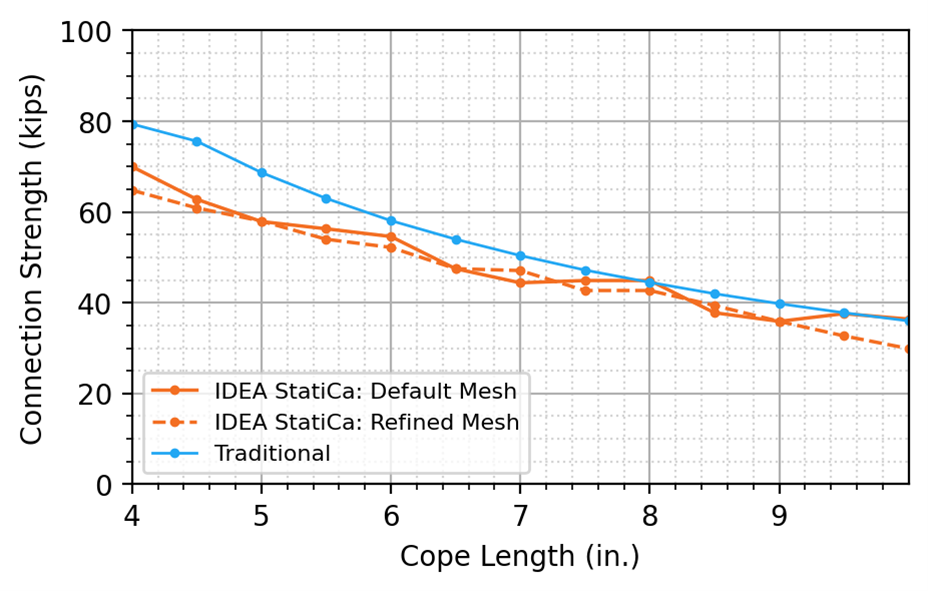
Calculations were performed on 13 different cope lengths ranging from 4 to 10 in. in 1/2 in. increments. The maximum factored shear load that can be applied to the connection (i.e., the connection strength) is presented in Figure 15. As expected, for both the traditional calculation results and the IDEA StatiCa results, the design strength decreases with increasing cope length. For the traditional calculations, the weld strength at the support controlled for the initial cope length of 4 in., beyond which lateral-torsional buckling of the beam web controlled the design strength. For IDEA StatiCa, the 5% plastic strain limit of the beam web controlled all cope lengths up to 9-1/2 in., and the 3.0 buckling ratio limit controlled for the 10 in. cope length. As with the single cope connections, the IDEA StatiCa strength is less than or equal to the strength from the traditional calculations over the range of lengths investigated.
The variation of connection strength with cope length from IDEA StatiCa shown in Figure 15 is not smooth and in some instances the strength increases with cope length. This unexpected behavior could be due to mesh effects. Using a refined mesh (16 elements on the biggest member web or flange) the results are smoother, but not appreciably different from those using the default mesh.
Figure 15 Connection strength vs cope length for a double coped beam
Shear Buckling – Strength vs Cope Depth
To investigate the limit state of shear buckling, a W18x35 beam was modified to have a depth of 24 in., presenting a more slender web for the analysis. A W24x104 girder was used, with the flange width modified to accommodate a shorter beam cope length, and the L3-1/2x3x1/2 double angle was increased to have a length of 14 in.
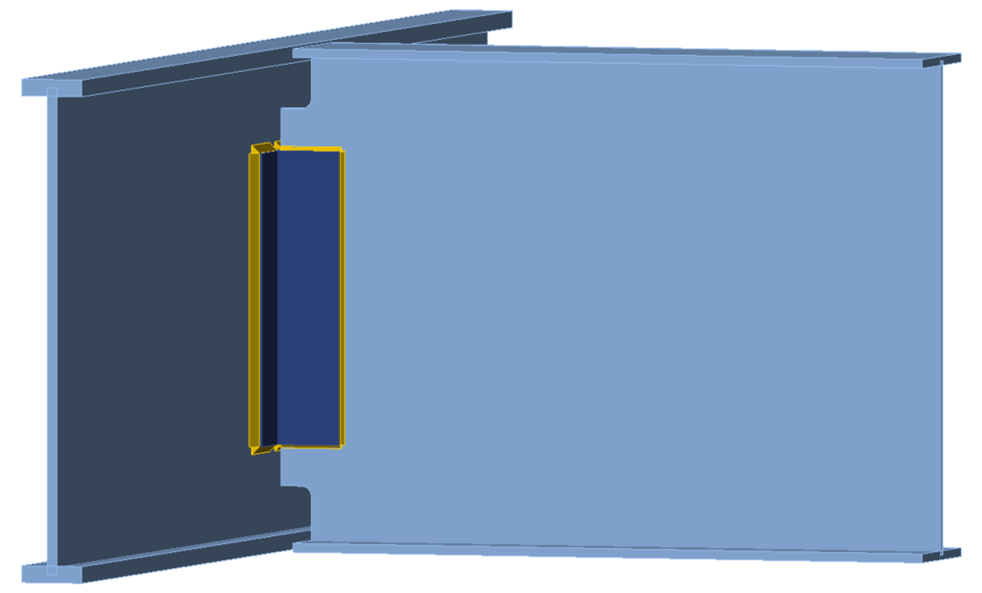
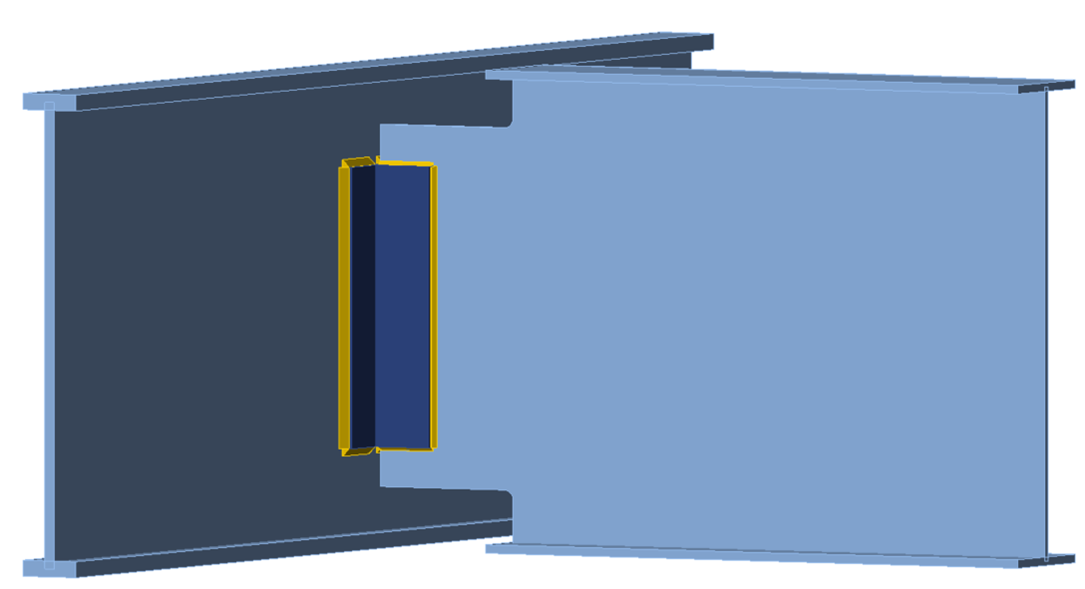
Cope lengths of 1-1/2 in. and 7-1/2 in. were evaluated with varying cope depths to identify cope configurations where shear buckling controlled for the traditional calculations. These results were compared to the results of the CBFEM analysis from IDEA StatiCa. Figure 16 and Figure 17 present three-dimensional views of the connections with 1-1/2 in. and 7-1/2 in. cope lengths, respectively.
Figure 16 Three-dimensional view of double coped beam with a deep web (1.5 in. cope length)
Figure 17 Three-dimensional view of double-coped beam with a deep web (7.5 in. cope length)
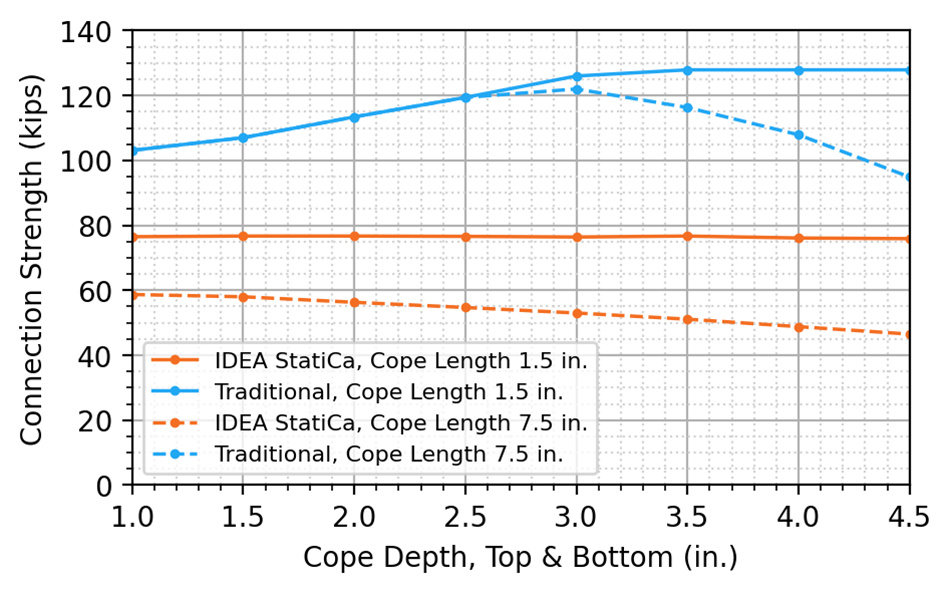
Calculations were performed on 8 different cope depths ranging from 1 to 4.5 in. in 1/2 in. increments. The maximum factored shear load that can be applied to the connection is presented in Figure 18.
For the traditional calculations, the limit state of shear buckling controlled for all cope depths for the 1-1/2 in. cope length. For the 7-1/2 in. cope length, shear buckling controlled for cope depths up to and including 2-1/2 in., beyond which lateral-torsional buckling of the beam web controlled. The initial increase in connection strength associated with deeper top and bottom copes (i.e., less material) is due to the reduced slenderness of the coped section resulting in an increased web shear buckling strength coefficient, Cv2. However, Cv2 remains below the upper limit of 1.0 where shear yielding would begin to control. For the longer cope length of 7-1/2 in., lateral-torsional buckling begins to control beyond cope depths of 2-1/2 in., resulting in a reduced connection strength with increased cope depth.
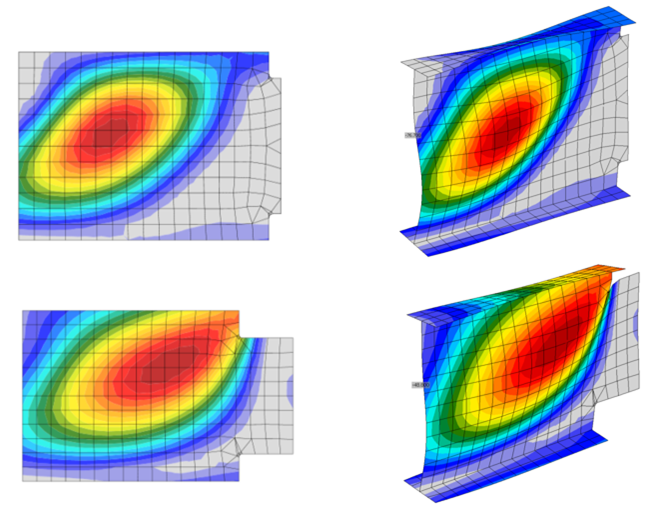
For IDEA StatiCa, the 3.0 buckling ratio limit controlled for all cope depths for both the 1-1/2 in. and 7-1/2 in. cope lengths. For the 1-1/2 in. cope length, the connection strength remains constant whereas the 7-1/2 in. cope length presents a decrease in connection strength as cope depth increases. This is because the buckling of the coped beam web occurs completely outside of the coped section for the 1-1/2 in. cope length, whereas for the 7-1/2 in. cope length, some buckling occurs within the coped section. Figure 19 shows the buckled shape and stress distributions for the two cases. They are consistent with depictions of shear buckling presented by Dowswell (2018). The connection strength is lower for IDEA StatiCa than for the traditional calculations for the entire range of cope depths investigated.
Figure 18 Connection strength vs cope depth for a double coped beam
Figure 19 Buckled shape for 1-1/2 in. and 7-1/2 in. cope lengths (cope depth 3-1/2 in.)
Summary
This study compared the design of beam copes by traditional calculation methods used in US practice and IDEA StatiCa. Key observations from the study include:
- IDEA StatiCa was observed to be conservative in comparison to the traditional calculations for the limit states associated with beam copes, especially the buckling limit states. The buckling ratio limit used in this study was 3.0.
- Using an appropriate reentrant corner radius (e.g., 3/8 to 1/2 in. for statically loaded connections as stated in the user note in AISC Specification Section M2.2) and modeling the corner radius as designed in IDEA StatiCa will avoid generation of badly shaped mesh elements.
- The position of applied force needs to be set to the face of the web support to be consistent with assumptions in the AISC Manual. However, other assumptions may be appropriate for design.
References
- AISC. (2016). Specification for Structural Steel Buildings. American Institute of Steel Construction, Chicago, Illinois.
- AISC. (2017). Steel Construction Manual, 15th Edition. American Institute of Steel Construction, Chicago, Illinois.
- AISC (2019). Steel Construction Manual Design Examples, v15.1. American Institute of Steel Construction, Chicago, Illinois.
- Dowswell, B. (2018). “Designing Beam Copes.” Modern Steel Construction, AISC. (February), 16-21.