Vorspannung in Detail - Vorspannung mit sofortigem Verbund
Einleitung und Annahmen
Lassen Sie uns zunächst mit einer kurzen Beschreibung unserer Betonbemessungssoftware beginnen. In diesem Artikel geht es hauptsächlich um die Spannbetonbemessung in Detail, das im Allgemeinen für die Bemessung von Diskontinuitätsbereichen oder für die Bemessung von Bauteilen mit Diskontinuitätsbereichen wie Öffnungen, gestuften Enden usw. entwickelt wurde.
Für den Vergleich der Ergebnisse werden wir Beam verwenden, dessen Zweck, wie der Name schon sagt, die Bemessung von Betonträgern ist.
Zweitens müssen wir einige Annahmen und Einschränkungen definieren, um die Bemessung von Spannbetonträgern in Detail besser zu verstehen.
- Die zeitabhängige Analyse (TDA - Time Depended Analysis) ist in Detail nicht implementiert. Andererseits ist die TDA in Beam für die Bemessung von Spannbetonträgern implementiert.
- TDA kann in Detail unter Verwendung des Kriechkoeffizienten und der Inkremente simuliert werden.
- Schwinden und Temperaturbelastungen sind im Detail nicht implementiert, diese sind aber für kommende Versionen in Planung.
Inkremente
Bevor wir das Beispiel durchgehen, müssen wir verstehen, wie die Inkremente für die Spannbetonbemessung in Detail funktionieren.
Es gibt 3 Lastarten, die in Detail in drei Stufen auf das Modell angewendet werden.
- Vorspannung - für Inkrement P
- Ständig - für Inkrement G
- Variabel - für Inkrement V
Wenn Sie eine Lastfallkombination erstellen wird der gesamte Anteil der Vorspannung im ersten Inkrement P, der gesamte Anteil des ständigen Lastfalls im zweiten Inkrement G und der gesamte Anteil des variablen Lastfalls im dritten Inkrement V aufgebracht.
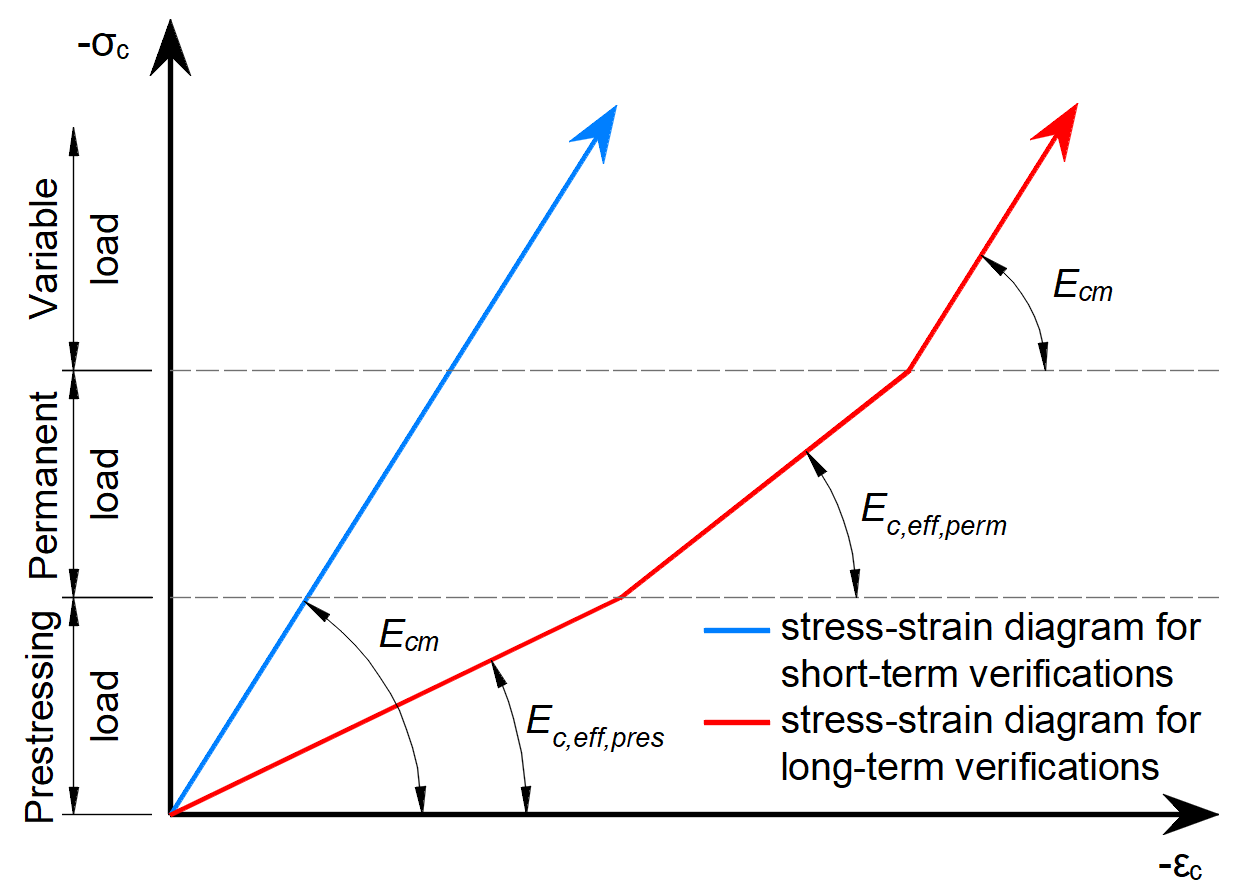
Der Grund für die Inkremente ist, dass für GZG-Nachweise verschiedene Materialmodelle verwendet werden.
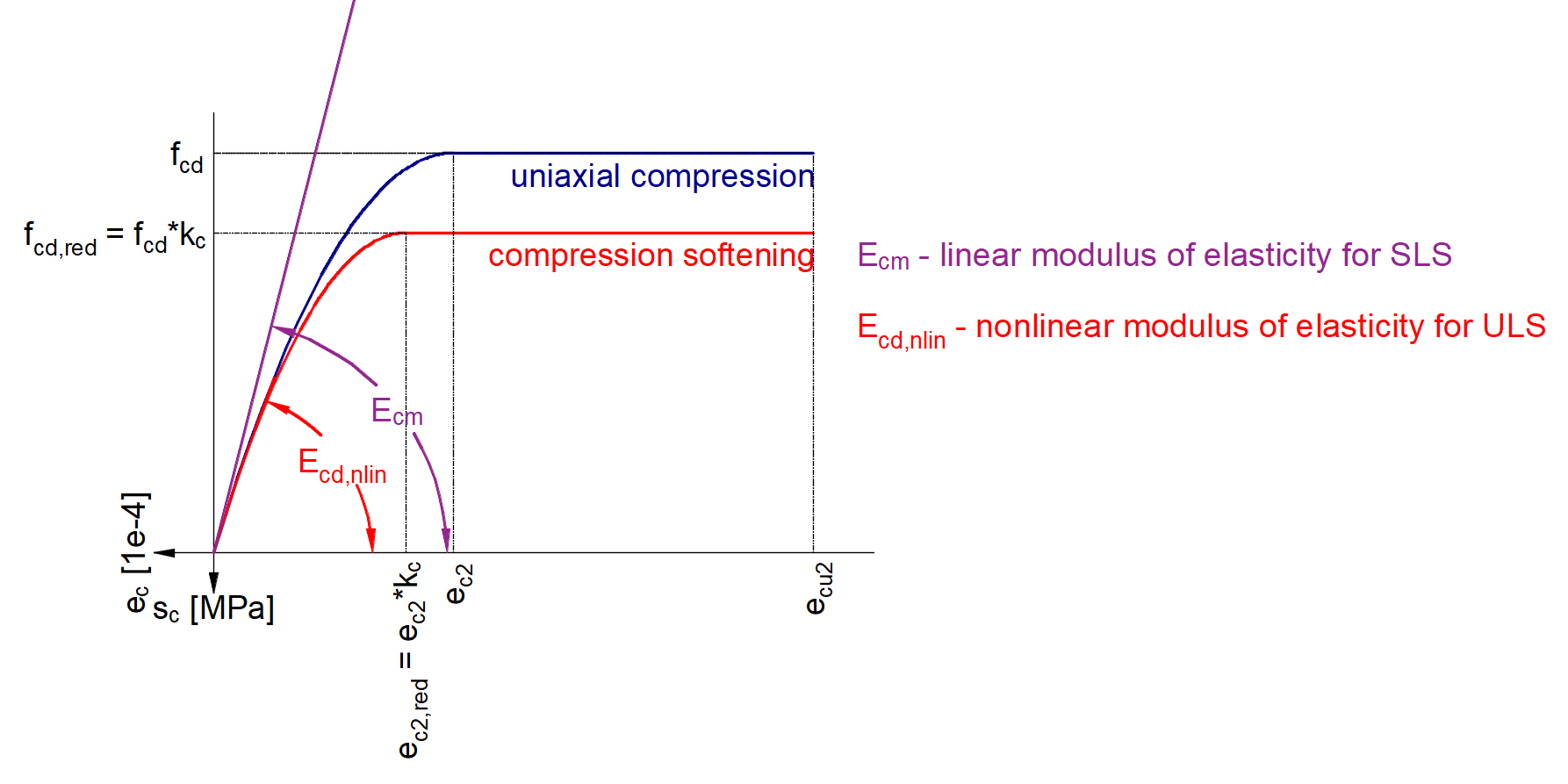
Wie Sie sehen können, gibt es drei Elastizitätsmodule:
- Ec,eff,press = Ecm / (1+φpress) - Effektiver Elastizitätsmodul des Betons für das P-Inkrement
- Ec,eff,perm = Ecm / (1+φperm) - Effektiver Elastizitätsmodul des Betons für das G-Inkrement
- Ecm - Sekantenmodul von Beton
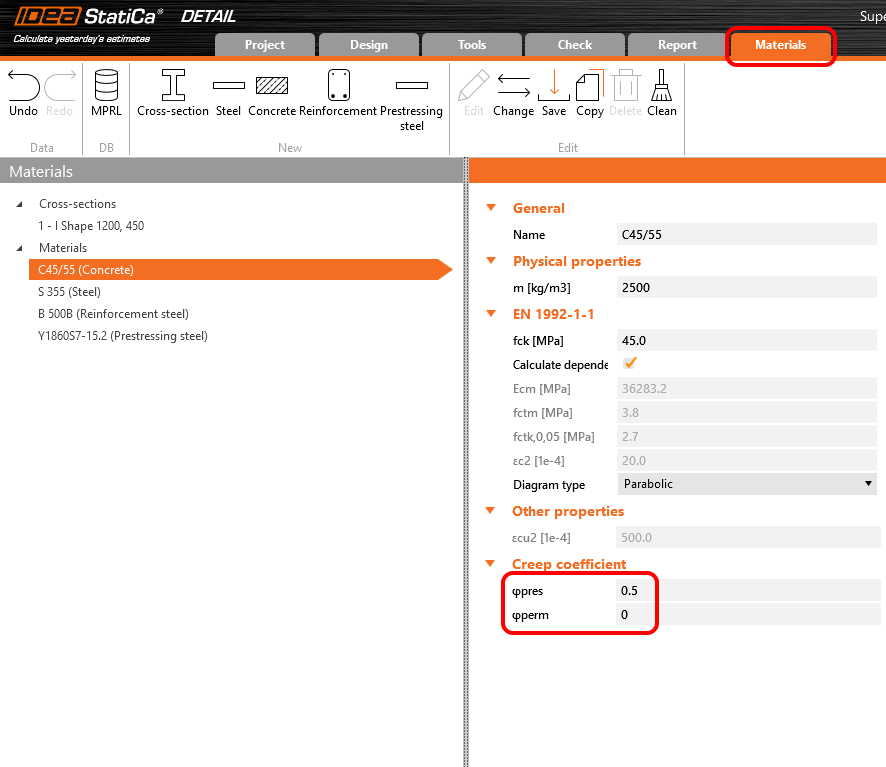
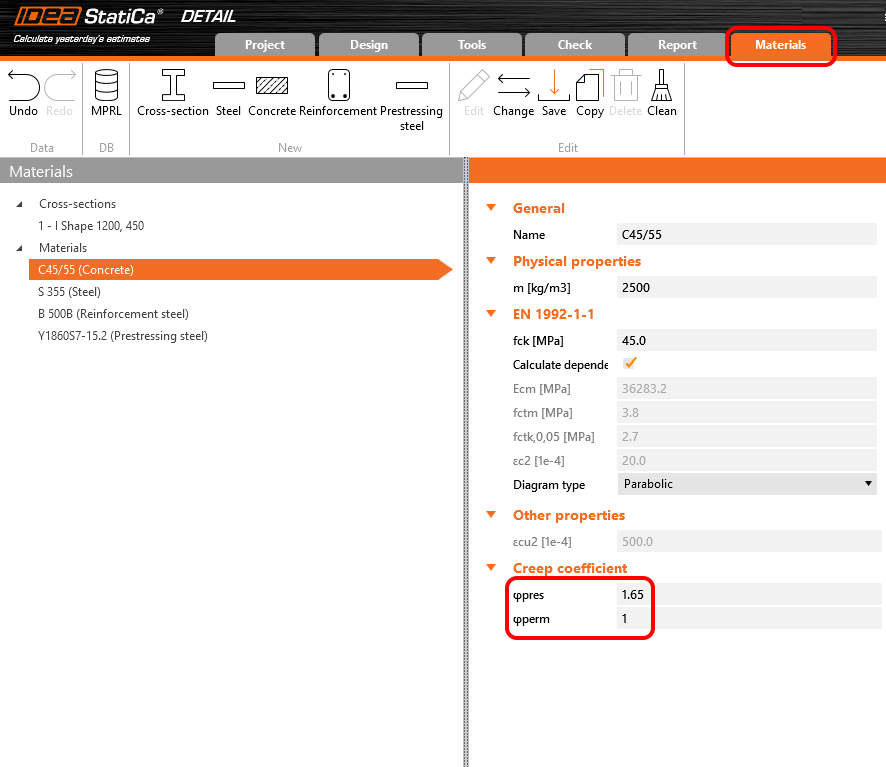
Dabei sind φpress und φperm die Kriechkoeffizienten für die P- und G-Inkremente. Die Koeffizienten können in Materialien & Modelle eingestellt werden.
Bitte beachten Sie, dass für Kurzzeiteffekte nur Ecm verwendet wird. Er gilt für alle drei Inkremente. Und der langfristige Verlust wird nur bei Langzeiteffekten berücksichtigt.
Die Parameter des Trägers
Zwei identische Modelle werden in Beam und Detail erstellt. Sie sind am Ende dieses Artikels beigefügt. Laden Sie diese herunter und gehen Sie sie durch, während Sie den Artikel lesen.
Das Beispiel eines Betonträgers wird in Beam vorgestellt und dann wird der Vergleich mit Detail für drei Bauabschnitte durchgeführt.
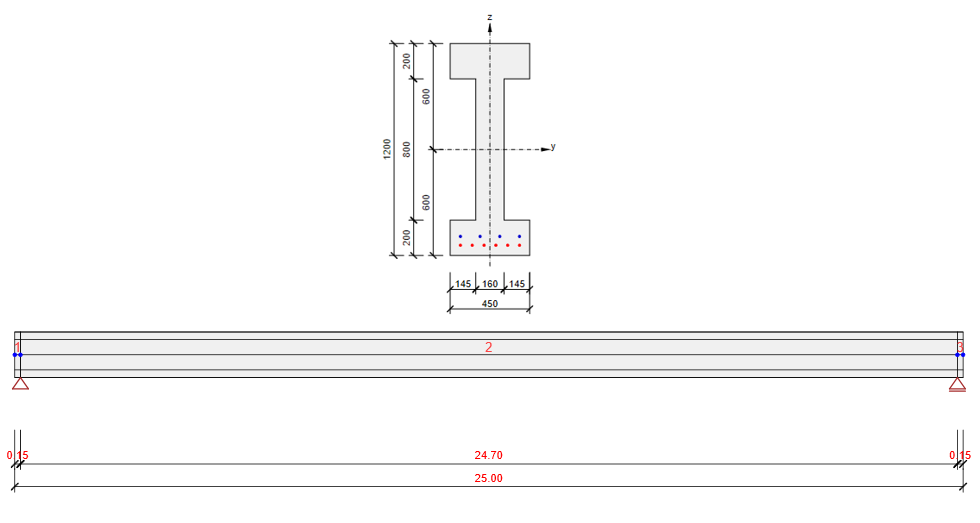
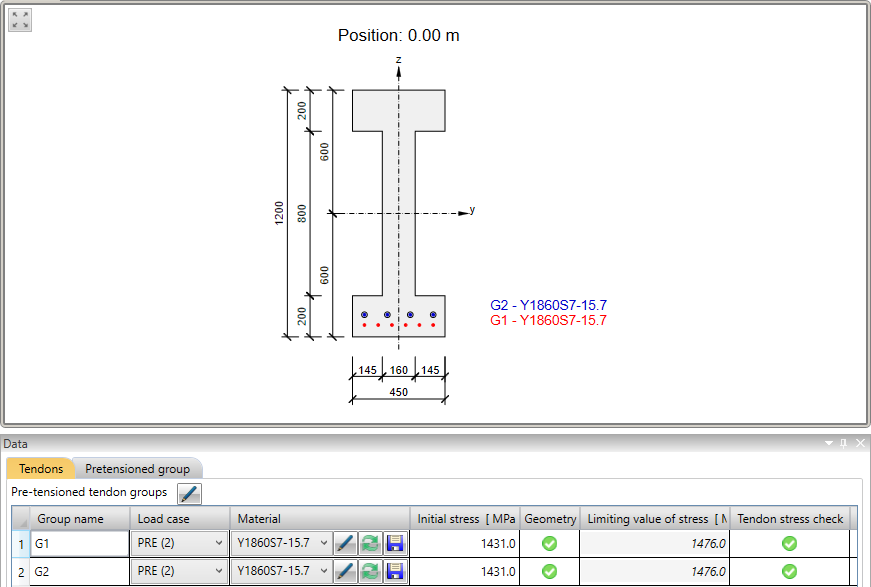
Das Beispiel ist ein Einfeldträger mit I-Querschnitt aus Beton C45/50 und sofortigem Verbund.
Wir werden den Balken in drei Bauphasen nachweisen:
- Übertragung der Vorspannung - 2 d (kurz nach dem Lösen)
- Auflast - 60 d (Beginn der Bemessungsnutzungsdauer)
- Ende der Bemessungsnutzungsdauer- 18250 d (50 Jahre)
Die anderen Phasen können in ähnlicher Weise durchgeführt werden.
Sie werden feststellen, dass wir den benutzerdefinierten Betonmodul verwendet haben. Lesen Sie mehr in: Wie wird der Druckfestigkeitswert von Beton in einer Bauphase eingegeben?. Das liegt daran, dass wir zeigen wollen, wie man einen vorgespannten Träger für ein Betonalter unter 28 Tagen modelliert.
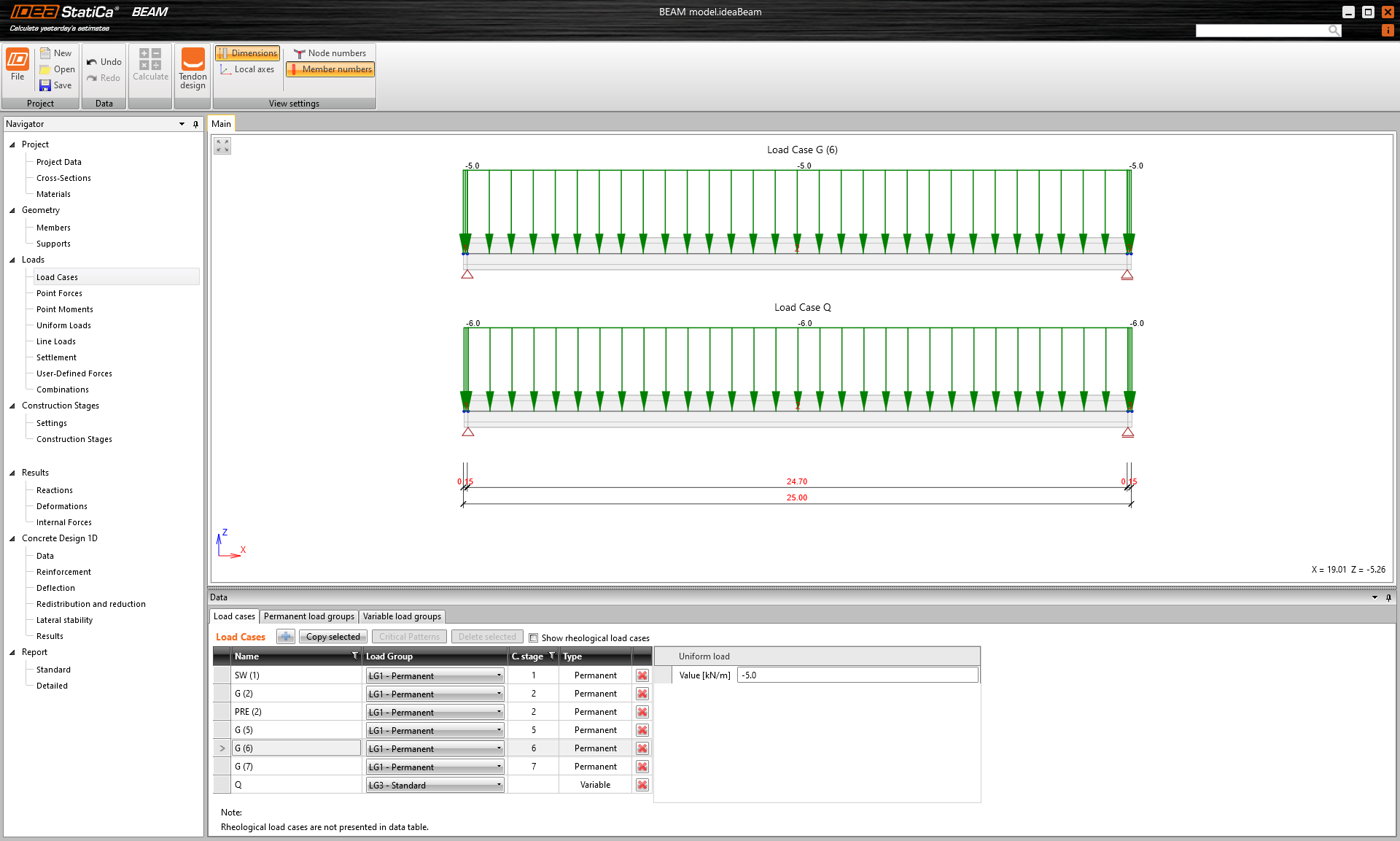
Es werden nur vier Lastfälle eingegeben. Die Zahlen in den Klammern sind die Nummern der Phasen, in denen die einzelnen Lasten aufgebracht werden.
- Eigengewicht - SW (1)
- Vorspannung - PRE (2)
- Ständige Last - G (6)
- Variable Last - Q
Die anderen Lastfälle sind leer.
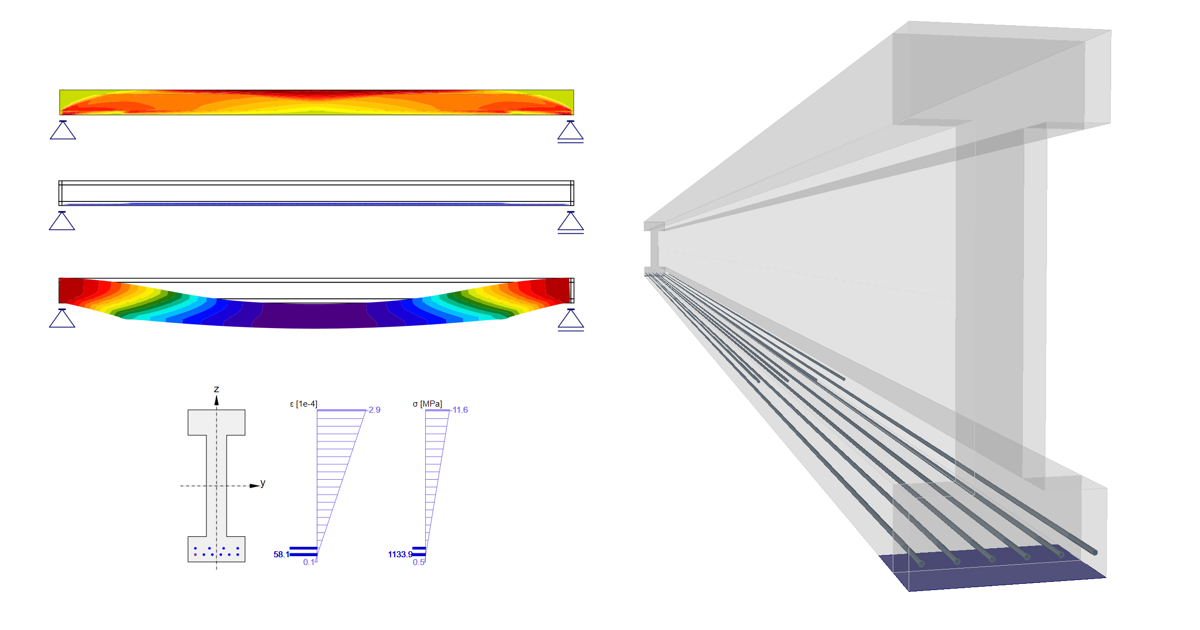
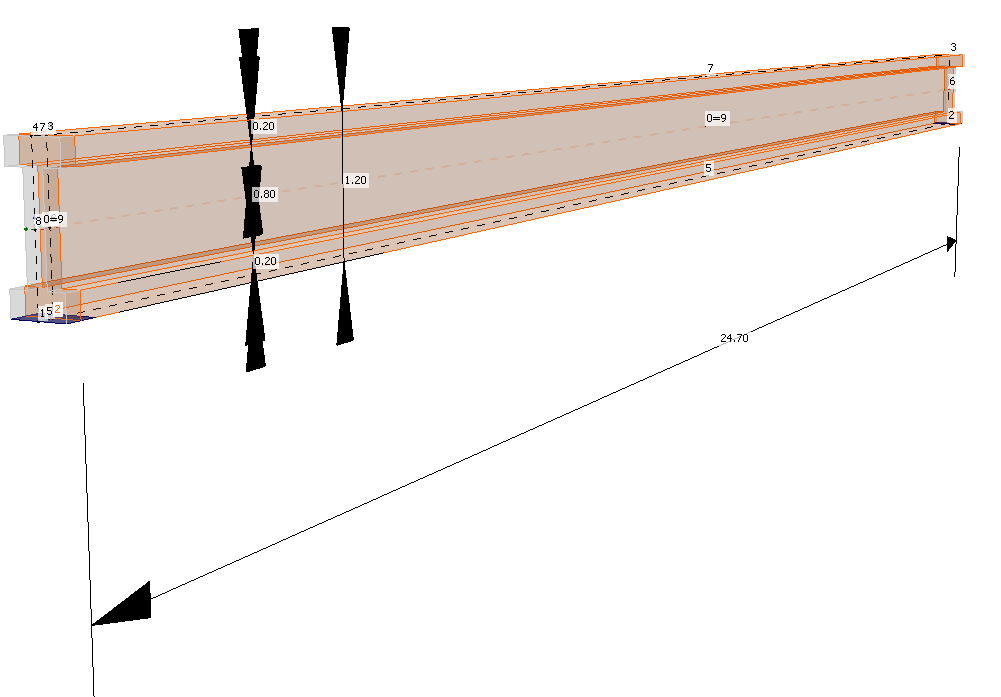
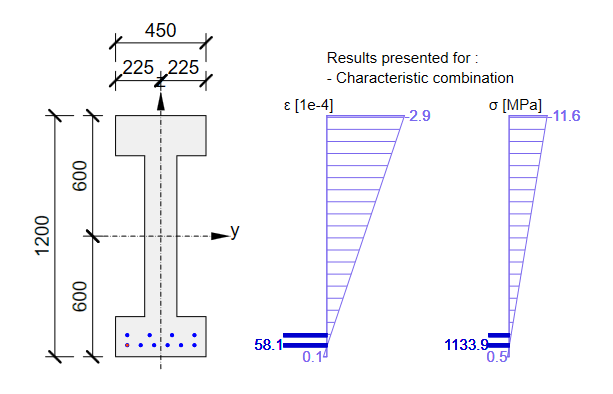
Schauen wir uns nun die Vorspannung an. Es gibt zwei Lagen von Litzen. Es ist erwähnenswert, dass die obere Reihe eine überdeckte Länge von 3,0 m hat.
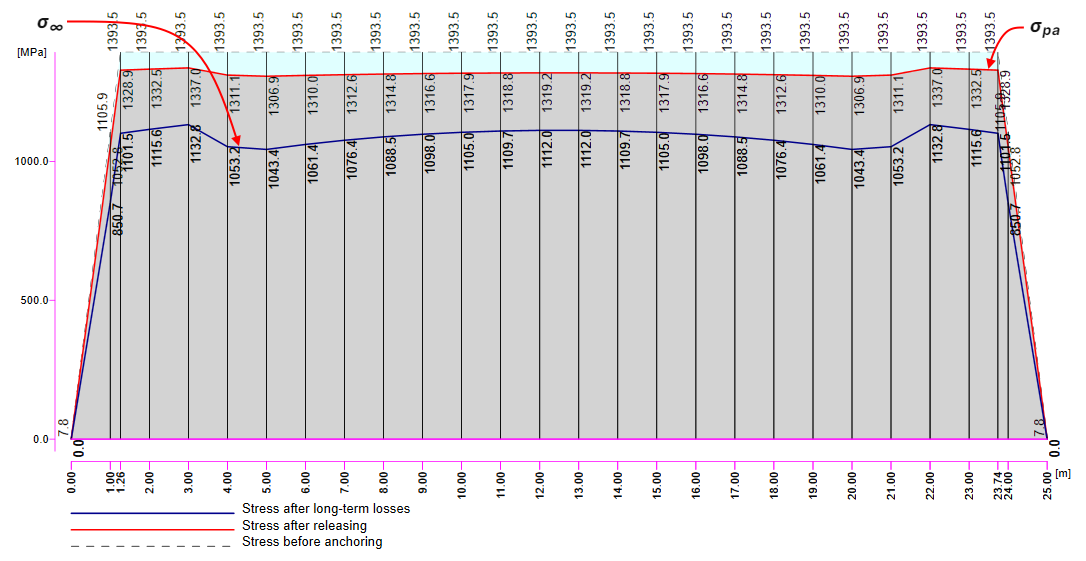
In der nächsten Abbildung sehen Sie die Vorspannungsverluste .
Vorspannung mit sofortigem Verbund (Spannbettvorspannung)
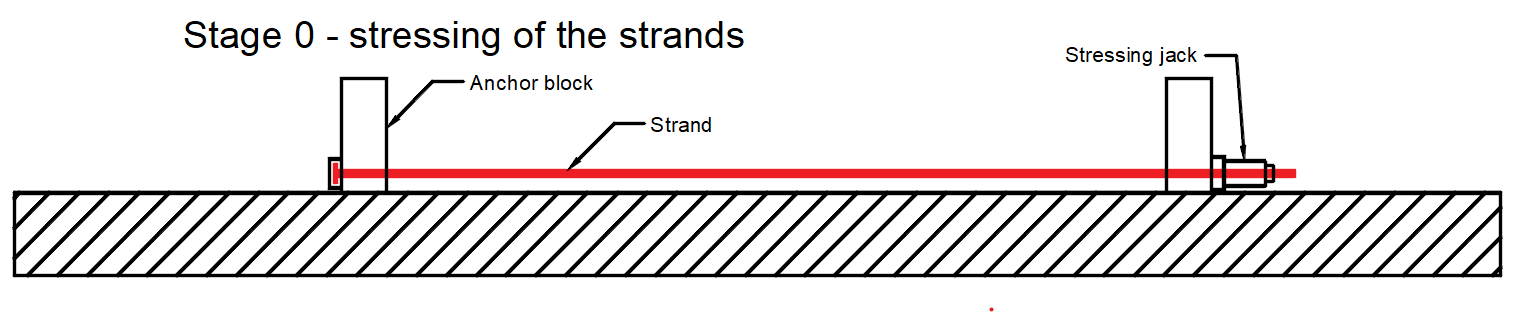
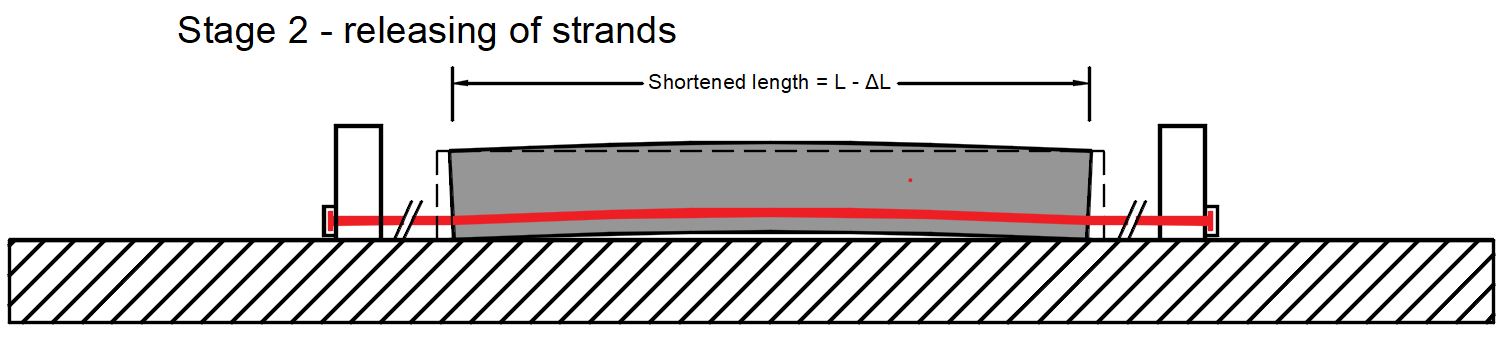
Phase 0 - Spannen der Litzen -> Die Litzen werden in ihrer Position vorbereitet, auf einer Seite verankert und auf der anderen Seite mit einer Spannpresse vorgespannt.
- σp,ini - Anfangsspannung - maximale Spannung während des Spannens. Sie muss gemäß EN 1992-1-1 5.10.2.1 kleiner als σp,max sein. Es handelt sich um die Spannung an der Spannpresse. In unserem Beispiel ist σp,ini = 1431 MPa.
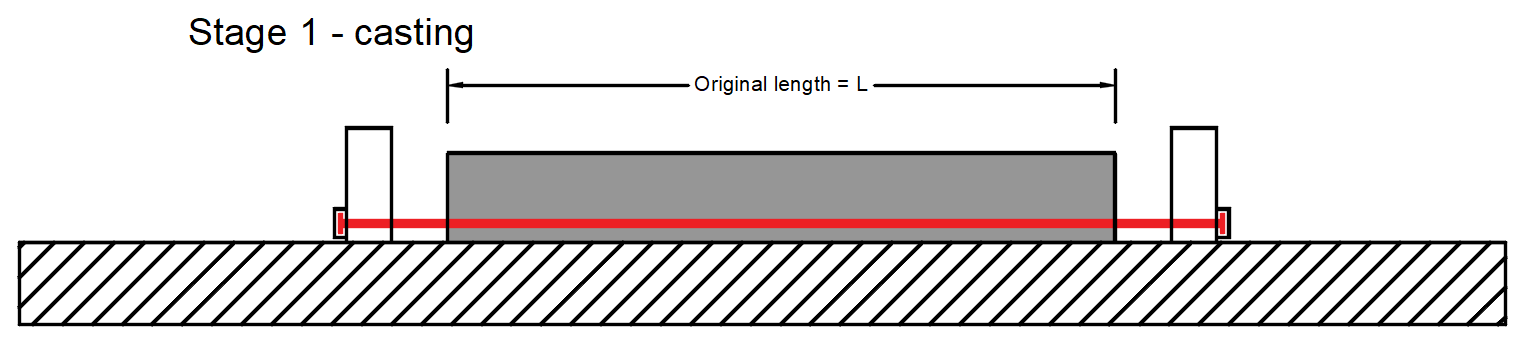
Phase 1 - Gießen -> In dieser Phase wird das Bauteil um die vorgespannten Spannglieder betoniert.
- σpr,cor - Spannung nach kurzzeitiger Entlastung, die auch den Verankerungsverlust und den Verlust durch die Verformung der Widerlager einschließt. In unserem Beispiel σpr,cor = 1415 MPa
Phase 2 - Freigabe der Litzen -> Die Litzen werden losgelassen und die sofortige elastische Betondehnung wird umgesetzt.
- ΔσpT - Verlust aufgrund von Temperaturunterschieden zwischen Spannstahl und Spannbett.
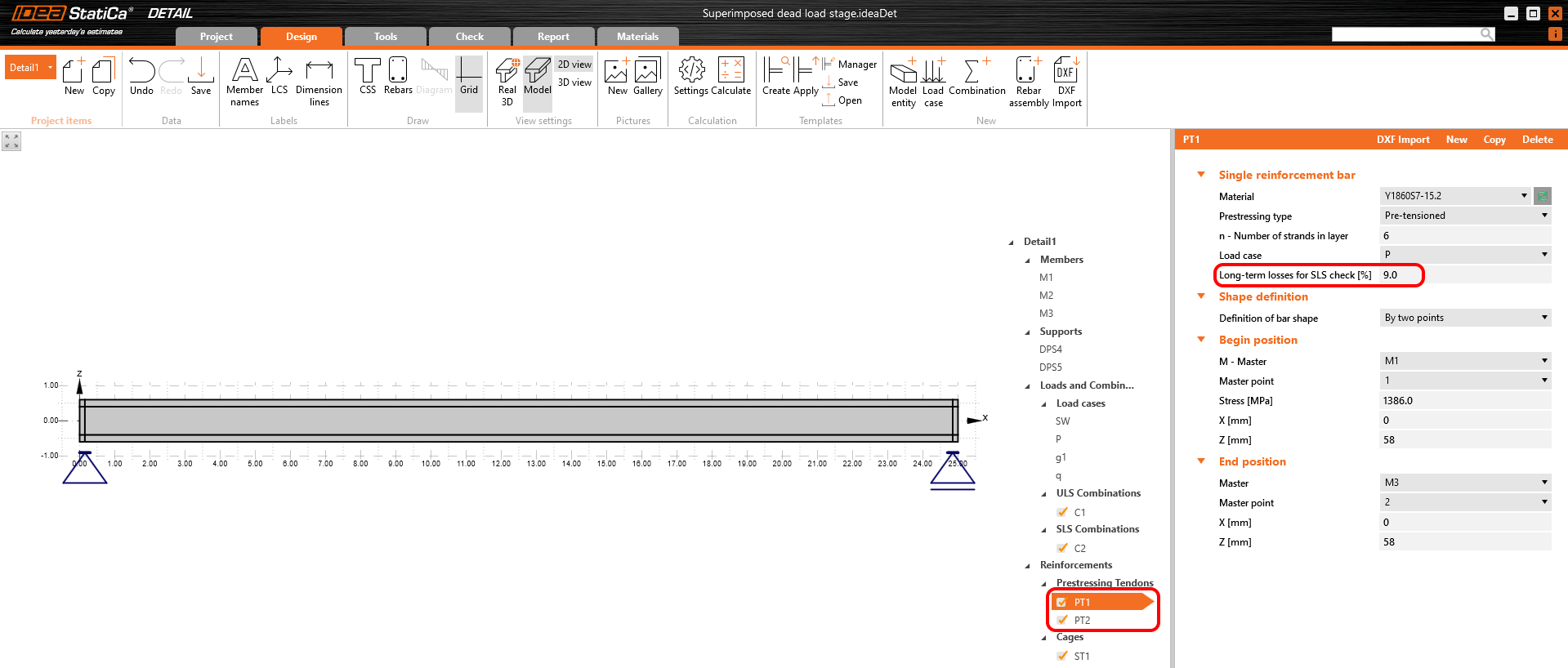
- σpm0 - Spannung kurz vor der Freigabe - Dieser Wert ist die Eingabe für Detail. Es ist auch die Spannung vor dem Verlust durch die unmittelbare elastische Betondehnung - Δσpe. Sie wird berechnet als σpm0 = σpr,cor - ΔσpT. In unserem Beispiel ist σpm0 = 1386 MPa
- Δσpe - Verlust durch unmittelbare elastische Betondehnung.
- σpa - Spannung nach kurzzeitigen Verlusten. Mit anderen Worten, es handelt sich um eine Spannung nach der Übertragung der Vorspannung auf das Bauteil. Sie wird berechnet als σpa = σpr,cor - ΔσpT - Δσpe = σpm0 - Δσpe. In unserem Beispiel ist σpa = 1319.2 MPa
Phase 3 - Ende der Nutzungsdauer
- σ∞ - Spannung nach Langzeitverlusten
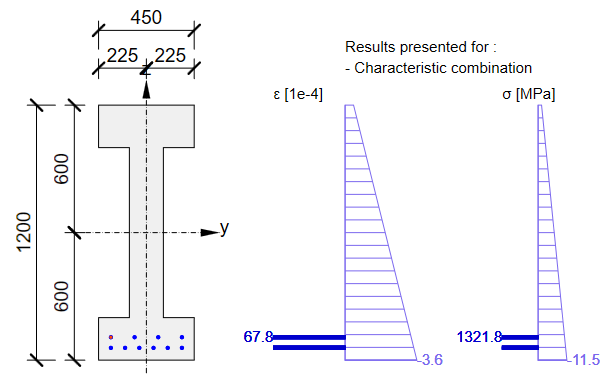
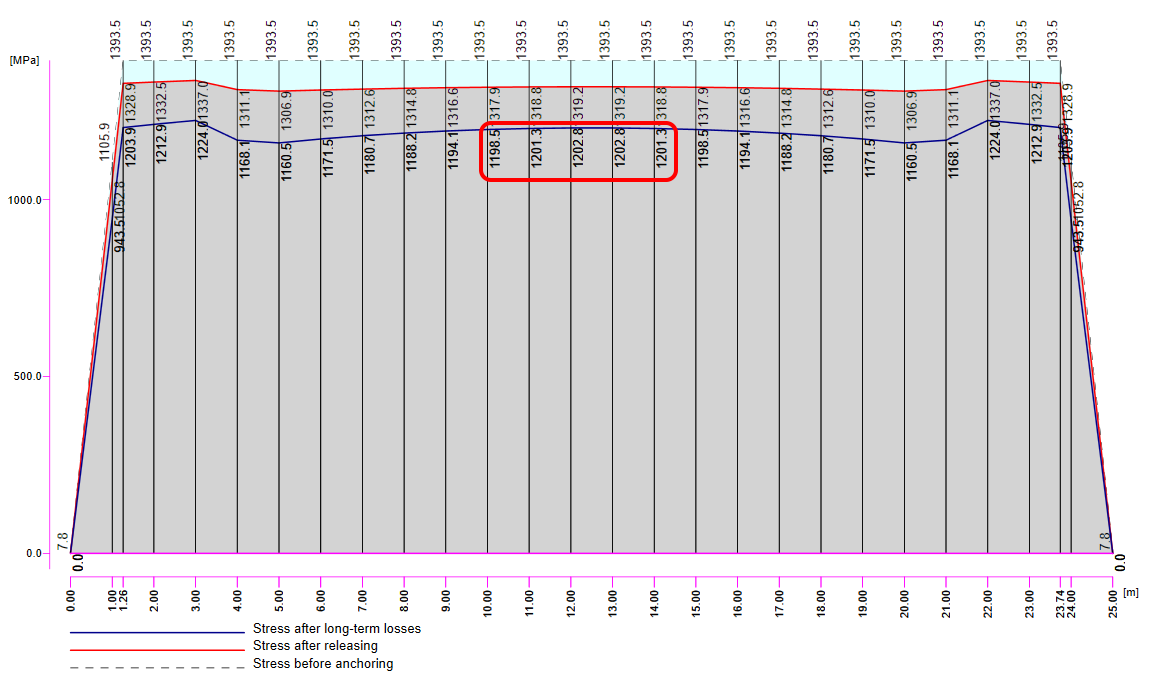
Erinnern Sie sich nun an die obige Abbildung (mit dem Spannungen/Verluste-Diagramm der Spannglieder), in der die Werte von σpa (rote Linie) und σ∞ (blaue Linie) dargestellt sind.
- Lesen Sie mehr: Vorspannen in Detail - Modellbeschreibung
Übertragung der Vorspannung
Das Modell ist definiert. Wechseln wir nun zu Detail und sehen wir uns an, wie wir die erste Phase einstellen. Das Modell ist das gleiche, wir haben nur Bügel für die Scherübertragung hinzugefügt, aber das wird die Ergebnisse nicht beeinflussen.
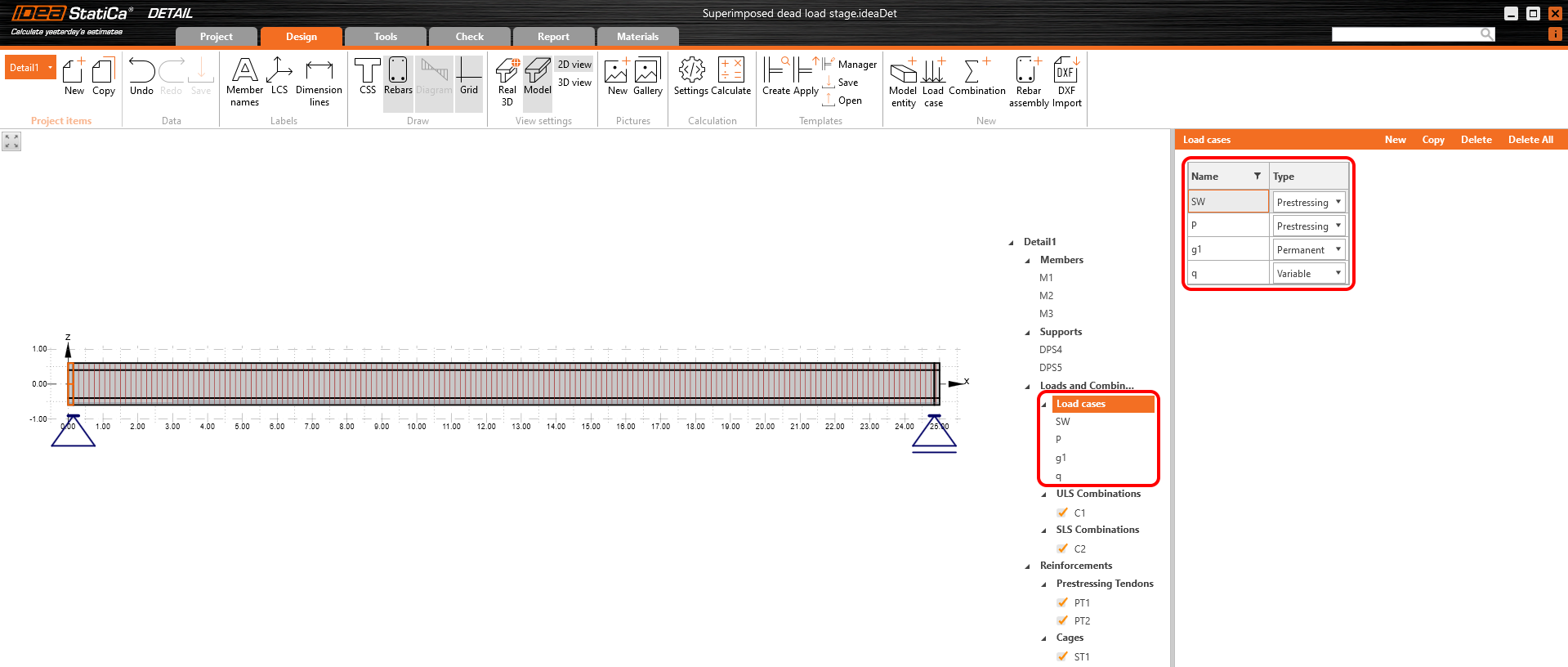
In dieser Phase gibt es nur zwei Lastfälle:
- SW - Vorspannungstyp (Eigengewicht)
- P - Vorspannungsart (Vorspannung)
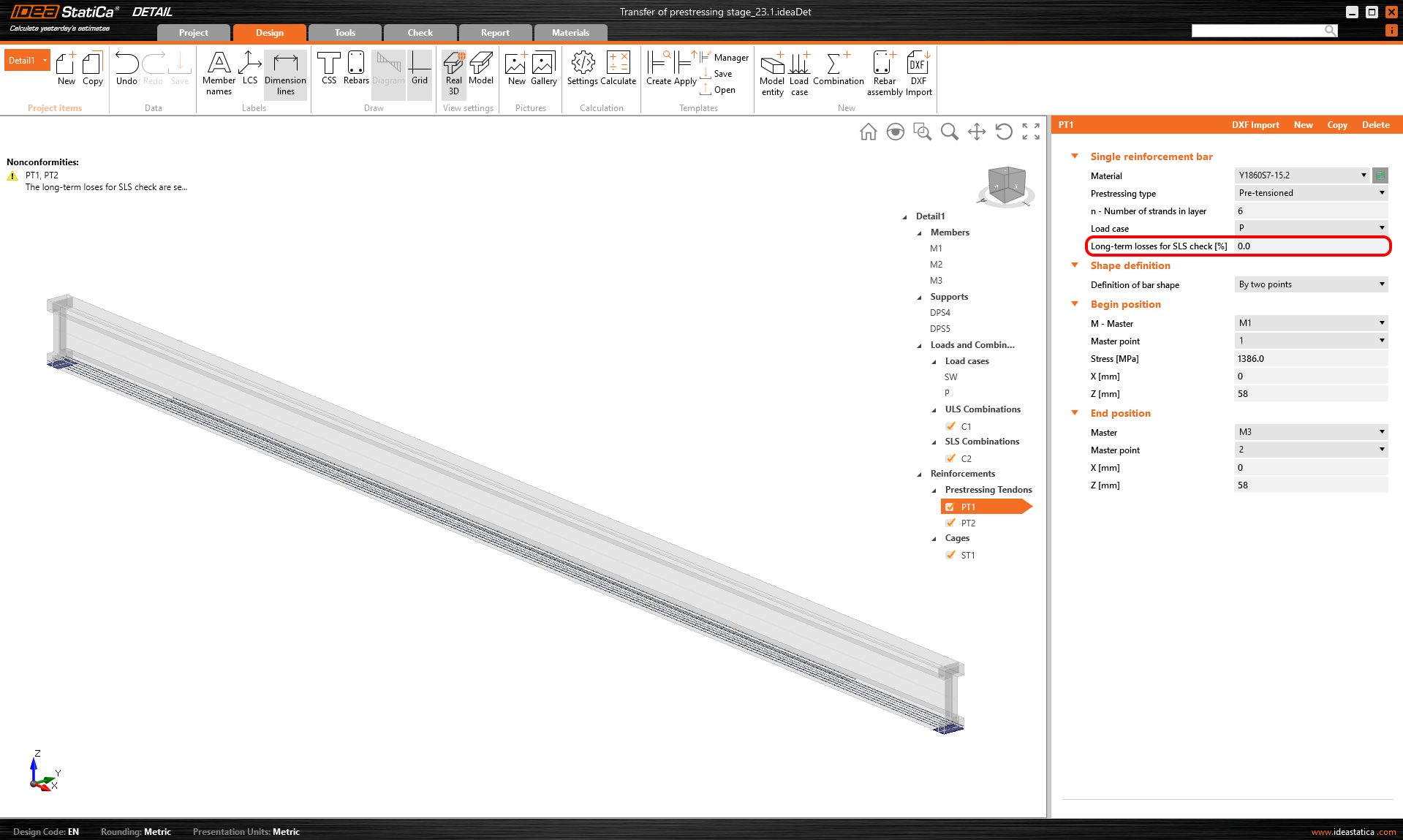
Beide werden im ersten Lastfall angewendet. Wie Sie sehen können, sind die Langzeitverluste für GZG-Nachweise auf 0% eingestellt.
- Lesen Sie mehr: Allgemeine Beschreibung von Lastimpulsen in Detail
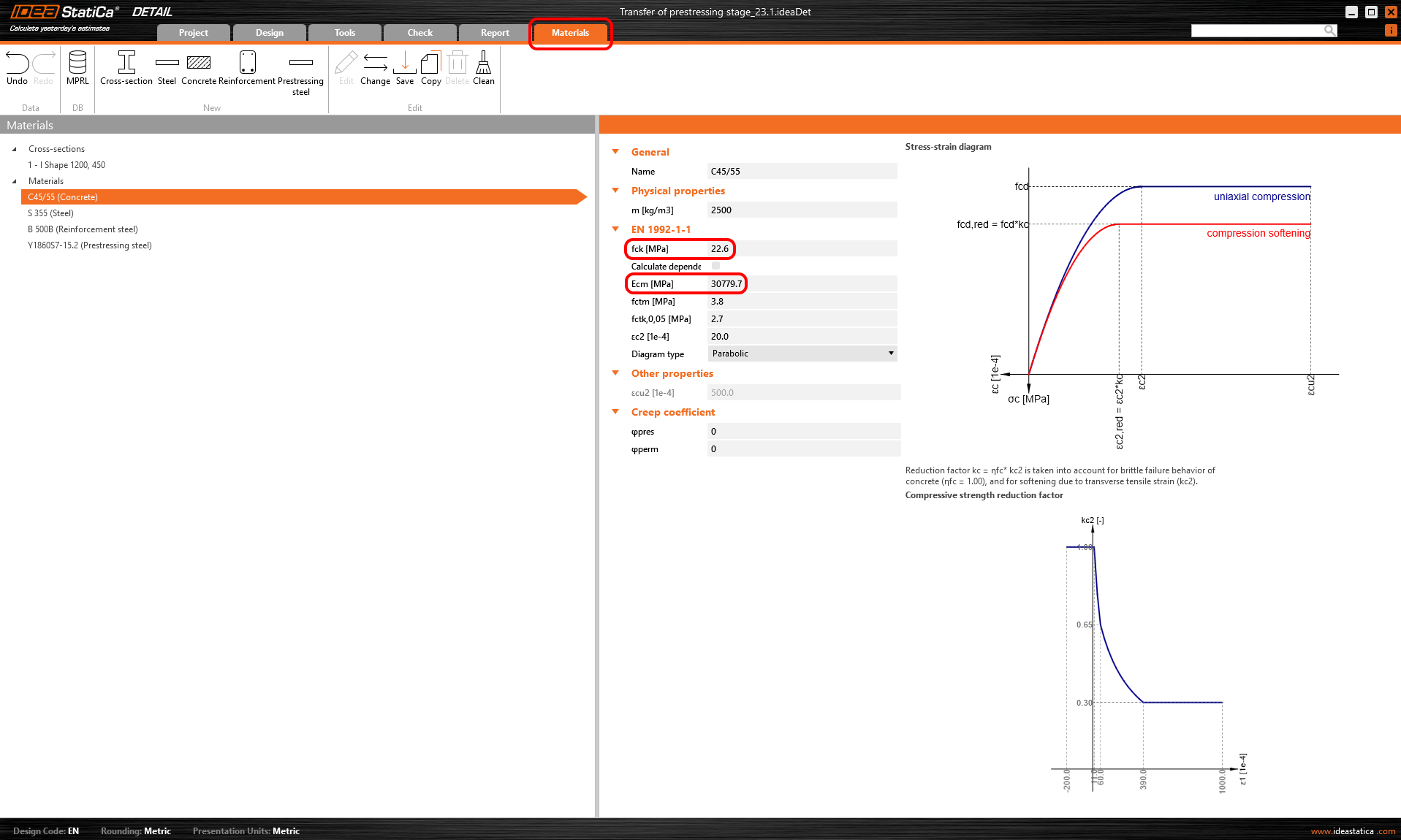
Die Kriechkoeffizienten sind ebenfalls auf Null gesetzt, da wir das Stadium unmittelbar nach der Übertragung der Vorspannung bewerten wollen. Sie können sehen, dass der Wert von Ecm auf denselben Wert umgeschrieben wurde, den wir in Beam eingegeben haben.
Lassen Sie uns also die Ergebnisse vergleichen. Da wir weder einen Kriechfaktor noch einen Langzeitverlust eingegeben haben, sind die lang- und kurzfristigen Auswirkungen die gleichen.
Spannungen in Spanngliedern bei GZG:
Spannung im Beton bei GZG:
- Lesen Sie mehr: Allgemeine Beschreibung der GZG-Ergebnisse in der Detail
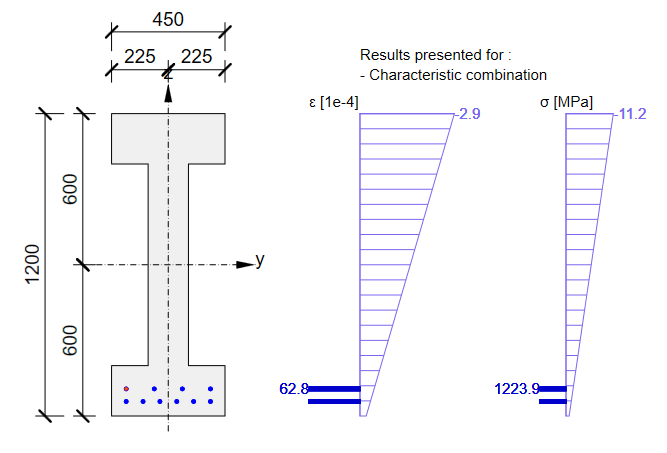
Die GZG-Querschnittsprüfung von Beam:
Wie Sie sehen können, gibt es eine gute Übereinstimmung. Es scheint also, dass wir die Eingaben für diese Phase richtig gemacht haben. Beachten Sie, dass die in EN 1992-1-1; 5.10.9 (1) definierten Koeffizienten rinf und rsup in Beam auf 1,0 gesetzt wurden.
Andererseits ist beim GZT-Nachweis ein signifikanter Unterschied zwischen den Ergebnissen der Beam- und Detail Software zu erwarten. Er wird durch den Verlust aufgrund der unmittelbaren elastischen Betondehnung - Δσpe - verursacht, die in Beam (linearer Ansatz) und in Detail (CSFM) unterschiedlich berechnet wird.
- Beim linearen Ansatz (Beam) ist der Verlust aufgrund der unmittelbaren elastischen Betondehnung Δσpe für GZT und GZG gleich. Der Grund dafür ist, dass wir beim linearen Ansatz das lineare Materialmodell mit dem aus fck berechneten Elastizitätsmodul Ecm für die gesamte Analyse verwenden (auch für die analytische Berechnung der Verluste) und nur für GZT-Querschnittsnachweise das Materialmodell verwenden, bei dem der Elastizitätsmodul aus fcd berechnet wird.
- Beim Ansatz von Detail wird die gesamte GZT mit dem Materialmodell berechnet, bei dem der Elastizitätsmodul aus fcd berechnet wird (auch beeinflusst durch den Faktor ηfc, siehe Materialien). Dies führt zu einer größeren elastischen Dehnung und folglich zu einem größeren Verlust Δσpe. Bitte denken Sie daran, dass wir die Spannung vor dem Verlust aufgrund der unmittelbaren elastischen Betondehnung eingeben. Dieser Verlust wird auf der Grundlage der Dehnung des Modells berechnet, die von den Vorspannkräften beeinflusst wird (im Falle von GZT mit dem niedrigeren Elastizitätsmodul).
Beachten Sie, dass GZG in Detail auf der Grundlage von Ecm (nicht auf der Grundlage von fck) berechnet wird. Andererseits wird GZT auf der Grundlage von fcd berechnet, aus dem das parabolische Spannungs-Dehnungs-Diagramm ermittelt wird.
- Lesen Sie mehr: Allgemeine Beschreibung der GZT-Ergebnisse in Detail
Jetzt wissen Sie, wie Sie Detail für die Bemessung von vorgespannten Betonträgern mit sofortigem Verbund verwenden können. Ändern Sie einfach die Geometrie und fügen Sie einige Diskontinuitäten wie Öffnungen usw. hinzu.
Bemessung mit kurrzeitigen Einflüssen
Die Zeit (Alter des Betons) für diese Phase beträgt 60 Tage. Der Zweck dieser Phase ist die Überprüfung des Betonträgers zu Beginn seiner Nutzungsdauer, einschließlich ständiger und variabler Lasten. Es werden also die beiden anderen Lastfälle hinzugefügt. Die Lastimpulse sind natürlich die gleichen wie im Beam Modell.
Wir müssen zwei Werte als Eingabe für Detail bestimmen.
- Kriechkoeffizient für die Zeit von 2 Tagen bis 60
- Schätzung der Langzeitverluste für den Zeitraum von 2 Tagen bis 60 Tagen
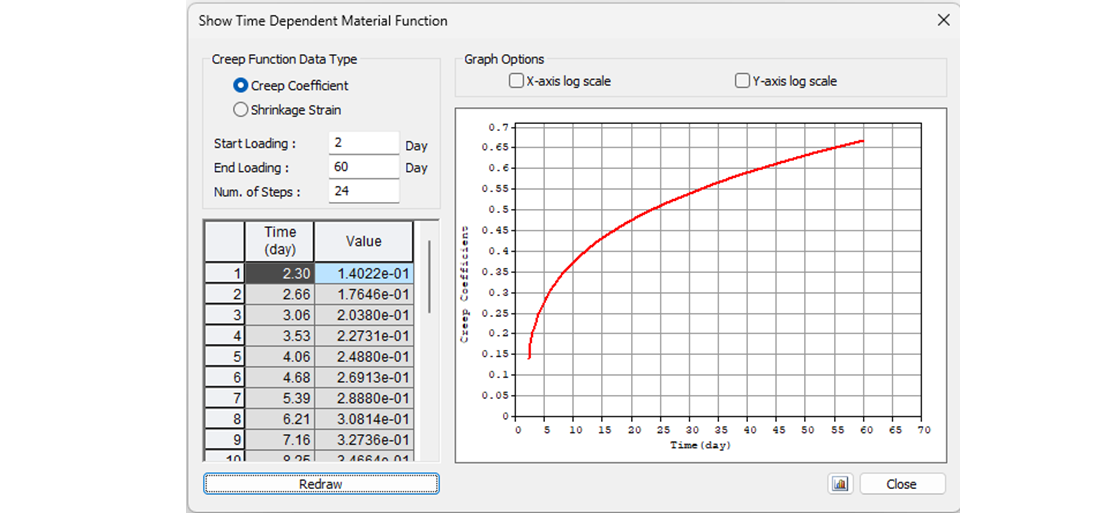
Beginnen wir mit dem Kriechkoeffizienten. In der folgenden Abbildung sehen Sie die Kriechfunktion von 2 bis 60 Tagen für die Betongüte C45/55 und die Zementklasse R nach Eurocode. Der Wert des Kriechkoeffizienten ist dann φpres ≈ φ(60) - φ(2) = 0,65 - 0,15 = 0,50
In Detail kann der Kriechkoeffizient unter Materialien & Modelle eingestellt werden. Es ist offensichtlich, dass der Elastizitätsmodul als Standard-Ecm-Wert eingestellt werden muss (siehe Kapitel " Inkrement" und die dortige Tabelle). Sie werden auch feststellen, dass der Wert von φperm = 0,0 ist, weil wir sowohl ständige Lasten als Kurzzeitlasten und variable Lasten anwenden wollen.
Jetzt ist es Zeit für die langfristigen Verluste. Natürlich können Sie diese schätzen (ich würde sie auf 10 % schätzen). Das ist der einfachste Weg, aber in unserem Beispiel wollen wir es präzise machen. Also haben wir σ60 - Stress nach langfristigen Verlusten in 60 Tagen (blaue Linie) in Beam berechnet, indem wir die Endzeit auf 60 Tage gesetzt haben.
Der Wert von σ60 = 1200 MPa ist aus der folgenden Abbildung ersichtlich (blaue Linie).
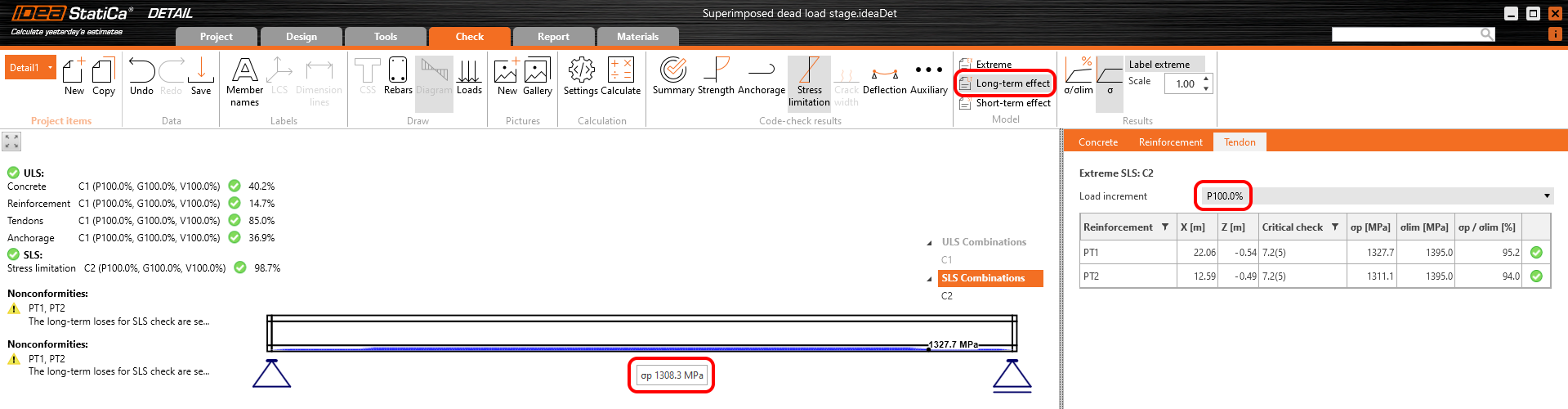
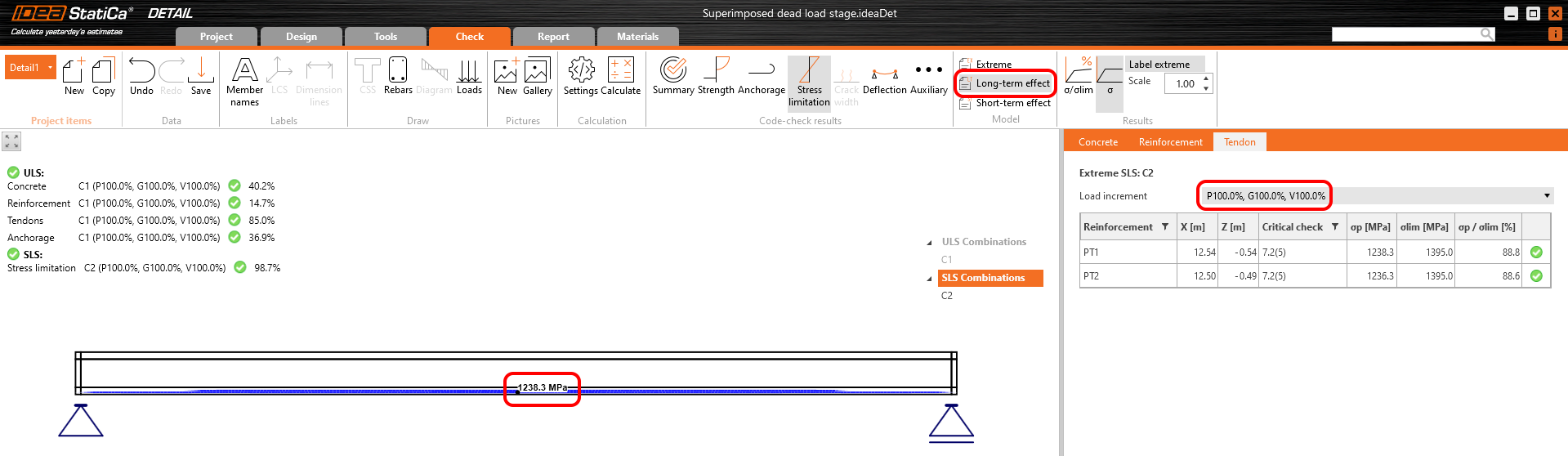
Dann müssen wir das Modell in Detail mit dem eingestellten Kriechkoeffizienten und mit Null Langzeitverlusten für das erste Inkrement - P100% berechnen, um σdet,60 zu bestimmen. Wichtig ist, dass wir die Ergebnisse für die Langzeiteffekte lesen müssen, damit der Kriechkoeffizient berücksichtigt wird.
Aus der Abbildung geht hervor, dass σdet,60 = 1308.5 MPa ist.
Langzeitverluste können dann wie folgt berechnet werden: σ60 / σdet,60 = 1200 / 1308.5 = 0.91 -> Langzeitverlust ist 9%. Geben wir den Wert ein und vergleichen wir die Ergebnisse.
Die Ergebnisse werden für Langzeitverluste (wir wollen Kriechen und Verluste einbeziehen) und für alle Inkremente (wir wollen alle Belastungen einbeziehen) abgelesen.
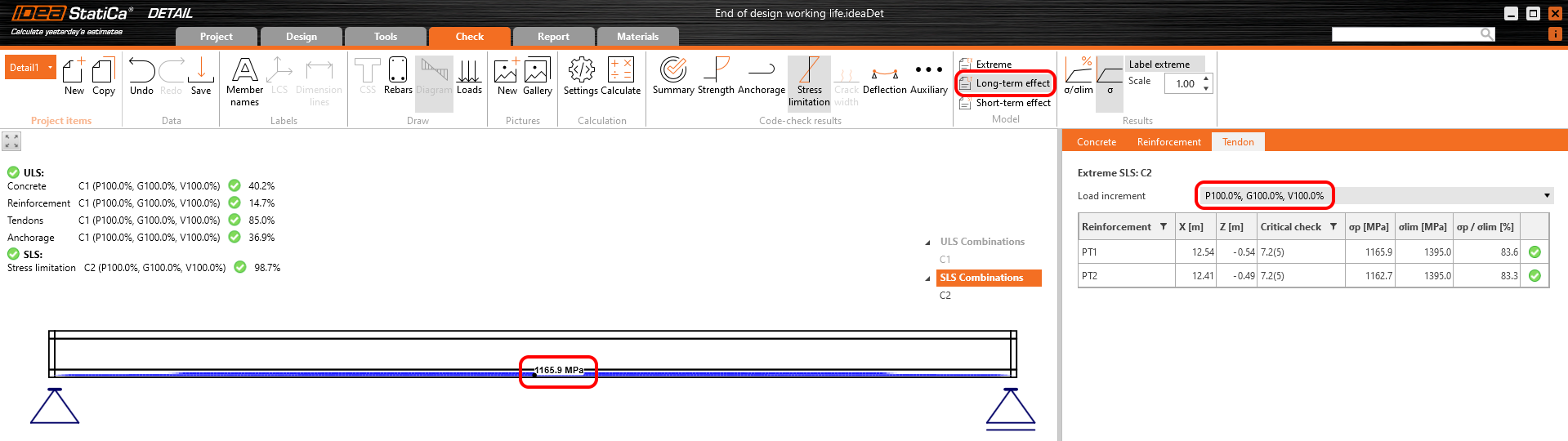
Spannungen in Spanngliedern in GZG:
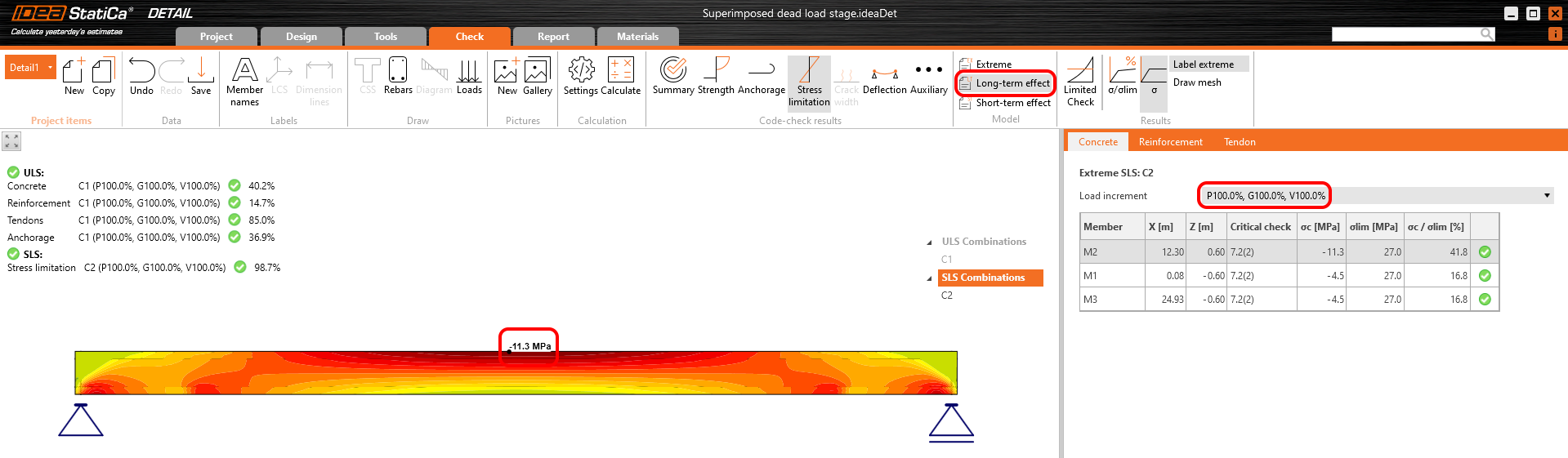
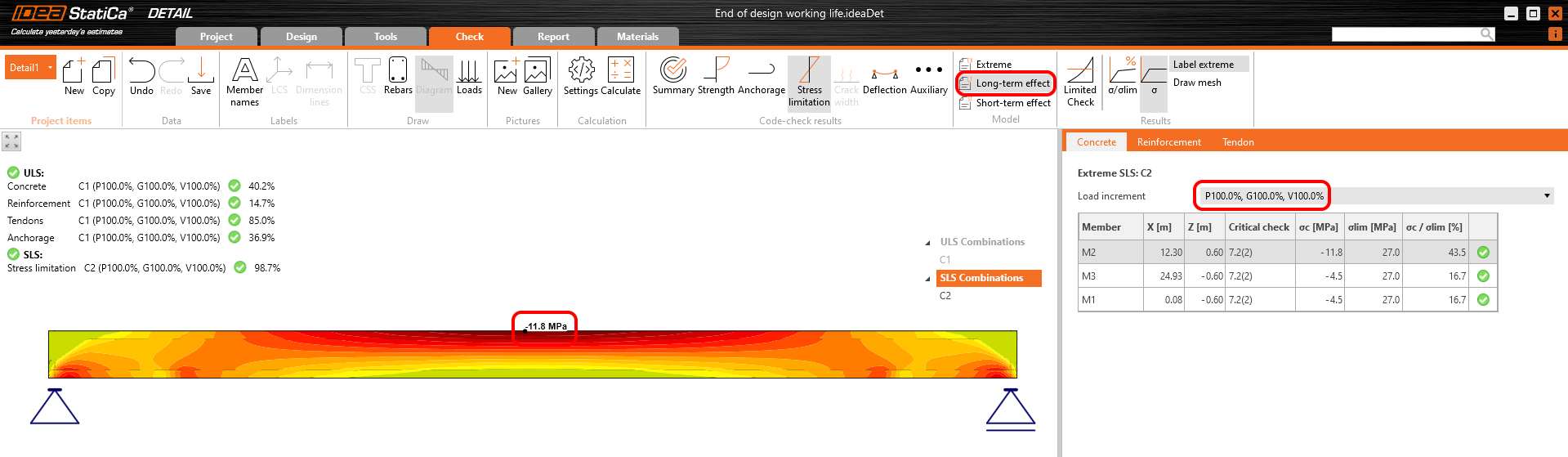
Spannung im Beton bei GZG:
Die GZG-Querschnittsprüfung aus Beam:
Auch hier gibt es eine gute Übereinstimmung. Es sieht also so aus, als hätten wir die Eingaben für diese Stufe richtig gemacht. Für GZT ergibt sich das gleiche Problem wie in der vorherigen Phase beschrieben. Beachten Sie, dass die in EN 1992-1-1; 5.10.9 (1) definierten Koeffizienten rinf und rsup in Beam auf 1,0 gesetzt wurden.
Erinnern Sie sich nun an den Anfang dieses Artikels, wo die Inkremente beschrieben wurden. Im Modell aus Detail für diese Phase können Sie die einzelnen Inkremente durchgehen, um den Einfluss der einzelnen Lastfälle zu sehen. Sie können auch die kurzfristigen Auswirkungen überprüfen, die sich von denen des vorherigen Modells aus Detail für die Phase der Übertragung der Vorspannung unterscheiden werden. Der Grund dafür ist der unterschiedliche Elastizitätsmodul Ecm, der in diesen Modellen verwendet wird.
Ende der Nutzungsdauer des Modells
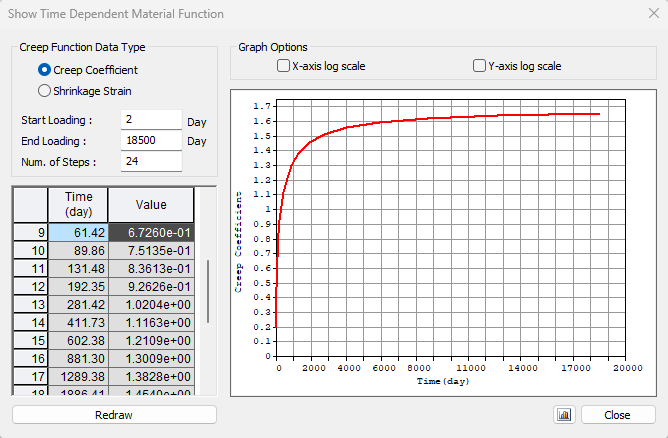
Die Vorgehensweise ist dieselbe wie in der vorherigen Phase. Zunächst müssen wir die Kriechkoeffizienten bestimmen. In der folgenden Abbildung sehen Sie die Funktion des Kriechkoeffizienten.
Der Wert φpres ≈ 1,65 für die Zeit von 2 bis 18250 Tagen für die Zementklasse R nach dem Eurocode. Der Wert φperm = φ(18250) - φ(60) ≈ 1,65 - 0,65 = 1,00 für den Zeitraum von 60 bis 18250 Tagen. Beachten Sie den hervorgehobenen Wert φ(60) in der obigen Tabelle.
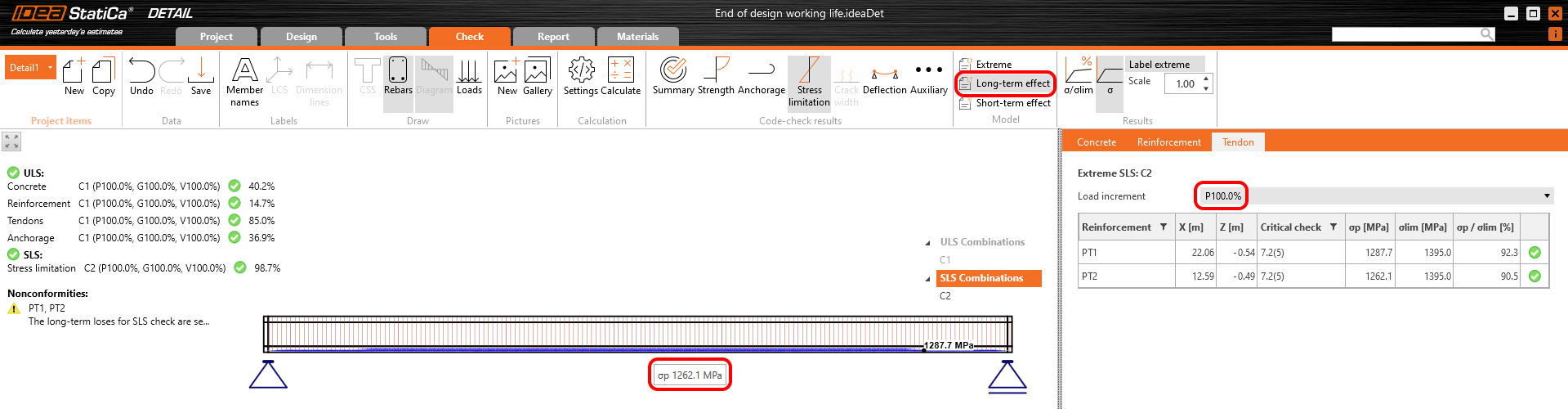
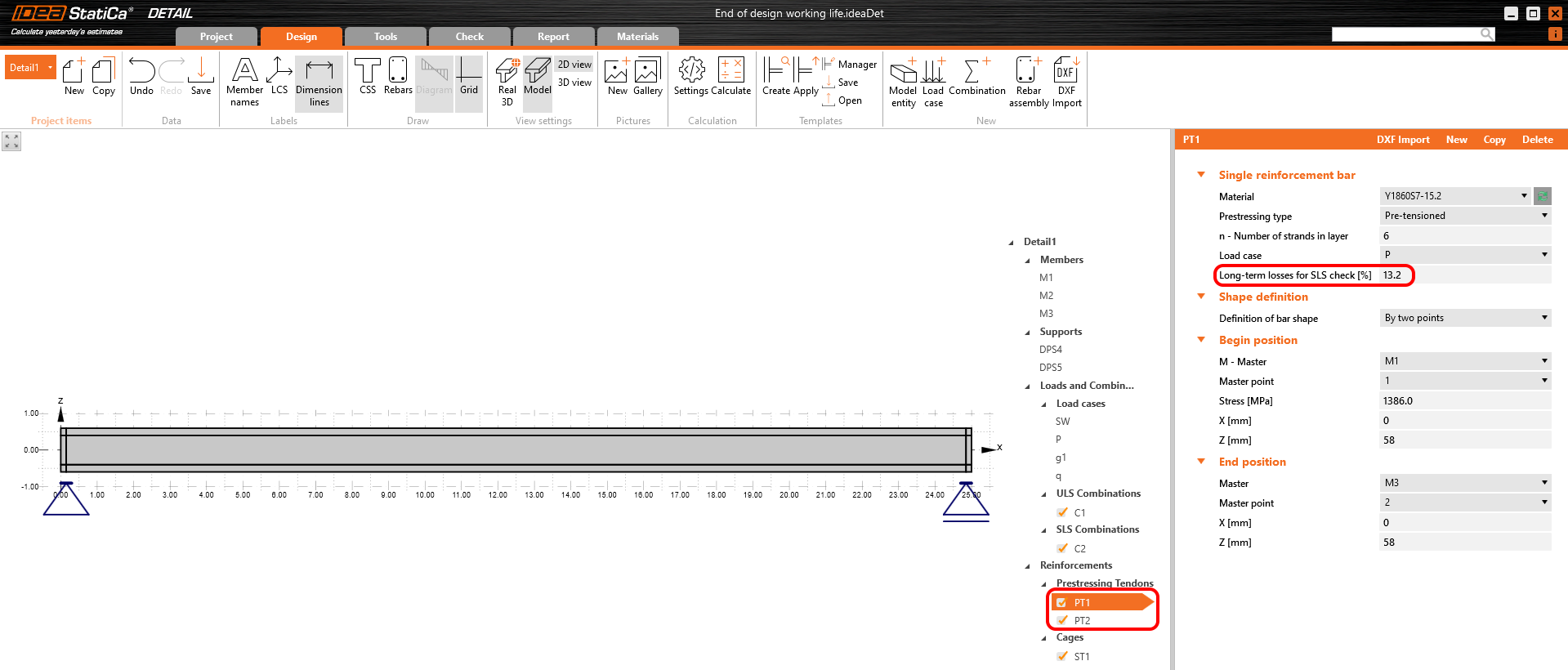
Zweitens brauchen wir die Langzeitverluste. Auch hier haben wir den gleichen Ansatz verwendet, wir haben das Modell in Detail mit den eingestellten Kriechkoeffizienten und mit Null Langzeitverlusten für das erste Inkrement - P100% - berechnet. Wichtig ist, dass wir die Ergebnisse für die Langzeitverluste ablesen müssen, damit der Kriechkoeffizient berücksichtigt werden kann.
Die Langzeitverluste können als σ∞ / σdet,∞ = 1100 / 1267 = 0,868 berechnet werden -> der Langzeitverlust beträgt 13,2 %. Der Wert von σ∞ wird im Kapitel "Die Parameter des Trägers" in der Tabelle "Spannungen/Verluste der Spannglieder" bestimmt. Geben wir den Wert ein und vergleichen wir die Ergebnisse.
Spannungen in Spanngliedern in GZG:
Spannung im Beton bei GZG:
Die GZG-Querschnittsprüfung aus Beam:
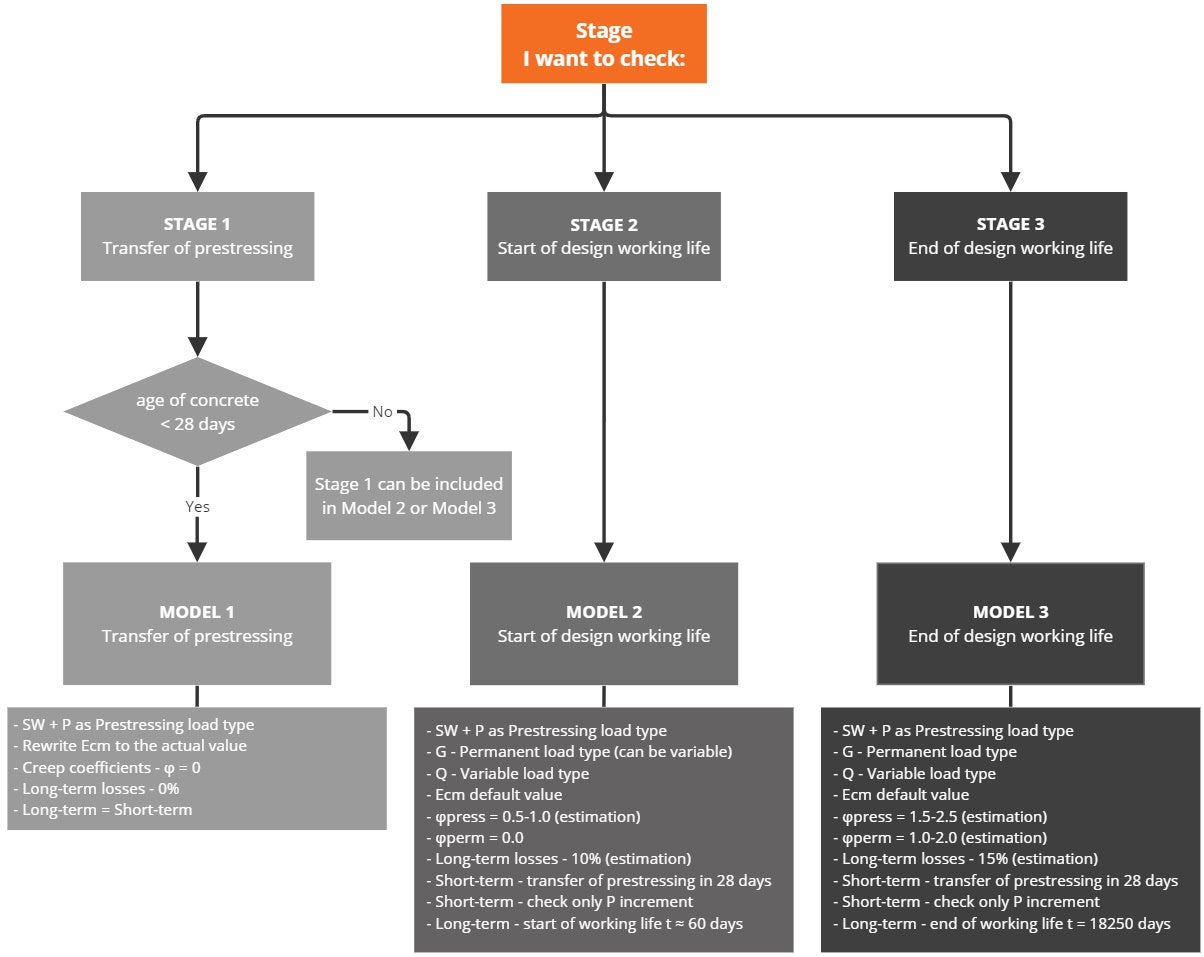
Fazit
Abschließend finden Sie hier einen einfachen Arbeitsablauf, der die oben beschriebene Vorgehensweise bei der Bemessung von Spannbetontragwerken in Detail mit vorgespannten Spanngliedern darstellt.
Es sei nochmals darauf hingewiesen, dass Vorspannung unmittelbar nach dem Lösen (aber vor dem Verlust durch die unmittelbare elastische Betondehnung) eingegeben werden muss. Eine Schätzung der langfristigen Verluste aufgrund von Schrumpfung und Entspannung sollte eingegeben werden. Kriechverluste werden automatisch berechnet.
Daraus folgt, dass bei Modell 2 und Modell 3 für kurzfristige Einwirkungen nur das erste Inkrement P berücksichtigt werden muss (da während des Aufbringens der Vorspannung weder andere ständige Lasten noch variable Lasten aufgebracht werden). Dies gilt nur, wenn das Alter des Betons beim Aufbringen der Vorspannung mehr als 28 Tage beträgt, andernfalls muss ein spezielles Modell für Phase 1 (für kurzfristige Einwirkungen) erstellt werden.
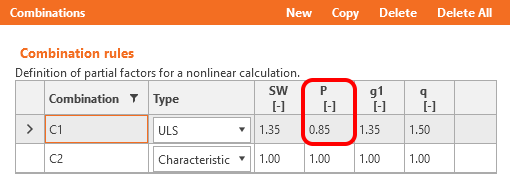
Die Langzeitverluste für GZT müssen als Kombinationsfaktor angesetzt werden. Die Abschätzung der Langzeitverluste, die in der Bewehrung angesetzt werden können, wird nur bei GZG-Nachweisen berücksichtigt. Die Eingabe für die Abschätzung von 15% sollte wie folgt aussehen:
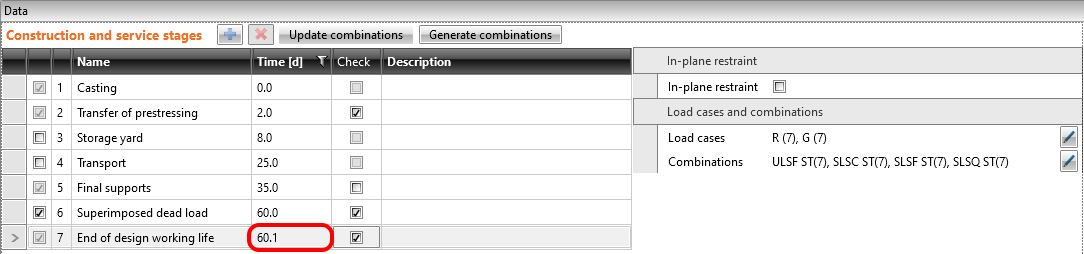
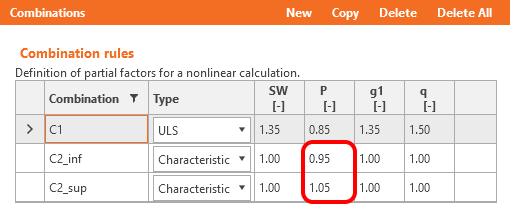
Die in EN 1992-1-1; 5.10.9 (1) definierten Koeffizienten rinf und rsup für Vorspannungseffekte bei GZG sollten auch in Kombinationen berücksichtigt werden. Das bedeutet, dass Sie mindestens zwei Kombinationen erstellen sollten. Siehe die Abbildung.
Lesen Sie mehr über die Implementierung dieser Koeffizienten in Beam in Berücksichtigung der rinf- und rsup-Koeffizienten bei GZG-Nachweisen
Sie haben gelesen, wie man IDEA StatiCa Detail verwendet, eine Betonbemessungssoftware, mit der man unter anderem Spannbetonträger mit Diskontinuitäten bemessen kann. Aber lassen Sie uns nicht IDEA StatiCa Beam vergessen, das für die Bemessung von Betonbalken einschließlich zeitabhängiger Analyse (TDA - Time Depended Analysis) verwendet wird und das wir für den Vergleich der Ergebnisse benutzt haben.
Anhänge zum Download
- BEAM model.ideaBeam (IDEABEAM, 959 kB)
- Transfer of prestressing stage.ideaDet (IDEADET, 13 kB)
- Superimposed dead load stage.ideaDet (IDEADET, 15 kB)
- End of design working life.ideaDet (IDEADET, 15 kB)